Das Sh.P. Statistical Physics of Liquids at Freezing and Beyond
Подождите немного. Документ загружается.

8.1 Mode-coupling theory 391
where the bar denotes an average over the aperiodic distribution of the lattice points {R
i
}.
The similarity of the two expressions (8.1.106) and (8.1.108) for the width parameter α
obtained in the two different pictures is a signature of the link between the corresponding
static and dynamic descriptions. The structure functions h(q) and h
0
(q) corresponding
to the dynamic (MCT) and the static (DFT) description are associated with the uniform
liquid state and the frozen solid state, respectively. Indeed, the frozen lattice structure in
the DFT description of localized density profiles is applicable only over the time scale of
the glassy state during which the underlying lattice {R
i
} remains time-independent. For a
deeper understanding of the two approaches discussed above, a self-consistent treatment
of the problem is necessary.
8.1.6 Dynamic density-functional theory
Our discussion so far involving the mode-coupling models for the dynamics has been for-
mulated in terms of the set of conserved variables consisting of the density ρ and the
momentum density g. A somewhat simpler strategy is to work with a single variable,
namely the fluctuating density ρ. In the supercooled state strong density fluctuations play
the most dominant role in producing the slow dynamics characteristic of these systems.
This is particularly significant since, when the supercooled liquid transforms into a frozen
amorphous state, the freezing starts at short length scales. At short wavelength the energy
and momentum fluctuations in the many-particle system are quickly transferred among the
particles while the individual density fluctuations still decay much more slowly. It is there-
fore plausible that the dynamics for such a system at a somewhat simplified level can be
considered in terms of the density fluctuations only. This has been referred to in the litera-
ture as the dynamic extension of the density-functional theory (DDFT) of freezing which
is used for the study of the freezing transition and was discussed in detail in the earlier
chapters of this book (see Section 6.2.2). The same model equation for the dynamics of
density fluctuations has also been used in studying the kinetics of the freezing transition
into an ordered phase (Munakata, 1978, 1989, 1990; Bagchi, 1987). In the present section
we present the analysis of a hydrodynamic model for which the equation of motion for
the density is given by a nonlinear Langevin equation with a diffusive kernel and multi-
plicative noise (Risken, 1996). As we demonstrate below, this DDFT model also captures
some of the essential properties of the theory formulated in terms of both the mass and the
momentum densities. In particular, this DDFT model also undergoes the ENE transition
discussed above in the context of the fluctuating-hydrodynamics model.
The nonlinear equation of motion
In Section 6.2.2 we obtained the nonlinear Langevin equation for the coarse-grained den-
sity field ρ(x, t) for systems of particles following Newtonian dynamics at microscopic
level. This involved starting from the nonlinear fluctuating-hydrodynamic (NFH) descrip-
tion of classical liquids in terms of {ρ,g} and integrating out the momentum density g from
392 The ergodic–nonergodic transition
the NFH equations with the adiabatic approximation. The final outcome was a single equa-
tion of motion for ρ with multiplicative noise. However, in our earlier discussion of the
nonlinear diffusion equation the multiplicative noise was introduced in an ad-hoc manner.
Subsequently it was demonstrated by Kawasaki and Miyazima (1997) that the same equa-
tion follows in a natural way on using the field-theoretic model for the dynamics in terms
of {ρ,g} and integrating out the momentum variable with the adiabatic approximation. We
now briefly discuss this deduction.
A convenient starting point for this deduction is the Martin–Siggia–Rose action described
in eqn. (7.2.8), including both of the fluctuating variables, density ρ and momentum g.By
integrating out the momentum density field g, the dynamics is formulated in terms of the
density field ρ and its hatted counterpart ˆρ. Let us first consider the equation of motion for
g as given by eqn. (6.2.20) in the form
#
−1
g + f
ρ
= θ, (8.1.110)
where θ is the Gaussian white noise and we have defined
#
−1
= ∂
t
+
0
ρ
−1
≡ ∂
t
+ τ
−1
. (8.1.111)
τ
−1
=
0
/ρ represents a relaxation time scale for the momentum fluctuations. On com-
paring this with eqn. (6.2.20) the force f
ρ
is obtained as
f
ρ
= ρ ∇
δF
U
[ρ]
δρ (r)
. (8.1.112)
The convective nonlinearity term ∇
j
[g
i
g
j
/ρ] in (6.2.20) has been ignored in (8.1.110). F
U
denotes the free energy of the system expressed as a functional of density ρ and determines
the equilibrium state of the liquid, as we discuss further below. F
U
is written as a sum of an
ideal-gas part and an interaction part in the standard Ramakrishnan–Yussouff form given
in eqn. (2.1.38) in terms of the direct correlation form
F
RY
≡ β F
U
=
dx ρ(x)[ln ρ(x) − 1]
−
1
2
dx
1
dx
2
c(x
1
, x
2
;n
l
)δρ(x
1
)δρ(x
2
) +··· (8.1.113)
measured with respect to the free energy of the uniform liquid state at density ρ
0
.The
momentum field g is formally integrated out of the problem by performing a trivial Gaus-
sian integral and the action A[ρ, ˆρ] is written only in terms of the density field ρ and its
hatted conjugate ˆρ.
Let us write the expression (7.2.8) for the action A in the fluctuating-hydrodynamics
formulation involving {ρ, ˆρ, g,
ˆ
g} in the form
A[ρ, ˆρ, g,
ˆ
g]=−
d1
β
4
(#
−1
g + f
ρ
)
−1
0
(#
−1
g + f
ρ
) − i ˆρ( ˙ρ +∇· g)
. (8.1.114)
The quadratic and linear terms in the momentum field g in the first term on the RHS of
(8.1.114) are combined as a perfect square to form a Gaussian integral. The momentum

8.1 Mode-coupling theory 393
field g is then formally integrated out of the problem giving the action in terms of ρ and ˆρ.
Treating the Jacobian as a constant, we obtain
A[ρ, ˆρ]=
d1
1
β
{J · #
0
·
˜
# · J }−βf
ρ
· L
−1
0
· f
ρ
+i ˆρ · ˙ρ
, (8.1.115)
where
˜
# is the adjoint of # and the current J is now expressed as
J = β
˜
#
−1
L
−1
0
f
ρ
−i ∇ˆρ. (8.1.116)
The complicated result of (8.1.115) is simplified by making some rather strong assump-
tions. In the so-called adiabatic approximation the momentum density is assumed to relax
very fast so that the operator #
−1
can be replaced by
0
ρ
−1
≡ τ
−1
. The action (8.1.115)
is simplified to the form
A[ρ, ˆρ]=−
d1
τ
β
ρ(∇ˆρ)
2
+i ˆρ{− ˙ρ +τ ∇· f
ρ
}
. (8.1.117)
The action functional given by (8.1.117) reduces to a convenient form with the identifica-
tion of the bare transport coefficient D
0
= τ/β (with the particle mass taken to be unity).
Using the transformation ˆρ → D
−1
0
ˆρ, we obtain for the MSR action
A[ρ, ˆρ]=−
d1
D
−1
0
ρ(∇ˆρ)
2
+i ˆρ
#
−D
−1
0
˙ρ + β∇ · f
ρ
$
(8.1.118)
as a functional of ρ and ˆρ.OntheRHSofeqn. (8.1.118) we denote a space-time integral
over variables r and t simply as d1 and the arguments (r, t ) for different functions are
dropped for the sake of brevity. This form of the action (8.1.118) conforms to the following
stochastic Langevin equation for the density field:
∂ρ
∂t
= D
0
∇ ·
ρ ∇
δF
U
δρ
+
√
ρθ, (8.1.119)
where we have multiplicative noise. The correlation of the noise θ is
1
θ(x, t)θ(x
, t
)
2
= 2D
0
δ(t − t
)∇
x
∇
x
{δ(x − x
)}. (8.1.120)
The FNH description in terms of the additive noise is thus reduced to the DDFT model
equation with multiplicative noise and without the 1/ρ nonlinearities in the equations of
motion.
F
U
is a functional of the density field ρ that controls the equilibrium state of the fluid
(see below) and is often identified with the Ramakrishnan and Yussouff (1979) free-energy
functional introduced in the equilibrium density-functional theories discussed in Chapter 2.
The functional
2
F is expressed as a sum of an ideal-gas part F
id
and an interaction contri-
bution in terms of the direct correlation functions c
(n)
:
F = F
id
[ρ]+F
in
[ρ], (8.1.121)
2
From now on we drop the subscript in F
U
etc. and simply write it as F ≡ F[ρ], understood to be a functional of the density ρ.
394 The ergodic–nonergodic transition
where
β F
id
[ρ]=
dx ρ(x)[ln
#
3
0
ρ(x)
$
− 1], (8.1.122)
β F
in
[ρ]=−
∞
n=1
1
n!
dx
1
... dx
n
c
(n)
(x
1
,...,x
n
)δρ(x
1
)...δρ(x
n
), (8.1.123)
where
0
is the thermal de Broglie wavelength and δρ denotes the fluctuation of density
around the density of a uniform liquid state. Using this general expression for the free-
energy functional in eqn. (8.1.119), we obtain the corresponding equation of motion for
the density field,
∂ρ
∂t
= D
0
∇
2
ρ − D
0
∇ρ(x, t) ∇
dx
v
eff
(x − x
)ρ(x
, t), (8.1.124)
v
eff
(x − x
) =
∞
n=2
1
(n − 1)!
dx
3
... dx
n
× c
(n)
(x, x
, x
3
,...,x
n
)δρ(x
3
)...δρ(x
n
). (8.1.125)
This is generally termed the Vlasov–Smoluchowski equation (Smoluchowski, 1915) and
has been used for studying the dynamics of density fluctuations in different systems (Calef
and Wolynes, 1983; Munakata, 1978, 1989; Bagchi, 1987). If the free-energy expansion is
formally truncated at the two-point level, we obtain v
eff
(x − x
) = c
(2)
(x − x
).
Equation (8.1.119) for the coarse-grained density ρ(x, t ) is identical in form to the exact
balance eqn. (6.3.14) for the microscopic density
3
˜ρ(x, t) for a system of particles with
Brownian dynamics (BD). For this, see the deduction of eqn. (6.3.14) in Section 6.3.1.This
similarity also requires identifying the Ornstein–Zernike two-point direct correlation func-
tions c(r) appearing in the Kawasaki equation of motion (8.1.119) for the coarse-grained
density ρ with the bare interaction potential βU (r) in the corresponding exact balance
equation of Dean for the microscopic density ˜ρ. Even though it is often presented as the
Dean–Kawasaki model, the corresponding densities involved are different. The balance
equation is for ˜ρ(x, t), which is not the coarse-grained density ρ(x, t).
The Fokker–Planck description
The DDFT model for the fluid in terms of the density ρ(x) is alternatively described
with the corresponding probability density functional P[ρ,t]. The time evolution of P
is given by the corresponding Fokker–Planck equation. We obtained earlier eqn. (6.1.63)
for the time evolution of the probability distribution of a set of fields {φ
i
} with the cor-
responding Fokker–Planck operator D
φ
being given by eqn. (6.1.61). In the present case
the bare transport operator is of the form L
0
ij
≡∇
i
ρ∇
i
and the reversible current V
i
[φ] is
3
Here we call the microscopic density ˜ρ, instead of ˆρ as was done in Section 6.3.1, to avoid confusion with the MSR conjugate
field to
ρ(x, t).

8.1 Mode-coupling theory 395
zero. Hence the Fokker–Planck equation for the time evolution of the probability P[ρ] is
obtained as
∂
∂t
P[ρ,t]=−D
ρ
P[ρ,t], (8.1.126)
where the operator D
ρ
is given by
D
ρ
= D
0
dr
δ
δρ (r)
∇ · ρ(r)∇
k
B
T
δ
δρ (r)
+
δF[ρ]
δρ (r)
. (8.1.127)
The positive constant D
0
is treated as a bare transport coefficient. The stationary solution
of (8.1.127) is given by exp[−β F] and therefore F is termed the free-energy functional
in terms of the density function. F has the same form as is used in the density-functional
models discussed in Chapter 3. The above Fokker–Planck equation for the dynamics of the
density distribution is obtained (Kawasaki, 1994) from the Smoluchowski (1915) equation
for interacting colloidal particles without hydrodynamic interactions through a suitable
coarse-graining procedure.
The H -theorem
It is possible to reach a suitable H-theorem in the present problem (Munakata, 1994)of
density fluctuations. First, we consider the deterministic form of the dynamic equation,
ignoring the noise in eqn. (8.1.119). The rate of change of the free energy is obtained as
dF
dt
=
dx
δF
δρ (x, t)
∂ρ(x, t)
∂t
=−β D
0
dx
δF[ρ]
δρ (x, t)
2
ρ(x, t) ≤ 0, (8.1.128)
since the density ρ(x, t) is always positive. F reaches a minimum when the functional
derivative of F[ρ] with respect to density is a constant, i.e.,
δF
δρ (x, t)
= μ, (8.1.129)
where μ is a chemical potential.
Next we consider the equation of motion (8.1.119) including the random part. The
corresponding H function is obtained as
H
ρ
[P]=
Dρ{F[ρ]P[ρ,t ]+k
B
TP[ρ,t]lnP[ρ,t]}. (8.1.130)
The time rate of variation of H
ρ
is given by
dH
ρ
[P]
dt
=
Dρ[F[ρ]+k
B
T ln P[ρ,t]]
∂ P[ρ,t]
∂t
+ k
B
T
d
dt
Dρ P[ρ,t]. (8.1.131)
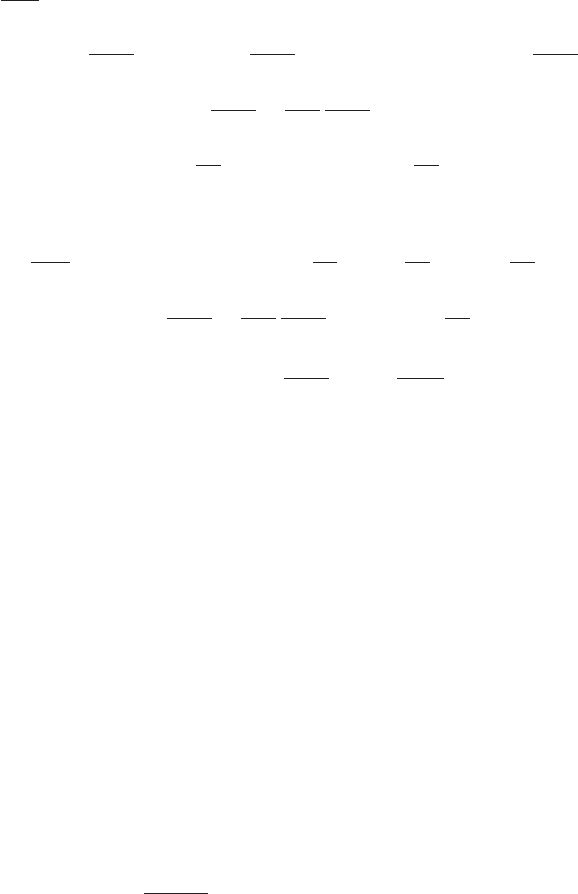
396 The ergodic–nonergodic transition
The last term vanishes due to conservation of probability P[ρ,t]. Using the Fokker–Planck
eqns. (8.1.126) and (8.1.127), we obtain the result,
dH
ρ
dt
=−D
0
Dρ
dx
F[ρ]+k
B
T ln P[ρ,t]
×
δ
δρ (x)
3
∇ · ρ(x)∇
δF
δρ (x)
4
P[ρ,t]+k
B
T
3
∇ · ρ(x)∇
δ P
δρ (x)
4
= D
0
Dρ
dx
δF
δρ (x)
+
k
B
T
P
δ P
δρ (x)
×
3
∇ · ρ(x)∇
δF
δρ
4
P + k
B
T
3
∇
i
ρ(x)∇
i
δ P
δρ
4
. (8.1.132)
The RHS is further simplified by doing a partial integration w.r.t. x to obtain
dH
ρ
dt
=−D
0
Dρ
dx
∇
i
P
δF
δρ
+ k
B
T
δ P
δρ
3
ρ∇
i
δF
δρ
4
+
∇
i
δF
δρ (x)
+
k
B
T
P
δ P
δρ (x)
k
B
T
3
ρ∇
i
δ P
δρ
4
=−D
0
Dρ
dx
3
∇
δF
δρ (x)
+ k
B
T
δ ln P
δρ (x)
4
2
P[ρ,t]ρ(x)
≤ 0, (8.1.133)
since both ρ and P are always positive. Therefore the generalized H function always
decreases. The RHS of eqn. (8.1.132) is zero for the stationary distribution
P
eq
∼ exp
−β
3
F[ρ]−μ
dx ρ(x)
4
, (8.1.134)
where μ is the chemical potential for the equilibrium state. The random part of the equation
of motion (8.1.119) therefore drives the system to its lowest free-energy minimum. Next we
focus on the relevance of the DDFT model described by the nonlinear diffusion equation
(8.1.119) for the coarse-grained density ρ with respect to the ENE transition discussed
above.
Renormalization
Let us now consider the nature of the dynamics resulting from the nonlinear stochastic
equation for density obtained in the previous section. If we ignore the interaction between
the particles and replace the free-energy functional by the ideal part F
id
given by eqn.
(6.3.17), then eqn. (6.3.14) represents simple diffusion:
∂ρ(x, t)
∂t
= D
0
∇
2
ρ(x, t) + ρ
1/2
0
θ(x, t). (8.1.135)
The correlation of the noise θ is given by (6.3.13), with the density ρ being replaced with ρ
0
at the linear level. For the linear dynamics the correlation functions are straightforward to
compute in the MSR formalism in terms of ρ and the corresponding hatted field ˆρ.Forthe

8.1 Mode-coupling theory 397
density ρ variable we define the correlation functions in terms of the density fluctuations,
i.e., ρ = ρ
0
+ δρ. The frequency and wave-number transform of the zeroth-order matrix
G
−1
0
is obtained from the action given in (8.1.118),
G
−1
0
(q,ω) =
⎡
⎢
⎢
⎢
⎣
ρ ˆρ
0 ωD
−1
0
−iq
2
ρ
ωD
−1
0
+iq
2
α
0
D
−1
0
q
2
ˆρ
⎤
⎥
⎥
⎥
⎦
, (8.1.136)
where we denote α
0
=2β
−1
ρ
0
.
Let us consider the implications of the nonlinearities in the equations of motion involv-
ing coupling of density fluctuations. For this, we obtain the full matrix G
−1
of two-point
correlation functions. This matrix is a generalization of the Gaussian matrix G
−1
0
and is
computed in terms of the corresponding self-energy matrix using the Schwinger–Dyson
equation (7.1.27). The renormalizability of the theory here will imply that the correlation
function G
−1
in the nonlinear theory maintains the form of the matrix (8.1.136) in which
the transport coefficient D
0
is replaced with the renormalized quantity D
R
. The bare trans-
port coefficient D
−1
0
is corrected either from the self-energy
ˆρ ˆρ
or from the response
self-energy
ˆρρ
, in the correlation and response parts of the G
−1
matrix, respectively. A
consistent form of the renormalized theory is obtained if we assume that the two types of
self-energies are related through a fluctuation–dissipation theorem
2β
−1
ρ
0
ˆρρ
(ω) =
ω
q
2
ˆρ ˆρ
(ω) =−
ρ ˆρ
(ω)
∗
. (8.1.137)
Upon inverting the full correlation function matrix G
−1
(q,ω), we obtain for the normal-
ized density correlation function
ψ(q, z) =
1
z + i
2
q
/D
−1
R
(q, z)
. (8.1.138)
By evaluating the self-energies up to one-loop order we obtain the generalized diffusion
coefficient D
R
for the renormalization of D
−1
0
as (Kawasaki and Miyazima, 1997)
D
−1
R
(q,ω) = D
−1
0
+
dk
(2π)
3
˜
V
q,k
G
ρρ
(k, t)G
ρρ
(q − k, t). (8.1.139)
To understand the above one-loop correction term, we note that, in the notation of (7.3.56),
the crucial vertex function V
ˆρρρ
[q, q − k] represents the coupling of the density fluctu-
ations. It gives rise to a cubic nonlinearity in the non-Gaussian part of the action and
is in fact identical to the vertex function V
L
(q, k) defined in (8.1.34) in the fluctuating-
hydrodynamics model. The vertex function
˜
V
q,k
is obtained as
˜
V
q,k
=
S(q)
2ρ
0
q
2
!
(
ˆ
q · k)c(k) +
ˆ
q ·(q − k)c(|q − k|)
"
2
, (8.1.140)
in terms of the two-point Ornstein–Zernike direct correlation function c(r) which defines
the interaction part of F in eqn. (8.1.113).

398 The ergodic–nonergodic transition
The dynamic transition is characterized by the point at which the density correlation
function develops a 1/z pole as D
−1
R
diverges for small z. The asymptotic behavior of the
density correlation function as predicted by the eqns. (8.1.138) and (8.1.139) is identical to
what we obtained with the mode-coupling model involving {ρ,g}. To demonstrate this, we
consider the nonergodicity parameter f
q
as the long-time limit of the normalized density
correlation function,
lim
t→∞
G
ρρ
(q, t)
S
ρρ
(q)
≡ f
q
. (8.1.141)
On taking the long-time limit of eqns. (8.1.138) and (8.1.139), we obtain that the f
q
satisfy
the integral equation
f
q
1 − f
q
=˜m(q, t →∞), (8.1.142)
where the kernel ˜m(q, t) at one-loop order is given by
˜m(q, t) =
1
2ρ
0
β
dk
(2π)
3
˜
V
q,k
S(k)S(k
1
) f
k
1
f
k
. (8.1.143)
The integral equations (8.1.142) for the nonergodicity parameters in the DK model are
the same as the corresponding eqns. (8.1.36) in the FNH model. The detailed wave-vector
dependences of the vertex functions are identical to one-loop level in the two models as
described in eqns. (7.3.67) and (8.1.140). This implies that the DDFT model undergoes
an identical ergodic–nonergodic transition. However, in the case of DDFT the effect of the
mode coupling now appears in the form of a lifetime renormalization. The model described
above is primarily based on the assumption that the full correlation function G (with all
nonlinearities taken into account) is expressed in a form (involving renormalized transport
coefficients) similar to that of G
0
, i.e., the assumption is that the theory is renormaliz-
able in terms of a generalized diffusion coefficient D
R
(q, z). The assumed FDT relation
(8.1.137) is ad hoc. It is easy to see that this relation holds if we consider the one-loop dia-
gram for the respective self energies (similar to Fig. 7.1) and evaluate the graphs with the
zeroth-order Green function G
0
. In other words, the FDT holds at O(k
B
T ) in a non-self-
consistent calculation. The construction of the self-consistent renormalized model (for the
ergodic–nonergodic transition) with all the associated nonlinearities is intricate but keeps
the basic result unchanged at the lowest order (Kim and Kawasaki, 2008). We present this
in Appendix A8.2.
At a somewhat more general level the equation of motion (8.1.119) for the density
function ρ(x, t) has often been considered in a form with a density-dependent transport
coefficient D(ρ):
∂ρ(x, t)
∂t
=∇
i
D(ρ)∇
i
δF
δρ (x, t)
+ η(x, t). (8.1.144)

8.1 Mode-coupling theory 399
The noise η in the Langevin equation obtained above is multiplicative and its correlation is
given by
1
η(x, t)η(x
, t
)
2
= 2k
B
T δ(t − t
)∇
x
∇
x
{D(ρ)δ(x − x
)}. (8.1.145)
The free-energy functional F in eqn. (8.1.144) is simply written as a functional of density
ρ(x). The DDFT model is a particular case with D(ρ) ≡ ρ so that the bare diffusion
coefficient is linear in density. Another variant of this model is the hindered-diffusion or
random-diffusion model (RDM), in which the driving free energy is chosen to be purely
quadratic (Gaussian) (Mazenko, 2008),
F[ρ]=
1
2
dx
1
dx
2
δρ (x
1
)χ
−1
(x
1
− x
2
)δρ(x
2
), (8.1.146)
making the static behavior trivial. However, a high-density constraint is imposed on the
bare diffusion coefficient with the following choice for D(ρ):
D(ρ) = D
0
ρ
c
− ρ
ρ
c
θ(ρ
c
− ρ), (8.1.147)
where D
0
is the diffusion constant in the low-density limit and ρ
c
is a positive param-
eter in the theory. This is a departure from the usual approach of nonlinear fluctuating
hydrodynamics, in which bare transport coefficients are treated as constants. This model
is analogous to the facilitated-spin models (Fredrickson and Andersen, 1984; Garrahan
and Chandler, 2002, 2003; Whitelam et al., 2005), in which kinetic coefficients depend on
the local environment in a lattice. In the continuum limit with the conserved density the
corresponding diffusion coefficient is density-dependent in the RDM.
The self-consistent renormalized perturbation theory has been worked out to two-loop
order in the RDM. This treatment goes beyond that of the above models, which are gen-
erally treated to one-loop order. There are two ways of analyzing this perturbation-theory
result for the RDM, giving rise to an interesting situation. Using the Kawasaki rearrange-
ment described in appendix A8.2, at one-loop order, the mode-coupling theory with an
ergodic–nonergodic transition is obtained. However, at two-loop order it has been shown
that the ergodic–nonergodic transition is not supported. This is possibly indicating that
ENE transition of the DDFT model might not be viable at higher orders. It has further
been demonstrated in the RDM that the corresponding mode-coupling theory gives rise
to a growing length scale (Mazenko, 2008; McCowan and Mazenko, 2010). The dynamic
density correlation function computed in this theory at one-loop order leads to a slowing
down as the relevant nonlinear coupling increases. Eventually one hits a critical coupling at
which the time decay becomes algebraic. Near this critical coupling a weak peak develops
at a wave number well above the zero-wave-number peak associated with the conservation
law. The width of this pre-peak in Fourier space decreases with time and can be identified
with a characteristic kinetic length that grows with a power law in time. The new peaked
state is maintained at two-loop order.
400 The ergodic–nonergodic transition
8.2 Evidence from experiments
For the supercooled liquids, MCT now plays the role which van der Waals theory did for
the theories of phase transition at the mean-field level. The theory offers a microscopic
model for the dynamics of supercooled liquids in the initial stages of viscous slow-down.
With the development of better experimental tools and fast computers, it has now become
possible to probe the liquid-state dynamics over a wide range of time scales, ranging up
to 18 decades. This has revealed a rich set of hitherto unknown features of the dynamics
of the supercooled state. It is here that a microscopic theory like MCT has provided the
clue to understanding the experimental (laboratory or computer) observations. The main
achievement of MCT has been that, starting from a statistical-mechanical approach, the
existence of a crossover temperature T
c
that is greater than the calorimetric glass-transition
temperature T
g
has been identified in the supercooled liquid. T
c
signifies a dynamic tran-
sition in the liquid, and, in its close vicinity, interesting scaling behavior is predicted
over varying length and time scales. In the present section we briefly review the predic-
tions of the MCT that have been put to the test through detailed analysis of data from
experiments.
The experimental techniques used in such studies include neutron- and light-scattering
methods, dielectric spectroscopy, and measurements of the mechanical response of the
supercooled liquid to external perturbations. In making such comparisons, it is generally
assumed that correlations of other variables such as, for example, the dielectric moment,
couple to the density, both obeying the same type of relaxation law. These comparisons
with experimental data, barring a few exceptions, are mainly done w.r.t. the predictions of
the above-described idealized model which involves a sharp transition of the supercooled
liquid to a nonergodic glassy state.
8.2.1 Testing with schematic MCT
For comparing the scattering data from experiments, often the schematic theoretical model
without wave-vector dependence (described in the schematic model of the previous sec-
tion) is chosen. In most cases the data analysis is done by treating the relevant quantities
(such as the NEP f , and the exponent parameter λ) appearing in the MCT as fitting param-
eters. Also it is generally assumed that the role of the ergodicity-restoring mechanisms is
minimal, at least over the time scale of the specific effect being studied.
The nonergodicity parameter
The cusp behavior of the nonergodicity parameters (NEPs) indicated in eqn. (8.1.46) is an
asymptotic result and is valid only in the close vicinity of the transition point. The tem-
perature dependences of the NEPs f
q
and f
s
q
, corresponding to the long-time limit of the
density and tagged-particle correlations, respectively, have been studied by a number of
workers (Frick et al., 1990; Li et al., 1993) in order to locate the mode-coupling tran-
sition point T
c
indirectly. Theoretically the NEP is the weight of the contribution by the
