Даниленко Т.С. Организация и производство геодезических работ при крупном строительстве

Подождите немного. Документ загружается.

3. Для текущего повседневного геодезического обслуживания

строительных работ целесообразно перевычислить координаты пунк-

тов геодезической опорной сети в систему проектной разбивочной

сетки (рис. 67, в), пользуясь правилами перевычисления координат

из одной системы в другую.

Например, положение точки К определится пересечением ство-

ров АС и BD. Координаты (в системе разбивочных осей сооруже-

ний) точки К можно вычислить по формулам (VI. 12). Получим

= 454,61; у

= 490,90.

Оценку точности координат точки К можно произвести по

формулам (VI. 17).

§ 51. ОПРЕДЕЛЕНИЕ ВЕСОВЫХ КОЭФФИЦИЕНТОВ

ГЕОДЕЗИЧЕСКОГО ЧЕТЫРЕХУГОЛЬНИКА

В сети из одного самостоятельного геодезического четырех-

угольника (рис. 68) примем пункты А, В за твердые, а пункты С,

D — за определяемые.

Величины средних квадратических ошибок абсцисс или ординат

определяемых пунктов в сети зависят от ее

ориентирования, но средняя квадратическая

ошибка положения пункта не зависит от на-

правления осей координат.

Для оценки точности элементов сети три-

ангуляции воспользуемся весовыми коэффици-

ентами.

Результаты наблюдений в сети могут быть

уравнены параметрическим способом.

Неизвестными будут поправки в коорди-

наты пунктов С и D, т. е. Ьхс, 8Ус, &x

, by

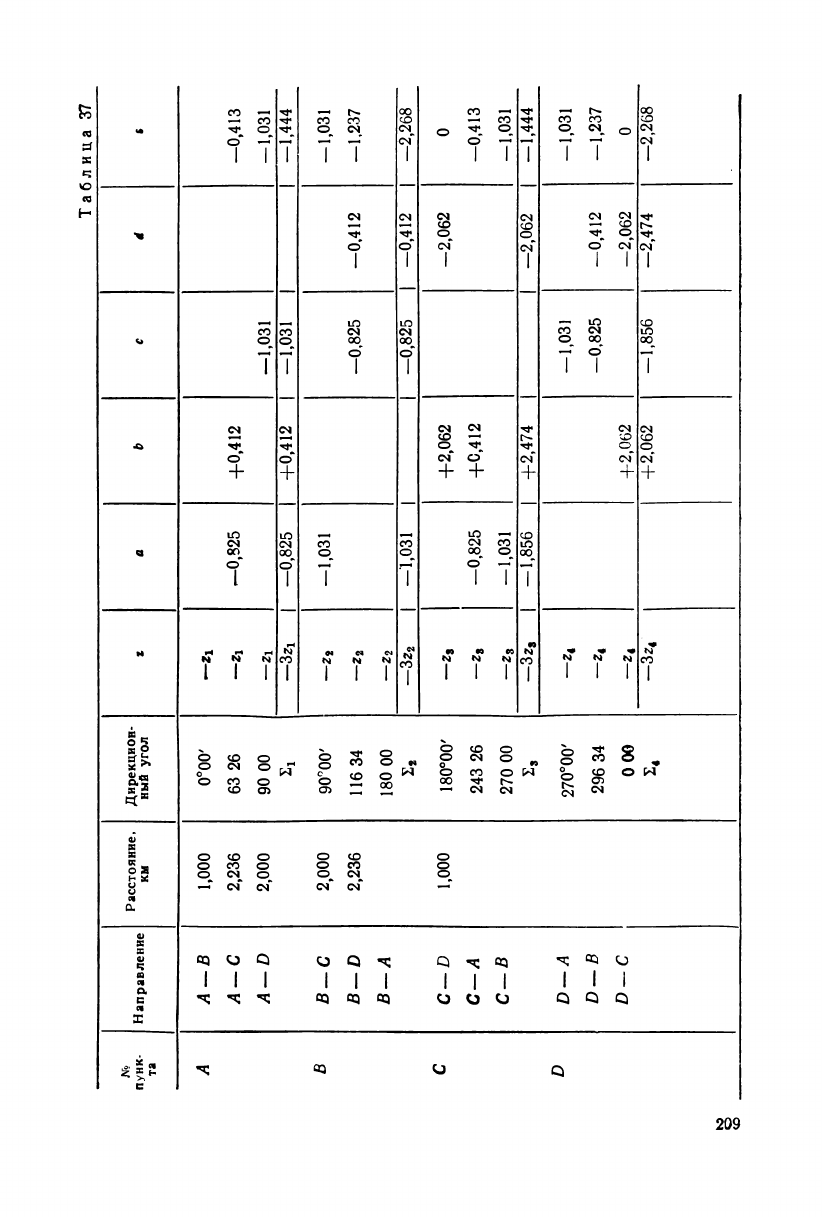
Уравнения ошибок составим согласно

(IV.60) для прямоугольного геодезического

четырехугольника двойной вытянутости (табл.

37), причем свободные члены, как не имеющие значения при оты-

скании весовых коэффициентов, отбросим.

По данным табл. 37, пользуясь формулами (IV.61)—(IV.65),

найдем коэффициенты при неизвестных нормальных уравнений,

которые выписаны в строках N

табл. 38.

Веса двух последних неизвестных при решении нормальных

уравнений вычисляют по способу Энке, основанному на использо-

вании преобразованных коэффициентов [И], [92]. При четырех

нормальных уравнениях обратный вес последнего неизвестного

составляет

Рис. 68. Свободный

геодезический четы-

рехугольник

208

1 ! О

(VI.25)

Таблица

№

пунк-

та

Направление

Расстояние,

км

Дирекцион-

ный

угол

а ь

А—В

1,000

0°00'

А —С

2,236

63 26

—Zi

^0,825

+0,412

—0,413

А — D

2,000

90 00

—2i

—1,031

— 1,031

—3zi

—0,825

+0,412

— 1,031

— 1,444

В-С

2,000

90°00'

—2

—1,031

-1,031

В — D

2,236

11634

—0,825 —0,412

— 1,237

В-А

180 00

—2

—32

—1,031 —0,825

—0,412 —2,268

—

1,000

180°00

—2з

+2,062

—2,062

С — А

243 26

—2

—0,825

+0,412

-0,413

с-в

270 00

—2

— 1,031

-1,031

-32з |

—1,856

+2,474 —2,062

— 1,444

D — A

270°00'

—2

— 1,031

-1,031

D — B

296 34

—2

—0,825 -0,412

— 1,237

D — С

ООО

—2

+2,062

—2,062

—32

+2,062

— 1,856

—2,474

—2,268

а вес предпоследнего неизвестного

р _ ^зз

где

(VI.26)

Таблица 38

Обозначения

строк

"и

+ 1,758

+0,965

—0,54892

—0,566

+0,32196

— 1,418

+0,80660

+0,719

+5,329

+4,7993

+ 1,418

+ 1,7287

—0,36020

—5,104

—4,3262

+0,90142

+2,608

д;

(2)

N31

+ 1,758

+0,9531

—0,965

+0,1368

—1,14353

+ 1,645

д;

(2)

N31

+5,333

+0,2699

—2,154

Для отыскания остальных весовых коэффициентов вычисления

выполняют по способу Ганзена, учитывают свойство весовых коэф-

фициентов Qsi = Qis, получают

Q43 = EuQw <?42 = ^2

Q43 + E

Q«\ Q

= £

14Q44

Q33 — ^34^34 + ^(2) ' ^32 = ^23^33 + ^24^34» Q2] = ^12^32 +

+ <^13^33 ^14Qs4

= £23^23 + ^24 Q24+ 77(1)

^21

—

^12^22 + 4" ^14^24

Qll =

12Ql2 + £l3Ql

+ ^14Ql4 + ^

(VI.27)

В формулах (VI.25)—(VI.27) введено обозначение Е — коэффи-

циентов элиминационных строк таблицы решения нормальных

уравнений

^ . р

"Г

210

где

л/ л/ Л^

ЛДО

= N

- n^NU,

N<$>

= N

- ^ Nu - N&.

На основании соотношений (VI.27) весовые коэффициенты вы-

числены для нескольких прямоугольных фигур с одинаковой длиной

и ориентированием исходной стороны (табл. 39).

Таблица 39

Весовые коэффициенты I : 0.5

1 : 0,75

1 : 1.25

1 : 1.5

1 : 1,75

1 : 2

Qll = «83

Qll=Q21 = -(0з4 = «4з)

Qi3=Qsi

Ql4 = Q41 = -(Q23 —Qsi)

Q22

= С? 44

«24 = С? 42

0,070

—0,033

0,007

0,056

0,232

0,055

0,164

—0,029

0,065

0,103

0,331

0,155

0,294

0,118

0,177

0,52

0,353

0,456

0,063

0,181

0,276

0,881

0,548

0,648

0,160

0,253

0,421

1,448

1,270

0,871

0,310

0,315

0,621

2,378

2,204

1,125

0,528

0,418

0,887

3,705

3,512

При этом имеем: Q

= Q

= q = q

и Q

= <?44 = <7,. = q

По данным табл. 39 можно построить график, кривые которого

покажут, что характер функций непериодический.

Для исследования характера кривых применим способ П. Л. Че-

бышева «параболического интерполирования», составив функцию

параболы высшего порядка [11].

у =

+ v

£ + v

+ + v

+ . .. . (VI.28)

Составим уравнение связи весового коэффициента: для первого

приближения, ограничиваясь тремя членами функции (VI.28), а

для второго — четырьмя, т. е.

Qis=bk* + ck + d \

= ak

+ bk

+ ck + dr

где k —

SAB : SAD

— коэффициент вытянутости прямоугольника; a,

с, d—неизвестные.

Обозначим коэффициенты при неизвестных: $=A

k] = B

ki = СУ, коэффициент при d равен 1; тогда на основании (VI.29)

составим уравнения ошибок

a + Bib + Cic + d — Q

. (VI .30)

Свободный член Q

может принимать значения любого весового

коэффициента, соответственно и ошибки и, будут принадлежать

исследуемому весовому коэффициенту.

211

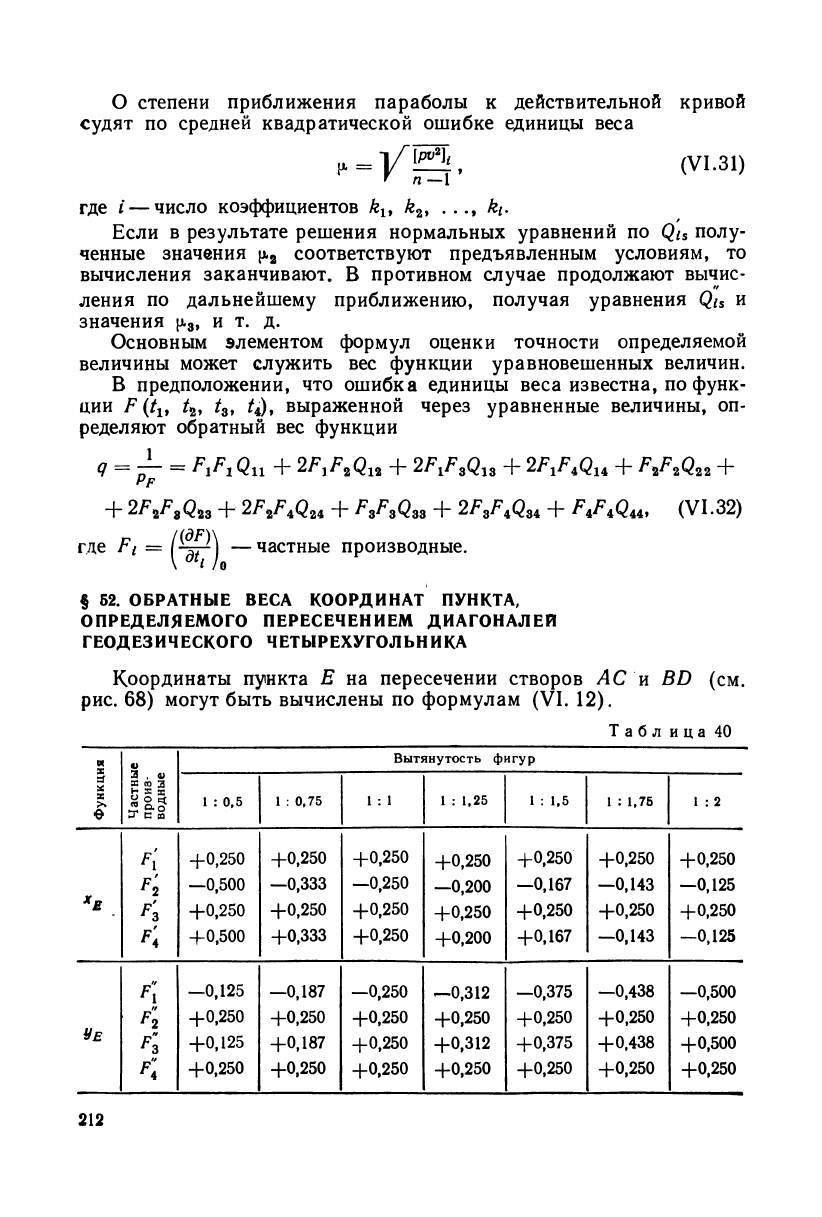
О степени приближения параболы к действительной кривой

судят по средней квадратической ошибке единицы веса

= УЩ , (VI.31)

т п— 1

где i — число коэффициентов k

..k

Если в результате решения нормальных уравнений по Qi

полу-

ченные значения [х

соответствуют предъявленным условиям, то

вычисления заканчивают. В противном случае продолжают вычис-

ления по дальнейшему приближению, получая уравнения Q

значения и т. д.

Основным элементом формул оценки точности определяемой

величины может служить вес функции уравновешенных величин.

В предположении, что ошибка единицы веса известна, по функ-

ции F (t

, /

), выраженной через уравненные величины, оп-

ределяют обратный вес функции

Q —

FIFIQU + 2 F,F

+ 2F

+ + F

+ 2F

+ 2 F

Q„ + F

+ 2F

F,Q

, + F

, (VI.32)

где F

= ^pj — частные производные.

§ 52. ОБРАТНЫЕ ВЕСА КООРДИНАТ ПУНКТА,

ОПРЕДЕЛЯЕМОГО ПЕРЕСЕЧЕНИЕМ ДИАГОНАЛЕЙ

ГЕОДЕЗИЧЕСКОГО ЧЕТЫРЕХУГОЛЬНИКА

Координаты пункта Е на пересечении створов АС и BD (см.

рис. 68) могут быть вычислены по формулам (VI. 12).

Табл ица 40

Вытяну тость фигур

ХЛ

ас

>»

3 , О

со

н я

а*

О. О

1 : 0,5

1 : 0,75

1 : 1 1 : 1,25

1 : 1,5

1 : 1,75

1 : 2

Уси

+0,250

—0,500

—0,333

—0,250

—0,200

—0,167

—0,143

—0,125

Р'г

+0,250

+0,250 +0,250 +0,250

+0,500

+0,333

+0,250

+0,200

+0,167 —0,143

—0,125

р\

—0,125

—0,187

—0,250

—0,312

—0,375

—0,438

—0,500

УЕ

Р\

+0,250

+0,250 +0,250

+0,250

УЕ

Рг

+0,125

+0,187

+0,250 +0,312

+0,375 +0,438

+0,500

+0,250

+0,250 +0,250

+0,250

212

При оценке точности координат пункта Е частные производные

функции F

находят по формуле (VI. 19).

Частные производные функции F

пункта Е (VI. 12) опреде-

ляются выражениями (VI. 21).

Для рассматриваемой сети из геодезического четырехугольни-

ка прямоугольной формы величины частных производных функций

Хе И Уе приведены в табл. 40.

Используя величины весовых коэффициентов (см. табл. 39)

и частных производных (см. табл. 40), по формуле (VI. 32) нахо-

дят обратные веса координат и положения пункта триангуляции

в пересечении прямоугольного геодезического четырехугольника

принятой вытянутости. Например, обратные веса координат точки

Е — пересечения диагоналей геодезического четырехугольника —

квадрата с основанием 1 км будут д

ХЕ

=» 0,12 и д

УЕ

= 0,07.

§ 53. ОПРЕДЕЛЕНИЕ ОБРАТНЫХ ВЕСОВ ЭЛЕМЕНТОВ

СЕТИ ТРИАНГУЛЯЦИИ

Для оценки точности определения длины стороны триангуляции

выразим ее как функцию координат пунктов

=V(XN — хнУ + (ум — Ун)

, (VI.33)

где N и Н — индексы, соответствующие номерам пунктов.

Приращение функции (VI.33) получим

= f

+ f

+ ПЪу

. (VI .34)

Для удаленной стороны частные производные будут:

h =

(^с)о =

C0S ttDC: h =

Шо =

Sin а

1 ,

с / dL\

/ dL\ . f, (VI.35)

/»=Ы,=-

cos аос:

f*=fe)

sina

поэтому по (VI.34)

&Fl

= cos a

+ sin а

ос

Ьу

— cos a

— sin <x

. (VI .36)

Поскольку сеть ориентирована так, что a ad = 0 И а

a = 0, то

LDC

=bx

— bx

. (VI.37)

В таком случае по формуле (VI.32) и так как/, = 1, а/

=—1,

ЯЬ

О0

= QN + Qss - 2Q

. (VI. 38)

Для стороны AD и ВС в соответствии с формулами (VI.32)

(VI.33)—(VI.35) будем иметь

= Qu \

Qi-вв = Qm Г (

Но Q„ = Q

, поэтому

= 4L

BQ%

213

Это в равной мере относится и к диагоналям геодезического

четырехугольника, т. е. q

LAC

= Ql

= Q

= Qu-

Если вычисленные данные по (VI.32) и (VI.38) для фигур раз-

ной вытянутости нанести на график, то линии изменения величин

обратных весов представят собой кривые непериодического характера.

Дирекционный угол направления с пункта Н на пункт N в

виде функции координат будет

Уы

— У и

= (VI. 40)

Частные производные этой функции = ^ будут

sin a

COS

Ъ = ~? —Г—

> <?2

= +

—

sin a

cos a

<Рз = + P с » ?4 = — P

(VI.41)

или, выразив и соответственно уменьшив

р"

в 10~

раз, получим sb км,

2,06" si n a

2,06" cos a

<Pl = > ?2 = + ^

2,06" sin a

2,06" cos a

Ъ = H ™ , <?4 = TJ

(VI.

42)

Приращение функции (VI.40) в соответствии с (VI.42) для сто-

роны DC = 1 км и а ос = 0 будет

Q = + - 2,06^

. (VI.43)

Обратный вес функции дирекционного угла можно вычислить

согласно (VI.32) по формуле

q*DQ = T2Q22 + <p4Q

4 + 2cp

(VI.44)

или, имея в виду равенство весовых коэффициентов и частных

производных

Чош =8,5(Q

-Q

). (VI. 45)

Наконец, подставляя значения Q

и Q

из табл. 39, можно

установить, что в геодезических четырехугольниках различной

вытянутости q

aDC

= 1.

По аналогии могут быть вычислены величины обратных весов

функций дирекционных углов и остальных сторон сети.

В подобных прямоугольных геодезических четырехугольниках

соотношение весов изменяется пропорционально квадрату длины

214

исходной стороны Sab, выраженной в километрах. Ограничивая

вытянутость в интервале 0,75-М,75, расчетные формулы будут:

= (0,25k

+ 0,08& — 0,04) sab

(VI.46)

= (\,92k

— 2,78/г + 1,36) sab

= (0,36k

— 0,05k + 0,03) s

= (0,\\k

-0,\9k + 0,20)s

= (0,25k

— 0,Ш + 0,\2)s

В геодезическом четырехугольнике прямоугольной формы со

сторонами 1,00 х 1,25 км в случае измерения длины меньшей

стороны (для k =1,25) по формулам (VI.46) найдем: q

= 0,45,

= 0,88, q

= 0,54, q

= 0,13, q

= 0,14, а при измерении длины

большей стороны (для k = 0,8) получим: q

= 0,28, q

= 0,48, q

= 0,36, q

= 0,19, д

УЕ

=0,06.

Следовательно, во втором варианте обратные веса координат

определяемых пунктов сети и расстояний между ними уменьшают-

ся не менее чем в 1,5 раза.

§ 54. ОПРЕДЕЛЕНИЕ ОШИБКИ ПОЛОЖЕНИЯ ТОЧЕК

НА СТОРОНАХ ГЕОДЕЗИЧЕСКОГО ЧЕТЫРЕХУГОЛЬНИКА

Обычно построение разбивочной сетки производят в 4 этапа

[6], [8]:

а) предварительное перенесение проекта сетки на местность

и закрепление вершин знаками;

б) производство точных линейных и угловых измерений, урав-

нительные вычисления и получение координат точек;

в) вычисление элементов редукции и смещение центров на

знаках строительной сетки;

г) контрольные измерения и оценка точности окончательных

результатов.

Однако на открытых территориях, что чаще всего имеет место

на новостройках, технология построения разбивочной сетки может

быть существенно упрощена, если центры определяемых пунктов

основной фигуры построения привести к проектному положению.

Затем на внешних сторонах сети линейными промерами опреде-

лить проектные положения вершин малых фигур, которые потом

будут служить и точками створов при определении положения

вершин заполняющих малых прямоугольных фигур [24].

Координаты любой точки створа выразим зависимостями:

*2о = Хн + (XN — Хн)

Уг о =УН + —

(УМ— УН)

(VI.47)

215

Здесь индексы Н и N у координат обозначают пункты створов:

при длинах линий s — взятый отрезок Hz

в створе HN, г

—

текущая точка в створе пунктов.

Коэффициенты при координатах пунктов в (VI.47) будем рас-

сматривать как постоянные величины. Придерживаясь изложенных

выше правил, выразим приращения функций йоординат намеченных

точек так:

5. r>

* .

(VI. 48)

Если оба пункта Н и N искомые, то, придавая различные

значения коэффициентам, например для Ъхм и by

: 0,1; 0,2; 0,8;

0,9; 1,0; для Ъх

и Ьу

: 0,9; 0,8; 0,2; 0,1; 0,0, и подставляя соот-

ветственно в (VI.48), можно получить ряд приращений функций.

На стороне DC найдем:

IF. = fi^xc + f

)

K=f*byc+hbyo\- (

Обратные веса функций координат текущей точки согласно

(VI.32) и (VI.49) и с учетом, что Q

= Q

, Q

= Q

44l

будут

<7x

= (/? + f\) Q

+ 2fJ

V2o

= (/I + /') Q22 + 2/2/4Q24 J'

(VI 50)

По створам AD и ВС согласно (VI.48) приращения функций

координат текущей точки г

будут

= fjxc = f

а обратные веса функций

1**. = f*Qn = /3Q33 \

ГТ соч

Яу

. = flQ

= /4Q44 Г

(VI

52)

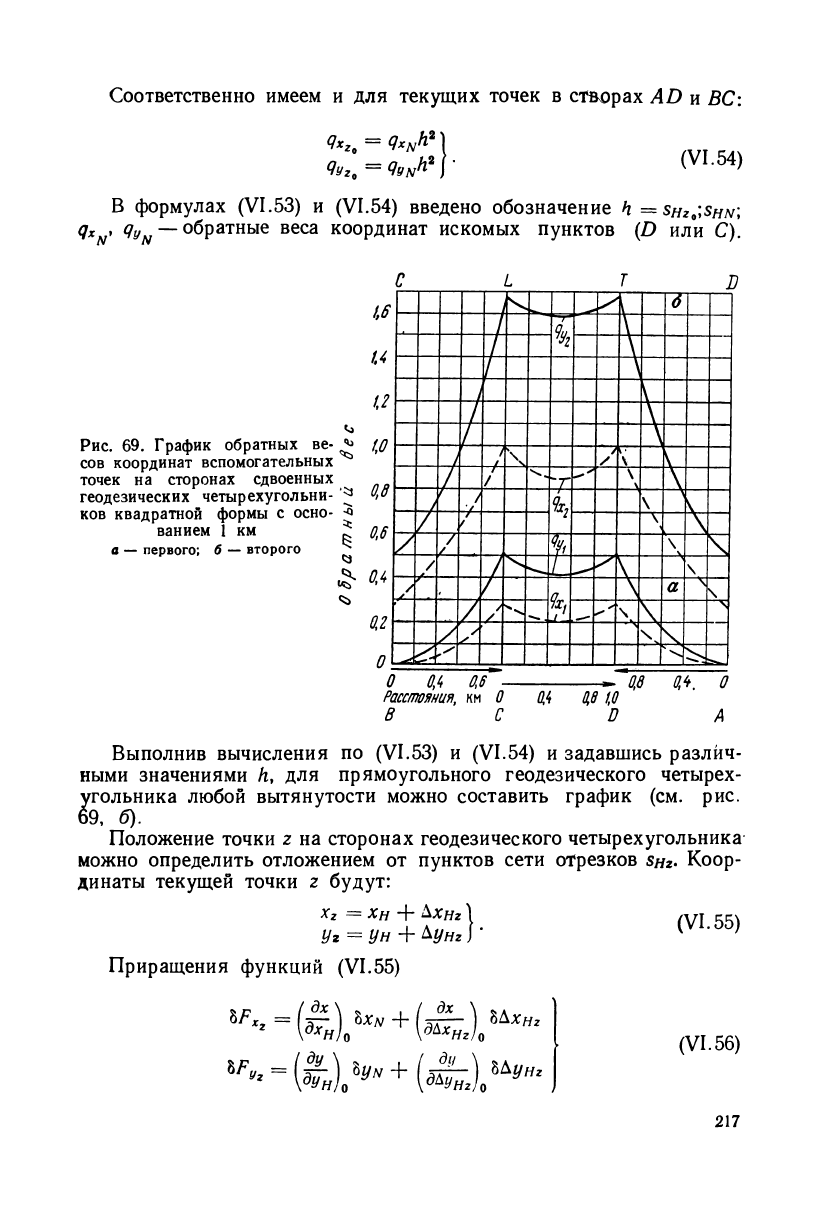
По данным вычислений на основании (VI.50) и (VI.52) для

установленных выше интервалов между точками и значениями

весовых коэффициентов геодезического четырехугольника квадратной

формы с основанием в 1 км (см. табл. 39) построен график (рис.

69, а).

Для точек на стороне DC по изложенным ранее правилам и в

соответствии с формулами (VI.28)—(VI.30) получены уравнения

обратных весов координат:

= 0,35ft»-О.ЗЙ+^1

д„

= 0,34ft

- О.ЗЗЛ + q

/• <

216

Соответственно имеем и для текущих точек в створах AD и ВС:

<?*г

= 4x

)

ЯУг

=ЯУЫ

к2

(VI.54)

В формулах (VI.53) и (VI.54) введено обозначение h =shz

\shn\

* , Яу

— обратные веса координат искомых пунктов (D или С).

1,6

Рис. 69. График обратных ве- * tf

сов координат вспомогательных

точек на сторонах сдвоенных

геодезических четырехугольни- 0, в

ков квадратной формы с осно- ^

ванием 1 км

а — первого; б — второго

£ OA

=5>

0,2

Т-

О OA 0,6 -

Расстояния,

км О

В С

М 0,81,0

0,8 ОЛ. О

Выполнив вычисления по (VI.53) и (VI.54) и задавшись различ-

ными значениями Л, для прямоугольного геодезического четырех-

угольника любой вытянутости можно составить график (см. рис.

69, б).

Положение точки z на сторонах геодезического четырехугольника

можно определить отложением от пунктов сети отрезков sm. Коор-

динаты текущей точки z будут:

Хг =Х

+ ЪХнг \

У г = УН + Ьу

Нг

) •

Приращения функций (VI.55)

Ъкунг

(VI.

55)

(VI.

56)

217