Даниленко Т.С. Организация и производство геодезических работ при крупном строительстве

Подождите немного. Документ загружается.

бетонные монолитные

знаии

бетонные пустотелые

знаки

о деревянные столбы

4-28

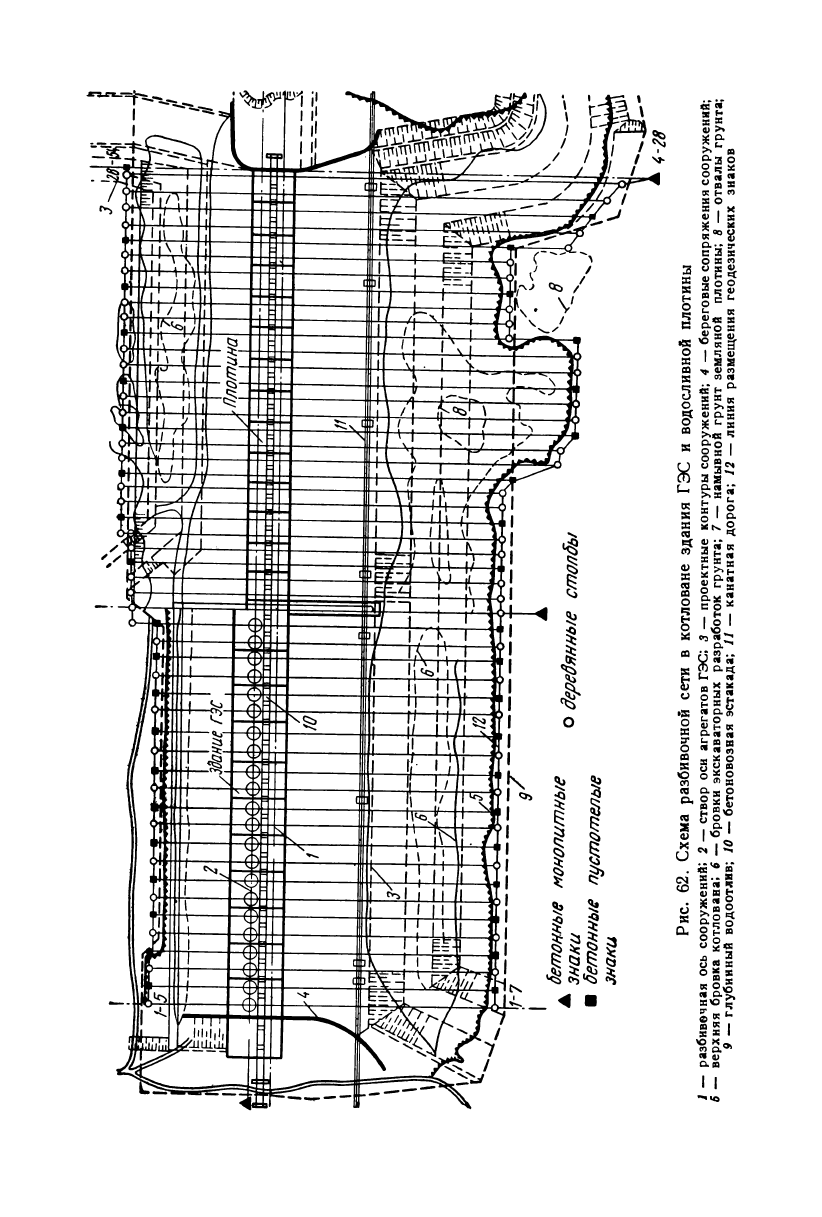
Рис. 62. Схема разбивочной сети в котловане здания ГЭС и водосливной плотины

1 — разбивочная ось сооружений; 2 — створ оси агрегатов ГЭС; 3 — проектные контуры сооружений; 4 — береговые сопряжения сооружений;

6 — верхняя бровка котлована; € — бровки экскаваторных разработок грунта; 7 — намывной грунт земляной плотины; 8 — отвалы грунта;

9 — глубинный водоотлив; 10 — бетоновозная эстакада; 11 — канатная дорога; 12 — линия размещения геодезических знаков

Разбивочная ось

сооружений.

и прочего оборудования, осуществляли непосредственными проме-

рами.

При строительстве судоходных шлюзов, как только определил-

ся контур котлована, оформились его верхние бровки, была по-

строена сеть глубинного водоотлива, проложены основные подъ-

ездные автомобильные и железные дороги, пути кабельных кранов,

стало возможным разви-

вать точную разбивоч-

ную прямоугольную сеть

(рис. 63).

Пункты этой сети зак-

репляли у бровок котло-

вана и осуществляли с

них геодезическое обслу-

живание строительных

работ до уровня днища

камер. Затем основные и

вспомогательные разби-

вочные створы перенесли

на бетон и закрепили ме-

таллическими марками, а

на боковых поверхно-

стях — створными риска-

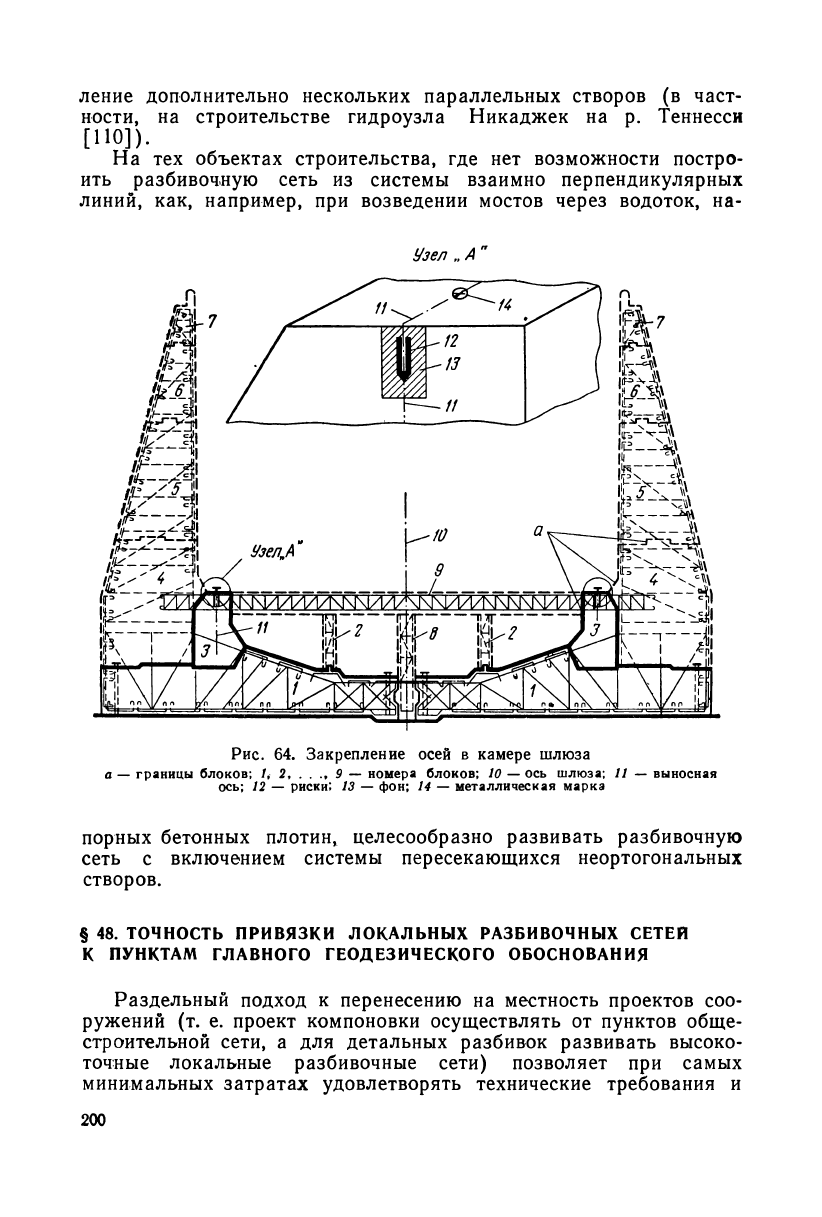
ми (рис. 64).

Особенность гидротех-

нического строительства

заметно отражается на

организации и производ-

стве геодезических работ.

Здесь нельзя ограничи-

ваться общими соображе-

ниями и рекогносциров-

кой местности, а прихо-

дится обращать присталь-

ное внимание на перспек-

тивное развитие строи-

тельного производства.

Разбивочная сеть с

постоянными створами пересечений, определяющих положение

проектных центров конструктивных элементов, освобождает от не-

обходимости производства подготовительных работ на местности

и в камеральных условиях.

Идея создания локальной разбивочной сети из прямоугольных

геометрических фигур с закреплением основных и вспомогатель-

ных разбивочных створов и осей сооружений позже привлекла

внимание и других исследователей и практиков [141].

В зарубежной практике также стали применять построение ло-

кальной разбивочной сети строго прямоугольной формы и закреп-

Условные обозначения

Д железобетонный мак с металлической,

пиранидои

о железобетонный знак

о дереВянный столб

Рис. 63.

Разбивочная сеть шлюзов перед

зачисткой котлована

199

ление дополнительно нескольких параллельных створов (в част-

ности, на строительстве гидроузла Никаджек на р. Теннесси

[110]).

На тех объектах строительства, где нет возможности постро-

ить разбивочную сеть из системы взаимно перпендикулярных

линий, как, например, при возведении мостов через водоток, на-

Узел „А"

Рис. 64. Закрепление осей в камере шлюза

а — границы блоков; /, 2, 9 — номера блоков; 10 — ось шлюза; 11 — выносная

ось; 12 — риски; 13 — фон; 14 — металлическая марка

порных бетонных плотин, целесообразно развивать разбивочную

сеть с включением системы пересекающихся неортогональных

створов.

§ 48. ТОЧНОСТЬ ПРИВЯЗКИ ЛОКАЛЬНЫХ РАЗБИВОЧНЫХ СЕТЕЙ

К ПУНКТАМ ГЛАВНОГО ГЕОДЕЗИЧЕСКОГО ОБОСНОВАНИЯ

Раздельный подход к перенесению на местность проектов соо-

ружений (т. е. проект компоновки осуществлять от пунктов обще-

строительной сети, а для детальных разбивок развивать высоко-

точные локальные разбивочные сети) позволяет при самых

минимальных затратах удовлетворять технические требования и

200

многогранные запросы строительного производства; в локальной

разбивочной сета проще оценивать ошибку в положении вынесен-

ной на местность проектной точки и центра восстановленного зна-

ка сети.

1. Если в створе линии А В (рис. 65, а) длиной L, определен-

ной с ошибкой m

измерить линию CD = /

со средней квадрати-

ческой ошибкой /л

то изменится точность определения отрезков

АС =

и DB = /

, ошибки которых обозначим соответственно т,

И /72

В предположении, что т

< m

до-

пуская пропорциональность абсолютных

величин ошибок т

и га

, т. е. /л

= j-m

=km

получим зависимость меж-

ду ошибками

т\ — ml = т

+ к

Локаль-

ная

сеть

А С

D L

откуда

Д-

(VI.

на необхо-

-О

-А

±т

L±m

Величина т

указывает

димую точность измерения отрезка

При k = 0 ошибка в длине линии ^

составит

Рис. 65. Привязка локаль-

ных сетей и точек к общей

геодезической сети

= }/т£ —

(VI. 2)

Для участков, примыкающих к основным объектам строитель-

ства, отрезки АС и DB должны определяться с предельной отно-

сительной ошибкой не менее 1 : 5000, что соответствует ошибке хо-

да полигонометрии 2 разряда (см. табл. 32).

2. На сторонах локальной разбивочной сети определяют поло-

жение проектных точек створа оси какого-либо основного кон-

структивного элемента (ось агрегатов, ось бычка и др.)-

Если сторона RQ (рис. 65,6), равная длине L, определена со

средней квадратической ошибкой ть, то, откладывая отрезки

RC = и QC = /

со средними квадратическими ошибками соот-

ветственно т

и т

, получим два положения точки С. Таким

образом, из двойного определения положения точки будем иметь

1URC

= /лг»

mQ = tni -f- /722.

Веса этих определений получим

1 1

рс

= —

И р

С%

= 2 =

L +

201

Общий вес определения положения точки равен сумме частных

весов, поэтому

L + т\ + т

PC = 9 2,22 (

)

Среднюю квадратическую ошибку положения определяемой

точки относительно пункта R выразим формулой

i (

l + m

)

тС==

2 ,

2 ' (

VL4

)

т j

-j-

3. В створах сторон локальной сети разбивочные точки соору-

жения обычно располагают с одинаковым расстоянием между

ними. В случае уничтожения одного из знаков его быстро восста-

навливают измерением по створу от соседних пунктов.

Предвычислить точность линейных измерений от смежных пунк-

тов до восстанавливаемой створной точки можно по формуле (VI.4),

при этом надо выбрать из оценки точности локальной сети зна-

чение величины m

задаться величиной тс, принять т\ =Ш2 =mi.

§ 49. ПРЕДВЫЧИСЛЕНИЕ ТОЧНОСТИ ПОСТРОЕНИЯ

РАЗБИВОЧНОЙ СЕТИ

На выбор геометрической формы разбивочной сети строитель-

ного объекта влияют многие факторы, в том числе и техническая

целесообразность и экономическая эффективность принятой кон-

струкции разбивочной сети.

Рис. 66. Схема связи раз-

бивочной сети с закреп-

ленными створами основ-

ных осей сооружений

Изыскатели обычно выносят на местность (для своих целей,

затем передают строительству) проектные точки А\В створа про-

дольной оси и C\D — поперечной оси сооружения (рис. 66, а). На

строительном объекте следует принять за исходное начало на-

правление АВ и точку О.

1. В разбивочной сети в виде ортогональных линий, совмещен-

ных или параллельных проектным осям сооружений, среднюю

202

квадратическую ошибку проектного расстояния между смежными

точками сооружения найдем

mi =moV2 (VI. 5)

— средняя квадратическая ошибка разбивки проектной точки).

Средняя ошибка в длине продольной оси сооружения, состоя-

щего из п равных секций, получится равной

=miVn. (VI.6)

Согласно СНиП III-B.5-62 ошибка в длине секции / = 60 м не

должна превышать 4- 9,6 мм.

При s=660 м, п= 11 и средней квадратической ошибке, рав-

ной половине допустимой ошибки в длине секции, по формуле

(VI.6) найдем

= ± 4,8 Уй = ± 16,0 мм.

Вспомогательные створы следует измерять со средней квадрати-

ческой ошибкой ть = m

: = =t 11,4 мм, при этом относительная

средняя квадратическая ошибка составит mb\s = 1 :58ООО.

Ошибку за непараллельность крайних створов rq и gf подсчи-

таем по формуле (И 1.59)

=-^—р, (VI. 7)

где sc—расстояние между базисами; р = 206265".

Примем s

= 700 м, ть = ± 11,4 мм, по (VI.7) найдем т

ас

= ± 4,6".

Ошибка т

ас

неперпендикулярности створа qf к А В зависит от

ошибок /я

ан

направления створа rq и т

а$у

т. е.

т\

/Па

+ ml

. (VI .8)

Дирекционное направление створа rg можно определить изме-

рением углов rgB, grB, гВА и gBA (рис. 66, а).

При равноточных измерениях ошибка уравненного угла этой

фигуры будет

Ру

/т- <

где т — средняя квадратическая ошибка измерения угла.

Ошибка передачи дирекционного угла от направления А В на

rg составит

"4 = m

Pyp

]/2 (VI. 10)

Далее поставим условие, чтобы т

ас

= ± 6", а т

а&

= ± 4,6",

тогда согласно (VI.8)

ttH

= ± 3,9",

203

а по (VI. 10) получим

т = 3,9 Y\ = ± 3,3"

Из подсчетов следует, что ранее вынесенные на местность и

закрепленные створы АВ и CD должны составлять прямой угол с

отклонением не более ± 4".

2. Для предвычисления необходимой точности измерения углов

в простой сети триангуляции из двух треугольников (рис. 66, б)

применим формулы (IV.2) и (IV.3).

Условные уравнения фигур будут

(1) + (2) + (3) +a>i=0

(4) + (5) + (6) +- = 0.

Весовая функция передачи дирекционного угла от направле-

ния rg:

/* = +(!) + (5) + (6).

В таком случае коэффициенты нормальных уравнений будут

[сю]

= 3, [аЬ\ = 0, [bb] = 3, [af] = 1, [bf] = 2, [bb] = 3.

После подстановки числовых значений в (IV.3) найдем — =

«= 1,33.

На основании формулы (IV.2), приняв т

= ± 3,0", найдем

[х = т

: —L= = ± 3,0 : VГЗЗ = ± 2,6".

Vpf

Средняя квадратическая ошибка ц единицы веса по величине

близка к средней квадратической ошибке тр угла, определяемой

по невязкам треугольников, поэтому m

s ^ = ± 2,6".

3. Если в сети измеряют все углы и базисы rq и gf, то их

уравнивают совместно под условием

М] +

[PsV

=min; (VI. 11)

здесь = — вес измеренного угла; т

— средняя квадратическая

ошибка измерения угла; — поправка в угол из уравнивания;

= ^ —

вес

измеренного значения базиса; m

—средняя квадра-

тическая ошибка измерения базиса; v

— поправка в базис из урав-

нивания.

Необходимую точность измерения углов и базисов сети устанав-

ливают в результате составления функции уравненных величин и

решения в дополнительной колонке схемы Гаусса. При этом при-

Шп m

нимают p

и — = —.

204

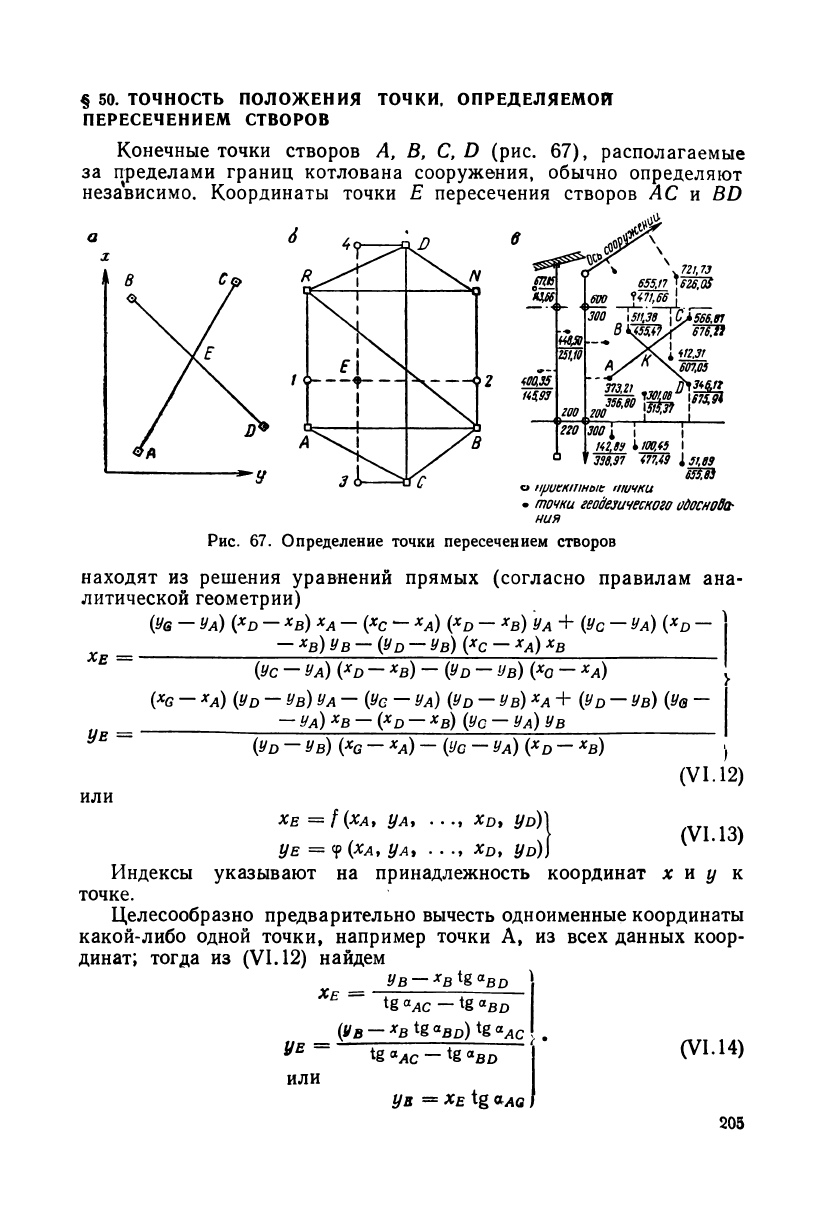
§ 50. ТОЧНОСТЬ ПОЛОЖЕНИЯ ТОЧКИ, ОПРЕДЕЛЯЕМОЙ

ПЕРЕСЕЧЕНИЕМ СТВОРОВ

Конечные точки створов А, В, С, D (рис. 67), располагаемые

за пределами границ котлована сооружения, обычно определяют

независимо. Координаты точки Е пересечения створов АС и BD

* !

м,ва

hws I

338,97

477,49

]

51,89

ШЛ

присктнош

тички

• точки

геодезического идоснода*

ния

Рис. 67. Определение точки пересечением створов

находят из решения уравнений прямых (согласно правилам ана-

литической геометрии)

(Уе

— У а) (

р —

в)

а — (

с —

а) (

d —

в) У а + (У с — У а) (

d —

—

в) Ув —

(Ур

—

Ув)

с —

а)

Уе

или

(Ус

— У a) (

d -

в) -

(Ур

- У в) (

о -

а)

(

g —

а)

(Ур

— у в) у а —

(Ус

— У а)

(Ур

— у в)

а +

(Ур

— У в)

(Уе •

—

У а)

в — (

р —

в)

(Ус

— У а) У в

(Ур

— У в) (

g -

а)

— (Ус

— У а) (

р -

в)

(VI. 12)

(VI. 13)

хе =f(XA, Уау ..хо, УР))

Уе =9 (

А, У а, . . хр, ур))

Индексы указывают на принадлежность координат х и у к

точке.

Целесообразно предварительно вычесть одноименные координаты

какой-либо одной точки, например точки А, из всех данных коор-

динат; тогда из (VI. 12) найдем

У в —

в^

вр )

ХЕ

~~ tg

<*дс

вр I

_ (Ув —

вЪ"вр) tg *ас\ .

УЕ

tg а

АС

- tg a

или

У в = Хе tg

aAQ j

(VI. 14)

205

Если совместим створ АС с осью абсцисс, то tg алв = 0, тогда

Хе = Хв — У В ctg (LBd\

(VU5)

В случае перпендикулярности створа BD к створу АС получим

хе = Хв)

Уе = 0|' <

VI16

Для оценки точности координат точки Е применим известную

формулу из теории ошибок измерений

^ = 1 (VI.

17)

где m

—средняя квадратическая ошибка определяемой величины;

ti — аргумент функций (VI. 13), принимающий значения ха, ул, ..,

(/ — порядковый номер аргумента); m

— средняя квадратичес-

кая ошибка аргумента.

Обозначая = F

Перепишем формулу (VI. 17)

ml = ^F\ml (VI. 18)

i=\

Частные производные первой функции (VI. 12) будут

Уе — Уа

• F

A —

(Ус-

•У а) — (

С —

А) tg

Ув ~~

{Ус

-Уа)—(

А) ^

Уэ — УЕ

»B -

E —

(Уо-

Ув)

(

в) tg

»B -

(Уэ

- Ув) — (

D —

B) tg

\Z/U - V О) U D J ~ \Zf U vо/ U О/

(VI. 19)

Формула (VI.17) применима для случая равноточных измерений

линейных функций. Чтобы убедиться в возможности ограничения

первичными поправками, необходимо проанализировать функцию.

Для этого следует взять вторые частные производные от исследу-

емой функции, т. е. найти • Если вторые частные производные

будут достаточно малы, то вторичные поправки можно отбросить.

В соответствии с (VI. 12) и (VI. 19) формулы вторых частных

производных будут

__о УЕ-УА

*Й*

(Ув

—

УА)

— (

С—

А)1ё

ВО

g BD

(Уп-Ув)-(*0-*в)Ъ"Ав

А6

(VI. 20)

При анализе по (VI.20) можно убедиться, что частные произ-

водные по абсолютной величине очень малы.

206

Выполняя в такой же последовательности действия и в отно-

шении второго уравнения (VI. 12), находим выражения частных

производных функций F

, которые равны частным производным

функции F

по соответствующим аргументам, умноженным на тан-

генс дирекционного угла створа, противолежащего исследуемой

точке, т. е.

= F

tg аво, Fy = Fy tg a во

F = F

Гх

—

CLAC,

*AQ

(VI.21)

Можно также убедиться в получении по вторым производным

очень малых величин.

При наиболее выгодном варианте перенесения створов olag =0

(abd = 90°) средние квадратические ошибки координат точки Е

вычисляют по формулам:

\Уп-У»1

\Уп-У*1

-(V*)'

m„ +

ГПи

(VI.22)

ошибки коор-

С I \

С/

где т

хв

, mx

, т

УА>

УС

— средние квадратические

динат точек закрепления створов.

Ошибками центрирования инструмента и визирных целей (уста-

навливаемых при помощи оптических отвесов) визирования и фик-

сирования точки можно пренебречь ввиду их незначительности.

2. Имея построенную на местности прямоугольную разбивочную

сеть (рис. 67, б), можно определять и вспомогательные створы

(например, 1—2 и 1—3). Погрешности в координатах точек 1, 2,

3, 4 вычислим по формулам:

-V

ХА

+ тм

т.

•У1

Хв

+ т

{

У г =

Хж

= т.

+ таг

т.

= m

\ т

Ух

= jf ml

+ т%

(VI.23)

в которых тл

, тв

, те,, то

— погрешности отложения на мест-

ности линий по нормалям к основным створам, которые вычисляют

по формуле (111.20).

При безошибочном значении исходных точек m

= т

Ах

\ т

У1

= 0;

Хг

= т

2\ т

Уг

= 0; т

Хг

= 0; т

Уя

= т

з; гп

Ха

= 0; m

Обозначив расстояния от точки пересечения Е до точек створов

соответственно d

, d

, по (VI.22) найдем

\2 / А \2

Ъкунг

УЕ

(VI.24)

207