Цуркин А.П., Мосолов Д.Н. Учебное пособие по курсу электротехники и электроники
Подождите немного. Документ загружается.


51
0
c
c
U
dt
Ud
RC
(6.6)
Обратим внимание на то, что свободный процесс обусловлен только внутренней
реакцией цепи на изменение ее режима, поэтому в уравнении (6) нет члена, выражающего
воздействие извне.
Уравнение цепи для свободного режима есть однородное линейное дифференциальное
уравнение первого порядка. Для его решения записывается характеристическое уравнение
RCP + 1 = 0
Решение этого уравнения
RC
P
1
Общее решение уравнения (6.6) имеет вид
RC
t
pt
c
AeAeU
Напряжение на емкости в соответствии с уравнением (6.3)
RC
t
cc
AeUU
(6.7)
Принужденная составляющая напряжения установится в цепи, когда конденсатор
зарядится, ток в цепи станет равным нулю, а напряжение на конденсаторе равно
приложенному напряжению, т.е.
EU
c
. Тогда
RC
t
c
AeEU
(6.7а)
Постоянная А определяется из начальной условий, учитывая второй закон
коммутации.
В момент включения цепи, при t=0 (момент замыкания ключа К) согласно второму
закону коммутации U
c
=0.
Из (7а) определяем А=-Е.
Таким образом, напряжение на емкости в период переходного процесса будет
изменяться следующим образом:
)1()1(
t
RC
t
c
eEeEU
(6.8)
где τ=RC - постоянная времени цепи RC.
τ имеет размерность времени.
C
B
AC
A
B
B
K
ORC
m
^
Ток переходного процесса
t
c
e
R
E
dt
dU
Ci
(6.9)
Кривые изменения U
c
=ƒ(t), U´
c
=ƒ(t), U
´´
c
=ƒ(t) и i=ƒ(t) показаны на рис.3.
В начальный момент времени t=0, i=
R
E
.
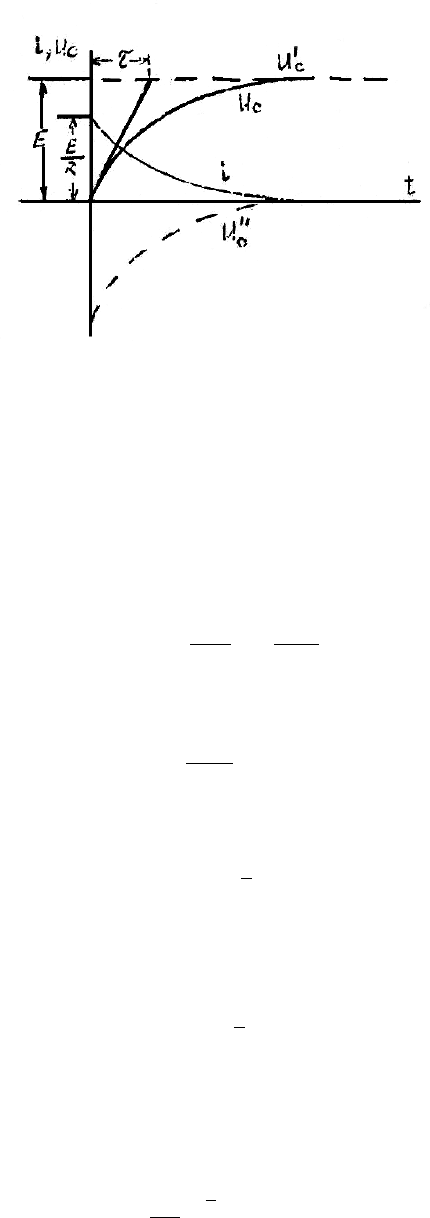
52
Рис.6.3
Рассмотрим процесс разрядки конденсатора на сопротивление R (рис6..2, когда ключ
К переведен в положение 2). После замыкания ключа К напряжение на емкости U
с
вызовет в
цепь ток i, конденсатор начнет разряжаться.
По второму закону Кирхгофа, если направления тока и напряжения совпадают,
уравнение цепи будет иметь вид
0
c
UiR
(6.10)
Принужденное напряжение U
´
и принужденный ток i
´
в цепи равны нулю.
Свободная составляющая тока
dt
Ud
C
dt
Qd
i
c
…………………………………………..(6.11)
(11)
Тогда (6.10) запишется в виде:
0
c
c
U
dt
Ud
RC
……….(6.12)
Это однородное дифференциальное уравнение первого порядка, как и уравнение (6.6).
Решение уравнения (12)
c
t
c
UAeU
C помощью второго закона коммутации определяем значение постоянной А:
при t=0, U
c
=U
0
=E.
Таким образом, напряжение на емкости при разрядке конденсатора
t
c
eUU
0
(6.13)
где τ=RC - постоянная времени цепи RC.
Уравнение для тока разрядки в цепи можно получить, если подставить U
c
в (6.10) или
(6.11).
t
e
R
U
i
0
(6.14)
Кривые изменения U
0
=ƒ(t) и i=ƒ(t) показаны на рис6..4.
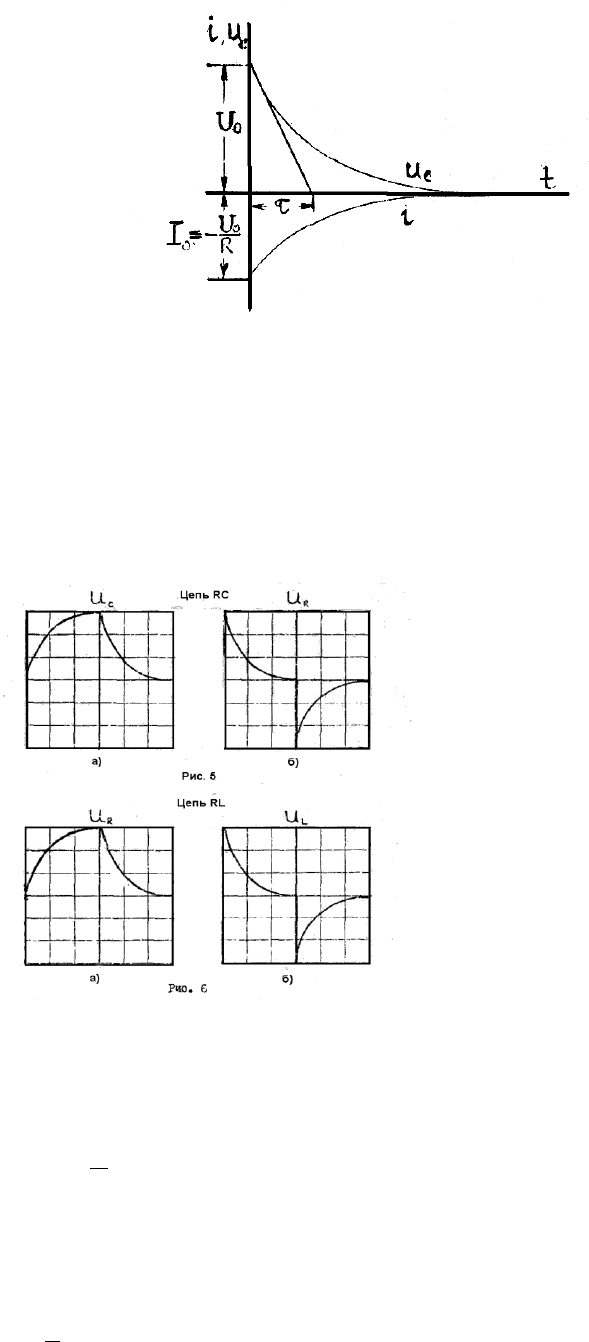
53
Рис6..4
Для цепи RL можно провести рассуждения, аналогичные тем, какие сделаны для цепи
RC.
Поскольку принужденная и свободная составляющие тока и напряжения введены для
удобства рассмотрения переходного процесса, на экране осциллографа будут только
действительные токи и напряжения.
Для общего случая, когда время замкнутого и разомкнутого состояний цепи равно
времени переходного процесса (t
пп
≈4τ), кривые изменения напряжений на элементах цепи
будут иметь вид, аналогичный показанному на рис.5 а, б (цепь RC) и на рис. 6 а, б (цепь RL).
В лабораторной работе функции ключа К выполняет генератор прямоугольных
импульсов ГПИ.
Постоянная времени цепи характеризует длительность переходного процесса
t
пп
=(3÷4)τ и составляет доли микросекунд. Для цепи RC постоянная времени τ=RC, для цепи
RL
R
L
.
Графически τ определяют следующим образом. К кривой U=ƒ(t) проводят
касательную (к любой точке кривой) и измеряют подкасательную (отрезок от точки касания
до точки пересечения касательной с асимптотой (см.рис.3 и рис.4).
Величину, обратную постоянной времени τ, называют коэффициентом затухания
1
.
Значения напряжения U и времени t определяют с помощью осциллографа, поэтому
кривые U(t) следует зарисовывать строго по клеточкам на экране осциллографа.
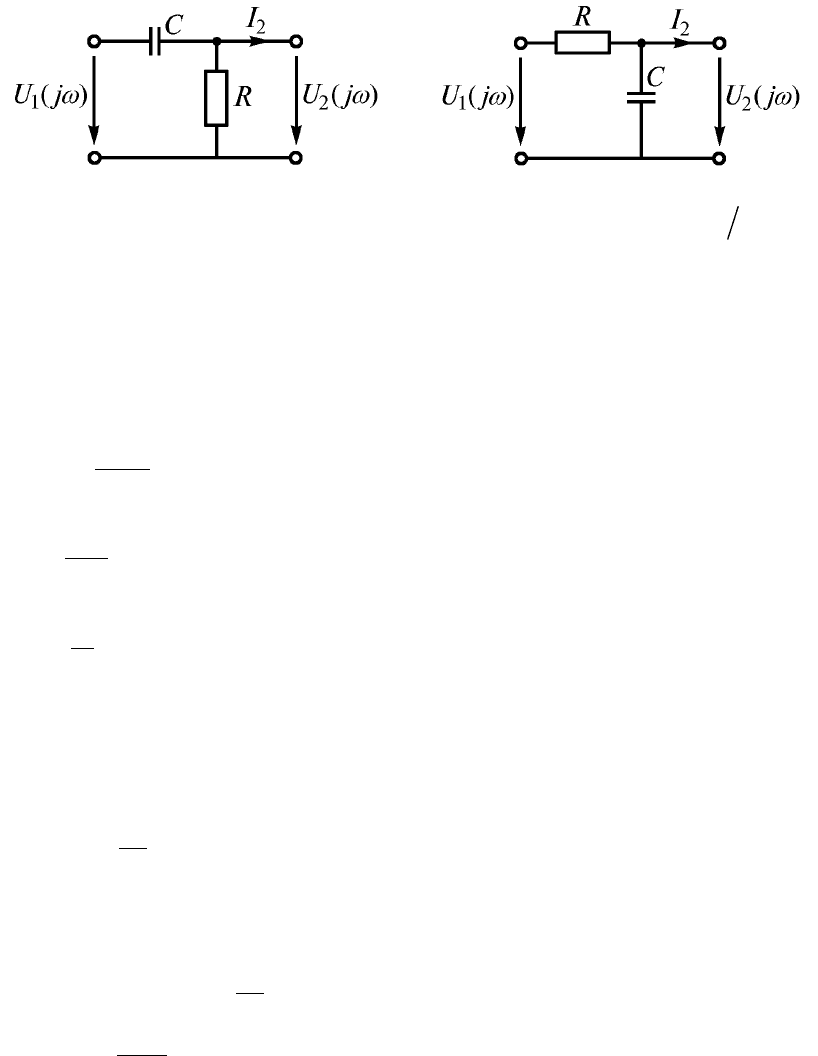
54
Тема№7.Методы расчёта переходных процессов.
На рисунке 7.1 при сопротивлении нагрузки бесконечно большом
0
2
I
. Выбрав
параметры схемы такие, что
1CR
, то
2
Uj
1
j CRU j
, значит в цепи
происходит дифференцирование входного напряжения.
Рис.7. 1 Рис. 7.2
Так же для схемы на рисунке 2, при
1CR
21
U j U j j CR
, т.е. в
цепи происходит интегрирование входного напряжения.
Какому знаку подчиняется сигнал на выходные цепи (вывод формулы)
А) Дифференц. RC
Диф.цепь – это линейный четырёхпомостник, у которого выходное и пропорц.
производной от входного.
Uвых=
dt
dUbx
dt
dUc
Cic
dt
di
LU 1
Учитывая, что ic проходит через сопр-е, для Uвых можно записать
Uвых = icR
Uвых =
dt
du
CR
Из схемы видно, что Uc = Uвх=Uвых
Учитывая что Uвых « Uвх
Уравнение Uвых =
dt
du
CR
можно записать в следующей форме.
Uвых = СR
dt
dubx
С=RС
2. Прохождение через линейные формирующие цепи с т.з. переходом процессов.
А) диф. RC
3 С = t
u
Если t
u
= 3с то за время действия входного импульса (t
u
= t
2
– t
1
) Конд. Почти
полностью зарядится и в момент t
2
, когда действие импульса закончится Uвх = 0, напр-е на

55
конд. Uc станет равен Uu (на рисунке пунктиром), а напр-е на резисторе R Ur упадёт до 0,
т.к. теперь цепь отключена от вх напр-я (Uвх = 0, Ur+Uc = 0), конд. Начнёт разряжаться и
через время t=tu напр-е на нём станет равно 0.
Так в цепи с момента t2 изменится направление, а направление на резисторе К в
момент t2 скачком будет равно Ur = -Uп и начнёт спадать по
0
t
экспоненте Ur = -UuL, а
через время t=tu станет равно 0. Т.о., на выходе цепи образуются два острокон. или полож. и
отриц. полярностей, площади которых равны, а амплитуда равна Uп.
Б) Диф. RL
Tu»С
Для рассмотрения прохождения импульса следует воспользоваться первым законом
коммутации.
В) интегр. RC
tu=3C
В момент вкл цепи напряжение на входе в силу 2-го закона коммутации = 0, а затем
конд будет заряжаться и напряжение на нём будет возрастать по экспоненц. закону.
)1(
F
t
CUпUc
По истечении времени действия импульса tu конд полностью разряд и в момент
времени t2 напр-е на нём достигнет Uп. С этого момента действие импульса на цепь
прекратится, конд начинает разряжаться по экси закону и через tп, напр-е на нём спадёт до 0.
Б) диф. RL
XI = W L
При вкл. XI очень большая
Вых напр-е снимается с катушки индуктивности
Uвых = UI = L
dt
di
Uвых =
dt
duвuв
R
L
Если посмотреть на схему, то очевидно
R
Ubx
i
R
UR
i
Ur=Uвх – Uвых
Учитывая все уравнения, запишем Uвых =
dt
duвu
R
L
R
L
C
В) интир. RC
Интер.цепь – это четырёх полюсник, у которого Uвых = K
t
0
Uвх (t) dt
Снимаем напряжение на конденсаторе, составим для данной цепи уравнение, Uвх =
RY + Uвых

56
Учитывая что Ic =
dt
dUc
C
имеем Uвх = RC
Dt
dUc
Uвых = Uвых
RC dUc=Uвх-Uвых
Разделяя переменные и интегрируя уравнение RC dUc=Uвх-Uвых получаем
Uвых =
dttUввыtUвв )()((1
1
0
Если Uвых <<Uвх, то получаем Uвых =
t
K
0
Uвх (t)dt, где
CRC
K
11
Г) интегр RL
Uвых =
0
L
R
Uвх dt
4. Применение диф. и инт. цепей.
Применение диф. цепей.
1. для выполнения математической операции дифференцирования в сочетании с
усилителями в вычислительных машинах непрерывного действия.
2. Для формирования импульсов стороконечной формы из прямоуг. импульсов.
3. Для селекции прямоуг. импульсов по длительности (выд.самые короткие)
4. В кач-ве раздел цепи в усилителях. В этом случае искл. прохождение пост.
напр-я коллектора транзистора предыдущего каскада но вход последущего.
Интигр.цепей.
1. для выполнения мат. операций интегр-я.
2. для получения линейного изменения токов и напр-ий.
3. для селекции импульсов по длительности.
4. доля получения целесообразно напр-я из прямоугольных импульсов.
При замыкании ключа ток от источника э.д.с. U потечет по цепи. Очевидно, что согласно
второму закону Кирхгофа, должно выполняться
UUU
rl
или, заменяя
l
U
и
r
U
,
получим
UIR
dt
di
L
. Учитывая что в момент переходной процедуры
прсв
iii
.
.
Дифференциальное уравнение можно записать в виде:
URii
dt
iid
L
прсв
прсв
..
..
(7.1)
При установившемся режиме
0
.
св
i
следовательно,
URi
dt
di
L
пр
пр
.
(7.2)
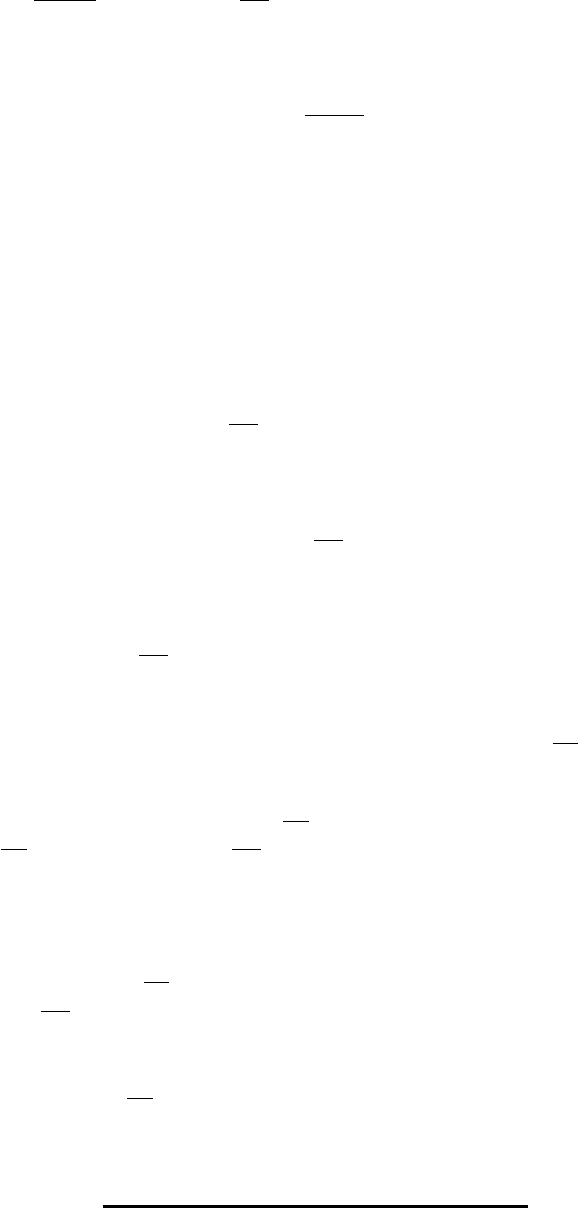
57
Очевидно, что постоянной величине приложется U,
consti
пр
.
Поэтому
0
.
dt
di
L
пр
,
R
U
i
пр
.
Вычитая уравнение 2 из 1, получим
0
.
Ri
dt
di
L
св
св
Мы получили дифференциальное уравнение первого порядка с постоянными
коэффициентами без правой части. Решаем его, пользуясь преобразованием Лапласа.
Очевидно
pt
св
Aei
.
.
Величина определиться из начальных условий при t=0
0
..
свпр
ii
Следовательно,
R
U
ii
свпр
..
.
Подставляя его в уравнение получим
pt
Ae
R
U
Следовательно
R
U
A
Оператор Лапласа Ф определиться из PL+R=0. Очевидно, что
L
R
P
.
Обозначив
R
L
j
, получим
j
t
св
e
R
U
i
.
действительный ток в цепи, определяется как
сумма токов свободного и принужденного.
)1(
.
j
t
св
e
R
U
i
Постоянная времени
R
L
j
графически представим следующим образом
Тема №8.
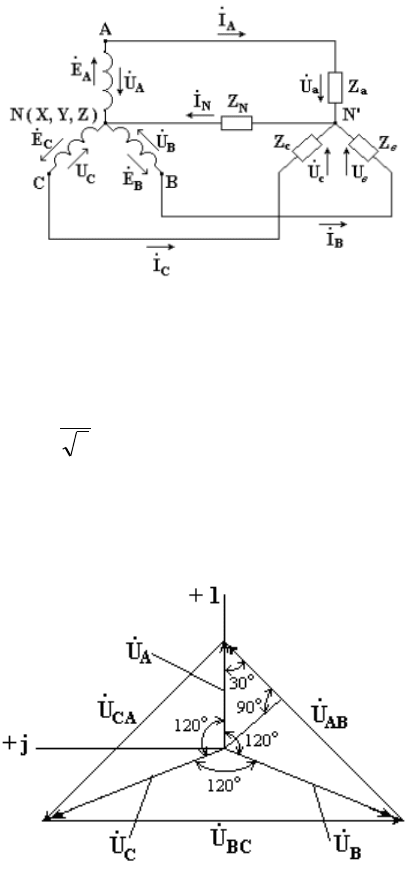
Трехфазные электрические цепи.
Три взаимно связанные электрические цепи с ЭДС одинаковой частоты и амплитуды,
но сдвинутые по фазе одна относительно другой на 1/3 периода называется трехфазной
системой переменного тока.
58
Участок трехфазной системы, по которому протекает одинаковый ток, называется
фазой.
Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и
приемников или нагрузки, которые могут быть однофазными или трехфазными.
Мгновенные значения действующих значений ЭДС имеют следующий вид:
tEe
m
sin
1
,
)120sin(
2
tEe
m
,
)240sin(
3
tEe
m
Отсюда видно, что сумма электродвижущих сил симметричной трехфазной системы в
любой момент времени равна нулю.
Если концы трех обмоток соединить в один узел, а начала будут служить для
подключения нагрузки, то такой вид соединения называют соединения обмоток генератора
звездой. При этом три обратных провода сливаются в один, называемый нулевым или
нейтральным.
РИС.8.1
При таком способе соединения напряжение между каждой фазой и нулевым
проводом называют фазным напряжением. Напряжение между фазами А-В, В-С, С-А
называют линейным напряжением.
Соотношение между напряжениями имеет следующую формулу:
3
л
ф
U
U
Внизу представлена векторная диаграмма фазных и линейных напряжений
симметричного источника.
РИС.8.2.
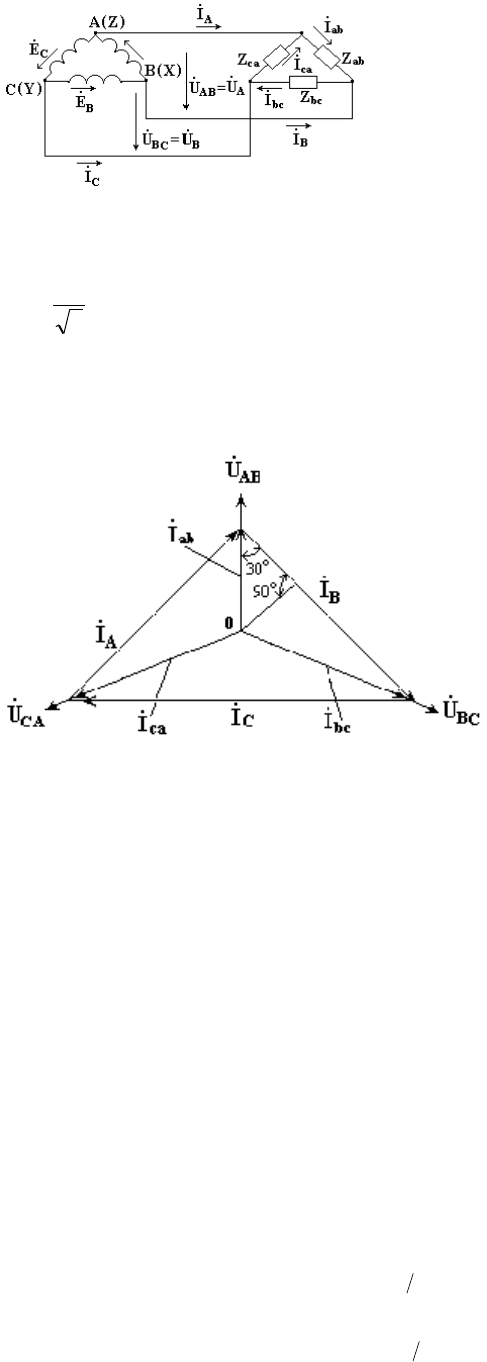
Если мы конец первой обмотки соединим с началом второй, конец второй – с началом
третьей, конец третьей – с началом первой, а узлы соединения служат отводами, то это будет
соединение треугольником.
РИС.8.3
59
При таком соединении нет различия между фазным и линейным соединением. Здесь
появляется различие между фазными и линейными токами приемника.
Соотношение между фазными и линейными токами имеет следующую формулу:
3
л
ф
I
I
Внизу представлена векторная диаграмма фазных и линейных токов симметричного
источника
РИС.8.4.
Активная мощность трехфазного генератора равна сумме активных мощностей всех
фаз:
333222111321
coscoscos
фффффф
UIUIUIPPPP
При симметричной нагрузке:
ффф
UIP
cos3
Тема №9.Периодические и апериодические несинусоидальные сигналы.
При анализе форм электрических сигналов их представляют в виде спектра частот.
Причем непериодический сигнал (импульс) представляют непрерывным, а периодический –
дискретным спектром. Для характеристики спектра применяют функцию, которая позволяет
определить закон изменения амплитуд составляющих спектра в зависимости от частоты. Иначе
ее называют спектральной плотностью. Спектральную плотность представляют амплитудно-
частотной (для четной функции частоты) или фазо-частотной (для нечетной функции)
характеристиками.
Спектральная функция импульсного сигнала продолжительностью
и высотой
макс
a
в общем виде представляет собой функцию
2
макс
2
jt
F j a e dt
.
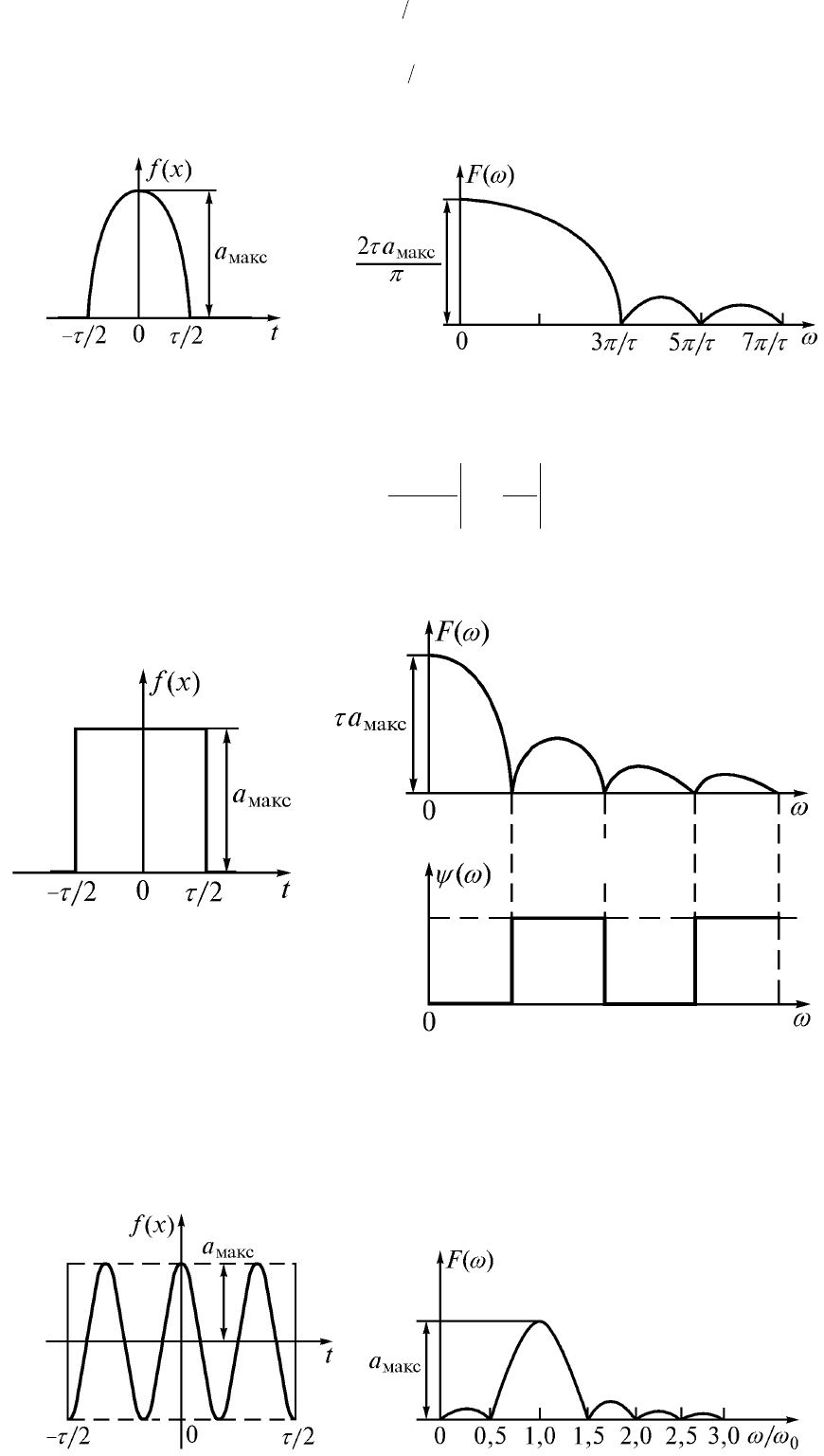
Если непериодический сигнал имеет форму импульса косинусоидальной формы, т.е.
макс
cosf x a t
длительностью
(рис.9.1 а), то его спектральная плотность
60
2
макс
2
jt
F j a e dt
.
Ниже представлена амплитудно-частотная характеристика такой функции
а) б)
Рис. 9.1
Амплитудно-частотная характеристика цепи при входном сигнале прямоугольной формы
(рис.8.2 а) длительностью
и высотой
макс
a
имеет вид (рис. 9.2 б)
макс
2
sin
2
a
Fj
.
Фазо-частотная характеристика
превращается в нуль при положительных значениях
синуса и равна
– при отрицательных (рис.9.2 б).
Рис. 9.2
При воздействии периодическим импульсом, например, синусоидальной формы, если в его
длительности укладывается целое число периодов, т.е.
nT
(рис.9.3 а), амплитудно-частотная
характеристика имеет вид, показанный на рис9.3 б.
а) б)
а)
б)
в)
