Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

This page intentionally left blank

Chapter 3

Kinematics

1. Introduction ..................... 53

2. Lagrangian and Eulerian

Speciﬁcations .................... 54

3. Eulerian and Lagrangian Descriptions:

The Particle Derivative ........... 55

4. Streamline, Path Line, and Streak

Line ............................. 57

5. Reference Frame and Streamline

Pattern .......................... 59

6. Linear Strain Rate ............... 60

7. Shear Strain Rate................ 61

8. Vorticity and Circulation ......... 62

9. Relative Motion near a Point:

Principal Axes ................... 64

10. Kinematic Considerations of

Parallel Shear Flows............ 67

11. Kinematic Considerations of Vortex

Flows .......................... 68

Solid-Body Rotation ............ 68

Irrotational Vortex .............. 70

Rankine Vortex ................. 71

12. One-, Two-, and Three-Dimensional

Flows .......................... 71

13. The Streamfunction ............. 73

14. Polar Coordinates .............. 75

Exercises ....................... 77

Supplemental Reading .......... 79

1. Introduction

Kinematics is the branch of mechanics that deals with quantities involving space and

time only. It treats variables such as displacement, velocity, acceleration, deformation,

and rotation of ﬂuid elements without referring to the forces responsible for such a

motion. Kinematics therefore essentially describes the “appearance” of a motion.

Some important kinematical concepts are described in this chapter. The forces are

considered when one deals with the dynamics of the motion, which will be discussed

in later chapters.

A few remarks should be made about the notation used in this chapter and

throughout the rest of the book. The convention followed in Chapter 2, namely,

that vectors are denoted by lowercase letters and higher-order tensors are denoted

by uppercase letters, is no longer followed. Henceforth, the number of subscripts

will specify the order of a tensor. The Cartesian coordinate directions are denoted

by (x, y, z), and the corresponding velocity components are denoted by (u, v, w).

When using tensor expressions, the Cartesian directions are denoted alternatively

DOI: 10.1016/B978-0-12-381399-2.50003-4

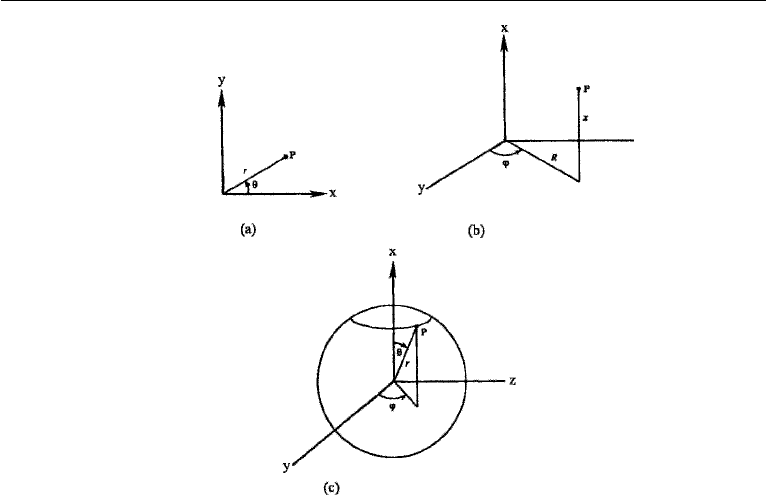
54 Kinematics

Figure 3.1 Plane, cylindrical, and spherical polar coordinates: (a) plane polar; (b) cylindrical polar;

by (x

), with the corresponding velocity components (u

). Plane

polar coordinates are denoted by (r, θ), with u

and u

the corresponding velocity

components (Figure 3.1a). Cylindrical polar coordinates are denoted by (R,ϕ,x),

with (u

) the corresponding velocity components (Figure 3.1b). Spheri-

cal polar coordinates are denoted by (r,θ,ϕ), with (u

) the corresponding

velocity components (Figure 3.1c). The method of conversion from Cartesian to

plane polar coordinates is illustrated in Section 14 of this chapter.

2. Lagrangian and Eulerian Speciﬁcations

There are two ways of describing a ﬂuid motion. In the Lagrangian description, one

essentially follows the history of individual ﬂuid particles (Figure 3.2). Consequently,

the two independent variables are taken as time and a label for ﬂuid particles. The label

can conveniently be taken as the position vector a of the particle at some reference time

t = 0. In this description, any ﬂow variable F is expressed as F(a,t). In particular,

the position vector is written as r = r(a,t), which represents the location at t of a

particle whose position was a at t = 0.

In the Eulerian description, one concentrates on what happens at a spatial point



, so that the independent variables are taken as r



and t



. (Here the primes are meant

to distinguish Lagrangian dependent variables from Eulerian independent variables.)

Flow variables are written, for example, as F(r



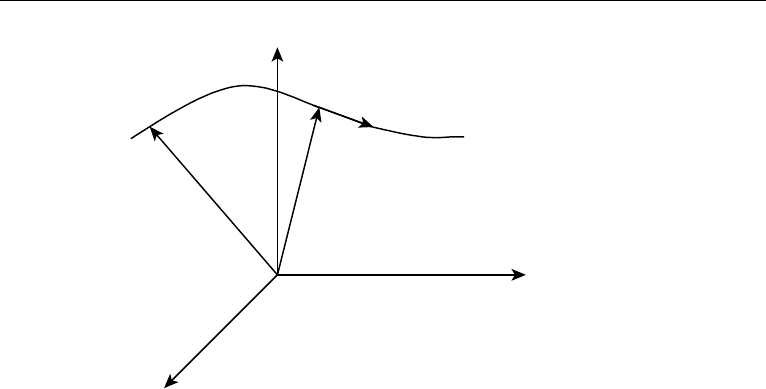
3. Eulerian and Lagrangian Descriptions: The Particle Derivative 55

r (0) 5 a

r (t)

particle

path

Figure 3.2 Particle—Lagrangian description. Independent variables: (a,t); dependent variables: r(a,t),

u = (∂r/∂t)

, ρ = ρ(a,t), and so on.

The velocity and acceleration of a ﬂuid particle in the Lagrangian description are

simply the partial time derivatives

u = ∂r/∂t, acceleration a = ∂u/∂t = ∂

r/∂t

(3.1)

as the particle identity is kept constant during the differentiation. In the Eulerian

description, however, the partial derivative ∂/∂t



gives only the local rate of change

at a point r



and is not the total rate of change as seen by the ﬂuid particle. Additional

terms are needed to form derivatives following a particle in the Eulerian description,

as explained in the next section.

The Eulerian speciﬁcation is used in most problems of ﬂuid ﬂows. The

Lagrangian description is used occasionally when we are interested in ﬁnding particle

paths of ﬁxed identity; examples can be found in Chapters 7 and 13.

3. Eulerian and Lagrangian Descriptions: The Particle

Derivative

Classical mechanics has two alternative descriptions: the ﬁeld description (Eulerian)

and the particle description (Lagrangian), associated with two of the great European

mathematical physicists of the eighteenth century [Leonhard Euler (1707–1783) and

Joseph Louis, Comte de Lagrange (1736–1813)]. Most of this book is written in

the ﬁeld description (Figure 3.3) but it is frequently very useful to express a parti-

cle derivative in the ﬁeld description. Thus we wish to compare and relate the two

descriptions.

Consider any ﬂuid property F(r



) = F(a,t) at the same position and time

in the two descriptions. F may be a scalar, vector, or tensor property. We seek to

express (∂F /∂t)

, which is the rate of change of F as seen by an observer on the

ﬁxed particle labeled by coordinate a = r(0) at t = 0, in ﬁeld variables. That is,

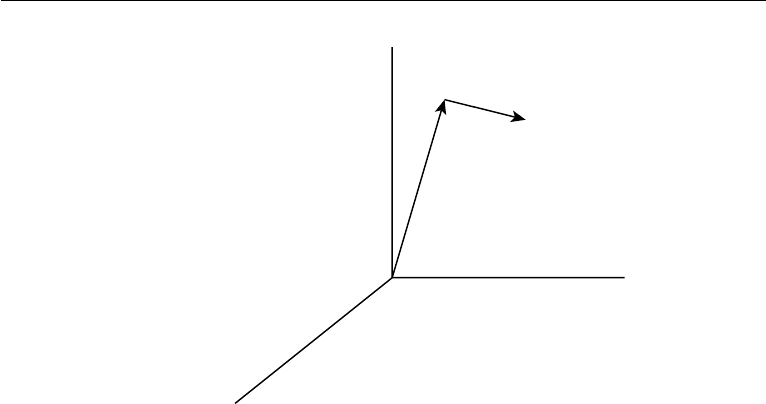
56 Kinematics

(x9, y9, z9, t9)

Figure 3.3 Field—Eulerian description. Independent variables: (x



); dependent variables:

u(r



), ρ(r



,t), and so on.

we ask what combination of r



ﬁeld derivatives corresponds to (∂F /∂t)

?Wedo

our calculation at r



= r and t



= t so we are at the same point and time in the two

descriptions. Thus

F(a,t) = F [r(a, t), t]=F(r



). (3.2)

Differentiating, taking care to differentiate dependent variables with respect to inde-

pendent variables, and using the chain rule,

[∂F(a, t)/∂t]

= (∂F /∂t



)



(∂t



/∂t ) + (∂F /∂r



)



•

(∂r



/∂r)

•

(∂r/∂t)

. (3.3)

Now ∂t



/∂t is simply the ratio of time scales used in the two descriptions. We take this

equal to 1 by measuring the time in the same units (say seconds). Here ∂r



/∂r is the

transformation matrix between the two coordinate systems. If r



and r are not rotated or

stretched with respect to each other, but with parallel axes and with lengths measured

in the same units (say meters), then ∂r



/∂r = I, the unit matrix, with elements δ

Since (∂r/∂t)

= u, we have the result

(∂F /∂t)

= ∂F /∂t



+ (∇



•

u ≡ DF/Dt. (3.4)

The total rate of change D/Dt is generally called the material derivative (also called

the substantial derivative,orparticle derivative) to emphasize the fact that the deriva-

tive is taken following a ﬂuid element. It is made of two parts: ∂F /∂t is the local

rate of change of F at a given point, and is zero for steady ﬂows. The second part

∂F /∂x

is called the advective derivative, because it is the change in F as a result

of advection of the particle from one location to another where the value of F is dif-

ferent. (In this book, the movement of ﬂuid from place to place is called “advection.”

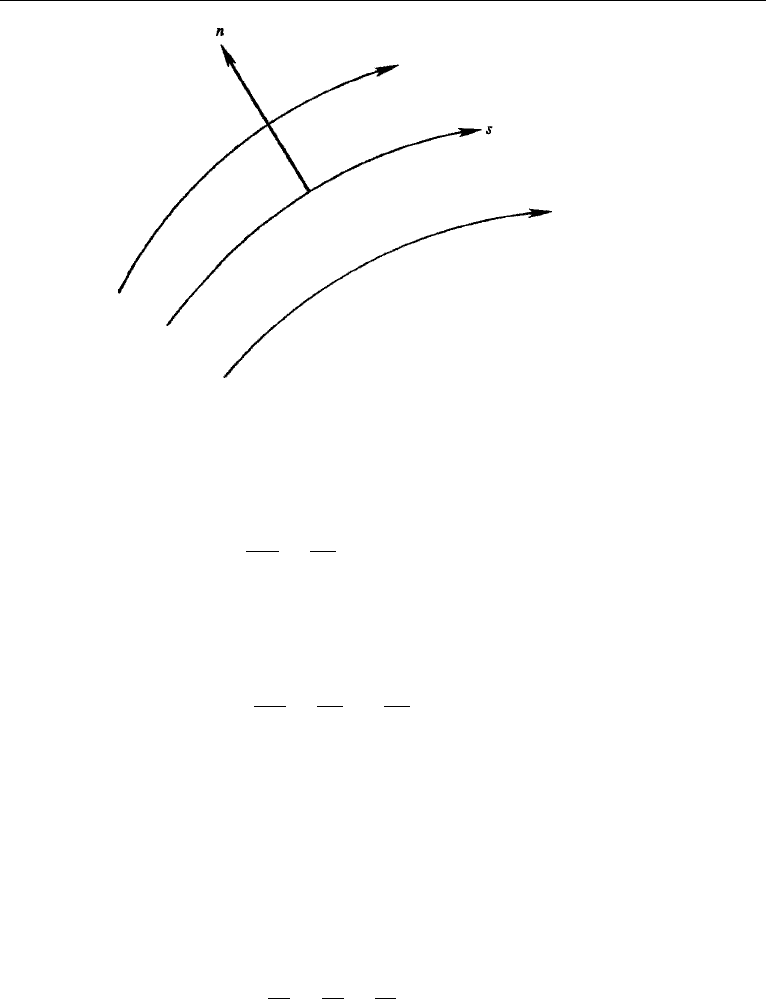
4. Streamline, Path Line, and Streak Line 57

Figure 3.4 Streamline coordinates (s, n).

Engineering texts generally call it “convection.” However, we shall reserve the term

convection to describe heat transport by ﬂuid movements.)

In vector notation, equation (3.4) is written as

∂F

∂t

+ u

•

∇F. (3.5)

The scalar product u

•

∇F is the magnitude of u times the component of ∇F in the

direction of u. It is customary to denote the magnitude of the velocity vector u by q.

Equation (3.5) can then be written in scalar notation as

∂F

∂t

+ q

∂F

∂s

, (3.6)

where the “streamline coordinate” s points along the local direction of u (Figure 3.4).

4. Streamline, Path Line, and Streak Line

At an instant of time, there is at every point a velocity vector with a deﬁnite direction.

The instantaneous curves that are everywhere tangent to the direction ﬁeld are called

the streamlines of ﬂow. For unsteady ﬂows the streamline pattern changes with time.

Let ds = (dx, dy, dz) be an element of arc length along a streamline (Figure 3.5),

and let u = (u, v, w) be the local velocity vector. Then by deﬁnition

, (3.7)

along a streamline. If the velocity components are known as a function of time, then

equation (3.7) can be integrated to ﬁnd the equation of the streamline. It is easy to

show that equation (3.7) corresponds to u ×ds = 0. All streamlines passing through

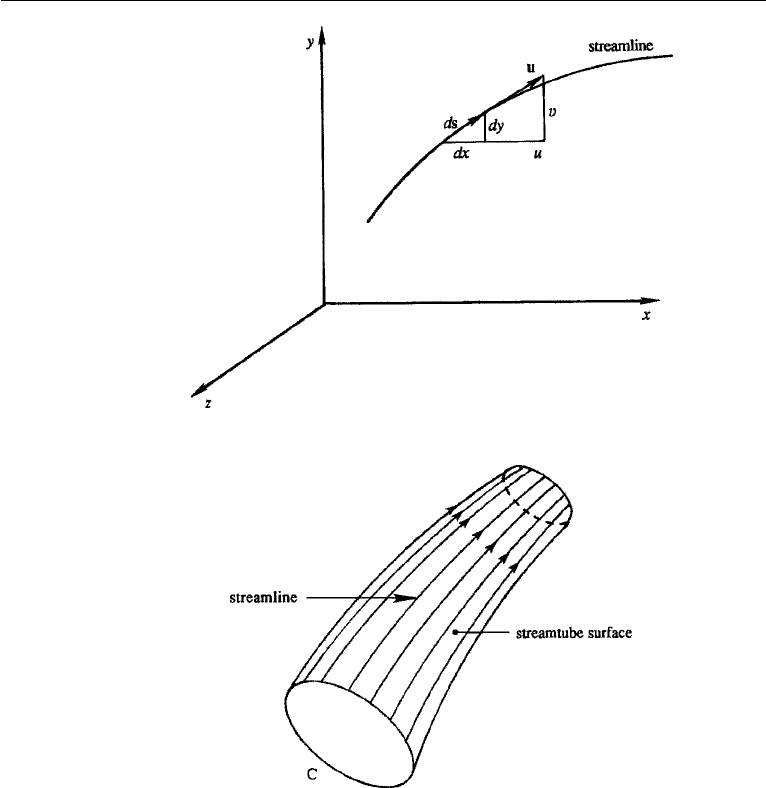
58 Kinematics

Figure 3.5 Streamline.

Figure 3.6 Streamtube.

any closed curve C at some time form a tube, which is called a streamtube (Figure 3.6).

No ﬂuid can cross the streamtube because the velocity vector is tangent to this surface.

In experimental ﬂuid mechanics, the concept of path line is important. The path

line is the trajectory of a ﬂuid particle of ﬁxed identity over a period of time. The

path line or particle path is represented as in Section 2 by r = r(a,t) where a is

the location of the particle at the reference time, say t = 0. Then u = ∂r/∂t for

ﬁxed particle. Assuming a nonzero Jacobian determinant, we may invert to obtain

the reference particle location at t = 0, a = a(r,t). Path lines and streamlines are

identical in a steady ﬂow, but not in an unsteady ﬂow. Consider the ﬂow around a

body moving from right to left in a ﬂuid that is stationary at an inﬁnite distance from

the body (Figure 3.7). The ﬂow pattern observed by a stationary observer (that is,

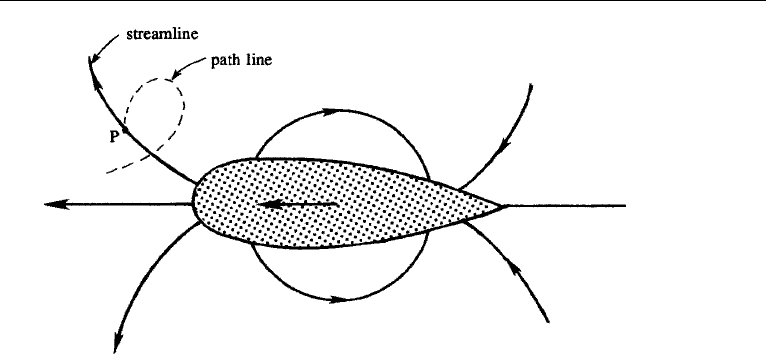
5. Reference Frame and Streamline Pattern 59

Figure 3.7 Several streamlines and a path line due to a moving body.

an observer stationary with respect to the undisturbed ﬂuid) changes with time, so

that to the observer this is an unsteady ﬂow. The streamlines in front of and behind

the body are essentially directed forward as the body pushes forward, and those

on the two sides are directed laterally. The path line (shown dashed in Figure 3.7)

of the particle that is now at point P therefore loops outward and forward again as the

body passes by.

The streamlines and path lines of Figure 3.7 can be visualized in an experiment

by suspending aluminum or other reﬂecting materials on the ﬂuid surface, illuminated

by a source of light. Suppose that the entire ﬂuid is covered with such particles, and a

brief time exposure is made. The photograph then shows short dashes, which indicate

the instantaneous directions of particle movement. Smooth curves drawn through

these dashes constitute the instantaneous streamlines. Now suppose that only a few

particles are introduced, and that they are photographed with the shutter open for a

long time. Then the photograph shows the paths of a few individual particles, that is,

their path lines.

A streak line is another concept in ﬂow visualization experiments. It is deﬁned as

the current location of all ﬂuid particles that have passed through a ﬁxed spatial point

at a succession of previous times. It is determined by injecting dye or smoke at a ﬁxed

point for an interval of time. Suppose a particle on a streak line passes the location of

dye ξ at a time τ ≤ t. Then the equation of the streak line is x = x[a(ξ , τ), t]. See

Aris (1962), Chapter 4 for more details. In steady ﬂow the streamlines, path lines,

and streak lines all coincide.

5. Reference Frame and Streamline Pattern

A ﬂow that is steady in one reference frame is not necessarily so in another. Consider

the ﬂow past a ship moving at a steady velocity U, with the frame of reference (that

is, the observer) attached to the river bank (Figure 3.8a). To this observer the local

ﬂow characteristics appear to change with time, and thus appear to be unsteady. If,

60 Kinematics

Figure 3.8 Flow past a ship with respect to two observers: (a) observer on river bank; (b) observer on ship.

on the other hand, the observer is standing on the ship, the ﬂow pattern is steady

(Figure 3.8b). The steady ﬂow pattern can be obtained from the unsteady pattern of

Figure 3.8a by superposing on the latter a velocity U to the right. This causes the

ship to come to a halt and the river to move with velocity U at inﬁnity. It follows that

any velocity vector u in Figure 3.8b is obtained by adding the corresponding velocity

vector u



of Figure 3.8a and the free stream velocity vector U.

6. Linear Strain Rate

A study of the dynamics of ﬂuid ﬂows involves determination of the forces on an

element, which depend on the amount and nature of its deformation, or strain. The

deformation of a ﬂuid is similar to that of a solid, where one deﬁnes normal strain as

the change in length per unit length of a linear element, and shear strain as change

ofa90

◦

angle. Analogous quantities are deﬁned in a ﬂuid ﬂow, the basic difference

being that one deﬁnes strain rates in a ﬂuid because it continues to deform.

Consider ﬁrst the linear or normal strain rate of a ﬂuid element in the x

direction

(Figure 3.9). The rate of change of length per unit length is

δx

(δx

) =



− AB

δx



δx

∂u

∂x

δx

dt − δx



∂u

∂x

The material derivative symbol D/Dt has been used because we have implicitly

followed a ﬂuid particle. In general, the linear strain rate in the α direction is

∂u

∂x

, (3.8)

where no summation over the repeated index α is implied. Greek symbols such as α

and β are commonly used when the summation convention is violated.

The sum of the linear strain rates in the three mutually orthogonal directions

gives the rate of change of volume per unit volume, called the volumetric strain rate

(also called the bulk strain rate). To see this, consider a ﬂuid element of sides δx

7. Shear Strain Rate 61

Figure 3.9 Linear strain rate. Here, A



= AB + BB



− AA



δx

, and δx

. Deﬁning δᐂ ≡ δx

δx

, the volumetric strain rate is

δᐂ

(δ

ᐂ) =

δx

(δx

δx

(δx

) +

δx

(δx

) +

δx

(δx

that is,

δᐂ

(δ

ᐂ) =

∂u

∂x

∂u

∂x

∂u

∂x

∂u

∂x

. (3.9)

The quantity ∂u

/∂x

is the sum of the diagonal terms of the velocity gradient

tensor ∂u

/∂x

. As a scalar, it is invariant with respect to rotation of coordinates.

Equation (3.9) will be used later in deriving the law of conservation of mass.

7. Shear Strain Rate

In addition to undergoing normal strain rates, a ﬂuid element may also simply deform

in shape. The shear strain rate of an element is deﬁned as the rate of decrease of the

angle formed by two mutually perpendicular lines on the element. The shear strain so

calculated depends on the orientation of the line pair. Figure 3.10 shows the position

of an element with sides parallel to the coordinate axes at time t, and its subsequent

position at t +dt. The rate of shear strain is

dα + dβ



δx



∂u

∂x

δx



δx



∂u

∂x

δx



∂u

∂x

∂u

∂x

. (3.10)

An examination of equations (3.8) and (3.10) shows that we can describe the

deformation of a ﬂuid element in terms of the strain rate tensor

≡



∂u

∂x

∂u

∂x



(3.11)