Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

32 Cartesian Tensors

the stresses on any arbitrary plane can then be determined. To ﬁnd the stresses on any

arbitrary surface, we shall consider a rotated coordinate system x



one of whose

axes is perpendicular to the given surface. It can be shown by a force balance on a

tetrahedron element (see, e.g., Sommerfeld (1964), page 59) that the components of

τ in the rotated coordinate system are



= C

. (2.12)

Note the similarity between the transformation rule equation (2.8) for a vector, and the

rule equation (2.12). In equation (2.8) the ﬁrst index of C is summed, while its second

index is free. The rule equation (2.12) is identical, except that this happens twice. A

quantity that obeys the transformation rule equation (2.12) is called a second-order

tensor.

The transformation rule equation (2.12) can be expressed as a matrix product.

Rewrite equation (2.12) as



= C

which, with adjacent dummy indices, represents the matrix product



= C

•

This says that the tensor τ in the rotated frame is found by multiplying C by τ and

then multiplying the product by C

The concepts of tensor and matrix are not quite the same. A matrix is any arrange-

ment of elements, written as an array. The elements of a matrix represent the compo-

nents of a tensor only if they obey the transformation rule equation (2.12).

Tensors can be of any order. In fact, a scalar can be considered a tensor of zero

order, and a vector can be regarded as a tensor of ﬁrst order. The number of free

indices correspond to the order of the tensor. For example, A is a fourth-order tensor

if it has four free indices, and the associated 81 components change under the rotation

of the coordinate system according to



mnpq

= C

ij kl

. (2.13)

Tensors of various orders arise in ﬂuid mechanics. Some of the most frequently

used are the stress tensor τ

and the velocity gradient tensor ∂u

/∂x

. It can be shown

that the nine products u

formed from the components of the two vectors u and

v also transform according to equation (2.12), and therefore form a second-order

tensor. In addition, certain “isotropic” tensors are also frequently used; these will be

discussed in Section 7.

5. Contraction and Multiplication

When the two indices of a tensor are equated, and a summation is performed over

this repeated index, the process is called contraction. An example is

6. Force on a Surface 33

= A

+ A

which is the sum of the diagonal terms. Clearly, A

is a scalar and therefore inde-

pendent of the coordinate system. In other words, A

is an invariant. (There are

three independent invariants of a second-order tensor, and A

is one of them; see

Exercise 5.)

Higher-order tensors can be formed by multiplying lower tensors. If u and v are

vectors, then the nine components u

form a second-order tensor. Similarly, if A

and B are two second-order tensors, then the 81 numbers deﬁned by P

ij kl

≡ A

transform according to equation (2.13), and therefore form a fourth-order tensor.

Lower-order tensors can be obtained by performing contraction on these multi-

plied forms. The four contractions of A

are

= B

= (B

•

= A

= (A

•

= A

= (A

•

)

= (A

•

(2.14)

All four products in the preceding are second-order tensors. Note in equation (2.14)

how the terms have been rearranged until the summed index is adjacent, at which

point they can be written as a product of matrices.

The contracted product of a second-order tensor A and a vector u is a vector. The

two possibilities are

= (A

•

= A

= (A

•

The doubly contracted product of two second-order tensors A and B is a scalar. The

two possibilities are A

(which can be written as A :B in boldface notation) and

(which can be written as A :B

6. Force on a Surface

A surface area has a magnitude and an orientation, and therefore should be treated as

a vector. The orientation of the surface is conveniently speciﬁed by the direction of

a unit vector normal to the surface. If dA is the magnitude of an element of surface

and n is the unit vector normal to the surface, then the surface area can be written as

the vector

dA = n dA.

Suppose the nine components of the stress tensor with respect to a given set of

Cartesian coordinates are given, and we want to ﬁnd the force per unit area on a

surface of given orientation n (Figure 2.5). One way of determining this is to take

a rotated coordinate system, and use equation (2.12) to ﬁnd the normal and shear

stresses on the given surface. An alternative method is described in what follows.

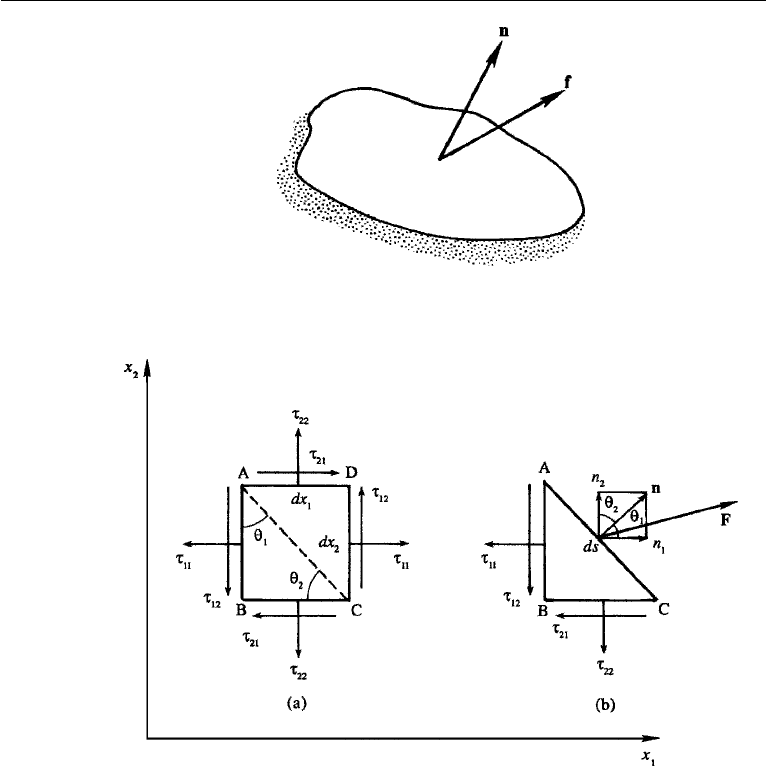
34 Cartesian Tensors

Figure 2.5 Force f per unit area on a surface element whose outward normal is n.

Figure 2.6 (a) Stresses on surfaces of a two-dimensional element; (b) balance of forces on element ABC.

For simplicity, consider a two-dimensional case, for which the known stress

components with respect to a coordinate system x

are shown in Figure 2.6a. We

want to ﬁnd the force on the face AC, whose outward normal n is known (Figure 2.6b).

Consider the balance of forces on a triangular element ABC, with sides AB = dx

BC = dx

, and AC = ds; the thickness of the element in the x

direction is unity. If

F is the force on the face AC, then a balance of forces in the x

direction gives the

component of F in that direction as

= τ

+ τ

6. Force on a Surface 35

Dividing by ds, and denoting the force per unit area as f = F/ds, we obtain

= τ

+ τ

= τ

cos θ

+ τ

cos θ

= τ

+ τ

where n

= cos θ

and n

= cos θ

because the magnitude of n is unity (Figure 2.6b).

Using the summation convention, the foregoing can be written as f

= τ

, where

j is summed over 1 and 2. A similar balance of forces in the x

direction gives

= τ

. Generalizing to three dimensions, it is clear that

= τ

Because the stress tensor is symmetric (which will be proved in the next chapter),

that is, τ

= τ

, the foregoing relation can be written in boldface notation as

f = n

•

τ. (2.15)

Therefore, the contracted or “inner” product of the stress tensor τ and the unit outward

vector n gives the force per unit area on a surface. Equation (2.15) is analogous to

= u

•

n, where u

is the component of the vector u along unit normal n; however,

whereas u

is a scalar, f in equation (2.15) is a vector.

Example 2.1. Consider a two-dimensional parallel ﬂow through a channel. Take

as the coordinate system, with x

parallel to the ﬂow. The viscous stress tensor

at a point in the ﬂow has the form

τ =



0 a

a 0



where the constant a is positive in one half of the channel, and negative in the other

half. Find the magnitude and direction of force per unit area on an element whose

outward normal points at 30

◦

to the direction of ﬂow.

Solution by using equation (2.15): Because the magnitude of n is 1 and it points

at 30

◦

to the x

axis (Figure 2.7), we have

n =



√

3/2

1/2



The force per unit area is therefore

f = τ

•

n =



0 a

a 0



√

3/2

1/2





a/2

√

3 a/2







The magnitude of f is

f = (f

+ f

)

1/2

=|a|.

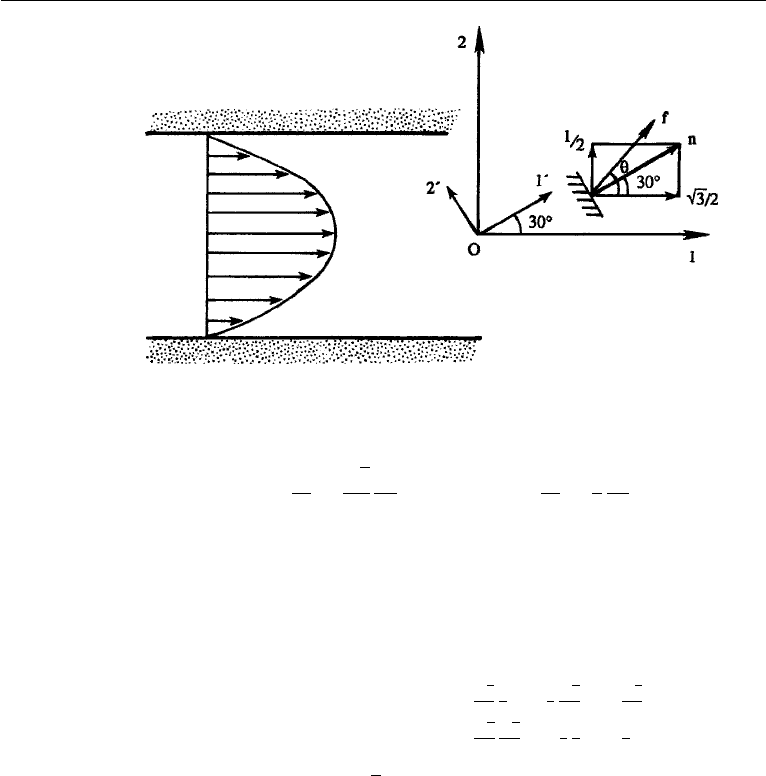
36 Cartesian Tensors

Figure 2.7 Determination of force on an area element (Example 2.1).

If θ is the angle of f with the x

axis, then

sin θ =

√

|a|

and cos θ =

|a|

Thus θ = 60

◦

if a is positive (in which case both sin θ and cos θ are positive), and

θ = 240

◦

if a is negative (in which case both sin θ and cos θ are negative).

Solution by using equation (2.12): Take a rotated coordinate system x



with x



axis coinciding with n (Figure 2.7). Using equation (2.12), the components

of the stress tensor in the rotated frame are



= C

+ C

√

a +

√

a =

√



= C

+ C

√

a −

a =

The normal stress is therefore

√

3 a/2, and the shear stress is a/2. This gives a

magnitude a and a direction 60

◦

or 240

◦

depending on the sign of a.

7. Kronecker Delta and Alternating Tensor

The Kronecker delta is deﬁned as



1ifi = j

0ifi = j

, (2.16)

which is written in the matrix form as

δ =





100

010

001





8. Dot Product 37

The most common use of the Kronecker delta is in the following operation: If we

have a term in which one of the indices of δ

is repeated, then it simply replaces the

dummy index by the other index of δ

. Consider

= δ

+ δ

The right-hand side is u

when i = 1, u

when i = 2, and u

when i = 3. Therefore

= u

. (2.17)

From its deﬁnition it is clear that δ

is an isotropic tensor in the sense that its

components are unchanged by a rotation of the frame of reference, that is, δ



= δ

Isotropic tensors can be of various orders. There is no isotropic tensor of ﬁrst order,

and δ

is the only isotropic tensor of second order. There is also only one isotropic

tensor of third order. It is called the alternating tensor or permutation symbol, and is

deﬁned as

ij k











1ifij k = 123, 231, or 312 (cyclic order),

0 if any two indices are equal,

−1ifij k = 321, 213, or 132 (anticyclic order).

(2.18)

From the deﬁnition, it is clear that an index on ε

ij k

can be moved two places (either

to the right or to the left) without changing its value. For example, ε

ij k

= ε

jki

where

i has been moved two places to the right, and ε

ij k

= ε

kij

where k has been moved

two places to the left. For a movement of one place, however, the sign is reversed.

For example, ε

ij k

=−ε

ikj

where j has been moved one place to the right.

A very frequently used relation is the epsilon delta relation

ij k

klm

= δ

− δ

(2.19)

The reader can verify the validity of this relationship by taking some values for ij lm.

Equation (2.19) is easy to remember by noting the following two points: (1) The

adjacent index k is summed; and (2) the ﬁrst two indices on the right-hand side,

namely, i and l, are the ﬁrst index of ε

ij k

and the ﬁrst free index of ε

klm

. The remaining

indices on the right-hand side then follow immediately.

8. Dot Product

The dot product of two vectors u and v is deﬁned as the scalar

•

v = v

•

u = u

+ u

= u

It is easy to show that u

•

v = uv cos θ, where u and v are the magnitudes and θ is the

angle between the vectors. The dot product is therefore the magnitude of one vector

times the component of the other in the direction of the ﬁrst. Clearly, the dot product

•

v is equal to the sum of the diagonal terms of the tensor u

38 Cartesian Tensors

9. Cross Product

The cross product between two vectors u and v is deﬁned as the vector w whose

magnitude is uv sin θ, where θ is the angle between u and v, and whose direction is

perpendicular to the plane of u and v such that u, v, and w form a right-handed system.

Clearly, u × v =−v × u, and the unit vectors obey the cyclic rule a

× a

= a

.It

is easy to show that

u × v = (u

− u

+ (u

− u

+ (u

− u

, (2.20)

which can be written as the symbolic determinant

u × v =



In indicial notation, the k-component of u × v can be written as

(u × v)

= ε

ij k

= ε

kij

(2.21)

As a check, for k = 1 the nonzero terms in the double sum in equation (2.21) result

from i = 2, j = 3, and from i = 3, j = 2. This follows from the deﬁnition

equation (2.18) that the permutation symbol is zero if any two indices are equal. Then

equation (2.21) gives

(u × v)

= ε

ij 1

= ε

231

+ ε

321

= u

− u

which agrees with equation (2.20). Note that the second form of equation (2.21) is

obtained from the ﬁrst by moving the index k two places to the left; see the remark

below equation (2.18).

10. Operator ∇: Gradient, Divergence, and Curl

The vector operator “del”

is deﬁned symbolically by

∇ ≡ a

∂

∂x

+ a

∂

∂x

+ a

∂

∂x

= a

∂

∂x

. (2.22)

When operating on a scalar function of position φ, it generates the vector

∇φ = a

∂φ

∂x

The inverted Greek delta is called a “nabla” (ναβλα). The origin of the word is from the Hebrew

(pronounced navel), which means lyre, an ancient harp-like stringed instrument. It was on this

instrument that the boy, David, entertained King Saul (Samuel II) and it is mentioned repeatedly

in Psalms as a musical instrument to use in the praise of God.

10. Operator ∇: Gradient, Divergence, and Curl 39

whose i-component is

(∇φ)

∂φ

∂x

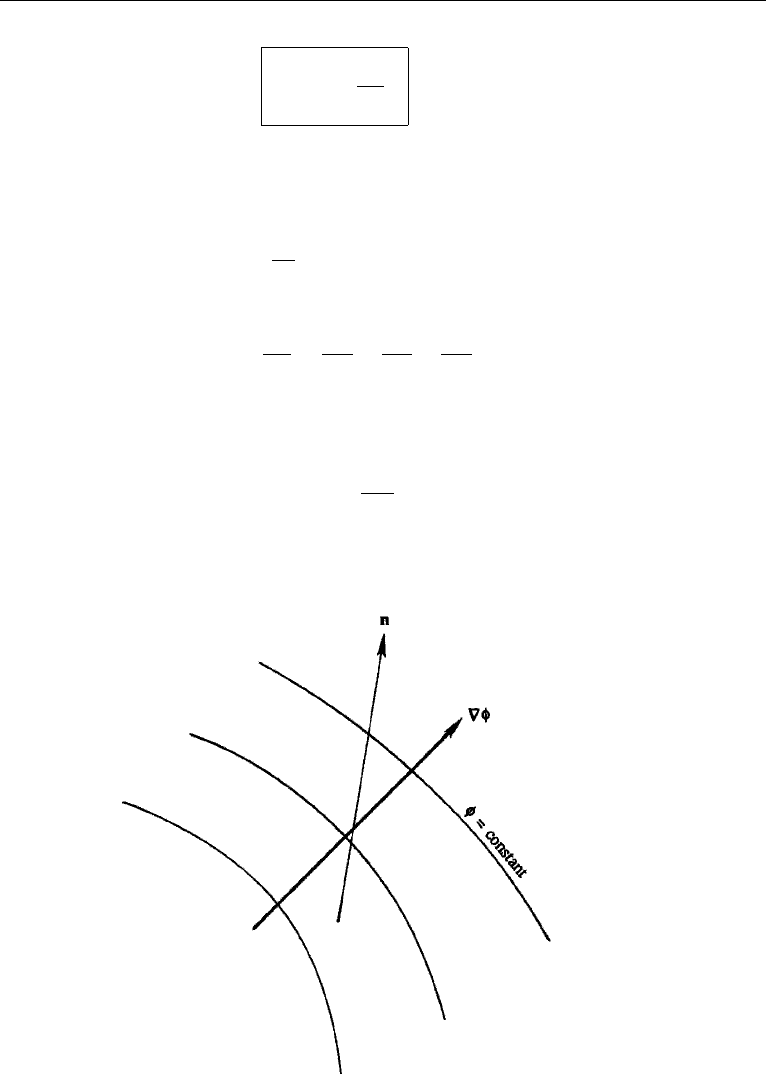
The vector ∇φ is called the gradient of φ. It is clear that ∇φ is perpendicular to the

φ = constant lines and gives the magnitude and direction of the maximum spatial rate

of change of φ (Figure 2.8). The rate of change in any other direction n is given by

∂φ

∂n

= (∇φ)

•

The divergence of a vector ﬁeld u is deﬁned as the scalar

∇

•

u ≡

∂u

∂x

∂u

∂x

∂u

∂x

∂u

∂x

. (2.23)

So far, we have deﬁned the operations of the gradient of a scalar and the diver-

gence of a vector. We can, however, generalize these operations. For example, we can

deﬁne the divergence of a second-order tensor τ as the vector whose i-component is

(∇

•

τ)

∂τ

∂x

It is evident that the divergence operation decreases the order of the tensor by one.

In contrast, the gradient operation increases the order of a tensor by one, changing

Figure 2.8 Lines of constant φ and the gradient vector ∇φ.

40 Cartesian Tensors

a zero-order tensor to a ﬁrst-order tensor, and a ﬁrst-order tensor to a second-order

tensor.

The curl of a vector ﬁeld u is deﬁned as the vector ∇ × u, whose i-component

can be written as (using equations (2.21) and (2.22))

(∇ × u)

= ε

ij k

∂u

∂x

(2.24)

The three components of the vector ∇ × u can easily be found from the right-hand

side of equation (2.24). For the i = 1 component, the nonzero terms in the double

sum in equation (2.24) result from j = 2, k = 3, and from j = 3, k = 2. The three

components of ∇ × u are ﬁnally found as



∂u

∂x

−

∂u

∂x





∂u

∂x

−

∂u

∂x



, and



∂u

∂x

−

∂u

∂x



. (2.25)

A vector ﬁeld u is called solenoidal if ∇

•

u = 0, and irrotational if ∇ × u = 0. The

word “solenoidal” refers to the fact that the magnetic induction B always satisﬁes

∇

•

B = 0 . This is because of the absence of magnetic monopoles. The reason for the

word “irrotational” will be clear in the next chapter.

11. Symmetric and Antisymmetric Tensors

A tensor B is called symmetric in the indices i and j if the components do not change

when i and j are interchanged, that is, if B

= B

. The matrix of a second-order

tensor is therefore symmetric about the diagonal and made up of only six distinct

components. On the other hand, a tensor is called antisymmetric if B

=−B

.An

antisymmetric tensor must have zero diagonal terms, and the off-diagonal terms must

be mirror images; it is therefore made up of only three distinct components. Any

tensor can be represented as the sum of a symmetric part and an antisymmetric part.

For if we write

+ B

) +

− B

)

then the operation of interchanging i and j does not change the ﬁrst term, but changes

the sign of the second term. Therefore, (B

)/2 is called the symmetric part of

, and (B

− B

)/2 is called the antisymmetric part of B

Every vector can be associated with an antisymmetric tensor, and vice versa. For

example, we can associate the vector

ω =









with an antisymmetric tensor deﬁned by

12. Eigenvalues and Eigenvectors of a Symmetric Tensor 41

R ≡





0 −ω

−ω





, (2.26)

where the two are related as

=−ε

ij k

=−

ij k

(2.27)

As a check, equation (2.27) gives R

= 0 and R

=−ε

123

=−ω

, which is in

agreement with equation (2.26). (In Chapter 3 we shall call R the “rotation” tensor

corresponding to the “vorticity” vector ω.)

A very frequently occurring operation is the doubly contracted product of a

symmetric tensor τ and any tensor B. The doubly contracted product is deﬁned as

P ≡ τ

= τ

+ A

where S and A are the symmetric and antisymmetric parts of B, given by

≡

+ B

) and A

≡

− B

Then

P = τ

+ τ

(2.28)

= τ

− τ

because S

= S

and A

=−A

= τ

− τ

because τ

= τ

− τ

interchanging dummy indices. (2.29)

Comparing the two forms of equations (2.28) and (2.29), we see that τ

= 0, so

that

+ B

The important rule we have proved is that the doubly contracted product of a symmetric

tensor τ with any tensor B equals τ times the symmetric part of B. In the process,

we have also shown that the doubly contracted product of a symmetric tensor and an

antisymmetric tensor is zero. This is analogous to the result that the deﬁnite integral

over an even (symmetric) interval of the product of a symmetric and an antisymmetric

function is zero.

12. Eigenvalues and Eigenvectors of a Symmetric Tensor

The reader is assumed to be familiar with the concepts of eigenvalues and eigenvectors

of a matrix, and only a brief review of the main results is given here. Suppose τ is a