Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

2 Introduction

not quite separable because the engineers need to understand and the physicists need

to be motivated through applications.

Fluid mechanics, like the study of any other branch of science, needs mathemat-

ical analyses as well as experimentation. The analytical approaches help in ﬁnding the

solutions to certain idealized and simpliﬁed problems, and in understanding the unity

behind apparently dissimilar phenomena. Needless to say, drastic simpliﬁcations are

frequently necessary because of the complexity of real phenomena. A good under-

standing of mathematical techniques is deﬁnitely helpful here, although it is probably

fair to say that some of the greatest theoretical contributions have come from the

people who depended rather strongly on their unusual physical intuition, some sort

of a “vision” by which they were able to distinguish between what is relevant and

what is not. Chess player, Bobby Fischer (appearing on the television program “The

Johnny Carson Show,” about 1979), once compared a good chess player and a great

one in the following manner: When a good chess player looks at a chess board, he

thinks of 20 possible moves; he analyzes all of them and picks the one that he likes.

A great chess player, on the other hand, analyzes only two or three possible moves;

his unusual intuition (part of which must have grown from experience) allows him

immediately to rule out a large number of moves without going through an apparent

logical analysis. Ludwig Prandtl, one of the founders of modern ﬂuid mechanics,

ﬁrst conceived the idea of a boundary layer based solely on physical intuition. His

knowledge of mathematics was rather limited, as his famous student von Karman

(1954, page 50) testiﬁes. Interestingly, the boundary layer technique has now become

one of the most powerful methods in applied mathematics!

As in other ﬁelds, our mathematical ability is too limited to tackle the complex

problems of real ﬂuid ﬂows. Whether we are primarily interested either in under-

standing the physics or in the applications, we must depend heavily on experimental

observations to test our analyses and develop insights into the nature of the phe-

nomenon. Fluid dynamicists cannot afford to think like pure mathematicians. The

well-known English pure mathematician G. H. Hardy once described applied math-

ematics as a form of “gloriﬁed plumbing” (G. I. Taylor, 1974). It is frightening to

imagine what Hardy would have said of experimental sciences!

This book is an introduction to ﬂuid mechanics, and is aimed at both

physicists and engineers. While the emphasis is on understanding the elementary

concepts involved, applications to the various engineering ﬁelds have been discussed

so as to motivate the reader whose main interest is to solve industrial problems. Need-

less to say, the reader will not get complete satisfaction even after reading the entire

book. It is more likely that he or she will have more questions about the nature of

ﬂuid ﬂows than before studying this book. The purpose of the book, however, will be

well served if the reader is more curious and interested in ﬂuid ﬂows.

2. Units of Measurement

For mechanical systems, the units of all physical variables can be expressed in terms

of the units of four basic variables, namely, length, mass, time, and temperature.

In this book the international system of units (Syst

eme international d’ unit

es) and

commonly referred to as SI units, will be used most of the time. The basic units

3. Solids, Liquids, and Gases 3

TABLE 1.1 SI Units

Quantity Name of unit Symbol Equivalent

Length meter m

Mass kilogram kg

Time second s

Temperature kelvin K

Frequency hertz Hz s

−1

Force newton N kg m s

−2

Pressure pascal Pa N m

−2

Energy joule J N m

Power watt W J s

−1

TABLE 1.2 Common Preﬁxes

Preﬁx Symbol Multiple

Mega M 10

Kilo k 10

Deci d 10

−1

Centi c 10

−2

Milli m 10

−3

Micro µ 10

−6

of this system are meter for length, kilogram for mass, second for time, and kelvin

for temperature. The units for other variables can be derived from these basic units.

Some of the common variables used in ﬂuid mechanics, and their SI units, are listed

in Table 1.1. Some useful conversion factors between different systems of units are

listed in Section A1 in Appendix A.

To avoid very large or very small numerical values, preﬁxes are used to indicate

multiples of the units given in Table 1.1. Some of the common preﬁxes are listed in

Table 1.2.

Strict adherence to the SI system is sometimes cumbersome and will be aban-

doned in favor of common usage where it best serves the purpose of simplifying

things. For example, temperatures will be frequently quoted in degrees Celsius (

◦

C),

which is related to kelvin (K) by the relation

◦

C = K − 273.15. However, the old

English system of units (foot, pound,

◦

F) will not be used, although engineers in the

United States are still using it.

3. Solids, Liquids, and Gases

Most substances can be described as existing in two states—solid and ﬂuid. An

element of solid has a preferred shape, to which it relaxes when the external forces

on it are withdrawn. In contrast, a ﬂuid does not have any preferred shape. Consider

a rectangular element of solid ABCD (Figure 1.1a). Under the action of a shear force

F the element assumes the shape ABC



. If the solid is perfectly elastic, it goes

back to its preferred shape ABCD when F is withdrawn. In contrast, a ﬂuid deforms

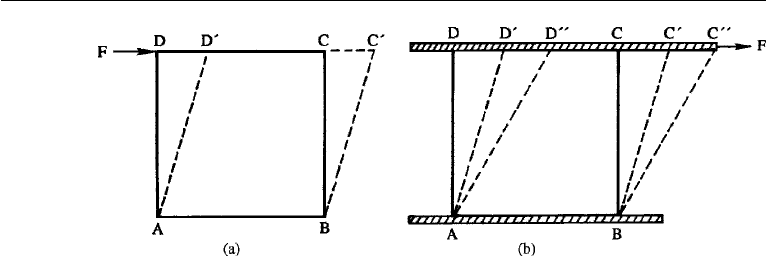
4 Introduction

Figure 1.1 Deformation of solid and ﬂuid elements: (a) solid; and (b) ﬂuid.

continuously under the action of a shear force, however small. Thus, the element of

the ﬂuid ABCD conﬁned between parallel plates (Figure 1.1b) deforms to shapes

such as ABC



and ABC



as long as the force F is maintained on the upper plate.

Therefore, we say that a ﬂuid ﬂows.

The qualiﬁcation “however small” in the forementioned description of a ﬂuid is

signiﬁcant. This is because most solids also deform continuously if the shear stress

exceeds a certain limiting value, corresponding to the “yield point” of the solid. A

solid in such a state is known as “plastic.” In fact, the distinction between solids and

ﬂuids can be hazy at times. Substances like paints, jelly, pitch, polymer solutions, and

biological substances (for example, egg white) simultaneously display the character-

istics of both solids and ﬂuids. If we say that an elastic solid has “perfect memory”

(because it always relaxes back to its preferred shape) and that an ordinary viscous

ﬂuid has zero memory, then substances like egg white can be called viscoelastic

because they have “partial memory.”

Althoughsolids andﬂuidsbehaveverydifferentlywhensubjected toshear stresses,

they behave similarly under the action of compressive normal stresses. However,

whereas a solid can support both tensile and compressive normal stresses, a ﬂuid

usuallysupportsonlycompression(pressure)stresses.(Someliquidscansupportasmall

amount of tensile stress, the amount depending on the degree of molecular cohesion.)

Fluids again may be divided into two classes, liquids and gases. A gas always

expands and occupies the entire volume of any container. In contrast, the volume of a

liquid does not change very much, so that it cannot completely ﬁll a large container;

in a gravitational ﬁeld a free surface forms that separates the liquid from its vapor.

4. Continuum Hypothesis

A ﬂuid, or any other substance for that matter, is composed of a large number of

molecules in constant motion and undergoing collisions with each other. Matter is

therefore discontinuous or discrete at microscopic scales. In principle, it is possible to

study the mechanics of a ﬂuid by studying the motion of the molecules themselves, as

is done in kinetic theory or statistical mechanics. However, we are generally interested

in the gross behavior of the ﬂuid, that is, in the average manifestation of the molecular

motion. For example, forces are exerted on the boundaries of a container due to the

constant bombardment of the molecules; the statistical average of this force per unit

5. Transport Phenomena 5

area is called pressure, a macroscopic property. So long as we are not interested in the

mechanism of the origin of pressure, we can ignore the molecular motion and think

of pressure as simply “force per unit area.”

It is thus possible to ignore the discrete molecular structure of matter and replace

it by a continuous distribution, called a continuum. For the continuum or macroscopic

approach to be valid, the size of the ﬂow system (characterized, for example, by the

size of the body around which ﬂow is taking place) must be much larger than the mean

free path of the molecules. For ordinary cases, however, this is not a great restriction,

since the mean free path is usually very small. For example, the mean free path for

standard atmospheric air is ≈5 × 10

−8

m. In special situations, however, the mean

free path of the molecules can be quite large and the continuum approach breaks

down. In the upper altitudes of the atmosphere, for example, the mean free path of

the molecules may be of the order of a meter, a kinetic theory approach is necessary

for studying the dynamics of these rareﬁed gases.

5. Transport Phenomena

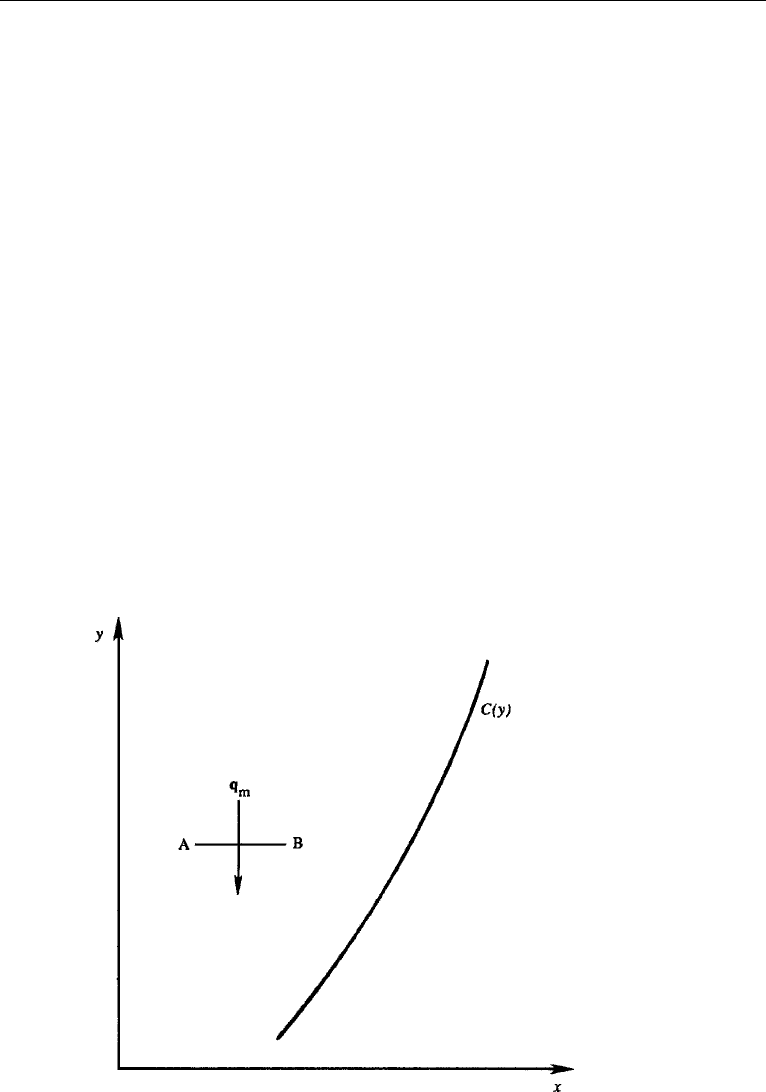
Consider a surface area AB within a mixture of two gases, say nitrogen and oxygen

(Figure 1.2), and assume that the concentration C of nitrogen (kilograms of nitrogen

per cubic meter of mixture) varies across AB. Random migration of molecules across

AB in both directions will result in a net ﬂux of nitrogen across AB, from the region

of higher C toward the region of lower C. Experiments show that, to a good approx-

imation, the ﬂux of one constituent in a mixture is proportional to its concentration

Figure 1.2 Mass ﬂux q

due to concentration variation C(y) across AB.

6 Introduction

gradient and it is given by

=−k

∇C. (1.1)

Here the vector q

is the mass ﬂux (kg m

−2

−1

) of the constituent, ∇C is the con-

centration gradient of that constituent, and k

is a constant of proportionality that

depends on the particular pair of constituents in the mixture and the thermodynamic

state. For example, k

for diffusion of nitrogen in a mixture with oxygen is different

than k

for diffusion of nitrogen in a mixture with carbon dioxide. The linear rela-

tion (1.1) for mass diffusion is generally known as Fick’s law. Relations like these

are based on empirical evidence, and are called phenomenological laws. Statistical

mechanics can sometimes be used to derive such laws, but only for simple situations.

The analogous relation for heat transport due to temperature gradient is Fourier’s

law and it is given by

q =−k∇T, (1.2)

where q is the heat ﬂux (Jm

−2

−1

), ∇T is the temperature gradient, and k is the

thermal conductivity of the material.

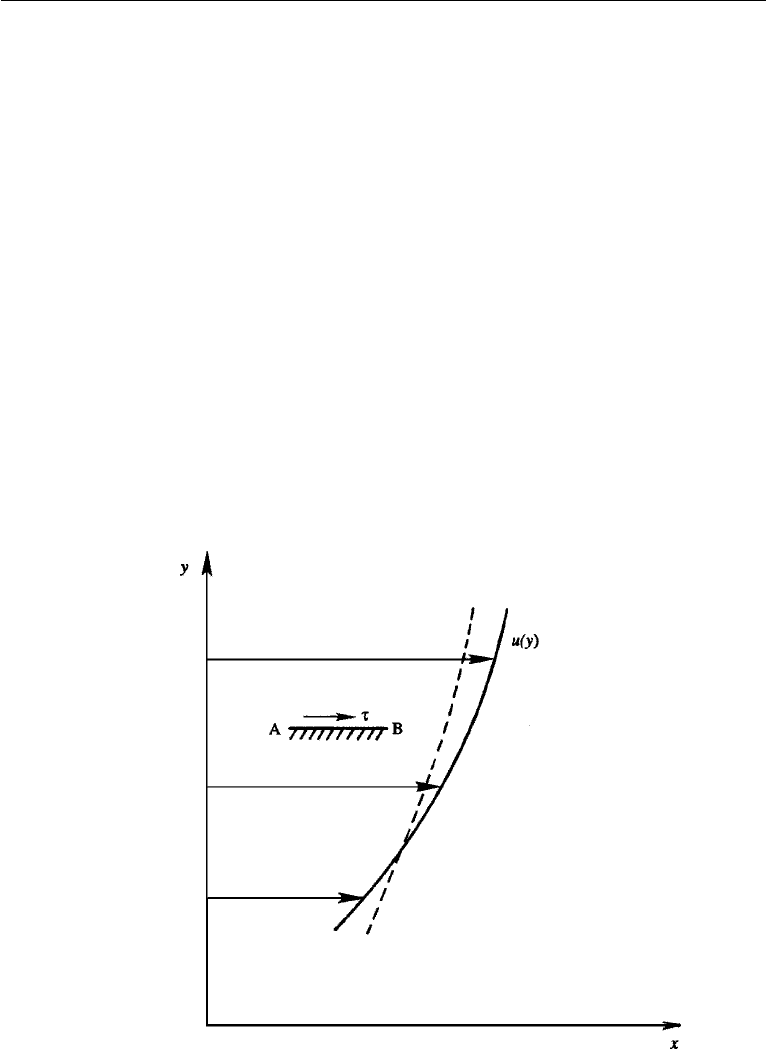
Next, consider the effect of velocity gradient du/dy (Figure 1.3). It is clear that

the macroscopic ﬂuid velocity u will tend to become uniform due to the random

Figure 1.3 Shear stress τ on surface AB. Diffusion tends to decrease velocity gradients, so that the

continuous line tends toward the dashed line.

5. Transport Phenomena 7

motion of the molecules, because of intermolecular collisions and the consequent

exchange of molecular momentum. Imagine two railroad trains traveling on parallel

tracks at different speeds, and workers shoveling coal from one train to the other. On

the average, the impact of particles of coal going from the slower to the faster train will

tend to slow down the faster train, and similarly the coal going from the faster to the

slower train will tend to speed up the latter. The net effect is a tendency to equalize the

speeds of the two trains. An analogous process takes place in the ﬂuid ﬂow problem

of Figure 1.3. The velocity distribution here tends toward the dashed line, which can

be described by saying that the x-momentum (determined by its “concentration” u)

is being transferred downward. Such a momentum ﬂux is equivalent to the existence

of a shear stress in the ﬂuid, just as the drag experienced by the two trains results

from the momentum exchange through the transfer of coal particles. The ﬂuid above

AB tends to push the ﬂuid underneath forward, whereas the ﬂuid below AB tends

to drag the upper ﬂuid backward. Experiments show that the magnitude of the shear

stress τ along a surface such as AB is, to a good approximation, related to the velocity

gradient by the linear relation

τ = µ

, (1.3)

which is called Newton’s law of friction. Here the constant of proportionality µ

(whose unit is kg m

−1

) is known as the dynamic viscosity, which is a strong

function of temperature T . For ideal gases the random thermal speed is roughly

proportional to

√

T ; the momentum transport, and consequently µ, also vary approx-

imately as

√

T . For liquids, on the other hand, the shear stress is caused more by the

intermolecular cohesive forces than by the thermal motion of the molecules. These

cohesive forces, and consequently µ for a liquid, decrease with temperature.

Although the shear stress is proportional to µ, we will see in Chapter 4 that the

tendency of a ﬂuid to diffuse velocity gradients is determined by the quantity

ν ≡

, (1.4)

where ρ is the density (kg/m

) of the ﬂuid. The unit of ν is m

/s, which does not

involve the unit of mass. Consequently, ν is frequently called the kinematic viscosity.

Two points should be noticed in the linear transport laws equations (1.1), (1.2),

and (1.3). First, only the ﬁrst derivative of some generalized “concentration” C appears

on the right-hand side. This is because the transport is carried out by molecular pro-

cesses, in which the length scales (say, the mean free path) are too small to feel the cur-

vature of the C-proﬁle. Second, the nonlinear terms involving higher powers of ∇C do

not appear. Although this is only expected for small magnitudes of ∇C, experiments

show that such linear relations are very accurate for most practical values of ∇C.

It should be noted here that we have written the transport law for momentum

far less precisely than the transport laws for mass and heat. This is because we

have not developed the language to write this law with precision. The transported

quantities in (1.1) and (1.2) are scalars (namely, mass and heat, respectively), and the

8 Introduction

corresponding ﬂuxes are vectors. In contrast, the transported quantity in (1.3) is itself

a vector, and the corresponding ﬂux is a “tensor.” The precise form of (1.3) will be

presented in Chapter 4, after the concept of tensors is explained in Chapter 2. For now,

we have avoided complications by writing the transport law for only one component

of momentum, using scalar notation.

6. Surface Tension

A density discontinuity exists whenever two immiscible ﬂuids are in contact, for

example at the interface between water and air. The interface in this case is found

to behave as if it were under tension. Such an interface behaves like a stretched

membrane, such as the surface of a balloon or of a soap bubble. This is why drops of

liquid in air or gas bubbles in water tend to be spherical in shape. The origin of such

tension in an interface is due to the intermolecular attractive forces. Imagine a liquid

drop surrounded by a gas. Near the interface, all the liquid molecules are trying to

pull the molecules on the interface inward. The net effect of these attractive forces is

for the interface to contract. The magnitude of the tensile force per unit length of a

line on the interface is called surface tension σ , which has the unit N/m. The value

of σ depends on the pair of ﬂuids in contact and the temperature.

An important consequence of surface tension is that it gives rise to a pressure

jump across the interface whenever it is curved. Consider a spherical interface having

a radius of curvature R (Figure 1.4a). If p

and p

are the pressures on the two sides

of the interface, then a force balance gives

σ(2πR) = (p

− p

)πR

from which the pressure jump is found to be

− p

2σ

, (1.5)

Figure 1.4 (a) Section of a spherical droplet, showing surface tension forces. (b) An interface with radii

of curvatures R

and R

along two orthogonal directions.

7. Fluid Statics 9

showing that the pressure on the concave side is higher. The pressure jump, however,

is small unless R is quite small.

Equation (1.5) holds only if the surface is spherical. The curvature of a general

surface can be speciﬁed by the radii of curvature along two orthogonal directions,

say, R

and R

(Figure 1.4b). A similar analysis shows that the pressure jump across

the interface is given by

− p

= σ





which agrees with equation (1.5) if R

= R

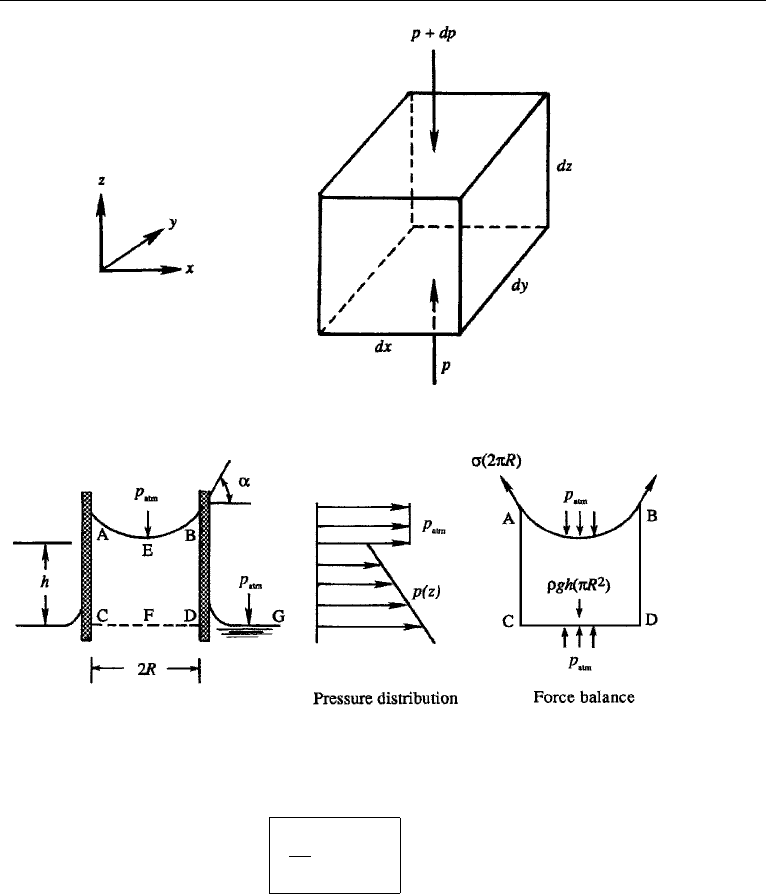
It is well known that the free surface of a liquid in a narrow tube rises above

the surrounding level due to the inﬂuence of surface tension. This is demonstrated in

Example 1.1. Narrow tubes are called capillary tubes (from Latin capillus, meaning

“hair”). Because of this phenomenon the whole group of phenomena that arise from

surface tension effects is called capillarity. A more complete discussion of surface

tension is presented at the end of Chapter 4 (Section 19) as part of an expanded section

on boundary conditions.

7. Fluid Statics

The magnitude of the force per unit area in a static ﬂuid is called the pressure. (More

care is needed to deﬁne the pressure in a moving medium, and this will be done in

Chapter 4.) Sometimes the ordinary pressure is called the absolute pressure, in order

to distinguish it from the gauge pressure, which is deﬁned as the absolute pressure

minus the atmospheric pressure:

gauge

= p − p

atm

The value of the atmospheric pressure is

atm

= 101.3kPa = 1.013 bar,

where 1 bar = 10

Pa. The atmospheric pressure is therefore approximately 1 bar.

In a ﬂuid at rest, the tangential viscous stresses are absent and the only force

between adjacent surfaces is normal to the surface. We shall now demonstrate that

in such a case the surface force per unit area (“pressure”) is equal in all directions.

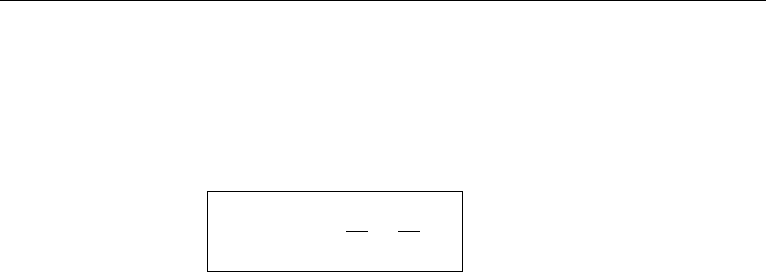
Consider a small triangular volume of ﬂuid (Figure 1.5) of unit thickness normal to

the paper, and let p

, and p

be the pressures on the three faces. The z-axis is

taken vertically upward. The only forces acting on the element are the pressure forces

normal to the faces and the weight of the element. Because there is no acceleration

of the element in the x direction, a balance of forces in that direction gives

ds)sin θ − p

dz = 0.

10 Introduction

Figure 1.5 Demonstration that p

= p

in a static ﬂuid.

Because dz = ds sin θ, the foregoing gives p

= p

. A balance of forces in the

vertical direction gives

−(p

ds)cos θ +p

dx −

ρg dx dz = 0.

As ds cos θ = dx, this gives

− p

−

ρg dz = 0.

As the triangular element is shrunk to a point, the gravity force term drops out, giving

= p

. Thus, at a point in a static ﬂuid, we have

= p

, (1.6)

so that the force per unit area is independent of the angular orientation of the surface.

The pressure is therefore a scalar quantity.

We now proceed to determine the spatial distribution of pressure in a static ﬂuid.

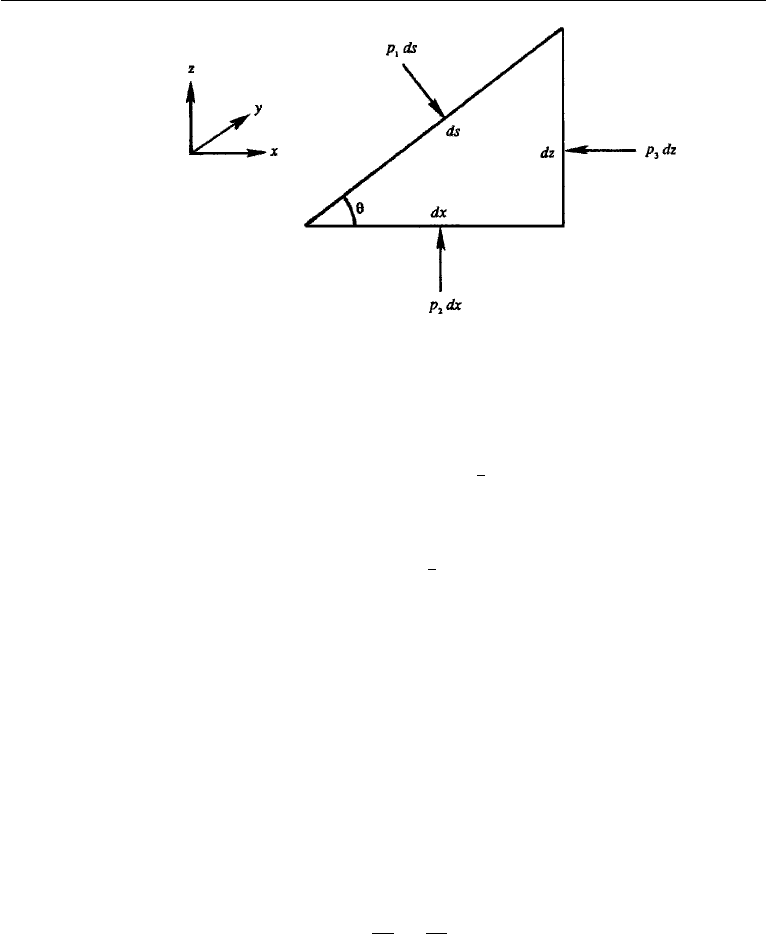
Consider an inﬁnitesimal cube of sides dx, dy, and dz, with the z-axis vertically

upward (Figure 1.6). A balance of forces in the x direction shows that the pressures

on the two sides perpendicular to the x-axis are equal. A similar result holds in the

y direction, so that

∂p

∂x

∂p

∂y

= 0. (1.7)

This fact is expressed by Pascal’s law, which states that all points in a resting ﬂuid

medium (and connected by the same ﬂuid) are at the same pressure if they are at the

same depth. For example, the pressure at points F and G in Figure 1.7 are the same.

A vertical equilibrium of the element in Figure 1.6 requires that

pdxdy− (p + dp) dx dy − ρgdx dy dz = 0,

7. Fluid Statics 11

Figure 1.6 Fluid element at rest.

Figure 1.7 Rise of a liquid in a narrow tube (Example 1.1).

which simpliﬁes to

=−ρg.

(1.8)

This shows that the pressure in a static ﬂuid decreases with height. For a ﬂuid of

uniform density, equation (1.8) can be integrated to give

p = p

− ρgz, (1.9)

where p

is the pressure at z = 0. Equation (1.9) is the well-known result of hydrostat-

ics, and shows that the pressure in a liquid decreases linearly with height. It implies

that the pressure rise at a depth h below the free surface of a liquid is equal to ρgh,

which is the weight of a column of liquid of height h and unit cross section.