Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

12 Introduction

Example 1.1. With reference to Figure 1.7, show that the rise of a liquid in a narrow

tube of radius R is given by

h =

2σ sin α

ρgR

where σ is the surface tension and α is the “contact” angle.

Solution. Since the free surface is concave upward and exposed to the atmo-

sphere, the pressure just below the interface at point E is below atmospheric. The

pressure then increases linearly along EF. At F the pressure again equals the atmo-

spheric pressure, since F is at the same level as G where the pressure is atmospheric.

The pressure forces on faces AB and CD therefore balance each other. Vertical equi-

librium of the element ABCD then requires that the weight of the element balances

the vertical component of the surface tension force, so that

σ(2πR)sin α = ρgh(πR

which gives the required result.

8. Classical Thermodynamics

Classical thermodynamics is the study of equilibrium states of matter, in which the

properties are assumed uniform in space and time. The reader is assumed to be familiar

with the basic concepts of this subject. Here we give a review of the main ideas and

the most commonly used relations in this book.

A thermodynamic system is a quantity of matter separated from the surroundings

by a ﬂexible boundary through which the system exchanges heat and work, but no

mass. A system in the equilibrium state is free of currents, such as those generated

by stirring a ﬂuid or by sudden heating. After a change has taken place, the currents

die out and the system returns to equilibrium conditions, when the properties of the

system (such as pressure and temperature) can once again be deﬁned.

This deﬁnition, however, is not possible in ﬂuid ﬂows, and the question arises as

to whether the relations derived in classical thermodynamics are applicable to ﬂuids

in constant motion. Experiments show that the results of classical thermodynamics

do hold in most ﬂuid ﬂows if the changes along the motion are slow compared to a

relaxation time. The relaxation time is deﬁned as the time taken by the material to

adjust to a new state, and the material undergoes this adjustment through molecular

collisions. The relaxation time is very small under ordinary conditions, since only

a few molecular collisions are needed for the adjustment. The relations of classical

thermodynamics are therefore applicable to most ﬂuid ﬂows.

The basic laws of classical thermodynamics are empirical, and cannot be proved.

Another way of viewing this is to say that these principles are so basic that they

cannot be derived from anything more basic. They essentially establish certain basic

deﬁnitions, upon which the subject is built. The ﬁrst law of thermodynamics can be

regarded as a principle that deﬁnes the internal energy of a system, and the second

law can be regarded as the principle that deﬁnes the entropy of a system.

8. Classical Thermodynamics 13

First Law of Thermodynamics

The ﬁrst law of thermodynamics states that the energy of a system is conserved. It

states that

Q + W = e, (1.10)

where Q is the heat added to the system, W is the work done on the system, and e

is the increase of internal energy of the system. All quantities in equation (1.10) may

be regarded as those referring to unit mass of the system. (In thermodynamics texts it

is customary to denote quantities per unit mass by lowercase letters, and those for the

entire system by uppercase letters. This will not be done here.) The internal energy

(also called “thermal energy”) is a manifestation of the random molecular motion of

the constituents. In ﬂuid ﬂows, the kinetic energy of the macroscopic motion has to be

included in the term e in equation (1.10) in order that the principle of conservation of

energy is satisﬁed. For developing the relations of classical thermodynamics, however,

we shall only include the “thermal energy” in the term e.

It is important to realize the difference between heat and internal energy. Heat and

work are forms of energy in transition, which appear at the boundary of the system

and are not contained within the matter. In contrast, the internal energy resides within

the matter. If two equilibrium states 1 and 2 of a system are known, then Q and W

depend on the process or path followed by the system in going from state 1 to state 2.

The change e = e

− e

, in contrast, does not depend on the path. In short, e is a

thermodynamic property and is a function of the thermodynamic state of the system.

Thermodynamic properties are called state functions, in contrast to heat and work,

which are path functions.

Frictionless quasi-static processes, carried out at an extremely slow rate so that

the system is at all times in equilibrium with the surroundings, are called reversible

processes. The most common type of reversible work in ﬂuid ﬂows is by the expansion

or contraction of the boundaries of the ﬂuid element. Let v = 1/ρ be the speciﬁc

volume, that is, the volume per unit mass. Then the work done by the body per unit

mass in an inﬁnitesimal reversible process is −pdv, where dv is the increase of v.

The ﬁrst law (equation (1.10)) for a reversible process then becomes

de = dQ − pdv, (1.11)

provided that Q is also reversible.

Note that irreversible forms of work, such as that done by turning a paddle wheel,

are excluded from equation (1.11).

Equations of State

In simple systems composed of a single component only, the speciﬁcation of two

independent properties completely determines the state of the system. We can write

relations such as

p = p(v, T ) (thermal equation of state),

e = e(p, T ) (caloric equation of state).

(1.12)

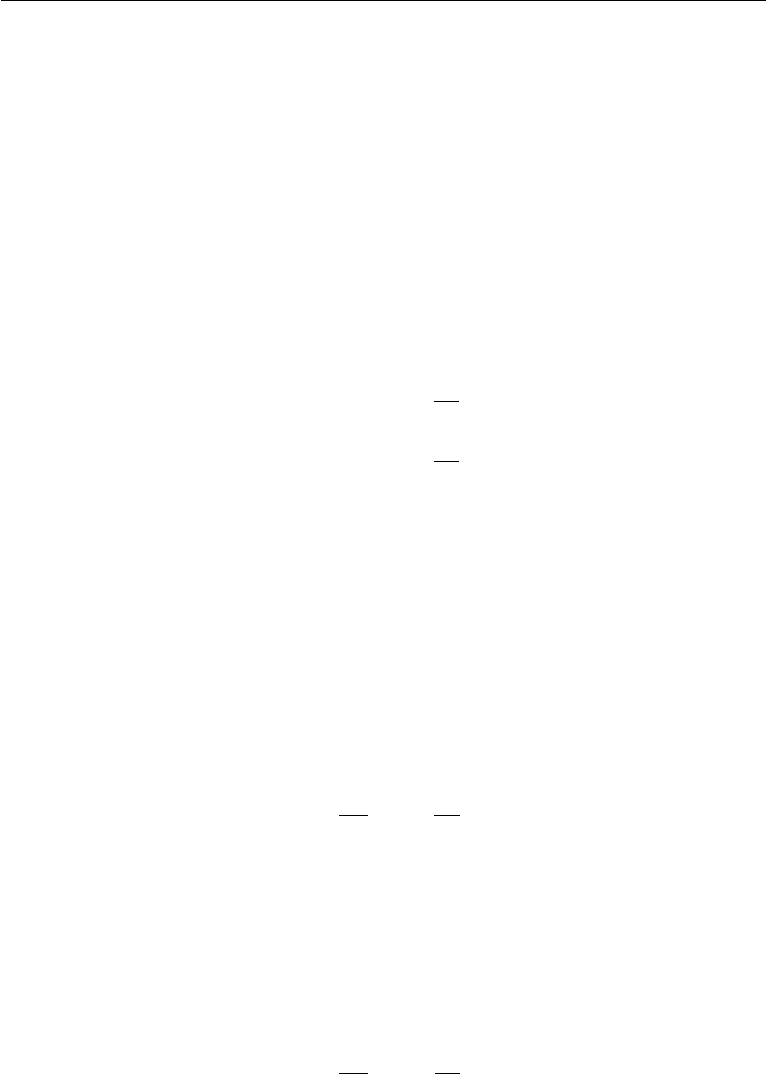
14 Introduction

Such relations are called equations of state. For more complicated systems composed

of more than one component, the speciﬁcation of two properties is not enough to

completely determine the state. For example, for sea water containing dissolved salt,

the density is a function of the three variables, salinity, temperature, and pressure.

Speciﬁc Heats

Before we deﬁne the speciﬁc heats of a substance, we deﬁne a thermodynamic prop-

erty called enthalpy as

h ≡ e + pv. (1.13)

This property will be quite useful in our study of compressible ﬂuid ﬂows.

For single-component systems, the speciﬁc heats at constant pressure and con-

stant volume are deﬁned as

≡



∂h

∂T



, (1.14)

≡



∂e

∂T



. (1.15)

Here, equation (1.14) means that we regard h as a function of p and T , and ﬁnd the

partial derivative of h with respect to T , keeping p constant. Equation (1.15) has an

analogous interpretation. It is important to note that the speciﬁc heats as deﬁned are

thermodynamic properties, because they are deﬁned in terms of other properties of

the system. That is, we can determine C

and C

when two other properties of the

system (say, p and T ) are given.

For certain processes common in ﬂuid ﬂows, the heat exchange can be related

to the speciﬁc heats. Consider a reversible process in which the work done is given

by pdv, so that the ﬁrst law of thermodynamics has the form of equation (1.11).

Dividing by the change of temperature, it follows that the heat transferred per unit

mass per unit temperature change in a constant volume process is







∂e

∂T



= C

This shows that C

dT represents the heat transfer per unit mass in a reversible

constant volume process, in which the only type of work done is of the pdv type.

It is misleading to deﬁne C

= (dQ/dT )

without any restrictions imposed, as the

temperature of a constant-volume system can increase without heat transfer, say, by

turning a paddle wheel.

In a similar manner, the heat transferred at constant pressure during a reversible

process is given by







∂h

∂T



= C

8. Classical Thermodynamics 15

Second Law of Thermodynamics

The second law of thermodynamics imposes restriction on the direction in which

real processes can proceed. Its implications are discussed in Chapter 4. Some conse-

quences of this law are the following:

(i) There must exist a thermodynamic property S, known as entropy, whose

change between states 1 and 2 is given by

− S



rev

, (1.16)

where the integral is taken along any reversible process between the two states.

(ii) For an arbitrary process between 1 and 2, the entropy change is

− S





(Clausius-Duhem),

which states that the entropy of an isolated system (dQ = 0) can only increase.

Such increases are caused by frictional and mixing phenomena.

(iii) Molecular transport coefﬁcients such as viscosity µ and thermal conductivity

k must be positive. Otherwise, spontaneous “unmixing” would occur and lead

to a decrease of entropy of an isolated system.

TdSRelations

Two common relations are useful in calculating the entropy changes during a process.

For a reversible process, the entropy change is given by

TdS = dQ. (1.17)

On substituting into (1.11), we obtain

TdS = de + pdv

TdS = dh − vdp

(Gibbs), (1.18)

where the second form is obtained by using dh = d(e + pv) = de + pdv +

vdp. It is interesting that the “TdSrelations” in equations (1.18) are also valid for

irreversible (frictional) processes, although the relations (1.11) and (1.17), from which

equations (1.18) is derived, are true for reversible processes only. This is because

equations (1.18) are relations between thermodynamic state functions alone and are

therefore true for any process. The association of TdSwith heat and −pdv with

work does not hold for irreversible processes. Consider paddle wheel work done at

constant volume so that de = TdSis the element of work done.

16 Introduction

Speed of Sound

In a compressible medium, inﬁnitesimal changes in density or pressure propagate

through the medium at a ﬁnite speed. In Chapter 16, we shall prove that the square

of this speed is given by



∂p

∂ρ



, (1.19)

where the subscript “s” signiﬁes that the derivative is taken at constant entropy. As

sound is composed of small density perturbations, it also propagates at speed c.For

incompressible ﬂuids ρ is independent of p, and therefore c =∞.

Thermal Expansion Coefﬁcient

In a system whose density is a function of temperature, we deﬁne the thermal expan-

sion coefﬁcient

α ≡−



∂ρ

∂T



, (1.20)

where the subscript “p” signiﬁes that the partial derivative is taken at constant pressure.

The expansion coefﬁcient will appear frequently in our studies of nonisothermal

systems.

9. Perfect Gas

A relation deﬁning one state function of a gas in terms of two others is called an

equation of state. A perfect gas is deﬁned as one that obeys the thermal equation of

state

p = ρRT,

(1.21)

where p is the pressure, ρ is the density, T is the absolute temperature, and R is the

gas constant. The value of the gas constant depends on the molecular mass m of the

gas according to

R =

, (1.22)

where

= 8314.36 J kmol

−1

is the universal gas constant. For example, the molecular mass for dry air is

m = 28.966 kg/kmol, for which equation (1.22) gives

R = 287 J kg

−1

for dry air.

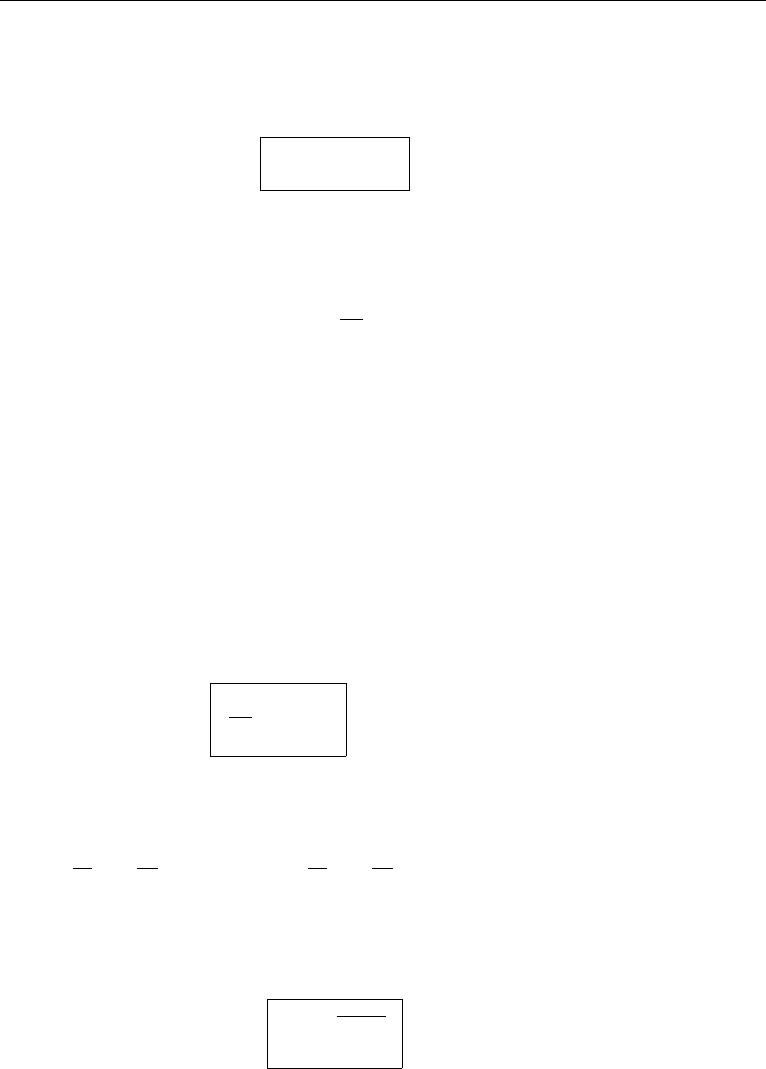
9. Perfect Gas 17

Equation (1.21) can be derived from the kinetic theory of gases if the attractive

forces between the molecules are negligible. At ordinary temperatures and pressures

most gases can be taken as perfect.

The gas constant is related to the speciﬁc heats of the gas through the relation

R = C

− C

, (1.23)

where C

is the speciﬁc heat at constant pressure and C

is the speciﬁc heat at constant

volume. In general, C

and C

of a gas, including those of a perfect gas, increase with

temperature. The ratio of speciﬁc heats of a gas

γ ≡

, (1.24)

is an important quantity. For air at ordinary temperatures, γ = 1.4 and C p =

1005 J kg

−1

It can be shown that assertion (1.21) is equivalent to

e = e(T )

h = h(T )

and conversely, so that the internal energy and enthalpy of a perfect gas can only be

functions of temperature alone. See Exercise 7.

A process is called adiabatic if it takes place without the addition of heat. A

process is called isentropic if it is adiabatic and frictionless, for then the entropy of

the ﬂuid does not change. From equation (1.18) it is easy to show that the isentropic

ﬂow of a perfect gas with constant speciﬁc heats obeys the relation

= const. (isentropic) (1.25)

Using the equation of state p = ρRT , it follows that the temperature and density

change during an isentropic process from state 1 to state 2 according to





(γ −1)/γ

and





1/γ

(isentropic) (1.26)

See Exercise 8. For a perfect gas, simple expressions can be found for several

useful thermodynamic properties such as the speed of sound and the thermal expansion

coefﬁcient. Using the equation of state p = ρRT , the speed of sound (1.19) becomes

c =



γRT, (1.27)

where equation (1.25) has been used. This shows that the speed of sound increases

as the square root of the temperature. Likewise, the use of p = ρRT shows that the

18 Introduction

thermal expansion coefﬁcient (1.20) is

α =

(1.28)

10. Static Equilibrium of a Compressible Medium

In an incompressible ﬂuid in which the density is not a function of pressure, there is

a simple criterion for determining the stability of the medium in the static state. The

criterion is that the medium is stable if the density decreases upward, for then a particle

displaced upward would ﬁnd itself at a level where the density of the surrounding

ﬂuid is lower, and so the particle would be forced back toward its original level. In

the opposite case in which the density increases upward, a displaced particle would

continue to move farther away from its original position, resulting in instability. The

medium is in neutral equilibrium if the density is uniform.

For a compressible medium the preceding criterion for determining the stability

does not hold. We shall now show that in this case it is not the density but the entropy

that is constant with height in the neutral state. For simplicity we shall consider the

case of an atmosphere that obeys the equation of state for a perfect gas. The pressure

decreases with height according to

=−ρg.

A particle displaced upward would expand adiabatically because of the decrease of

the pressure with height. Its original density ρ

and original temperature T

would

therefore decrease to ρ and T according to the isentropic relations





(γ −1)/γ

and





1/γ

, (1.29)

where γ = C

, and the subscript 0 denotes the original state at some height z

where p

>p(Figure 1.8). It is clear that the displaced particle would be forced back

toward the original level if the new density is larger than that of the surrounding air

at the new level. Now if the properties of the surrounding air also happen to vary

with height in such a way that the entropy is uniform with height, then the displaced

particle would constantly ﬁnd itself in a region where the density is the same as that

of itself. Therefore, a neutral atmosphere is one in which p, ρ, and T decrease in

such a way that the entropy is constant with height. A neutrally stable atmosphere is

therefore also called an isentropic or adiabatic atmosphere. It follows that a statically

stable atmosphere is one in which the density decreases with height faster than in an

adiabatic atmosphere.

10. Static Equilibrium of a Compressible Medium 19

Figure 1.8 Adiabatic expansion of a ﬂuid particle displaced upward in a compressible medium.

It is easy to determine the rate of decrease of temperature in an adiabatic atmo-

sphere. Taking the logarithm of equation (1.29), we obtain

ln T

− ln T

γ − 1

[ln p

− ln p

where we are using the subscript “a” to denote an adiabatic atmosphere. A differen-

tiation with respect to z gives

γ − 1

Using the perfect gas law p = ρRT , C

− C

= R, and the hydrostatic rule

dp/dz =−ρg, we obtain

≡ 

=−

(1.30)

where  ≡ dT /dz is the temperature gradient; 

=−g/C

is called the adiabatic

temperature gradient and is the largest rate at which the temperature can decrease

with height without causing instability. For air at normal temperatures and pressures,

the temperature of a neutral atmosphere decreases with height at the rate of g/C



◦

C/km. Meteorologists call vertical temperature gradients the “lapse rate,” so that

in their terminology the adiabatic lapse rate is 10

◦

C/km.

Figure 1.9a shows a typical distribution of temperature in the atmosphere. The

lower part has been drawn with a slope nearly equal to the adiabatic temperature gra-

dient because the mixing processes near the ground tend to form a neutral atmosphere,

with its entropy “well mixed” (that is, uniform) with height. Observations show that

the neutral atmosphere is “capped” by a layer in which the temperature increases with

height, signifying a very stable situation. Meteorologists call this an inversion, because

the temperature gradient changes sign here. Much of the atmospheric turbulence and

mixing processes cannot penetrate this very stable layer. Above this inversion layer the

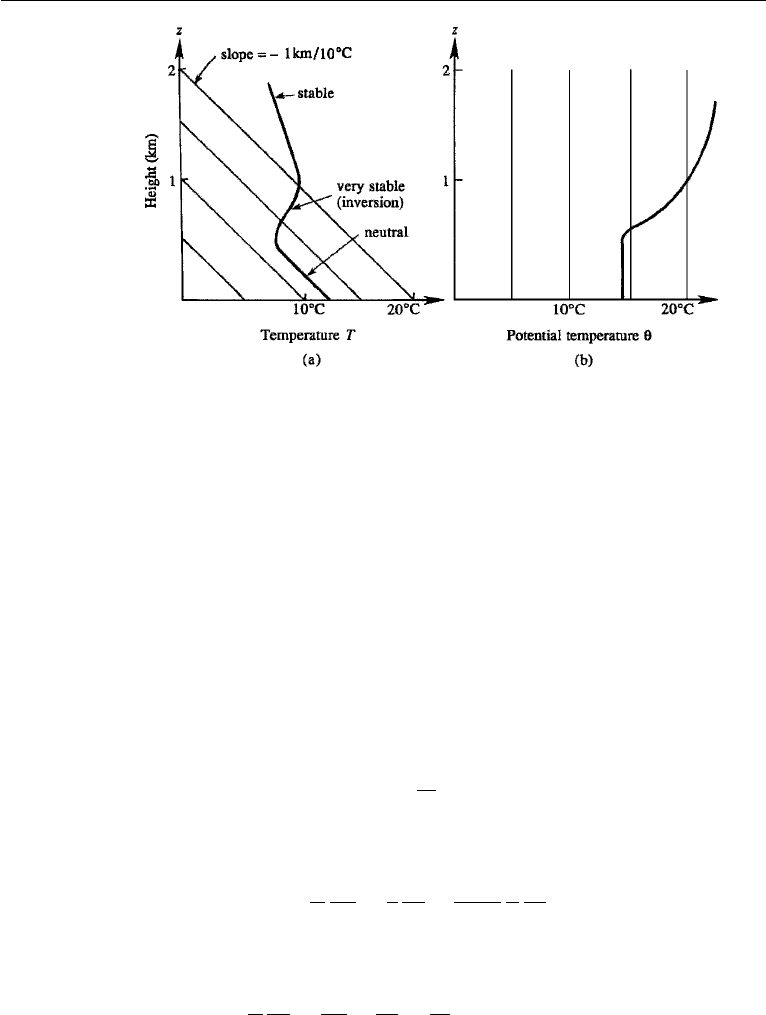
20 Introduction

Figure 1.9 Vertical variation of the (a) actual and (b) potential temperature in the atmosphere. Thin

straight lines represent temperatures for a neutral atmosphere.

temperature decreases again, but less rapidly than near the ground, which corresponds

to stability. It is clear that an isothermal atmosphere (a vertical line in Figure 1.9a) is

quite stable.

Potential Temperature and Density

The foregoing discussion of static stability of a compressible atmosphere can be

expressed in terms of the concept of potential temperature, which is generally denoted

by θ. Suppose the pressure and temperature of a ﬂuid particle at a certain height are

p and T . Now if we take the particle adiabatically to a standard pressure p

(say,

the sea level pressure, nearly equal to 100 kPa), then the temperature θ attained by

the particle is called its potential temperature. Using equation (1.26), it follows that the

actual temperature T and the potential temperature θ are related by

T = θ





(γ −1)/γ

. (1.31)

Taking the logarithm and differentiating, we obtain

dθ

γ − 1

Substituting dp/dz =−ρg and p = ρRT , we obtain

dθ

(T − T

) =  − 

. (1.32)

Now if the temperature decreases at a rate  = 

, then the potential temperature θ

(and therefore the entropy) is uniform with height. It follows that the stability of the

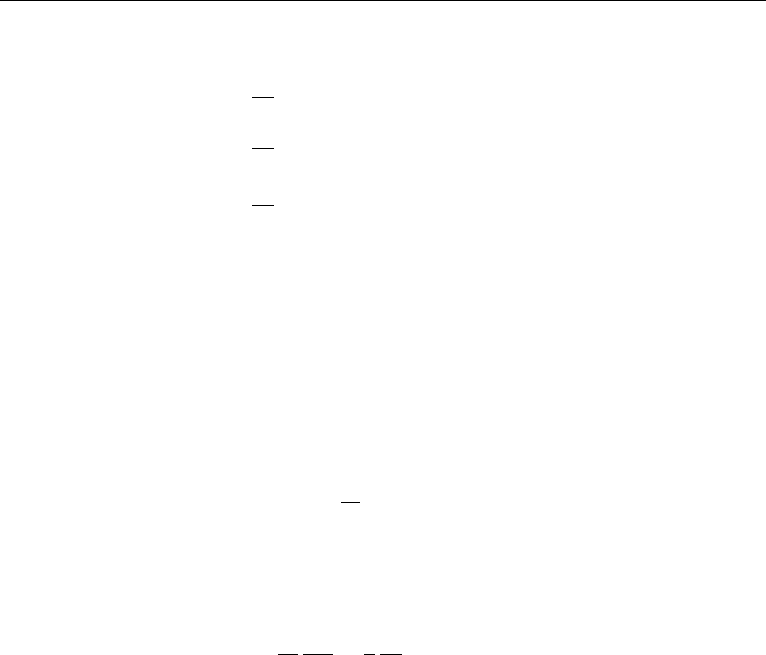
10. Static Equilibrium of a Compressible Medium 21

atmosphere is determined according to

dθ

> 0 (stable),

dθ

= 0 (neutral), (1.33)

dθ

< 0 (unstable).

This is shown in Figure 1.9b. It is the gradient of potential temperature that determines

the stability of a column of gas, not the gradient of the actual temperature. However,

the difference between the two is negligible for laboratory-scale phenomena. For

example, over a height of 10 cm the compressibility effects result in a decrease of

temperature in the air by only 10 cm × (10

◦

C/km) = 10

−3 ◦

Instead of using the potential temperature, one can use the concept of potential

density ρ

, deﬁned as the density attained by a ﬂuid particle if taken isentropically to

a standard pressure p

. Using equation (1.26), the actual and potential densities are

related by

ρ = ρ





1/γ

. (1.34)

Multiplying equations (1.31) and (1.34), and using p = ρRT, we obtain

θρ

= p

/R = const. Taking the logarithm and differentiating, we obtain

−

dρ

dθ

. (1.35)

The medium is stable, neutral, or unstable depending upon whether dρ

/dz is nega-

tive, zero, or positive, respectively.

Compressibility effects are also important in the deep ocean. In the ocean the

density depends not only on the temperature and pressure, but also on the salinity,

deﬁned as kilograms of salt per kilogram of water. (The salinity of sea water is ≈3%.)

Here, one deﬁnes the potential density as the density attained if a particle is taken to

a reference pressure isentropically and at constant salinity. The potential density thus

deﬁned must decrease with height in stable conditions. Oceanographers automatically

account for the compressibility of sea water by converting their density measurements

at any depth to the sea level pressure, which serves as the reference pressure.

From (1.32), the temperature of a dry neutrally stable atmosphere decreases

upward at a rate dT

/dz =−g/C

due to the decrease of pressure with height and

the compressibility of the medium. Static stability of the atmosphere is determined

by whether the actual temperature gradient dT /dz is slower or faster than dT

/dz.To

determine the static stability of the ocean, it is more convenient to formulate the crite-

rion in terms of density. The plan is to compare the density gradient of the actual static

state with that of a neutrally stable reference state (denoted here by the subscript “a”).