Cohen I.M., Kundu P.K. Fluid Mechanics
Подождите немного. Документ загружается.

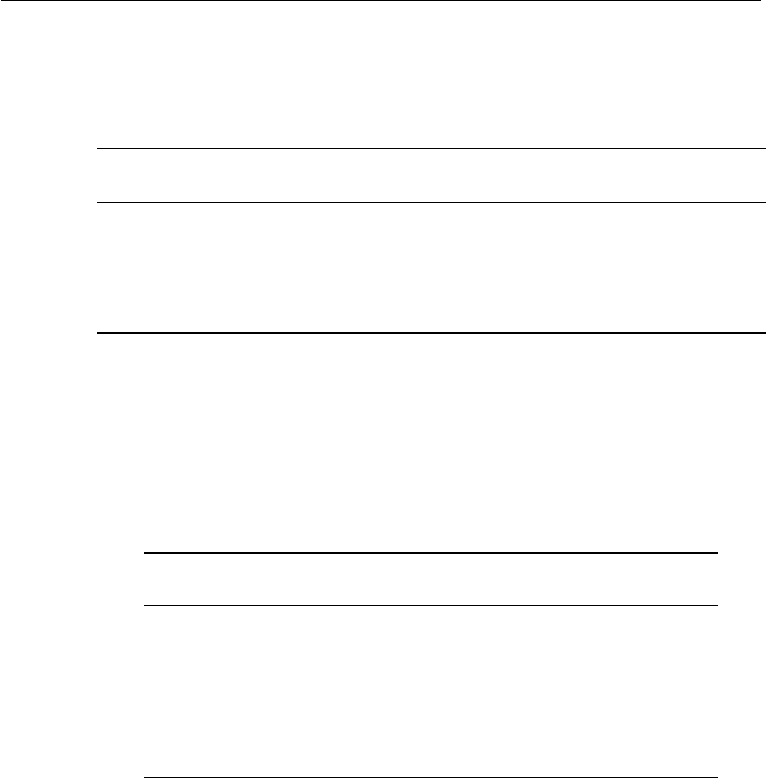
842 Appendix A: Some Properties of Common Fluids
A2. Properties of Pure Water at Atmospheric Pressure
Here, ρ = density, α = coefficient of thermal expansion, µ = shear viscosity,
ν = kinematic viscosity = µ/ρ, κ = thermal diffusivity = k/(ρC
p
),[k is first
defined on p.6] Pr = Prandtl number, and 1.0 × 10
−n
is written as 1.0E − n
Tρ α µ ν κ C
p
Pr
◦
Ckg/m
3
K
−1
kg m
−1
s
−1
m
2
/sm
2
/sJkg
−1
K
−1
ν/κ
0 1000 −0.6E − 41.787E − 31.787E − 61.33E −7 4217 13.4
10 1000 +0.9E − 41.307E − 31.307E − 61.38E −7 4192 9.5
20 997 2.1E − 41.002E − 31.005E − 61.42E −7 4182 7.1
30 995 3.0E − 40.799E − 30.802E − 61.46E − 7 4178 5.5
40 992 3.8E − 40.653E − 30.658E − 61.52E −7 4178 4.3
50 988 4.5E − 40.548E − 30.555E − 61.58E −7 4180 3.5
Latent heat of vaporization at 100
◦
C = 2.257 × 10
6
J/kg.
Latent heat of melting of ice at 0
◦
C = 0 .334 × 10
6
J/kg.
Density of ice = 920 kg/m
3
.
Surface tension between water and air at 20
◦
C = 0 .0728 N/m.
Sound speed at 25
◦
C 1500 m/s.
A3. Properties of Dry Air at Atmospheric Pressure
Tρ µ ν κ Pr
◦
Ckg/m
3
kg m
−1
s
−1
m
2
/sm
2
/s ν/κ
0 1.293 1.71E − 51.33E − 51.84E − 5 0.72
10 1.247 1.76E − 51.41E − 51.96E − 5 0.72
20 1.200 1.81E − 51.50E − 52.08E − 5 0.72
30 1.165 1.86E − 51.60E − 52.25E − 5 0.71
40 1.127 1.87E − 51.66E − 52.38E − 5 0.71
60 1.060 1.97E − 51.86E − 52.65E − 5 0.71
80 1.000 2.07E − 52.07E −52.99E − 5 0.70
100 0.946 2.17E − 52.29E −53.28E − 5 0.70
At 20
◦
C and 1 atm,
C
p
= 1012 J kg
−1
K
−1
C
v
= 718 J kg
−1
K
−1
γ = 1.4
α = 3.38 × 10
−3
K
−1
c = 340.6m/s (velocity of sound)
Constants for dry air :
Gas constant R = 287.04 J kg
−1
K
−1
Molecular mass m = 28.966 kg/kmol

A4. Properties of Standard Atmosphere 843
A4. Properties of Standard Atmosphere
The following average values are accepted by international agreement. Here, z is the
height above sea level.
z Tpρ
km
◦
CkPakg/m
3
0 15.0 101.3 1.225
0.5 11.5 95.5 1.168
1 8.5 89.9 1.112
2 2.0 79.5 1.007
3 −4.5 70.1 0.909
4 −11.0 61.6 0.819
5 −17.5 54.0 0.736
6 −24.0 47.2 0.660
8 −37.0 35.6 0.525
10 −50.0 26.4 0.413
12 −56.5 19.3 0.311
14 −56.5 14.1 0.226
16 −56.5 10.3 0.165
18 −56.5 7.5 0.120
20 −56.5 5.5 0.088
This page intentionally left blank

Appendix B
Curvilinear Coordinates
B1. Cylindrical Polar Coordinates . . 845
B2. Plane Polar Coordinates........ 847
B3. Spherical Polar Coordinates .... 847
B1. Cylindrical Polar Coordinates
The coordinates are (R,θ,x), where θ is the azimuthal angle (see Figure 3.1b, where
ϕ is used instead of θ). The equations are presented assuming ψ is a scalar, and
u = i
R
u
R
+ i
θ
u
θ
+ i
x
u
x
,
where i
R
, i
θ
, and i
x
are the local unit vectors at a point.
Gradient of a scalar
∇ψ = i
R
∂ψ
∂R
+
i
θ
R
∂ψ
∂θ
+ i
x
∂ψ
∂x
.
Laplacian of a scalar
∇
2
ψ =
1
R
∂
∂R
R
∂ψ
∂R
+
1
R
2
∂
2
ψ
∂θ
2
+
∂
2
ψ
∂x
2
.
Divergence of a vector
∇ · u =
1
R
∂(Ru
R
)
∂R
+
1
R
∂u
θ
∂θ
+
∂u
x
∂x
.
Curl of a vector
∇ × u = i
R
1
R
∂u
x
∂θ
−
∂u
θ
∂x
+ i
θ
∂u
R
∂x
−
∂u
x
∂R
+ i
x
1
R
∂(Ru
θ
)
∂R
−
1
R
∂u
R
∂θ
.
Laplacian of a vector
∇
2
u = i
R
∇
2
u
R
−
u
R
R
2
−
2
R
2
∂u
θ
∂θ
+ i
θ
∇
2
u
θ
+
2
R
2
∂u
R
∂θ
−
u
θ
R
2
+ i
x
∇
2
u
x
.
845
©2010 Elsevier Inc. All rights reserved.
DOI: 10.1016/B978-0-12-381399-2.50019-8

846 Appendix B: Curvilinear Coordinates
Strain rate and viscous stress (for incompressible form σ
ij
= 2µe
ij
)
e
RR
=
∂u
R
∂R
=
1
2µ
σ
RR
,
e
θθ
=
1
R
∂u
θ
∂θ
+
u
R
R
=
1
2µ
σ
θθ
,
e
xx
=
∂u
x
∂x
=
1
2µ
σ
xx
,
e
Rθ
=
R
2
∂
∂R
u
θ
R
+
1
2R
∂u
R
∂θ
=
1
2µ
σ
Rθ
,
e
θx
=
1
2R
∂u
x
∂θ
+
1
2
∂u
θ
∂x
=
1
2µ
σ
θx
,
e
xR
=
1
2
∂u
R
∂x
+
1
2
∂u
x
∂R
=
1
2µ
σ
xR
.
Vorticity (ω = ∇ × u)
ω
R
=
1
R
∂u
x
∂θ
−
∂u
θ
∂x
,
ω
θ
=
∂u
R
∂x
−
∂u
x
∂R
,
ω
x
=
1
R
∂
∂R
(Ru
θ
) −
1
R
∂u
R
∂θ
.
Equation of continuity
∂ρ
∂t
+
1
R
∂
∂R
(ρRu
R
) +
1
R
∂
∂θ
(ρu
θ
) +
∂
∂x
(ρu
x
) = 0 .
Navier–Stokes equations with constant ρ and ν, and no body force
∂u
R
∂t
+ (u · ∇)u
R
−
u
2
θ
R
=−
1
ρ
∂p
∂R
+ ν
∇
2
u
R
−
u
R
R
2
−
2
R
2
∂u
θ
∂θ
,
∂u
θ
∂t
+ (u · ∇)u
θ
+
u
R
u
θ
R
=−
1
ρR
∂p
∂θ
+ ν
∇
2
u
θ
+
2
R
2
∂u
R
∂θ
−
u
θ
R
2
,
∂u
x
∂t
+ (u · ∇)u
x
=−
1
ρ
∂p
∂x
+ ν∇
2
u
x
,
where
u · ∇ = u
R
∂
∂R
+
u
θ
R
∂
∂θ
+ u
x
∂
∂x
,
∇
2
=
1
R
∂
∂R
R
∂
∂R
+
1
R
2
∂
2
∂θ
2
+
∂
2
∂x
2
.
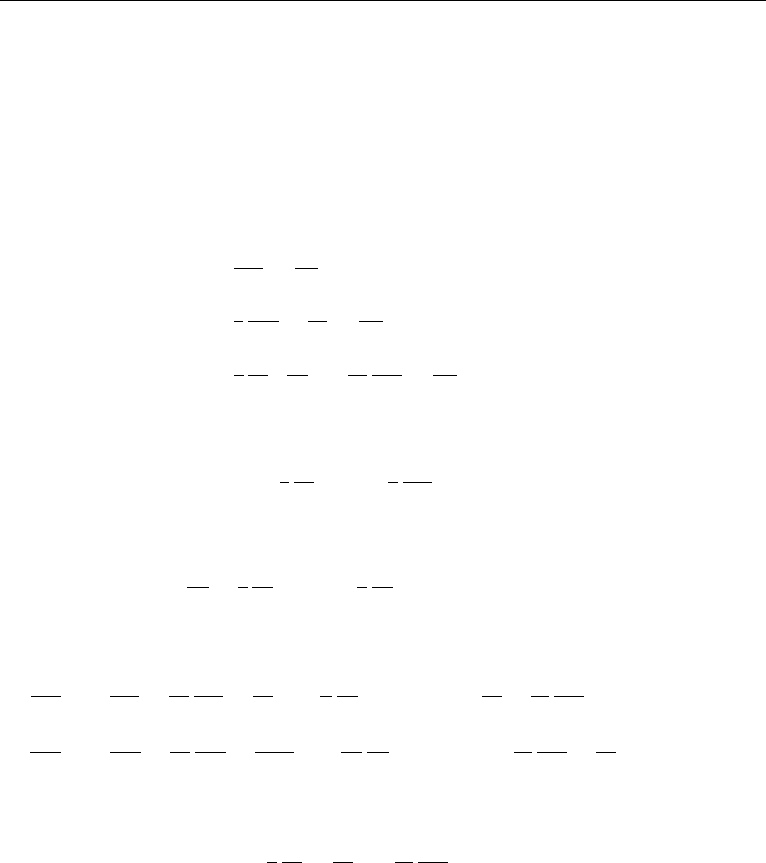
B3. Spherical Polar Coordinates 847
B2. Plane Polar Coordinates
The plane polar coordinates are (r, θ ), where r is the distance from the origin
(Figure 3.1a). The equations for plane polar coordinates can be obtained from
those of the cylindrical coordinates presented in Section B1, replacing R by r and
suppressing all components and derivatives in the axial direction x. Some of the
expressions are repeated here because of their frequent occurrence.
Strain rate and viscous stress (for incompressible form σ
ij
= 2µe
ij
)
e
rr
=
∂u
r
∂r
=
1
2µ
σ
rr
,
e
θθ
=
1
r
∂u
θ
∂θ
+
u
r
r
=
1
2µ
σ
θθ
,
e
rθ
=
r
2
∂
∂r
u
θ
r
+
1
2r
∂u
r
∂θ
=
1
2µ
σ
rθ
.
Vorticity
ω
z
=
1
r
∂
∂r
(ru
θ
) −
1
r
∂u
r
∂θ
.
Equation of continuity
∂ρ
∂t
+
1
r
∂
∂r
(ρru
r
) +
1
r
∂
∂θ
(ρu
θ
) = 0 .
Navier–Stokes equations with constant ρ and ν, and no body force
∂u
r
∂t
+ u
r
∂u
r
∂r
+
u
θ
r
∂u
r
∂θ
−
u
2
θ
r
=−
1
ρ
∂p
∂r
+ ν
∇
2
u
r
−
u
r
r
2
−
2
r
2
∂u
θ
∂θ
,
∂u
θ
∂t
+ u
r
∂u
θ
∂r
+
u
θ
r
∂u
θ
∂θ
+
u
r
u
θ
r
=−
1
ρr
∂p
∂θ
+ ν
∇
2
u
θ
+
2
r
2
∂u
r
∂θ
−
u
θ
r
2
,
where
∇
2
=
1
r
∂
∂r
r
∂
∂r
+
1
r
2
∂
2
∂θ
2
.
B3. Spherical Polar Coordinates
The spherical polar coordinates used are (r,θ,ϕ), where ϕ is the azimuthal angle
(Figure 3.1c). Equations are presented assuming ψ is a scalar, and
u = i
r
u
r
+ i
θ
u
θ
+ i
ϕ
u
ϕ
,
where i
r
, i
θ
, and i
ϕ
are the local unit vectors at a point.

848 Appendix B: Curvilinear Coordinates
Gradient of a scalar
∇ψ = i
r
∂ψ
∂r
+ i
θ
1
r
∂ψ
∂θ
+ i
ϕ
1
r sin θ
∂ψ
∂ϕ
.
Laplacian of a scalar
∇
2
ψ =
1
r
2
∂
∂r
r
2
∂ψ
∂r
+
1
r
2
sin θ
∂
∂θ
sin θ
∂ψ
∂θ
+
1
r
2
sin
2
θ
∂
2
ψ
∂ϕ
2
.
Divergence of a vector
∇ · u =
1
r
2
∂(r
2
u
r
)
∂r
+
1
r sin θ
∂(u
θ
sin θ)
∂θ
+
1
r sin θ
∂u
θ
∂ϕ
.
Curl of a vector
∇ × u =
i
r
r sin θ
∂(u
ϕ
sin θ)
∂θ
−
∂u
θ
∂ϕ
+
i
θ
r
1
sin θ
∂u
r
∂ϕ
−
∂(ru
ϕ
)
∂r
+
i
ϕ
r
∂(ru
θ
)
∂r
−
∂u
r
∂θ
.
Laplacian of a vector
∇
2
u = i
r
∇
2
u
r
−
2u
r
r
2
−
2
r
2
sin θ
∂(u
θ
sin θ)
∂θ
−
2
r
2
sin θ
∂u
ϕ
∂ϕ
+ i
θ
∇
2
u
θ
+
2
r
2
∂u
r
∂θ
−
u
θ
r
2
sin
2
θ
−
2 cos θ
r
2
sin
2
θ
∂u
ϕ
∂ϕ
+ i
ϕ
∇
2
u
ϕ
+
2
r
2
sin θ
∂u
r
∂ϕ
+
2 cos θ
r
2
sin
2
θ
∂u
θ
∂ϕ
−
u
ϕ
r
2
sin
2
θ
.
Strain rate and viscous stress (for incompressible form σ
ij
= 2µe
ij
)
e
rr
=
∂u
r
∂r
=
1
2µ
σ
rr
,
e
θθ
=
1
r
∂u
θ
∂θ
+
u
r
r
=
1
2µ
σ
θθ
,
e
ϕϕ
=
1
r sin θ
∂u
ϕ
∂ϕ
+
u
r
r
+
u
θ
cot θ
r
=
1
2µ
σ
ϕϕ
,
e
θϕ
=
sin θ
2r
∂
∂θ
u
ϕ
sin θ
+
1
2r sin θ
∂u
θ
∂ϕ
=
1
2µ
σ
θϕ
,
e
ϕr
=
1
2r sin θ
∂u
r
∂ϕ
+
r
2
∂
∂r
u
ϕ
r
=
1
2µ
σ
ϕr
,
e
rθ
=
r
2
∂
∂r
u
θ
r
+
1
2r
∂u
r
∂θ
=
1
2µ
σ
rθ
.
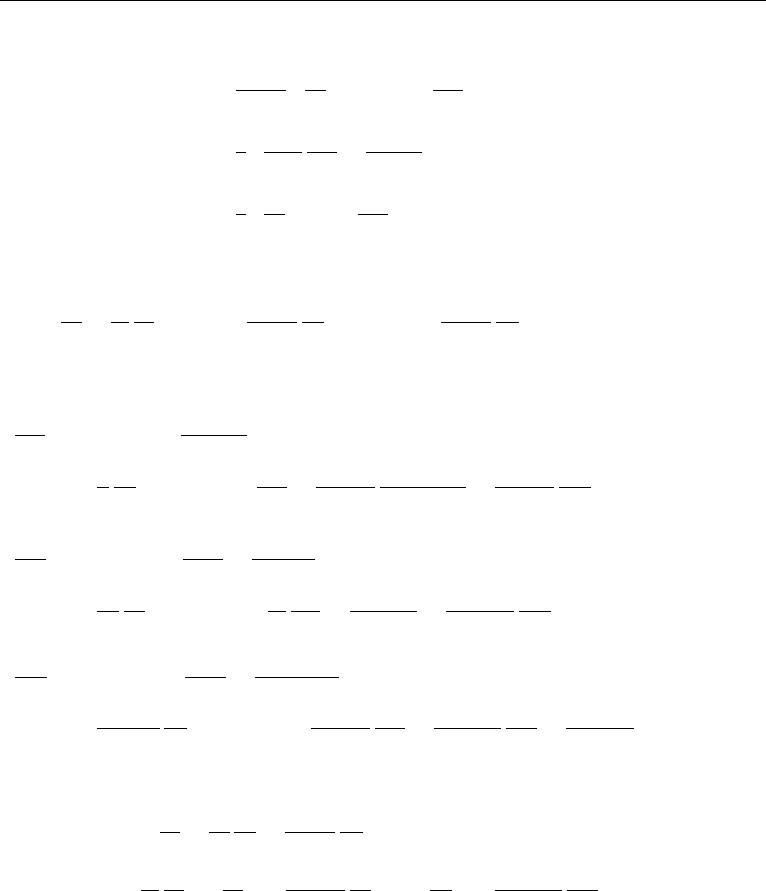
B3. Spherical Polar Coordinates 849
Vorticity
ω
r
=
1
r sin θ
∂
∂θ
(u
ϕ
sin θ)−
∂u
θ
∂ϕ
,
ω
θ
=
1
r
1
sin θ
∂u
r
∂ϕ
−
∂(ru
ϕ
)
∂r
,
ω
ϕ
=
1
r
∂
∂r
(ru
θ
) −
∂u
r
∂θ
.
Equation of continuity
∂ρ
∂t
+
1
r
2
∂
∂r
(ρr
2
u
r
) +
1
r sin θ
∂
∂θ
(ρu
θ
sin θ)+
1
r sin θ
∂
∂ϕ
(ρu
ϕ
) = 0 .
Navier–Stokes equations with constant ρ and ν, and no body force
∂u
r
∂t
+ (u · ∇)u
r
−
u
2
θ
+ u
2
ϕ
r
=−
1
ρ
∂p
∂r
+ ν
∇
2
u
r
−
2u
r
r
2
−
2
r
2
sin θ
∂(u
θ
sin θ)
∂θ
−
2
r
2
sin θ
∂u
ϕ
∂ϕ
,
∂u
θ
∂t
+ (u · ∇)u
θ
+
u
r
u
θ
r
−
u
2
ϕ
cot θ
r
=−
1
ρr
∂p
∂θ
+ ν
∇
2
u
θ
+
2
r
2
∂u
r
∂θ
−
u
θ
r
2
sin
2
θ
−
2 cos θ
r
2
sin
2
θ
∂u
ϕ
∂ϕ
,
∂u
ϕ
∂t
+ (u · ∇)u
ϕ
+
u
ϕ
u
r
r
+
u
θ
u
ϕ
cot θ
r
=−
1
ρr sin θ
∂p
∂ϕ
+ ν
∇
2
u
ϕ
+
2
r
2
sin θ
∂u
r
∂ϕ
+
2 cos θ
r
2
sin
2
θ
∂u
θ
∂ϕ
−
u
ϕ
r
2
sin
2
θ
,
where
u · ∇ = u
r
∂
∂r
+
u
θ
r
∂
∂θ
+
u
ϕ
r sin θ
∂
∂ϕ
,
∇
2
=
1
r
2
∂
∂r
r
2
∂
∂r
+
1
r
2
sin θ
∂
∂θ
sin θ
∂
∂θ
+
1
r
2
sin
2
θ
∂
2
∂ϕ
2
.
This page intentionally left blank

Appendix C
Founders of
Modern Fluid Dynamics
Ludwig Prandtl (1875–1953) ......... 851
Geoffrey Ingram Taylor (1886–1975) . . 852
Supplemental Reading ............ 853
Ludwig Prandtl (1875−1953)
Ludwig Prandtl was born in Freising, Germany, in 1875. He studied mechanical
engineering in Munich. For his doctoral thesis he worked on a problem on elasticity
under August F
¨
oppl, who himself did pioneering work in bringing together applied
and theoretical mechanics. Later, Prandtl became F
¨
oppl’s son-in-law, following the
good German academic tradition in those days. In 1901, he became professor of
mechanics at the University of Hanover, where he continued his earlier efforts to
provide a sound theoretical basis for fluid mechanics. The famous mathematician
Felix Klein, who stressed the use of mathematics in engineering education, became
interested in Prandtl and enticed him to come to the University of G
¨
ottingen. Prandtl
was a great admirer of Klein and kept a large portrait of him in his office. He served as
professor of applied mechanics at G
¨
ottingen from 1904 to 1953; the quiet university
town of G
¨
ottingen became an international center of aerodynamic research.
In 1904, Prandtl conceived the idea of a boundary layer, which adjoins the surface
of a body moving through a fluid, and is perhaps the greatest single discovery in the
history of fluid mechanics. He showed that frictional effects in a slightly viscous fluid
are confined to a thin layer near the surface of the body; the rest of the flow can
be considered inviscid. The idea led to a rational way of simplifying the equations
of motion in the different regions of the flow field. Since then the boundary layer
technique has been generalized and has become a most useful tool in many branches
of science.
His work on wings of finite span (the Prandtl–Lanchester wing theory) eluci-
dated the generation of induced drag. In compressible fluid motions he contributed the
Prandtl–Glauert rule of subsonic flow, the Prandtl–Meyer expansion fan in supersonic
flow around a corner, and published the first estimate of the thickness of a shock wave.
851
©2010 Elsevier Inc. All rights reserved.
DOI: 10.1016/B978-0-12-381399-2.50020-4
