Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

752 Compressible Flow

The Mach cone becomes wider as M decreases and becomes a plane front (that is,

µ = 90

◦

) when M = 1.

The point source considered here could be part of a solid body, which sends out

pressure waves as it moves through the ﬂuid. Moreover, Figure 16.18c applies equally

if the point source is stationary and the ﬂuid is approaching at a supersonic speed U .

It is clear that in a supersonic ﬂow an observer outside the Mach cone would not

“hear” a signal emitted by a point disturbance, hence this region is called the zone

of silence. In contrast, the region inside the Mach cone is called the zone of action,

within which the effects of the disturbance are felt. This explains why the sound of a

supersonic airplane does not reach an observer until the Mach cone arrives, after the

plane has passed overhead.

At every point in a planar supersonic ﬂow there are two Mach lines, oriented at

±µ to the local direction of ﬂow. Information propagates along these lines, which

are the characteristics of the governing differential equation. It can be shown that the

nature of the governing differential equation is hyperbolic in a supersonic ﬂow and

elliptic in a subsonic ﬂow.

10. Oblique Shock Wave

In Section 6 we examined the case of a normal shock wave, oriented perpendicular to

the direction of ﬂow, in which the velocity changes from supersonic to subsonic values.

However, a shock wave can also be oriented obliquely to the ﬂow (Figure 16.19a),

the velocity changing from V

to V

. The ﬂow can be analyzed by considering a

normal shock across which the normal velocity varies from u

to u

and superposing

a velocity v parallel to it (Figure 16.19b). By considering conservation of momentum

in a direction tangential to the shock, we may show that v is unchanged across a shock

(Exercise 12). The magnitude and direction of the velocities on the two sides of the

shock are



+ v

oriented at σ = tan

−1

/v),



+ v

oriented at σ − δ = tan

−1

/v).

Figure 16.19 (a) Oblique shock wave in which δ = deﬂection angle and σ = shock angle; and

(b) analysis by considering a normal shock and superposing a velocity v parallel to the shock.

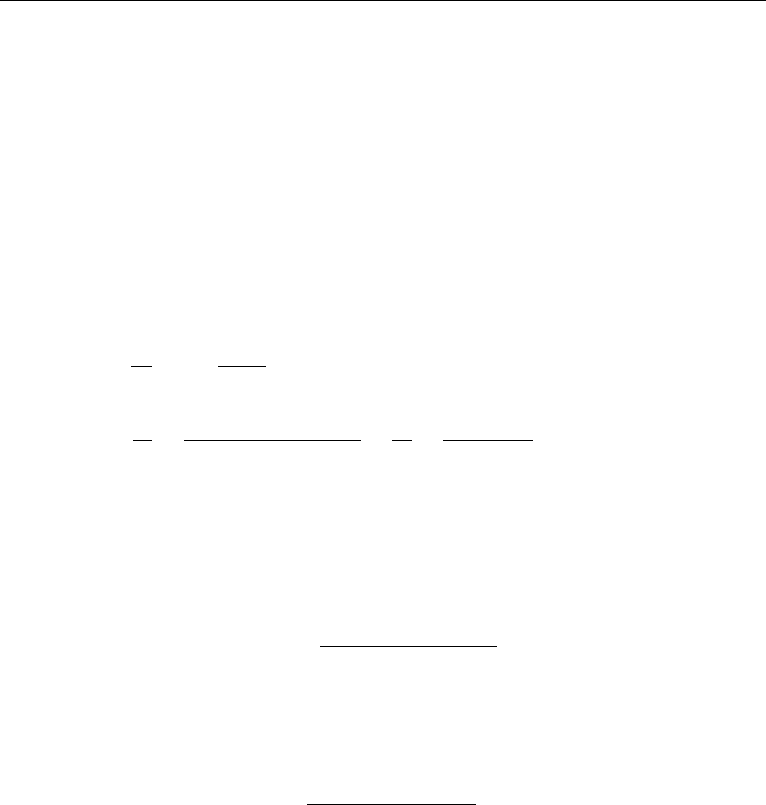
10. Oblique Shock Wave 753

The normal Mach numbers are

= u

= M

sin σ>1,

= u

= M

sin(σ − δ) < 1.

Because u

, there is a sudden change of direction of ﬂow across the shock; in

fact the ﬂow turns toward the shock by an amount δ. The angle σ is called the shock

angle or wave angle and δ is called the deﬂection angle.

Superposition of the tangential velocity v does not affect the static properties,

which are therefore the same as those for a normal shock. The expressions for the ratios

, ρ

/ρ

, T

, and (S

−S

)/C

are therefore those given by equations (16.31),

(16.33)–(16.35), if M

is replaced by the normal component of the upstream Mach

number M

sin σ . For example,

= 1 +

2γ

γ + 1

sin

σ − 1), (16.39)

(γ + 1)M

sin

(γ − 1)M

sin

σ + 2

tan σ

tan (σ − δ)

. (16.40)

The normal shock table, Table 16.2, is therefore also applicable to oblique shock

wavesifweuseM

sin σ in place of M

The relation between the upstream and downstream Mach numbers can be found

from equation (16.32) by replacing M

by M

sin σ and M

by M

sin (σ − δ). This

gives

sin

(σ − δ) =

(γ − 1)M

sin

σ + 2

2γM

sin

σ + 1 −γ

. (16.41)

An important relation is that between the deﬂection angle δ and the shock angle σ

for a given M

, given in equation (16.40). Using the trigonometric identity for tan (σ −

δ), this becomes

tan δ = 2 cot σ

sin

σ − 1

(γ + cos 2σ)+ 2

. (16.42)

A plot of this relation is given in Figure 16.20. The curves represent δ vs σ for constant

. The value of M

varies along the curves, and the locus of points corresponding

to M

= 1 is indicated. It is apparent that there is a maximum deﬂection angle δ

max

for oblique shock solutions to be possible; for example, δ

max

= 23

◦

for M

= 2.

ForagivenM

, δ becomes zero at σ = π/2 corresponding to a normal shock, and

at σ = µ = sin

−1

(1/M

) corresponding to the Mach angle. For a ﬁxed M

and

δ<δ

max

, there are two possible solutions: a weak shock corresponding to a smaller

σ , and a strong shock corresponding to a larger σ . It is clear that the ﬂow downstream

of a strong shock is always subsonic; in contrast, the ﬂow downstream of a weak

shock is generally supersonic, except in a small range in which δ is slightly smaller

than δ

max

754 Compressible Flow

Figure 16.20 Plot of oblique shock solution. The strong shock branch is indicated by dashed lines, and

the heavy dotted line indicates the maximum deﬂection angle δ

max

. (From NACA Report 1135.)

Generation of Oblique Shock Waves

Consider the supersonic ﬂow past a wedge of half-angle δ, or the ﬂow over a wall

that turns inward by an angle δ (Figure 16.21). If M

and δ are given, then σ can be

obtained from Figure 16.20, and M

(and therefore M

= M

/sin(σ − δ)) can be

obtained from the shock table, Table 16.2. An attached shock wave, corresponding

to the weak solution, forms at the nose of the wedge, such that the ﬂow is parallel

to the wedge after turning through an angle δ. The shock angle σ decreases to the

Mach angle µ

= sin

−1

(1/M

) as the deﬂection δ tends to zero. It is interesting that

the corner velocity in a supersonic ﬂow is ﬁnite. In contrast, the corner velocity in

a subsonic (or incompressible) ﬂow is either zero or inﬁnite, depending on whether

the wall shape is concave or convex. Moreover, the streamlines in Figure 16.21 are

straight, and computation of the ﬁeld is easy. By contrast, the streamlines in a subsonic

ﬂow are curved, and the computation of the ﬂow ﬁeld is not easy. The basic reason

for this is that, in a supersonic ﬂow, the disturbances do not propagate upstream of

Mach lines or shock waves emanating from the disturbances, hence the ﬂow ﬁeld can

be constructed step by step, proceeding downstream. In contrast, the disturbances

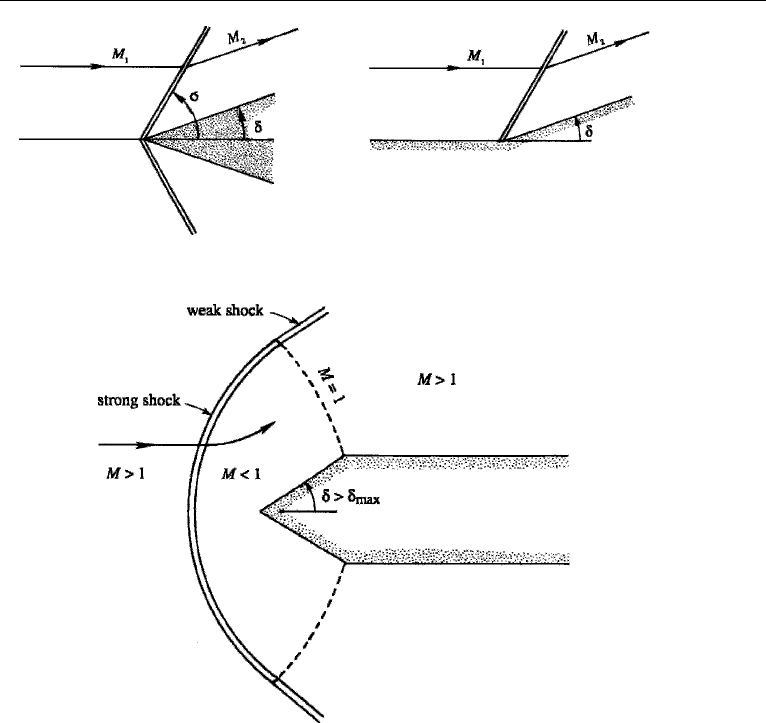
10. Oblique Shock Wave 755

Figure 16.21 Oblique shocks in supersonic ﬂow.

Figure 16.22 Detached shock.

propagate both upstream and downstream in a subsonic ﬂow, so that all features in

the entire ﬂow ﬁeld are related to each other.

As δ is increased beyond δ

max

, attached oblique shocks are not possible, and

a detached curved shock stands in front of the body (Figure 16.22). The central

streamline goes through a normal shock and generates a subsonic ﬂow in front of the

wedge. The strong shock solution of Figure 16.20 therefore holds near the nose of the

body. Farther out, the shock angle decreases, and the weak shock solution applies.

If the wedge angle is not too large, then the curved detached shock in Figure 16.22

becomes an oblique attached shock as the Mach number is increased. In the case

of a blunt-nosed body, however, the shock at the leading edge is always detached,

although it moves closer to the body as the Mach number is increased.

We see that shock waves may exist in supersonic ﬂows and their location and

orientation adjust to satisfy boundary conditions. In external ﬂows, such as those just

756 Compressible Flow

described, the boundary condition is that streamlines at a solid surface must be tangent

to that surface. In duct ﬂows the boundary condition locating the shock is usually the

downstream pressure.

The Weak Shock Limit

A simple and useful expression can be derived for the pressure change across a weak

shock by considering the limiting case of a small deﬂection angle δ. We ﬁrst need to

simplify equation (16.42) by noting that as δ → 0, the shock angle σ tends to the

Mach angle µ

= sin

−1

(1/M

Also from equation (16.39) we note that (p

−p

)/p

→ 0asM

sin

σ −1 → 0,

(as σ → µ and δ → 0). Then from equations (16.39) and (16.42)

tan δ = 2 cot σ

γ + 1

2γ



− p



(γ + 1 − 2 sin

σ)+ 2

. (16.43)

As δ → 0, tan δ ≈ δ, cot µ =



− 1, sin σ ≈ 1/M

, and

− p



γM



− 1

δ.

(16.44)

The interesting point is that relation (16.44) is also applicable to a weak expansion

wave and not just a weak compression wave. By this we mean that the pressure

increase due to a small deﬂection of the wall toward the ﬂow is the same as the

pressure decrease due to a small deﬂection of the wall away from the ﬂow. This is

because the entropy change across a shock goes to zero much faster than the rate at

which the pressure difference across the wave decreases as our study of normal shock

waves has shown. Very weak “shock waves” are therefore approximately isentropic

or reversible. Relationships for a weak shock wave can therefore be applied to a weak

expansion wave, except for some sign changes. In Section 12, equation (16.44) will

be applied in estimating the lift and drag of a thin airfoil in supersonic ﬂow.

11. Expansion and Compression in Supersonic Flow

Consider the supersonic ﬂow over a gradually curved wall (Figure 16.23). The

wavefronts are now Mach lines, inclined at an angle of µ = sin

−1

(1/M) to the local

direction of ﬂow. The ﬂow orientation and Mach number are constant on each Mach

line. In the case of compression, the Mach number decreases along the ﬂow, so that

the Mach angle increases. The Mach lines therefore coalesce and form an oblique

shock. In the case of gradual expansion, the Mach number increases along the ﬂow

and the Mach lines diverge.

If the wall has a sharp deﬂection away from the approaching stream, then the

pattern of Figure 16.23b takes the form of Figure 16.24. The ﬂow expands through

a “fan” of Mach lines centered at the corner, called the Prandtl–Meyer expansion

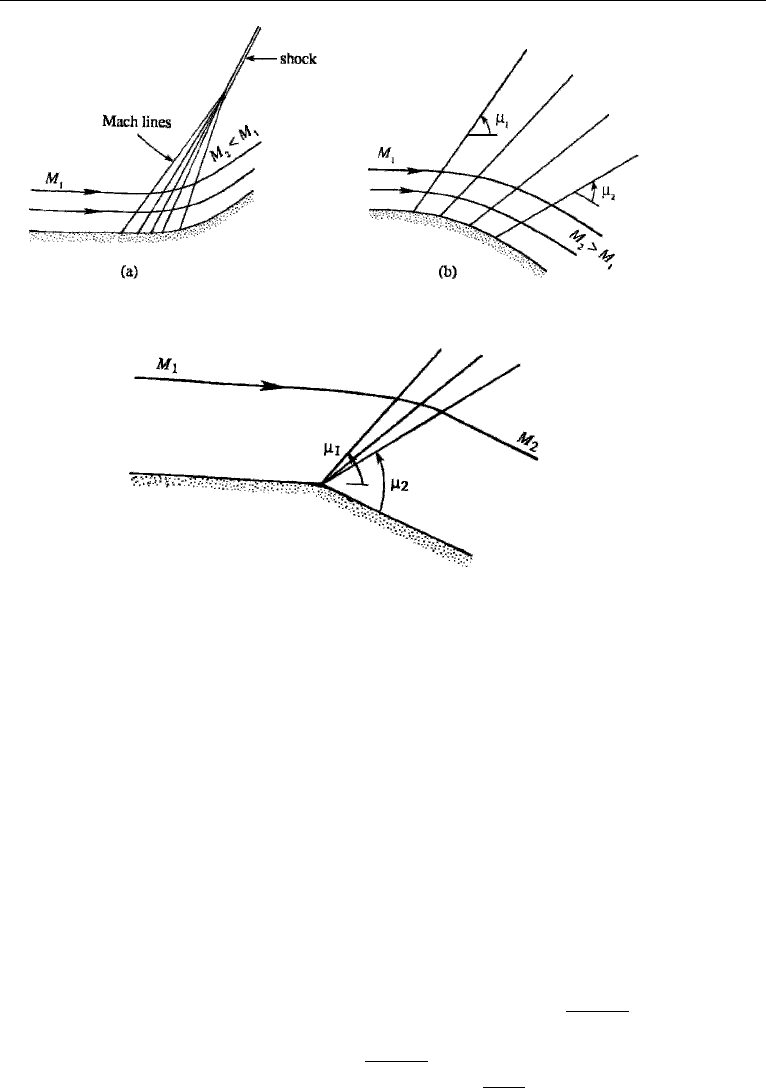
11. Expansion and Compression in Supersonic Flow 757

Figure 16.23 Gradual compression and expansion in supersonic ﬂow: (a) gradual compression, resulting

in shock formation; and (b) gradual expansion.

Figure 16.24 The Prandtl–Meyer expansion fan.

fan. The Mach number increases through the fan, with M

. The ﬁrst Mach line

is inclined at an angle of µ

to the local ﬂow direction, while the last Mach line is

inclined at an angle of µ

to the local ﬂow direction. The pressure falls gradually along

a streamline through the fan. (Along the wall, however, the pressure remains constant

along the upstream wall, falls discontinuously at the corner, and then remains constant

along the downstream wall.) Figure 16.24 should be compared with Figure 16.21, in

which the wall turns inward and generates a shock wave. By contrast, the expansion

in Figure 16.24 is gradual and isentropic.

The ﬂow through a Prandtl–Meyer fan is calculated as follows. From

Figure 16.19b, conservation of momentum tangential to the shock shows that the

tangential velocity is unchanged, or

cos σ = V

cos(σ − δ) = V

(cos σ cos δ + sin σ sin δ).

We are concerned here with very small deﬂections, δ → 0soσ → µ. Here, cos δ ≈ 1,

sin δ ≈ δ, V

≈ V

(1 + δ tan σ), so (V

− V

)/V

≈ δ tan σ ≈−δ/

√

− 1.

Regarding this as appropriate for inﬁnitesimal change in V for an inﬁnitesimal

deﬂection, we can write this as dδ =−dV

√

− 1/V (ﬁrst quadrant deﬂection).

Because V = Mc, dV/V = dM/M + dc/c. With c =

√

γRT for a perfect gas,

758 Compressible Flow

dc/c = dT/2T . Using equation (16.20) for adiabatic ﬂow of a perfect gas, dT/T

=−(γ − 1)M dM/[1 + ((γ − 1)/2)M

Then

dδ =−

√

− 1

1 + ((γ − 1)/2)M

Integrating δ from 0 (radians) and M from 1 gives

δ + ν(M) = const.,

where

ν(M) =



√

− 1

1 + ((γ − 1)/2)M



γ + 1

γ − 1

tan

−1



γ − 1

γ + 1

− 1) − tan

−1



− 1, (16.45)

is called the Prandtl–Meyer function. The sign of

√

− 1 originates

from the identiﬁcation of tan σ = tan µ = 1/

√

− 1 for a ﬁrst quadrant

deﬂection (upper half-plane). For a fourth quadrant deﬂection (lower half-plane),

tan µ =−1/

√

− 1. For example, in Figure 16.23 we would write

+ ν

) = δ

+ ν

where, for example, δ

,δ

, and M

are given. Then

) = δ

− δ

+ ν

In panel (a), δ

− δ

< 0, so ν

<ν

and M

. In panel (b), δ

− δ

> 0, so

>ν

and M

12. Thin Airfoil Theory in Supersonic Flow

Simple expressions can be derived for the lift and drag coefﬁcients of an airfoil in

supersonic ﬂow if the thickness and angle of attack are small. The disturbances caused

by a thin airfoil are small, and the total ﬂow can be built up by superposition of small

disturbances emanating from points on the body. Such a linearized theory of lift and

drag was developed by Ackeret. Because all ﬂow inclinations are small, we can use

the relation (16.44) to calculate the pressure changes due to a change in ﬂow direction.

We can write this relation as

p − p

∞

γM

∞



∞

− 1

, (16.46)

12. Thin Airfoil Theory in Supersonic Flow 759

where p

∞

and M

∞

refer to the properties of the free stream, and p is the pressure at

a point where the ﬂow is inclined at an angle δ to the free-stream direction. The sign

of δ determines the sign of (p − p

∞

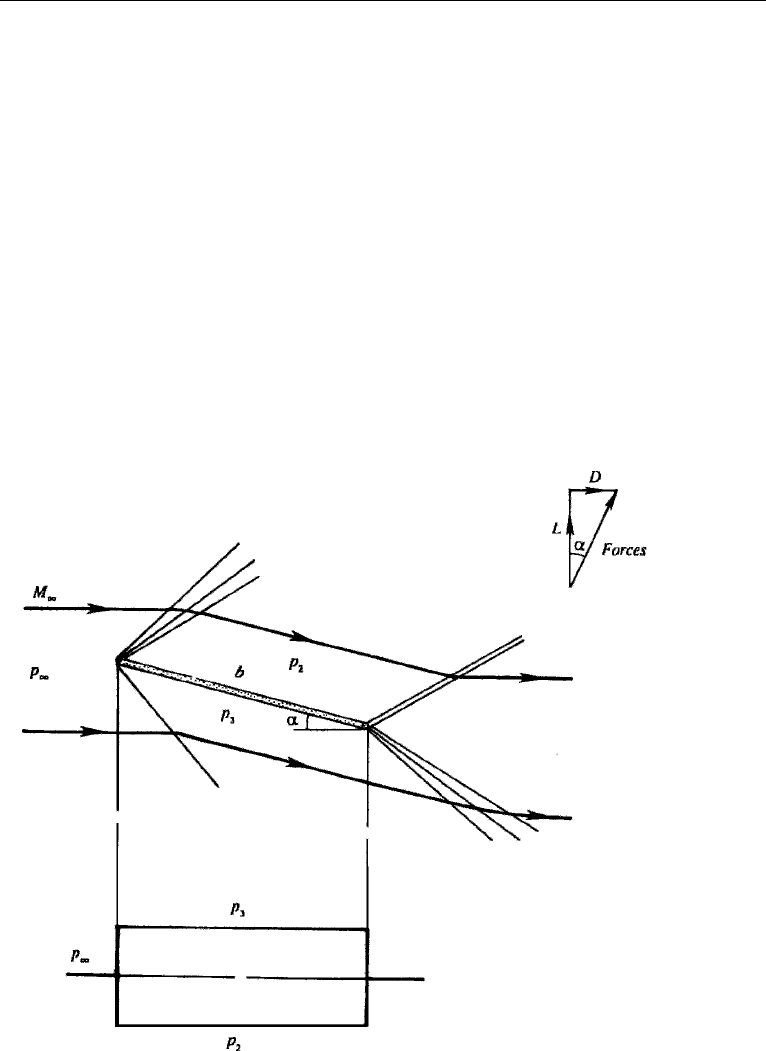
To see how the lift and drag of a thin body in a supersonic stream can be estimated,

consider a ﬂat plate inclined at a small angle α to a stream (Figure 16.25). At the

leading edge there is a weak expansion fan on the top surface and a weak oblique

shock on the bottom surface. The streamlines ahead of these waves are straight. The

streamlines above the plate turn through an angle α by expanding through a centered

fan, downstream of which they become parallel to the plate with a pressure p

∞

The upper streamlines then turn sharply across a shock emanating from the trailing

edge, becoming parallel to the free stream once again. Opposite features occur for

the streamlines below the plate. The ﬂow ﬁrst undergoes compression across a shock

coming from the leading edge, which results in a pressure p

∞

. It is, however,

not important to distinguish between shocks and expansion waves in Figure 16.25,

because the linearized theory treats them the same way, except for the sign of the

pressure changes they produce.

Figure 16.25 Inclined ﬂat plate in a supersonic stream. The upper panel shows the ﬂow pattern and the

lower panel shows the pressure distribution.

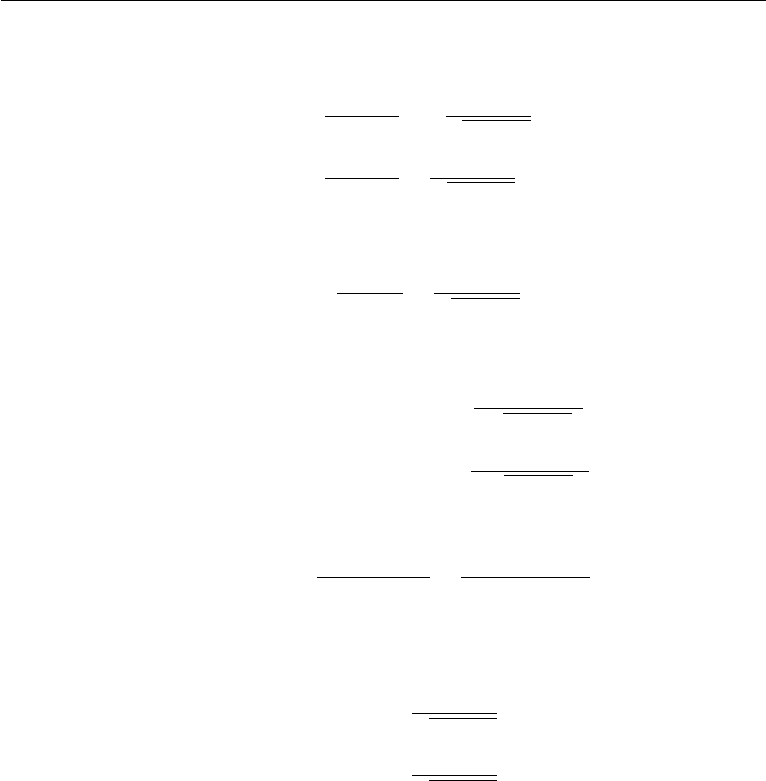
760 Compressible Flow

The pressures above and below the plate can be found from equation (16.46),

giving

− p

∞

=−

γM

∞



∞

− 1

− p

∞

γM

∞



∞

− 1

The pressure difference across the plate is therefore

− p

∞

2αγ M

∞



∞

− 1

If b is the chord length, then the lift and drag forces per unit span are

L = (p

− p

)b cos α 

2αγ M

∞



∞

− 1

D = (p

− p

)b sin α 

2α

γM

∞



∞

− 1

(16.47)

The lift coefﬁcient is deﬁned as

≡

(1/2)ρ

∞

(1/2)γp

∞

where we have used the relation ρU

= γpM

. Using equation (16.47), the lift and

drag coefﬁcients for a ﬂat lifting surface are



4α



∞

− 1



4α



∞

− 1

(16.48)

These expressions do not hold at transonic speeds M

∞

→ 1, when the process of

linearization used here breaks down. The expression for the lift coefﬁcient should be

compared to the incompressible expression C

 2πα derived in the preceding chap-

ter. Note that the ﬂow in Figure 16.25 does have a circulation because the velocities

at the upper and lower surfaces are parallel but have different magnitudes. However,

in a supersonic ﬂow it is not necessary to invoke the Kutta condition (discussed in

the preceding chapter) to determine the magnitude of the circulation. The ﬂow in

Figure 16.25 does leave the trailing edge smoothly.

The drag in equation (16.48) is the wave drag experienced by a body in a super-

sonic stream, and exists even in an inviscid ﬂow. The d’Alembert paradox therefore

does not apply in a supersonic ﬂow. The supersonic wave drag is analogous to the

gravity wave drag experienced by a ship moving at a speed greater than the velocity

Exercises 761

of surface gravity waves, in which a system of bow waves is carried with the ship.

The magnitude of the supersonic wave drag is independent of the value of the viscos-

ity, although the energy spent in overcoming this drag is ﬁnally dissipated through

viscous effects within the shock waves. In addition to the wave drag, additional drags

due to viscous and ﬁnite-span effects, considered in the preceding chapter, act on a

real wing.

In this connection, it is worth noting the difference between the airfoil shapes

used in subsonic and supersonic airplanes. Low-speed airfoils have a streamlined

shape, with a rounded nose and a sharp trailing edge. These features are not helpful

in supersonic airfoils. The most effective way of reducing the drag of a supersonic

airfoil is to reduce its thickness. Supersonic wings are characteristically thin and have

a sharp leading edge.

Exercises

1. The critical area A

∗

of a duct ﬂow was deﬁned in Section 4. Show that

the relation between A

∗

and the actual area A at a section, where the Mach number

equals M, is that given by equation (16.23). This relation was not proved in the text.

[Hint: Write

∗

ρu

∗



∗

Then use the relations given in Section 4.]

2. The entropy change across a normal shock is given by equation (16.35). Show

that this reduces to expression (16.36) for weak shocks. [Hint: Let M

− 1  1.

Write the terms within the two brackets [][]in equation (16.35) in the form

[1 + ε

][1 + ε

]

, where ε

and ε

are small quantities. Then use series expansion

ln (1 + ε) = ε − ε

/2 +ε

/3 +···. This gives equation (16.36) times a function of

in which we can set M

= 1.]

3. Show that the maximum velocity generated from a reservoir in which the

stagnation temperature equals T

max



What are the corresponding values of T and M?

4. In an adiabatic ﬂow of air through a duct, the conditions at two points are

= 250 m/s,

= 300 K,

= 200 kPa,

= 300 m/s,

= 150 kPa.