Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

732 Compressible Flow

Figure 16.7 Convergent–divergent passages in which the condition at the throat is not sonic.

that the nozzle must converge in the subsonic portion and diverge in the supersonic

portion. Such a nozzle is called a convergent–divergent nozzle. From Figure 16.6 it

is clear that the Mach number must be unity at the throat, where the area is neither

increasing nor decreasing. This is consistent with equation (16.27), which shows that

du can be nonzero at the throat only if M = 1. It follows that the sonic velocity can

be achieved only at the throat of a nozzle or a diffuser and nowhere else.

It does not, however, follow that M must necessarily be unity at the throat.

According to equation (16.27), we may have a case where M = 1 at the throat if

du = 0 there. As an example, note that the ﬂow in a convergent–divergent tube may

be subsonic everywhere, with M increasing in the convergent portion and decreas-

ing in the divergent portion, with M = 1 at the throat (Figure 16.7a). The ﬁrst half

of the tube here is acting as a nozzle, whereas the second half is acting as a dif-

fuser. Alternatively, we may have a convergent–divergent tube in which the ﬂow is

supersonic everywhere, with M decreasing in the convergent portion and increasing

in the divergent portion, and again M = 1 at the throat (Figure 16.7b).

Example 16.1

The nozzle of a rocket motor is designed to generate a thrust of 30,000 N when

operating at an altitude of 20 km. The pressure inside the combustion chamber is

1000 kPa while the temperature is 2500 K. The gas constant of the ﬂuid in the jet is

R = 280 m

/(s

K), and γ = 1.4. Assuming that the ﬂow in the nozzle is isentropic,

calculate the throat and exit areas. Use the isentropic table (Table 16.1).

Solution: At an altitude of 20 km, the pressure of the standard atmosphere

(SectionA4 in Appendix A) is 5467 Pa. If subscripts “0” and “e” refer to the stagnation

and exit conditions, then a summary of the information given is as follows:

= 5467 Pa,

= 1000 kPa,

6. Normal Shock Wave 733

= 2500 K,

Thrust = ρ

= 30,000 N.

Here, we have used the facts that the thrust equals mass ﬂow rate times the exit velocity,

and the pressure inside the combustion chamber is nearly equal to the stagnation

pressure. The pressure ratio at the exit is

5467

(1000)(1000)

= 5.467 ×10

−3

For this ratio of p

, the isentropic table (Table 16.1) gives

= 4.15,

∗

= 12.2,

= 0.225.

The exit temperature and density are therefore

= (0.225)(2500) = 562 K,

= p

/RT

= 5467/(280)(562) = 0.0347 kg/ m

The exit velocity is

= M



γRT

= 4.15



(1.4)(280)(562) = 1948 m/s.

The exit area is found from the expression for thrust:

Thrust

30,000

(0.0347)(1948)

= 0.228 m

Because A

∗

= 12.2, the throat area is

∗

0.228

12.2

= 0.0187 m

6. Normal Shock Wave

A shock wave is similar to a sound wave except that it has ﬁnite strength. The thickness

of such a wavefront is of the order of micrometers, so that the properties vary almost

discontinuously across a shock wave. The high gradients of velocity and temperature

result in entropy production within the wave, due to which the isentropic relations

734 Compressible Flow

cannot be used across the shock. In this section we shall derive the relations between

properties of the ﬂow on the two sides of a normal shock, where the wavefront is

perpendicular to the direction of ﬂow. We shall treat the shock wave as a discontinuity;

a treatment of Navier-Strokes shock structure is given at the end of this section.

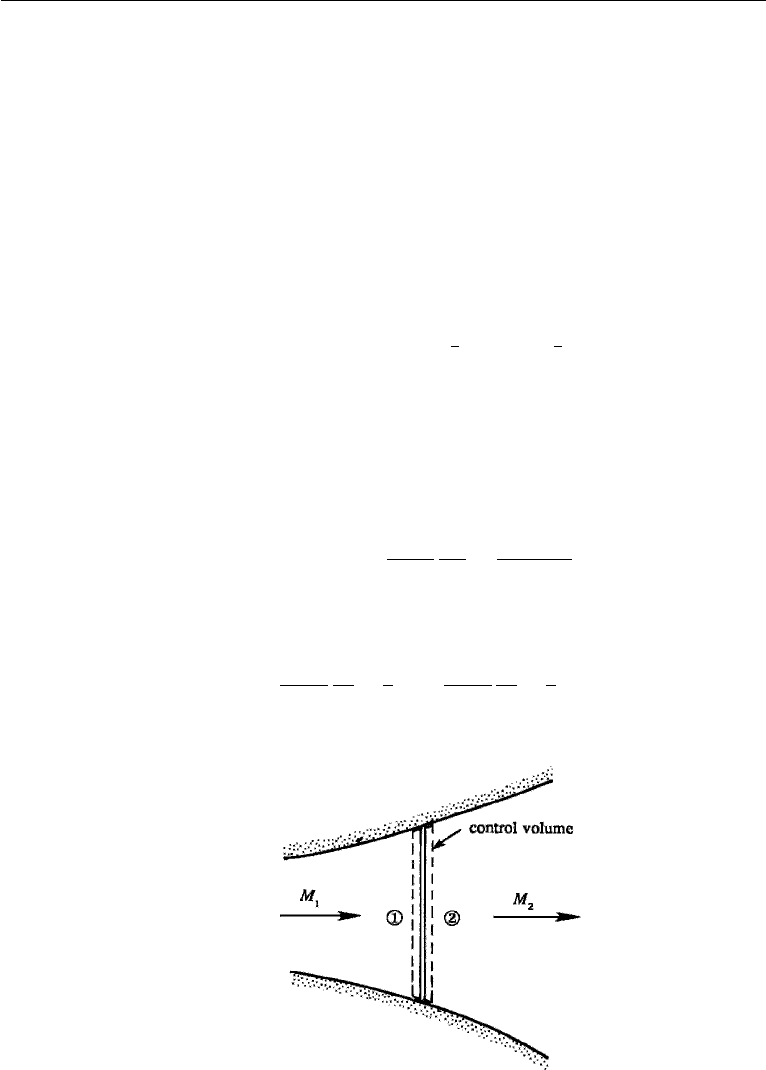
To derive the relationships between the properties on the two sides of the shock,

consider a control volume shown in Figure 16.8, where the sections 1 and 2 can

be taken arbitrarily close to each other because of the discontinuous nature of the

wave. The area change between the upstream and the downstream sides can then be

neglected. The basic equations are

Continuity: ρ

= ρ

, (16.28)

x-momentum: p

− p

= ρ

− ρ

, (16.29)

Energy: h

= h

In the application of the momentum theorem, we have neglected any frictional drag

from the walls because such forces go to zero as the wave thickness goes to zero.

Note that we cannot use the Bernoulli equation because the process inside the wave is

dissipative. We have written down four unknowns (h

, u

, p

, ρ

) and three equations.

The additional relation comes from the perfect gas relationship

h = C

T =

γR

γ − 1

ρR

γp

(γ − 1)ρ

so that the energy equation becomes

γ − 1

. (16.30)

Figure 16.8 Normal shock wave.

6. Normal Shock Wave 735

We now have three unknowns (u

, p

, ρ

) and three equations (16.28)–(16.30).

Elimination of ρ

and u

from these gives, after some algebra,

= 1 +

2γ

γ + 1



γp

− 1



This can be expressed in terms of the upstream Mach number M

by noting that

ρu

/γp = u

/γ RT = M

. The pressure ratio then becomes

= 1 +

2γ

γ + 1

− 1). (16.31)

Let us now derive a relation between M

and M

. Because ρu

= ρc

ρ(γp/ρ)M

= γpM

, the momentum equation (16.29) gives

+ γp

= p

+ γp

Using equation (16.31), this gives

(γ − 1)M

+ 2

2γM

+ 1 − γ

(16.32)

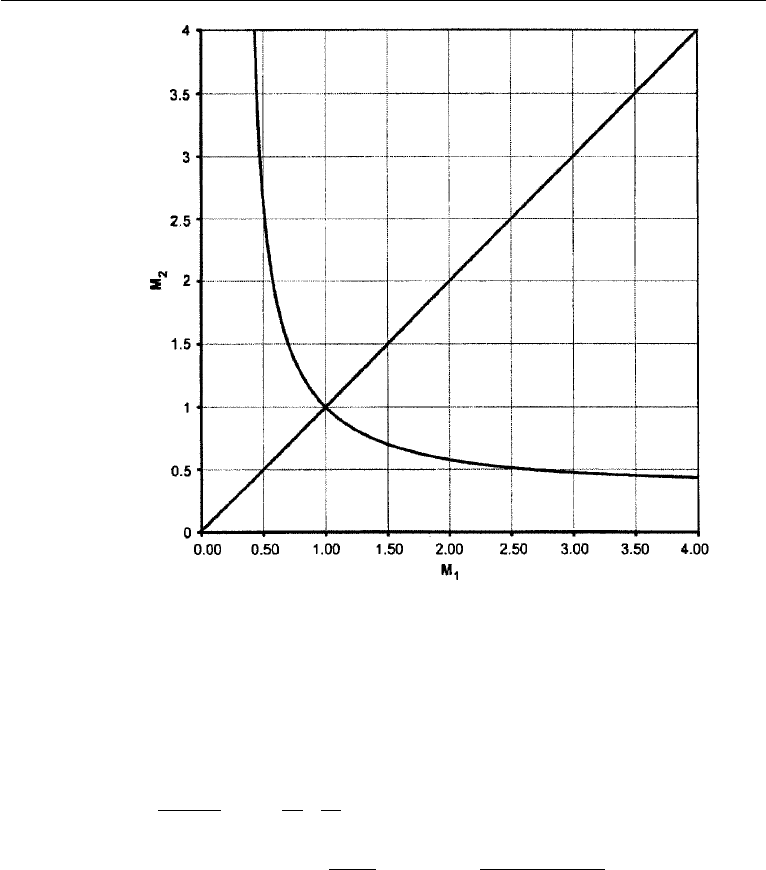
which is plotted in Figure 16.9. Because M

= M

(state 2 = state 1) is a solution

of equations (16.28)–(16.30), that is shown as well indicating two possible solutions

for M

for all M

> [(γ −1)/2γ ]

1/2

. We show in what follows that M

 1toavoid

violation of the second law of thermodynamics. The two possible solutions are: (a) no

change of state; and (b) a sudden transition from supersonic to subsonic ﬂow with

consequent increases in pressure, density, and temperature. The density, velocity, and

temperature ratios can be similarly obtained. They are

(γ + 1)M

(γ − 1)M

+ 2

, (16.33)

= 1 +

2(γ − 1)

(γ + 1)

γM

+ 1

− 1). (16.34)

The normal shock relations (16.31)–(16.34) were worked out independently by

the British engineer W. J. M. Rankine (1820–1872) and the French ballistician

Pierre Henry Hugoniot (1851–1887). These equations are sometimes known as the

Rankine–Hugoniot relations.

736 Compressible Flow

Figure 16.9 Normal shock-wave solution M

) for γ = 1.4. Trivial (no change) solution is also

shown. Asymptotes are [(γ − 1)/2γ ]

1/2

= 0.378.

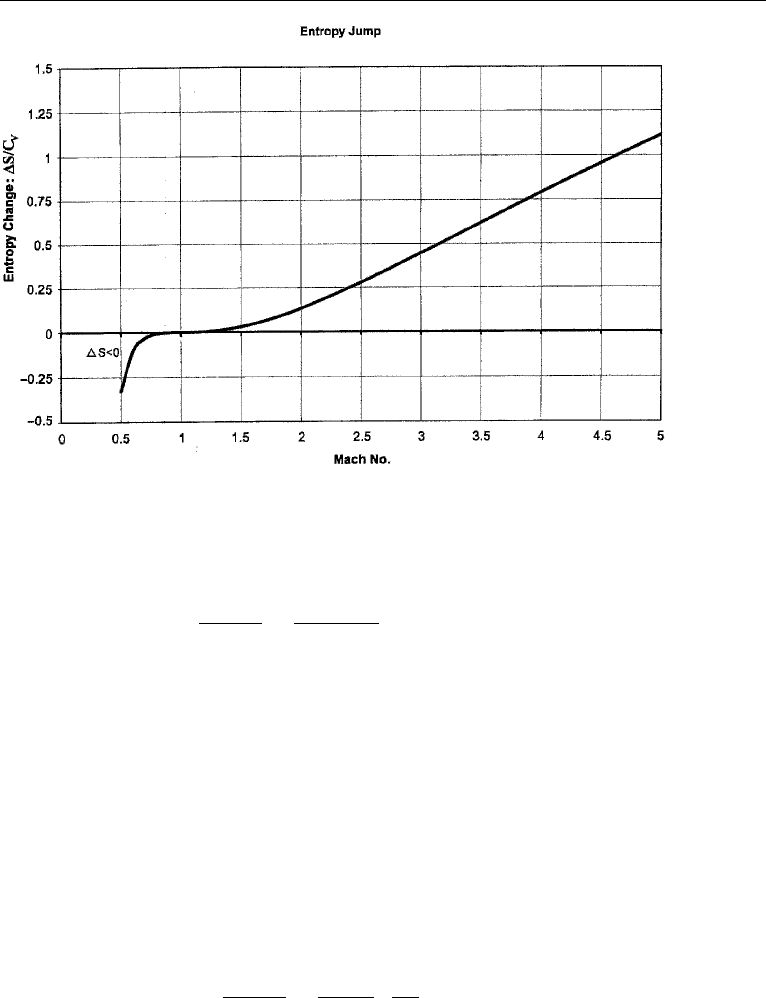
An important quantity is the change of entropy across the shock. Using equa-

tion (16.4), the entropy change is

− S

= ln









= ln



1 +

2γ

γ + 1

− 1)



(γ − 1)M

+ 2

(γ + 1)M





, (16.35)

which is plotted in Figure 16.10. This shows that the entropy across an expansion

shock would decrease, which is impermissible for the perfect gas equation of state.

However, for a heavy ﬂuorocarbon gas (FC-70), Fergason et al. (2001), using different

equations of state, have numerically simulated a rarefaction (expansion) shock in a

shock tube type ﬂow. Equation (16.36) calculates the entropy change for a perfect gas

with constant speciﬁc heats explicitly in the neighborhood of M

= 1. Now assume

that the upstream Mach number M

is only slightly larger than 1, so that M

− 1is

6. Normal Shock Wave 737

Figure 16.10 Entropy change (S

−S

)/C

as a function of M

for γ = 1.4. Note higher-order contact

at M = 1.

a small quantity. It is straightforward to show that equation (16.35) then reduces to

(Exercise 2)

− S



2γ(γ − 1)

3(γ + 1)

− 1)

. (16.36)

This shows that we must have M

> 1 because the entropy of an adiabatic

process cannot decrease. Equation (16.32) then shows that M

< 1. Thus, the

Mach number changes from supersonic to subsonic values across a normal shock;

a discontinuous change from subsonic to supersonic conditions would lead to a

violation of the second law of thermodynamics. (A shock wave is therefore anal-

ogous to a hydraulic jump (Chapter 7, Section 12) in a gravity current, in which

the Froude number jumps from supercritical to subcritical values; see Figure 7.23.)

Equations (16.31), (16.33), and (16.34) then show that the jumps in p, ρ, and T

are also from low to high values, so that a shock wave compresses and heats

a ﬂuid.

Note that the terms involving the ﬁrst two powers of (M

− 1) do not appear in

equation (16.36). Using the pressure ratio (16.31), equation (16.36) can be written as

− S



− 1

12γ



p



This shows that as the wave amplitude decreases, the entropy jump goes to zero

much faster than the rate at which the pressure jump (or the jumps in velocity

or temperature) goes to zero. Weak shock waves are therefore nearly isentropic.

738 Compressible Flow

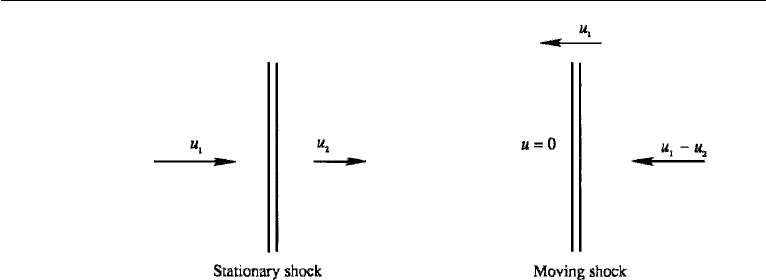
Figure 16.11 Stationary and moving shocks.

This is why we argued that the propagation of sound waves is an isentropic

process.

Because of the adiabatic nature of the process, the stagnation properties T

and

are constant across the shock. In contrast, the stagnation properties p

and ρ

decrease across the shock due to the dissipative processes inside the wavefront.

Normal Shock Propagating in a Still Medium

Frequently, one needs to calculate the properties of ﬂow due to the propagation

of a shock wave through a still medium, for example, due to an explosion. The

transformation necessary to analyze this problem is indicated in Figure 16.11. The

left panel shows a stationary shock, with incoming and outgoing velocities u

and u

respectively. On this ﬂow we add a velocity u

directed to the left, so that the ﬂuid

entering the shock is stationary, and the ﬂuid downstream of the shock is moving to

the left at a speed u

−u

, as shown in the right panel of the ﬁgure. This is consistent

with our remark in Section 2 that the passage of a compression wave “pushes” the

ﬂuid forward in the direction of propagation of the wave. The shock speed is therefore

, with a supersonic Mach number M

= u

> 1. It follows that a ﬁnite pres-

sure disturbance propagates through a still ﬂuid at supersonic speed, in contrast to

inﬁnitesimal waves that propagate at the sonic speed. The expressions for all the ther-

modynamic properties of the ﬂow, such as those given in equations (16.31)–(16.36),

are still applicable.

Shock Structure

We shall now note a few points about the structure of a shock wave. The viscous and

heat conductive processes within the shock wave result in an entropy increase across

the front. However, the magnitude of the viscosity µ and thermal conductivity k only

determines the thickness of the front and not the magnitude of the entropy increase.

The entropy increase is determined solely by the upstream Mach number as shown

by equation (16.36). We shall also see later that the wave drag experienced by a body

due to the appearance of a shock wave is independent of viscosity or thermal con-

ductivity. (The situation here is analogous to the viscous dissipation in fully turbulent

6. Normal Shock Wave 739

ﬂows (Chapter 13, Section 8), in which the dissipation rate ε is determined by the

velocity and length scales of a large-scale turbulence ﬁeld (ε ∼ u

/l) and not by the

magnitude of the viscosity; a change in viscosity merely changes the scale at which

the dissipation takes place (namely, the Kolmogorov microscale).)

The shock wave is in fact a very thin boundary layer. However, the velocity

gradient du/dx is entirely longitudinal, in contrast to the lateral velocity gradient

involved in a viscous boundary layer near a solid surface. Analysis shows that the

thickness δ of a shock wave is given by

δu

∼ 1,

where the left-hand side is a Reynolds number based on the velocity change across

the shock, its thickness, and the average value of viscosity. Taking a typical value for

air of ν ∼ 10

−5

/s, and a velocity jump of u ∼ 100 m/s, we obtain a shock

thickness of

δ ∼ 10

−7

This is not much larger than the mean free path (average distance traveled by a

molecule between collisions), which suggests that the continuum hypothesis becomes

of questionable validity in analyzing shock structure.

To gain some insight into the structure of shock waves, we shall consider the

one-dimensional steady Navier–Stokes equations, including heat conduction and

Newtonian viscous stresses. Despite the fact that the signiﬁcant length scale for the

structure pushes the limits of validity of the continuum formulation, the solution we

obtain provides a smooth transition between upstream and downstream states, looks

reasonable, and agrees with experiments and kinetic theory models for upstream Mach

numbers less than about 2. The equations for conservation of mass, momentum, and

energy are, respectively,

d(ρu)/dx = 0

ρudu/dx + dp/dx = d(µ



du/dx)/dx, µ



= 2µ + λ

ρudh/dx − udp/dx = µ



(du/dx)

+ d(kdT/dx)/dx.

By adding to the energy equation the product of u with the momentum equation, these

can be integrated once to yield,

ρu = m

mu + p − µ



du/dx = mV

m(h + u

/2) − µ



udu/dx − kdT /dx = mI,

where m, V , I are the constants of integration. These are evaluated upstream (state 1)

and downstream (state 2) where gradients vanish and yield the Rankine-Hugoniot

relations derived above. We also need the equations of state for a perfect gas with

constant speciﬁc heats to solve for the structure: h = C

T,p = ρRT . Multiplying

the energy equation by C

/k we obtain the form

(mC

/k)(C

T + u

/2) − (µ



/k)d(u

/2)/dx − d(C

T )/dx = mC

I/k.

740 Compressible Flow

This has an exact integral in the special case Pr



≡ µ



/k = 1. This was found by

Becker in 1922. If Stokes relation is assumed [(4.42)], 3λ +2µ = 0 then µ



= 4µ/3

and Pr = µC

/k = 3/4, which is quite close to the actual value for air. The Becker

integral is C

T + u

/2 = I . Eliminating all variables but u from the momentum

equation, using the equations of state, mass conservation, and the energy integral,

mu + (m/u)(R/C

)(I − u

/2) − µ



du/dx = mV .

With C

/R = γ /(γ − 1), multiplying by u/m, we obtain

−[2γ /(γ + 1)](µ



/m)udu/dx =−u

+[2γ /(γ + 1)]uV − 2I(γ − 1)/(γ + 1)

≡ (U

− U )(U − U

)

Divide by V

and let u/V = U . The equation for the structure becomes

−U(U

− U)

−1

(U − U

)

−1

dU =[(γ + 1)/2γ ](m/µ



)dx,

where the roots of the quadratic are

1,2

=[γ /(γ + 1)]{1 ±[1 − 2(γ

− 1)I /(γ

)]

1/2

the dimensionless speeds far up- and downstream of the shock. The left-hand side

of the equation for the structure is rewritten in terms of partial fractions and then

integrated to obtain

ln(U

− U) − U

ln(U − U

)]/(U

− U

)

=[(γ + 1)/(2γ)]m



dx/µ



≡[(γ + 1)/(2γ)]η

The structure is shown in Figure 16.12 in terms of the stretched coordinate

η =



(m/µ



)dx where µ



is often a strong function of temperature and thus of x.

A similar structure is obtained for all except quite small values of Pr



. In the limit



→ 0, Hayes (1958) points out that there must be a “shock within a shock” because

0.1

0.2

0.3

0.4

0 5

0.6

0.7

0.8

0.9

–10 –8 –6 –4 –2 0 2 4 6

= .848…

= .318…

Figure 16.12 Shock structure velocity proﬁle for the case U

= 0.848485, U

= 0.31818, corresponding

to M

= 2.187.

7. Operation of Nozzles at Different Back Pressures 741

heat conduction alone cannot provide the entire structure. In fact, Becker (1922)

(footnote, p. 341) credits Prandtl for originating this idea. Cohen and Moraff (1971)

provided the structure of both the outer (heat conducting) and inner (isothermal vis-

cous) shocks. The variable η is a dimensionless length scale measured very roughly

in units of mean free paths. We see that a measure of shock thickness is of the order

of 5 mean free paths.

7. Operation of Nozzles at Different Back Pressures

Nozzles are used to accelerate a ﬂuid stream and are employed in such systems as

wind tunnels, rocket motors, and steam turbines. A pressure drop is maintained across

it. In this section we shall examine the behavior of a nozzle as the exit pressure is

varied. It will be assumed that the ﬂuid is supplied from a large reservoir where the

pressure is maintained at a constant value p

(the stagnation pressure), while the

“back pressure” p

in the exit chamber is varied. In the following discussion, we

need to note that the pressure p

exit

at the exit plane of the nozzle must equal the back

pressure p

if the ﬂow at the exit plane is subsonic, but not if it is supersonic. This

must be true because sharp pressure changes are only allowed in a supersonic ﬂow.

Convergent Nozzle

Consider ﬁrst the case of a convergent nozzle shown in Figure 16.13, which examines

a sequence of states a through c during which the back pressure is gradually lowered.

For curve a, the ﬂow throughout the nozzle is subsonic. As p

is lowered, the Mach

number increases everywhere and the mass ﬂux through the nozzle also increases.

This continues until sonic conditions are reached at the exit, as represented by curve b.

Further lowering of the back pressure has no effect on the ﬂow inside the nozzle. This

is because the ﬂuid at the exit is now moving downstream at the velocity at which no

pressure changes can propagate upstream. Changes in p

therefore cannot propagate

upstream after sonic conditions are reached at the exit. We say that the nozzle at this

stage is choked because the mass ﬂux cannot be increased by further lowering of

back pressure. If p

is lowered further (curve c in Figure 16.13), supersonic ﬂow is

generated outside the nozzle, and the jet pressure adjusts to p

by means of a series

of “oblique expansion waves,” as schematically indicated by the oscillating pressure

distribution for curve c. (The concepts of oblique expansion waves and oblique shock

waves will be explained in Sections 10 and 11. It is only necessary to note here that

they are oriented at an angle to the direction of ﬂow, and that the pressure decreases

through an oblique expansion wave and increases through an oblique shock wave.)

Convergent–Divergent Nozzle

Now consider the case of a convergent–divergent passage (Figure 16.14). Completely

subsonic ﬂow applies to curve a.Asp

is lowered to p

, sonic condition is reached

at the throat. On further reduction of the back pressure, the ﬂow upstream of the

throat does not respond, and the nozzle has “choked” in the sense that it is allowing

the maximum mass ﬂow rate for the given values of p

and throat area. There is a