Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

CAUTION

䊳

Be careful not to dismiss or discard a possible solution simply because it’s negative. For

the equation is the solution (the domain here allows negative

numbers: yields as the domain). In general, when a logarithmic

equation has multiple solutions, all solutions should be checked.

Solving an exponential equation likewise involves isolating an exponential term

on one side, or writing the equation where exponential terms of like base occur on each

side. The latter case can be solved using the uniqueness property. If the exponential

base is neither 10 nor e, logarithms of base b can be used along with the change-of-

base formula to solve the equation.

EXAMPLE 4

䊳

Solving an Exponential Equation Using Base b

Solve the exponential equation. Answer in both exact form, and approximate form

to four decimal places:

Solution

䊳

given equation

add 1

The left-hand side is neither base 10 or base e, so here we chose base 4 to solve.

logarithms base 4

Property III; change-of-base property

multiply by (exact form)

approximate form

A calculator check is shown here.

Now try Exercises 37 through 40

䊳

In some cases, two exponential terms with unlike bases may be involved. In

this case, either common logs or natural logs can be used, but be sure to distinguish

between constant terms like ln 5 and variable terms like x ln 5. As with all equa-

tions, the goal is to isolate the variable terms on one side.

x ⬇ 0.5283

x ⫽

log 9

3 log 4

3 x ⫽

log 9

log 4

log

⫽ log

⫽ 9

⫺ 1 ⫽ 8

x 6 ⫺6⫺6 ⫺ x 7 0

log1⫺6 ⫺ x2⫽ 1, x ⫽⫺16

530 CHAPTER 5 Exponential and Logarithmic Functions 5–52

College Algebra Graphs & Models—

⫺5

⫺10

The equation is not factorable, and the quadratic

formula must be used.

quadratic formula

simplify

result

Substitution shows checks, but substituting

for x gives and two of

the three terms do not represent real numbers ( is an extraneous root).

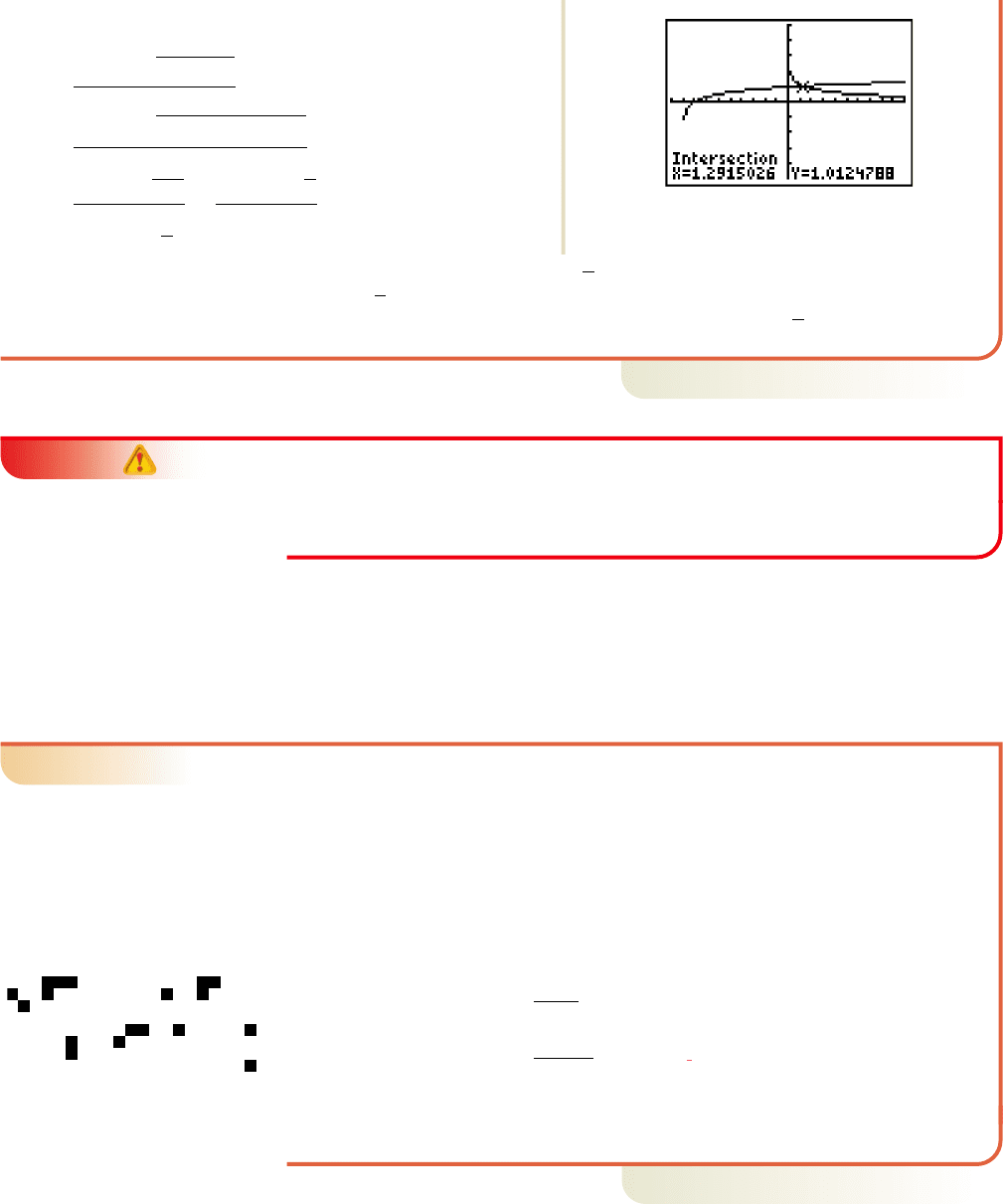
Now try Exercises 21 through 36

䊳

x ⫽⫺4 ⫺ 217

log 12.70852⫺ log 1⫺9.29152⫽ log 1⫺0.29152⫺4 ⫺ 217

x ⫽⫺4 ⫹ 217 1x ⬇ 1.291502

⫽⫺4 ⫾ 217

⫽

⫺8 ⫾ 1112

⫽

⫺8 ⫾ 417

⫽

⫺8 ⫾ 2182

⫺ 41121⫺122

2112

x ⫽

⫺b ⫾ 2b

⫺ 4ac

substitute 1 for

for

, for

⫺12

cob19545_ch05_528-538.qxd 9/2/10 9:48 PM Page 530

5–53 Section 5.5 Solving Exponential and Logarithmic Equations 531

College Algebra Graphs & Models—

EXAMPLE 5

䊳

Solving an Exponential Equation with Unlike Bases

Solve the exponential equation

Algebraic Solution

䊳

original equation

Begin by taking the natural log of both sides:

apply base-

logarithms

power property

distribute

variable terms to one side

factor out

solve for

(exact form)

approximate form

Graphical Solution

䊳

In many cases, the quality of a graphical solution depends on the ability to

determine an appropriate window size. Most often, this is accomplished using the

domain of the functions involved, the context of the application, or a few test

values. For and , we begin by observing that for ,

. However for , (see Figure 5.46). This indicates that

function values will be equal for some value of x between 0 and

1, and the window size for x must be set accordingly. These test values also show

that y need not be greater than 36, though we may elect to use a higher value for

both x and y to obtain a good window “frame.” Using the window size indicated

in Figure 5.47 reveals the solution to the equation (where the graphs intersect) is

Now try Exercises 41 through 44

䊳

As an alternative to taking the natural log of both sides directly, we can use the

properties of exponents to simplify and combine the exponential terms as follows.

original equation

product and power properties

rewrite factors; simplify

divide by , apply power property

take natural logs

solve for

The result is equivalent to our original solution: .x ⬇ 0.81528463

ln 5

ln 7.2

⫽ x

⫽ 7.22 ln 5 ⫽ x ln 7.2

5 ⫽

⫽ a

⫽ 36

⫽ 16

x⫹1

⫽ 6

Figure 5.46

⫺15

1.5

Figure 5.47

x ⬇ 0.81528463

1X2⫽ Y

1X24

7 Y

x ⫽ 2Y

7 Y

x ⫽ 0Y

⫽ 6

⫽ 5

X⫹1

0.8153 ⬇ x

ln 5

2 ln 6 ⫺ ln 5

⫽ x

ln 5 ⫽ x12 ln 6 ⫺ ln 52

ln 5 ⫽ 2x ln 6 ⫺ x ln 5

x ln 5 ⫹ ln 5 ⫽ 2x ln 6

1x ⫹ 12 ln 5 ⫽ 2x ln 6

x⫹1

2⫽ ln 16

x⫹1

⫽ 6

x⫹1

⫽ 6

cob19545_ch05_528-538.qxd 1/7/11 5:06 PM Page 531

Logarithmic equations come in many different forms, and the following ideas

summarize the basic approaches used in solving them. For this summary, recall that for

any positive real number k, log

k is a constant. Assume M, N, and X represent algebraic

expressions in x.

1. If the equation can be written in the form , use the exponential

form and algebra to solve: .

2. If the equation can be written in the form , use the uniqueness

property and algebra to solve: .

3. If the equation has an additional constant term as in constant,

move all logarithmic terms to one side and consolidate using the product or quo-

tient properties, then use the exponential form and algebra to solve:

4. If the equation has multiple logarithmic terms as in ,

consolidate logarithmic terms using the product or quotient properties, then use

the uniqueness property and algebra to solve:

Many other forms and varieties are possible.

In advanced applications, the equations used are sometimes impossible to solve

using inverse functions. This is often the case when logarithmic or exponential func-

tions are mixed with other functions (polynomial, radical, rational, etc.). In these cases

graphing and calculating technologies become indispensible tools, and the emphasis in

working towards a solution shifts more to an understanding of the domain, the graphi-

cal attributes of the functions involved, and setting an appropriate window.

EXAMPLE 6

䊳

Solving Equations Using Technology

Find all solutions to .

Solution

䊳

Begin by noting that the domain of the

function on the left, call it Y

, is all real

numbers, since this is the domain of both

and . However, the domain of

the function on the right (call it Y

) is

, and we expect that any solution(s)

to the equation must occur to the right of

, so we opt for a standard viewing

window to begin (Figure 5.48). At ﬁrst it

appears the graphs do not intersect to the

left, but our knowledge of the domain

⫺9

x ⱖ⫺9

y ⫽ 1

xy ⫽ e

x⫺8

⫽ 1x ⫹ 9

X ⫽ MN

log

X ⫽ log

1MN2

log

X ⫽ log

M ⫹ log

log

X ⫽ log

M ⫹ log

⫽ b

constant

log

b⫽ constant

log

M ⫺ log

N ⫽ constant

log

M ⫽ log

N ⫹ constant

log

M ⫽ log

N ⫹

M ⫽ N

log

M ⫽ log

constant

⫽ M

log

M ⫽ constant

532 CHAPTER 5 Exponential and Logarithmic Functions 5–54

College Algebra Graphs & Models—

⫺10

Figure 5.48

cob19545_ch05_528-538.qxd 9/2/10 9:48 PM Page 532

5–55 Section 5.5 Solving Exponential and Logarithmic Equations 533

College Algebra Graphs & Models—

indicates they must intersect near ,

since Y

and Y

are both positive. Using the

intersection-of-graphs method, we ﬁnd one

solution is . To the right, no

point of intersection is initially visible so

we extend our window to explore whether

the graphs intersect again. Using

we note the graphs indeed intersect

(Figure 5.49) and locate a second solution

at .

Now try Exercises 45 through 48

䊳

B. Applications of Logistic, Exponential, and

Logarithmic Functions

Applications of exponential and logarithmic functions take many different forms and it

would be impossible to illustrate them all. As you work through the exercises, try to adopt

a “big picture” approach, applying the general principles illustrated here to other applica-

tions. Some may have been introduced in previous sections. The difference here is that we

can now solve for the independent variable, instead of simply evaluating the relationships.

In applications involving the logistic growth of animal populations, the initial

stage of growth is virtually exponential, but due to limitations on food, space, or other

resources, growth slows and at some point it reaches a limit. In business, the same prin-

ciple applies to the logistic growth of sales or proﬁts, due to market saturation. In these

cases, the exponential term appears in the denominator of a quotient, and we “clear

denominators” to begin the solution process.

EXAMPLE 7

䊳

Solving a Logistic Equation

A small business makes a new discovery and begins an aggressive advertising

campaign, conﬁdent they can capture 66% of the market in a short period of time.

They anticipate their market share will be modeled by the function

, where M(t) represents the percentage after t days. Use this

function to answer the following.

a. What was the company’s initial market share ( )? What was their market

share 30 days later?

b. How long will it take the company to reach a 60% market share?

䊲

Algebraic Solution

a. given

substitute 0 for

simplify

result

⫽ 6

⫽ 12 ⫽

M102⫽

1 ⫹ 10e

⫺0.05102

M1t2⫽

1 ⫹ 10e

⫺0.05t

t ⫽ 0

M1t2⫽

1 ⫹ 10e

⫺0.05t

x ⬇ 11.433

Xmax ⫽ 20

x ⬇ ⫺8.994

x ⫽⫺9

⫺10

Figure 5.49

䊲

Graphical Solution

a. After entering the function as

, we can ﬁnd Y

(0) and

(30) directly on the home

screen (Figure 5.50). The

company began the ad

campaign with a 6% market

share, and 30 days later they

had secured over a 20.4%

market share.

Figure 5.50

A. You’ve just seen how we

can solve general logarithmic

and exponential equations

cob19545_ch05_528-538.qxd 11/27/10 12:39 AM Page 533

The company originally had only a 6% market share.

substitute 30 for

simplify

result

After 30 days, they held a 20.4% market share.

b. For part (b), we replace M(t) with 60 and

solve for t.

given

multiply by

divide by 60

subtract 1

divide by 10

apply base-

logarithms

Property III

solve for

(exact form)

approximate form

The company will reach a 60% market share in about 92 days.

Now try Exercises 49 and 50

䊳

⬇ 92

t ⫽

ln 0.01

⫺0.05

⫺0.05t ⫽ ln 0.01

ln e

⫺0.05t

⫽ ln 0.01

⫺0.05t

⫽ 0.01

10e

⫺0.05t

⫽ 0.1

1 ⫹ 10e

⫺0.05t

⫽ 1.1

1 ⫹ 10e

⫺0.05t

6011 ⫹ 10e

⫺0.05t

2⫽ 66

60 ⫽

1 ⫹ 10e

⫺0.05t

⬇ 20.4

⫽

1 ⫹ 10e

⫺1.5

M1302⫽

1 ⫹ 10e

⫺0.051302

534 CHAPTER 5 Exponential and Logarithmic Functions 5–56

College Algebra Graphs & Models—

b. Using the intersection-of-graphs method, we

graph Y

with to ﬁnd any point(s) of

intersection. For the window size, we reason

that after 30 days, there is only a 20.4% market

share (x must be much greater than 30), and a

60% market share is being explored (y must be

greater than 60). Using the window indicated in

Figure 5.51 reveals that a 60% market share

will be attained shortly after the 92nd day.

⫽ 60

Earlier we used the barometric equation to ﬁnd an

altitude H, given a temperature and the atmospheric (barometric) pressure in centime-

ters of mercury (cmHg). Using the tools from this section, we are now able to ﬁnd the

atmospheric pressure for a given altitude and temperature.

EXAMPLE 8

䊳

Using Logarithms to Determine Atmospheric Pressure

Suppose a group of climbers has just scaled Mt. Rainier, the highest mountain of

the Cascade Range in western Washington State. If the mountain is about 4395 m

high and the temperature at the summit is , what is the atmospheric

pressure at this altitude? The pressure at sea level is .P

⫽ 76 cmHg

⫺22.5°C

H ⫽ 130T ⫹ 80002 ln a

120

Figure 5.51

cob19545_ch05_528-538.qxd 9/2/10 9:48 PM Page 534

5–57 Section 5.5 Solving Exponential and Logarithmic Equations 535

College Algebra Graphs & Models—

䊲

Algebraic Solution

䊲

Graphical Solution

given

simplify

divide by 7325

exponential form

multiply by

approximate form ⬇ 41.7

P ⫽

0.6

⫽ 76

0.6

⫽

0.6 ⫽ ln

4395 ⫽ 7325 ln

4395 ⫽ 3301⫺22.52⫹ 80004 ln

H ⫽ 130T ⫹ 80002 ln a

To ensure that no algebraic errors are introduced, we’ll

enter the function as it appears after the substitutions

are made:

For the window size,

we reason that since

x must be between 0

and 76, and y is

equal to 4395, we

only need the ﬁrst

Quadrant and a

“frame” around the

window that allows a

clear view of the

intersection point. Using the window indicated shows that

at an altitude of 4395 m and a temperature of ,

the atmospheric pressure is about 41.7 cmHg.

⫺22.5°C

⫽ 3301⫺22.52⫹ 80004 ln a

Now try Exercises 53 and 54

䊳

Additional applications involving appreciation/depreciation, Newton’s law of cooling,

space ship velocities and more, can be found in the Exercise set. See Exercises 55

through 66.

⫺1000

6000

100

B. You’ve just seen how

we can solve applications

involving logistic, exponential,

and logarithmic functions

2. To solve the equation , we

like terms using logarithmic properties,

prior to writing the equation in form.

ln1x ⫹ 32⫺ ln x ⫽ 7

䊳

CONCEPTS AND VOCABULARY

Fill in each blank with the appropriate word or phrase. Carefully reread the section if needed.

5.5 EXERCISES

1. The expression log

x represents a term,

while the expression log

9 represents a

term.

3. If certain conditions are met, we know if

, then . This is a statement

of the property, which is valid since

logarithmic functions are -to- .

M ⫽ Nlog

M ⫽ log

4. Since the domain of is . solving

logarithmic equations will sometimes produce

roots. Checking all solutions to

logarithmic equations is a necessary step.

y ⫽ log

substitute 4395

for

, 76 for

and ⫺22.5 for

divide by

0.6

(exact form)

5. Answer true or false and explain your response:

log

1M ⫹ N2⫽ log

1M2⫹ log

1N2

6. Answer true or false and explain your response:

log

b⫽

log

cob19545_ch05_528-538.qxd 11/27/10 12:40 AM Page 535

536 CHAPTER 5 Exponential and Logarithmic Functions 5–58

College Algebra Graphs & Models—

Solve each equation and check your answers.

10.

11.

12.

13.

14.

Solve each equation using the uniqueness property.

15.

16.

17.

18.

19.

20.

Solve each equation using any appropriate method.

State solutions in both exact form and in approximate

form rounded to four decimal places. Clearly identify

any extraneous roots. If there are no solutions, so state.

21.

22.

23.

24.

25. ln1x ⫹ 72⫹ ln 9 ⫽ 2

log

1x ⫺ 42⫹ log

172⫽ 2

log

192⫹ log

1x ⫹ 32⫽ 3

log1x ⫺ 72⫹ log 3 ⫽ 2

log12x ⫺ 12⫹ log 5 ⫽ 1

1x ⫺ 12⫹ ln 6 ⫽ ln 13x2

18x ⫺ 42⫽ ln 2 ⫹ ln x

log

1x ⫹ 62⫺ log

x ⫽ log

log

1x ⫹ 22⫺ log

3 ⫽ log

1x ⫺ 12

log

12x ⫺ 32⫽ log 3

log

15x ⫹ 22⫽ log 2

log 13x ⫺ 132⫽ 2 ⫺ log x

log

12x ⫹ 12⫽ 1 ⫺ log x

log x ⫺ 1 ⫽⫺log 1x ⫺ 92

log1x ⫺ 152⫺ 2 ⫽⫺log x

log14 ⫺ 3x2⫺ log 145 ⫽⫺2

log12x ⫺ 52⫺ log 78 ⫽⫺1

log 5 ⫹ log1x ⫺ 92⫽ 1

log 4 ⫹ log1x ⫺ 72⫽ 2

26.

27.

28.

29.

30.

31.

32.

33.

34.

35. 36.

37. 38.

39. 40.

Solve each equation using the zeroes method or the

intersection-of-graphs method. Round approximate

solutions to three decimal places.

41.

42.

43.

44.

45.

46.

1 ⫹ 15e

⫺0.06x

⫽ 50

250

1 ⫹ 4e

⫺0.06x

⫽ 200

⫺ 9x ⫽

⫺x⫺6

⫽ x

⫹ x ⫺ 6

⫺ 25

⫺ 9

⫽⫺ln1x ⫹ 92⫹ 6

x ⫽ ln1x ⫹ 52

⫽ 4

2x⫺1

x⫹1

⫽ 3

⫺ 3 ⫽ 78,4625

⫺ 2 ⫽ 128,965

⫽ 35897

⫽ 231

ln x ⫹ ln1x ⫺ 22⫽ ln 4

log1x ⫺ 12⫺ log x ⫽ log1x ⫺ 32

log11 ⫺ x2⫹ log x ⫽ log1x ⫹ 42

log1⫺x ⫺ 12⫽ log15x2⫹ log x

ln 21 ⫽ 1 ⫹ ln1x ⫺ 22

ln12x ⫹ 12⫽ 3 ⫹ ln 6

log1x ⫹ 142⫺ log x ⫽ log1x ⫹ 62

log1x ⫹ 82⫹ log x ⫽ log1x ⫹ 182

ln 5 ⫹ ln1x ⫺ 22⫽ 1

䊳

DEVELOPING YOUR SKILLS

䊳

WORKING WITH FORMULAS

47. Logistic growth:

For populations that exhibit logistic growth, the

population at time t is modeled by the function

shown, where C is the carrying capacity of the

population (the maximum population that can be

supported over a long period of time), k is the

growth constant, and . Solve the

formula for t, then use the result to ﬁnd the value of

t given , and .k ⫽ 0.075C ⫽ 450, a ⫽ 8, P ⫽ 400

a ⫽

C ⫺ P102

P102

P1t2ⴝ

1 ⴙ ae

ⴚkt

48. Estimating time of death:

Using the formula shown, a forensic expert can

compute the approximate time of death for a

person found recently expired, where T is the body

temperature when it was found, T

is the (constant)

temperature of the room, T

is the body

temperature at the time of death ( ), and

h is the number of hours since death. If the body

was discovered at 9:00

. with a temperature of

, in a room at , at approximately what

time did the person expire? (Note this formula is a

version of Newton’s law of cooling.)

73°F86.2°F

⫽ 98.6°F

h ⴝⴚ3.9

lna

T ⴚ T

ⴚ T

cob19545_ch05_528-538.qxd 11/27/10 12:41 AM Page 536

5–59 Section 5.5 Solving Exponential and Logarithmic Equations 537

College Algebra Graphs & Models—

䊳

APPLICATIONS

Use the barometric equation

for exercises 49 and 50. Recall that .

49. Altitude and temperature: A sophisticated spy

plane is cruising at an altitude of 18,250 m. If the

temperature at this altitude is , what is the

barometric pressure?

50. Altitude and temperature: A large weather

balloon is released and takes altitude, pressure, and

temperature readings as it climbs, and radios the

information back to Earth. What is the pressure

reading at an altitude of 5000 m, given the

temperature is ?

51. Stocking a lake: A farmer wants to stock a private

lake on his property with catﬁsh. A specialist studies

the area and depth of the lake, along with other

factors, and determines it can support a maximum

population of around 750 ﬁsh, with growth modeled

by the function , where P(t)

gives the current population after t months. (a) How

many catﬁsh did the farmer initially put in the

lake? (b) How many months until the population

reaches 300 ﬁsh?

52. Increasing sales: After expanding their area of

operations, a manufacturer of small storage

buildings believes the larger area can support sales

of 40 units per month. After increasing the

advertising budget and enlarging the sales force,

sales are expected to grow according to the model

, where S(t) is the expected

number of sales after t months. (a) How many sales

were being made each month, prior to the expansion?

(b) How many months until sales reach 25 units per

month?

Use Newton’s law of cooling

to complete Exercises 57 and 58. Recall that water

freezes at and use . Refer to

Section 5.2, page 498 as needed.

53. Making popsicles: On a hot summer day, Sean

and his friends mix some Kool-Aid

and decide to

freeze it in an ice tray to make popsicles. If the

water used for the Kool-Aid

was and the

freezer has a temperature of , how long will

they have to wait to enjoy the treat?

54. Freezing time: Suppose the current temperature in

Esconabe, Michigan, was when a arctic

cold front moved over the state. How long would it

take a puddle of water to freeze over?

5°F47°F

⫺20°F

75°F

k ⴝⴚ0.01232ⴗF

T ⴝ T

ⴙ (T

ⴚ T

S1t2⫽

1 ⫹ 1.5e

⫺0.08t

P1t2⫽

750

1 ⫹ 24e

⫺0.075t

⫺18°C

⫺75°C

ⴝ 76 cmHg

H ⴝ 130T ⴙ 80002 ln a

Depreciation/appreciation: As time passes, the value of

certain items decrease (appliances, automobiles, etc.),

while the value of other items increase (collectibles,

real estate, etc.). The time T in years for an item to

reach a future value can be modeled by the formula

where V

is the purchase price when

new, V

is its future value, and k is a constant that

depends on the item.

55. Automobile depreciation: If a new car is purchased

for $28,500, ﬁnd its value 3 yr later if .

56. Home appreciation: If a new home in an

“upscale” neighborhood is purchased for $130,000,

ﬁnd its value 12 yr later if .

Drug absorption: The time required for a certain

percentage of a drug to be absorbed by the body after

injection depends on the drug’s absorption rate. This

can be modeled by the function T( p) , where

p represents the percent of the drug that remains

unabsorbed (expressed as a decimal), k is the absorption

rate of the drug, and T(p) represents the elapsed time.

57. For a drug with an absorption rate of 7.2%, (a) ﬁnd

the time required (to the nearest hour) for the body

to absorb 35% of the drug, and (b) ﬁnd the percent

of this drug (to the nearest half percent) that

remains unabsorbed after 24 hr.

58. For a drug with an absorption rate of 5.7%, (a) ﬁnd

the time required (to the nearest hour) for the body

to absorb 50% of the drug, and (b) ﬁnd the percent

of this drug (to the nearest half percent) that

remains unabsorbed after 24 hr.

Spaceship velocity: In space travel, the change in the

velocity of a spaceship V

(in km/sec) depends on the

mass of the ship M

(in

tons), the mass of the fuel

which has been burned M

(in tons) and the escape

velocity of the exhaust V

(in km/sec). Disregarding

frictional forces, these are

related by the equation

59. For the Jupiter VII rocket, ﬁnd the mass of the fuel

that has been burned if when

, and the ship’s mass is 100 tons.

60. For the Neptune X satellite booster, ﬁnd the mass

of the ship M

if of fuel has been

burned when and .V

⫽ 10 km/secV

⫽ 8 km/sec

⫽ 75 tons

⫽ 8 km/sec

⫽ 6 km/sec

ⴝ V

ln a

⫺ M

ⴝ

ⴚln p

k ⫽⫺16

k ⫽ 5

T ⴝ k ln

cob19545_ch05_528-538.qxd 11/27/10 12:41 AM Page 537

538 CHAPTER 5 Exponential and Logarithmic Functions 5–60

College Algebra Graphs & Models—

Learning curve: The job performance of a new

employee when learning a repetitive task (as on an

assembly line) improves very quickly at ﬁrst, then

grows more slowly over time. This can be modeled by

the function , where a and b are

constants that depend on the type of task and the

training of the employee.

61. The number of toy planes an employee can

assemble from its component parts depends on the

length of time the employee has been working.

This output is modeled by ,

where P(t) is the number of planes assembled daily

after working t days. (a) How many planes is an

P1t2⫽ 5.9 ⫹ 12.6 ln t

P(t) ⴝ a ⴙ b ln t

employee making after 5 days on the job? (b) How

many days until the employee is able to assemble

34 planes per day?

62. The number of circuit boards an associate can

assemble from its component parts depends on the

length of time the associate has been working. This

output is modeled by , where

B(t) is the number of boards assembled daily after

working t days. (a) How many boards is an

employee completing after 9 days on the job?

(b) How long will it take until the employee is able

to complete 10 boards per day?

B1t2⫽ 1 ⫹ 2.3 ln t

䊳

EXTENDING THE CONCEPT

Solve the following equations. Note that equations Exercises 63 and 64 are in quadratic form.

64. 3e

⫺ 4e

⫺ 7 ⫽⫺3

63. 2e

⫺ 7e

⫽ 15

65. Use the algebraic method to ﬁnd the inverse

function.

a. b. y ⫽ 2 ln

1x ⫺ 32f 1x2⫽ 2

x⫹1

66. Show that by composing the

functions.

b. f

1x2⫽ e

x⫺1

; g1x2⫽ ln x ⫹ 1

1x2⫽ 3

x⫺2

; g1x2⫽ log

x ⫹ 2

g1x2⫽ f

⫺1

1x2

67. Use properties of logarithms and/or exponents to

show

a. is equivalent to .

b. is equivalent to ,

where .r ⫽ ln b

y ⫽ e

y ⫽ b

y ⫽ e

x ln 2

y ⫽ 2

68. Use test values for p and q to demonstrate that the

following relationships are false.

a. b.

c. ln

b⫽

ln p

ln q

ln p ⫹ ln q ⫽ ln1p ⫹ q2ln 1pq2⫽ ln p ln q

70. (3.3) Match the graph shown

with its correct equation,

without actually graphing

the function.

71. (2.3/2.4) State the domain and range of the

functions.

a. b. y ⫽

冟

x ⫹ 2

冟

⫺ 3y ⫽ 12x ⫹ 3

y ⫽ x

⫺ 4x ⫺ 5

y ⫽⫺x

⫹ 4x ⫹ 5

y ⫽⫺x

⫺ 4x ⫹ 5

y ⫽ x

⫹ 4x ⫺ 5

72. (4.5) Graph the function . Label all

intercepts and asymptotes.

73. (2.6) Suppose the maximum load (in tons) that can

be supported by a cylindrical post varies directly

with its diameter raised to the fourth power and

inversely as the square of its height. A post 8 ft

high and 2 ft in diameter can support 6 tons. How

many tons can be supported by a post 12 ft high

and 3 ft in diameter?

1x2⫽

⫺ 4

x ⫺ 1

69. Match each equation with the most appropriate solution strategy, and justify/discuss why.

a. apply base-10 logarithm to both sides

b. rewrite and apply uniqueness property for exponentials

c. apply uniqueness property for logarithms

d. apply either base-10 or base-e logarithm

e. apply base-e logarithm

f. write in exponential form

䊳

MAINTAINING YOUR SKILLS

x⫹2

⫽ 23

5x⫺3

⫽ 32

⫽ 97

log1x

⫺ 3x2⫽ 2

log12x ⫹ 32⫽ log 53

x⫹1

⫽ 25

10⫺10

⫺10

cob19545_ch05_528-538.qxd 11/27/10 12:42 AM Page 538

5–61 539

College Algebra G&M—

Simple Interest Formula

If principal p is deposited or borrowed at interest rate r for a period of t years, the

simple interest on this account will be

The total amount A accumulated or due after this period will be

A ⫽ p ⫹ prt

A ⫽ p11 ⫹ rt2

I ⫽ prt

WORTHY OF NOTE

If a loan is kept for only a certain

number of months, weeks, or days,

the time t should be stated as a

fractional part of a year so the time

period for the rate (years) matches

the time period over which the loan

is repaid.

EXAMPLE 1

䊳

Solving an Application of Simple Interest

Many ﬁnance companies offer what have become known as PayDay Loans—a

small $50 loan to help people get by until payday, usually no longer than 2 weeks.

If the cost of this service is $12.50, determine the annual rate of interest charged by

these companies.

Solution

䊳

The interest charge is $12.50, the initial principal is $50.00, and the time period is

2 weeks or of a year. The simple interest formula yields

simple interest formula

substitute $12.50 for I, $50.00 for

, and for

solve for r

The annual interest rate on these loans is a whopping 650%!

Now try Exercises 7 through 16

䊳

6.5 ⫽ r

12.50 ⫽ 50ra

I ⫽ prt

⫽

Would you pay $750,000 for a home worth only $250,000? Surprisingly, when a con-

ventional mortgage is repaid over 30 years, this is not at all rare. Over time, the accu-

mulated interest on the mortgage is easily more than two or three times the original

value of the house. In this section we explore how interest is paid or charged, and look

at other applications of exponential and logarithmic functions from business, ﬁnance,

as well as the physical and social sciences.

A. Simple and Compound Interest

Simple interest is an amount of interest that is computed only once during the lifetime

of an investment (or loan). In the world of ﬁnance, the initial deposit or base amount is

referred to as the principal p, the interest rate r is given as a percentage and stated as

an annual rate, with the term of the investment or loan most often given as time t in

years. Simple interest is merely an application of the basic percent equation, with the

additional element of time coming into play: , or

. To ﬁnd the total amount A that has accumulated (for deposits) or is due (for

loans) after t years, we merely add the accumulated interest to the initial principal:

.A ⫽ p ⫹ prt

I ⫽ prt

interest ⫽ principal ⫻ rate ⫻ time

5.6 Applications from Business, Finance, and Science

LEARNING OBJECTIVES

In Section 5.6 you will see

how we can:

A. Calculate simple interest

and compound interest

B. Calculate interest

compounded continuously

C. Solve applications

of annuities and

amortization

D. Solve applications of

exponential growth and

decay

cob19545_ch05_539-552.qxd 9/2/10 9:49 PM Page 539