Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.

510 CHAPTER 5 Exponential and Logarithmic Functions 5–32
College Algebra Graphs & Models—
EXAMPLE 7B
䊳
Comparing Earthquake Intensity to the Reference Intensity
How many times more intense than the reference intensity I
0
was the Peruvian
earthquake of June 23, 2001, with magnitude 8.4.
Solution
䊳
magnitude equation
substitute 8.4 for
M
(
I
)
exponential form
solve for
I
The earthquake was over 251 million times more intense than the reference intensity.
EXAMPLE 7C
䊳
Comparing Earthquake Intensities
Referring to Example 7A, how many times more
intense was the Sumatra earthquake as compared
to the Eureka earthquake?
Solution
䊳
The Sumatra quake had a Richter value of 9.3,
with an intensity of 10
9.3
. Similarly, the Eureka
quake was measured at 6.5 on the Richter
scale, with an intensity of 10
6.5
. Using these
intensities, we find that the Sumatra quake was
or about 631 times more intense than the Eureka quake.
Now try Exercises 81 through 94
䊳
A second application of logarithmic functions involves the relationship between
altitude and barometric pressure. The altitude or height above sea level can be determined
by the formula , where H is the altitude in meters for a
temperature T in degrees Celsius, P is the barometric pressure at a given altitude in
units called centimeters of mercury (cmHg), and P
0
is the barometric pressure at sea
level: 76 cmHg.
EXAMPLE 8
䊳
Using Logarithms to Determine Altitude
Hikers at the summit of Mt. Shasta in northern California take a pressure reading
of 45.1 cmHg at a temperature of . How high is Mt. Shasta?
Solution
䊳
For this exercise, , and . The formula yields
given formula
substitute given values
simplify
result
Mt. Shasta is about 4316 m high.
Now try Exercises 95 through 98
䊳
⬇ 4316
8270 ln
a
76
45.1
b
330192 80004 ln
a
76
45.1
b
H 130T 80002 ln
a
P
0
P
b
T 9P
0
76, P 45.1
9°C
H 130T 80002 lna
P
0
P
b
10
9.3
10
6.5
10
2.8
10
8.4
⬇ 251,188,643 I ⬇ 251,188,643I
0
I 10
8.4
I
0
10
8.4
a
I
I
0
b
8.4 log
a
I
I
0
b
M1I2 log
a
I
I
0
b
cob19545_ch05_504-516.qxd 9/2/10 9:32 PM Page 510

5–33 Section 5.3 Logarithms and Logarithmic Functions 511
College Algebra Graphs & Models—
Our final application shows the versatility of logarithmic functions, and their value
as a real-world model. Large advertising agencies are well aware that after a new ad
campaign, sales will increase rapidly as more people become aware of the product.
Continued advertising will give the new product additional market share, but once the
“newness” wears off and the competition begins responding, sales tend to taper off—
regardless of any additional amount spent on ads. This phenomenon can be modeled
by the function
where S(d) is the number of expected sales after d dollars are spent, and a and k are
constants related to product type and market size.
EXAMPLE 9
䊳
Using Logarithms for Marketing Strategies
Market research has shown that sales of the
MusicMaster, a new system for downloading and
playing music, can be approximated by the
equation d, where S(d) is the
number of sales after d thousand dollars is spent on
advertising. The graph of is shown.
a. What sales volume is expected if the
advertising budget is $40,000?
b. If the company needs to sell 3500 units to
begin making a profit, how much should be
spent on advertising?
Solution
䊳
a. For sales volume, we simply evaluate the function for (d in thousands):
given equation
substitute 40 for
d
250 ln
Spending $40,000 on advertising will generate approximately 3422 sales.
b. To find the advertising budget needed, we substitute number of sales and solve
for d.
given equation
substitute 3500 for
S
(
d
)
subtract 2500
divide by 250
exponential form
About $54,600 should be spent in order to sell 3500 units.
Now try Exercises 99 and 100
䊳
From the graph of S(d) given in Example 10, it is apparent that while the number of
sales continues to grow as more money is spent, the rate of growth slows considerably
beyond $50,000. In cases like this a numeric view of what’s happening can be more
meaningful. Here we’ll use the TABLE feature in an entirely new way to investigate the
number of sales gained for each additional $1000 spent. For ln x,
we’ll enter , which will automatically have the calculator find
the difference between the current number of sales (spending x thousand dollars), and
the number of sales made when $1000 less is spent . Figure 5.36 shows
that initially each additional $1000 spent results in a substantial sales increase, while
Figure 5.37 shows very minor increases for a like amount spent.
1x 1 dollars2
Y
2
Y
1
1x2 Y
1
1x 12
Y
1
2500 250
e
4
⬇ 54.598 54.598 ⬇ d
e
4
d
4 ln d
1000 250 ln d
3500 2500 250 ln d
S1d2 2500 250 ln d
3422
40 ⬇ 922 ⬇ 2500 922
S1402 2500 250 ln 40
S1d2 2500 250 ln d
d 40
y S1d2
S1d2 2500 250 ln
S1d2 k a ln d
10
2000
2500
3000
3500
4000
4500
20 30 40 50 60 70 80 90 100
y
x
y 2500 250lnx
E. You’ve just seen how
we can solve applications of
logarithmic functions
cob19545_ch05_504-516.qxd 11/30/10 4:42 PM Page 511

512 CHAPTER 5 Exponential and Logarithmic Functions 5–34
College Algebra Graphs & Models—
Figure 5.36 Figure 5.37
There are a number of other interesting applications of logarithmic functions in the
Exercise set. See Exercises 101 through 106.
5.3 EXERCISES
2. The range of is all , and
the domain is . Further, as ,
.
4. The function is an increasing function if
, and a decreasing function if .
6. Explain how the graph of can be
obtained from Where is the “new”
x-intercept? Where is the new asymptote?
y log
b
x.
Y log
b
1x 32
y log
b
x
y S
x S 0
x 僆
y log
b
x
䊳
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase. Carefully reread the section if needed.
1. A logarithmic function is of the form ,
where , and inputs are
than zero.
3. For logarithmic functions of the form
the x-intercept is , since log
b
.
5. What number does the expression log
2
32
represent? Discuss/Explain how
justifies this fact.
log
2
32 log
2
2
5
1
y log
b
x,
17 0
y
䊳
DEVELOPING YOUR SKILLS
Write each equation in exponential form.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22. log 0.001 3ln 154.5982⬇ 4
log 10,000 4log 100 2
log
4
16 2log
7
49 2
1 ln e1 log
2
2
1
2
log
81
9
1
3
log
8
2
0 ln 10 log
9
1
3 ln
1
e
3
1 log
7
1
7
2 log
3
93 log
2
8
Write each equation in logarithmic form.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
33. 34.
35. 36.
37. 38. 27
2
3
1
9
4
3
2
1
8
e
3
4
⬇ 2.1174
3
2
8
10
5
1
100,000
10
2
1
100
e
1
e10
3
1000
1
1
5
2
2
251
1
3
2
3
27
8
0
1e
0
1
2
3
1
8
3
2
1
9
e
3
⬇ 20.0864
3
64
cob19545_ch05_504-516.qxd 11/27/10 12:32 AM Page 512
5–35 Section 5.3 Logarithms and Logarithmic Functions 513
College Algebra Graphs & Models—
Determine the value of each logarithm without using a
calculator.
39. log
4
4 40. log
9
9
41. log
11
121 42. log
12
144
43. ln e 44. ln e
2
45. log
4
2 46. log
81
9
47. 48.
49. 50.
Use a calculator to evaluate each expression, rounded to
four decimal places.
51. log 50 52. log 47
53. ln 1.6 54. ln 0.75
55. ln 225 56. ln 381
57. 58.
Graph each function using transformations of
and strategically plotting a few points. Clearly state the
transformations applied.
59. 60.
61. 62.
63. 64.
65. 66.
Use the transformation equation
and the asymptotes and intercept(s) of the parent
function to match each equation to one of the graphs
given. Assume b 1.
67. 68.
69. 70.
71. 72. y log
b
xy log
b
x 2
y log
b
x 1y 1 log
b
x
y 2log
b
xy log
b
1x 22
y ⴝ af 1x ⴞ h2ⴞ k
Y
2
ln x 2Y
1
ln1x 12
r
1x2 ln1x 12 2q1x2 ln1x 12
p1x2 log
3
x 2h1x2 log
2
1x 22 3
g1x2 log
2
1x 22f 1x2 log
2
x 3
y ⴝ log
b
x
log 4log 137
ln
1
1e
ln
1
e
2
log
9
1
81
log
7
1
49
Determine the domain of the following functions.
73. 74.
75. 76.
77. 78. y ln19x x
2
2y log19 x
2
2
y ln15 3x
y log
5
12x 3
y ln a
x 2
x 3
by log
6
a
x 1
x 3
b
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
x
y
54321
54321
1
2
3
4
5
2
3
4
5
1
I. II.
IV.
V. V I .
III.
䊳
WORKING THE FORMULAS
79. pH level:
The pH level of a solution indicates the concentration
of hydrogen ions in a unit called moles per
liter. The pH level f(x) is given by the formula shown
(often written as pH log[H
]), where x is the
ion concentration (given in scientific notation). A
solution with is called an acid (lemon juice:
and a solution with is called a
base (household ammonia: Use the
formula to determine the pH level of tomato juice if
moles per liter. Is this an acid or
base solution?
x 7.94 10
5
pH ⬇ 112.
pH 7 7pH ⬇ 22,
pH 6 7
1H
2
f
1x2ⴝⴚlog x
80. Time required for an investment to double:
The time required for an investment to double in
value is given by the formula shown, where T(r)
represents the time required for an investment to
double if invested at interest rate r (expressed as a
decimal). How long would it take an investment to
double if the interest rate were (a) 5%, (b) 8%,
(c) 12%?
T1r2ⴝ
log 2
log11 ⴙ r2
cob19545_ch05_504-516.qxd 11/30/10 6:10 PM Page 513

514 CHAPTER 5 Exponential and Logarithmic Functions 5–36
College Algebra Graphs & Models—
䊳
APPLICATIONS
Earthquake intensity: Use the information provided in
Example 8 to answer the following.
81. Find the value of M(I) given
a. b.
82. Find the intensity I of the earthquake given
a. b.
Determine how many times more intense the first quake
was compared to the second.
83. Great Chilean quake (1960): magnitude 9.5
Kobe, Japan, quake (1995): magnitude 6.9
84. Northern Sumatra (2004): magnitude 9.1
Southern Greece (2008): magnitude 4.5
85. Earthquake intensity: On June 25, 1989, an
earthquake with magnitude 6.2 shook the southeast
side of the Island of Hawaii (near Kalapana),
causing some $1,000,000 in damage. On October
15, 2006, an earthquake measuring 6.7 on the
Richter scale shook the northwest side of the
island, causing over $100,000,000 in damage. How
much more intense was the 2006 quake?
86. Earthquake intensity: The most intense
earthquake of the modern era occurred in Chile on
May 22, 1960, and measured 9.5 on the Richter
scale. How many times more intense was this
earthquake, than the quake that hit Northern
Sumatra (Indonesia) on March 28, 2005, and
measured 8.7?
Brightness of a star: The brightness or intensity I
of a star as perceived by the naked eye is measured
in units called magnitudes. The brightest stars have
magnitude 1 and the dimmest have
magnitude 6 The magnitude of a star
is given by the equation
where I is the actual intensity of light from the
star and I
0
is the faintest light visible to the human
eye, called the reference intensity. The intensity
I is often given as a multiple of this reference
intensity.
87. Find the value of M(I) given
a. and b.
88. Find the intensity I of a star given
a. and b. M1I2 5.2.M1I2 1.6
I 85I
0
.I 27I
0
M1I2 6 2.5
#
log a
I
I
0
b,
3M1I2 64.
3M1I2 14
M1I2 8.1.M1I2 3.2
I 75,000,000 I
0
.I 50,000I
0
Intensity of sound: The intensity of sound as
perceived by the human ear is measured in units
called decibels (dB). The loudest sounds that can
be withstood without damage to the eardrum are in
the 120- to 130-dB range, while a whisper may
measure in the 15- to 20-dB range. Decibel measure
is given by the equation where
I is the actual intensity of the sound and I
0
is the
faintest sound perceptible by the human ear—called the
reference intensity. The intensity I is often given as a
multiple of this reference intensity, with the constant
(watts per cm
2
; W/cm
2
) used as the threshold
of audibility.
89. Find the value of D(I) given
a. and b.
90. Find the intensity I of the sound given
a. and b.
Determine how many times more intense the first sound
is compared to the second.
91. pneumatic hammer: 11.2 bels
heavy lawn mower: 8.5 bels
92. train horn: 7.5 bels
soft music: 3.4 bels
93. Sound intensity of a hair dryer: Every morning
(it seems), Jose is awakened by the mind-jarring,
ear-jamming sound of his daughter’s hair dryer
(75 dB). He knew he was exaggerating, but told
her (many times) of how it reminded him of his
railroad days, when the air compressor for the
pneumatic tools was running (110 dB). In fact, how
many times more intense was the sound of the air
compressor compared to the sound of the hair
dryer?
94. Sound intensity of a busy street: The decibel level
of noisy, downtown traffic has been estimated at
87 dB, while the laughter and banter at a loud party
might be in the 60 dB range. How many times more
intense is the sound of the downtown traffic?
The barometric equation was
discussed in Example 9.
95. Temperature and atmospheric pressure:
Determine the height of Mount McKinley (Alaska),
if the temperature at the summit is , with a
barometric reading of 34 cmHg.
10°C
H ⴝ 130T ⴙ 80002 lna
P
0
P
b
D1I2 125.D1I2 83
I 10
4
.I 10
14
10
16
D1I2 10 log a
I
I
0
b,
cob19545_ch05_504-516.qxd 11/27/10 12:32 AM Page 514

5–37 Section 5.3 Logarithms and Logarithmic Functions 515
College Algebra Graphs & Models—
96. Temperature and atmospheric pressure:A
large passenger plane is flying cross-country. The
instruments on board show an air temperature of
, with a barometric pressure of 22 cmHg. What
is the altitude of the plane?
97. Altitude and atmospheric pressure: By
definition, a mountain pass is a low point between
two mountains. Passes may be very short with
steep slopes, or as large as a valley between two
peaks. Perhaps the highest drivable pass in the
world is the Semo La pass in central Tibet. At its
highest elevation, a temperature reading of
was taken, along with a barometer reading of
39.3 cmHg. (a) Approximately how high is the
Semo La pass? (b) While traveling up to this pass,
an elevation marker is seen. If the barometer
reading was 47.1 cmHg at a temperature of ,
what height did the marker give?
98. Altitude and atmospheric pressure: Hikers on
Mt. Everest take successive readings of 35 cmHg at
and 30 cmHg at . (a) How far up the
mountain are they at each reading? (b) Approximate
the height of Mt. Everest if the temperature at the
summit is and the barometric pressure is
22.2 cmHg.
99. Marketing budgets:An advertising agency has
determined the number of items sold by a certain
client is modeled by the equation
, where N(A) represents
the number of sales after spending A thousands of
dollars on advertising. Determine the approximate
number of items sold on an advertising budget of
(a) $10,000; (b) $50,000. (c) Use the TABLE
feature of a calculator to estimate how large a
budget is needed (to the nearest $500 dollars) to
sell 3000 items.
100. Sports promotions: The accountants for a major
boxing promoter have determined that the number
of pay-per-view subscriptions sold to their
championship bouts can be modeled by the
function , where N(d)
represents the number of subscriptions sold after
spending d thousand dollars on promotional
activities. Determine the number of subscriptions
sold if (a) $50,000 and (b) $100,000 is spent.
(c) Determine how much should be spent (to the
nearest $1000 dollars) to sell over 50,000
subscriptions by simplifying the logarithmic
equation and writing the result in exponential form.
101. Home ventilation: In the construction of new
housing, there is considerable emphasis placed on
correct ventilation. If too little outdoor air enters a
home, pollutants can sometimes accumulate to
levels that pose a health risk. For homes of various
sizes, ventilation requirements have been
N1d2⫽ 15,000 ⫹ 5850 ln d
N1A2⫽ 1500 ⫹ 315 ln A
⫺27°C
⫺10°C5°C
12°C
8°C
3°C
established and are based on floor area and the
number of bedrooms. For a three-bedroom home,
the relationship can be modeled by the function
, where C(x) represents the
number of cubic feet of air per minute (cfm) that
should be exchanged with outside air in a home with
floor area x (in square feet). (a) How many cfm of
exchanged air are needed for a three-bedroom home
with a floor area of 2500 ft
2
? (b) If a three-bedroom
home is being mechanically ventilated by a system
with 40 cfm capacity, what is the square footage of
the home, assuming it is built to code?
102. Runway takeoff
distance: Many
will remember the
August 27, 2006,
crash of a
commuter jet at
Lexington’s Blue
Grass Airport, that
was mistakenly trying to take off on a runway that
was just too short. Forty-nine lives were lost. The
minimum required length of a runway depends on
the maximum allowable takeoff weight (mtw) of a
specific plane. This relationship can be approximated
by the function , where
L(x) represents the required length of a runway in
feet, for a plane with x mtw in pounds.
a. The Airbus-320 has a 169,750 lb mtw. What
minimum runway length is required for takeoff?
b. By simplifying the logarithmic equation that
results and writing the equation in exponential
form, determine the mtw of a Learjet 30, which
requires a runway of 5550 ft to takeoff safely.
Memory retention: Under certain conditions, a person’s
retention of random facts can be modeled by the equation
where P(x) is the percentage of
those facts retained after x number of days. Find the
percentage of facts a person might retain after x days for the
values given. Note that many of the values given are powers
of 2. Use the change-of-base formula those that are not.
103. a. 1 day b. 4 days c. 16 days
104. a. 32 days b. 64 days c. 78 days
105. pH level: Use the formula given in Exercise 79 to
determine the pH level of black coffee if
moles per liter. Is black coffee
considered an acid or base solution?
106. Tripling time: The length of time required for an
amount of money to triple is given by the formula
(see Exercise 80). Use the
TABLE feature of a graphing calculator to help
estimate what interest rate is needed for an
investment to triple in nine years.
log 3
log11 ⫹ r2
T1r2⫽
x ⫽ 5.1 ⫻ 10
⫺5
P1x2⫽ 95 ⫺ 14 log
2
x,
L1x2⫽ 2085 ln x ⫺ 14,900
C1x2⫽ 42 ln x ⫺ 270
cob19545_ch05_504-516.qxd 1/7/11 5:01 PM Page 515
516 CHAPTER 5 Exponential and Logarithmic Functions 5–38
College Algebra Graphs & Models—
107. Many texts and reference books give estimates of
the noise level (in decibels dB) of common sounds.
Through reading and research, try to locate or
approximate where the following sounds would fall
along this scale. In addition, determine at what point
pain or ear damage begins to occur.
a. threshold of audibility b. lawn mower
c. whisper d. loud rock concert
e. lively party f. jet engine
108. Determine the value of x that makes the equation
true:
109. Find the value of each expression without using a
calculator.
a. b. c. log
0.25
32
110. Suppose you and I represent two different numbers.
Is the following cryptogram true or false? The log
of me base me is one and the log of you base you is
one, but the log of you base me is equal to the log
of me base you turned upside down.
log
4
9
27
8
log
64
1
16
log
3
3log
3
1log
3
x24⫽ 0.
䊳
EXTENDING THE CONCEPT
䊳
MAINTAINING YOUR SKILLS
111. (2.2) Graph by shifting the
parent function. Then state the domain and range
of g.
112. (R.4) Factor the following expressions:
a. b.
c. d.
113. (4.2/4.6) For the graph
shown, write the solution
set for Then write
the equation of the graph in
factored form and in
polynomial form.
f
1x26 0.
2b
2
⫺ 7b ⫹ 6n
2
⫺ 10n ⫹ 25
a
2
⫺ 49x
3
⫺ 8
g1x2⫽ 2
3
x ⫹ 2 ⫺ 1
114. (2.1) A function f(x) is defined by the ordered pairs
shown in the table. Is the function (a) linear?
(b) increasing? Justify your answers.
x
y
108642⫺10⫺8⫺6⫺4⫺2
⫺20
⫺40
⫺60
⫺80
40
60
80
100
120
20
xy
0
⫺72⫺4
⫺50⫺5
⫺18⫺6
⫺8⫺8
⫺2⫺9
⫺10
Logarithmic and exponential expressions have several fundamental properties that
enable us to solve some basic equations. In this section, we’ll learn how to use these
relationships effectively, and introduce additional properties that enable us to simplify
more complex equations before relying on the same fundamental properties to com-
plete the solution.
A. Solving Equations Using the Fundamental
Properties of Logarithms
In Section 5.3, we converted expressions from exponential form to logarithmic form
using the basic definition: . This relationship reveals the follow-
ing fundamental properties:
x ⫽ b
y
3 y ⫽ log
b
x
LEARNING OBJECTIVES
In Section 5.4 you will see
how we can:
A. Solve logarithmic
equations using the
fundamental properties
of logarithms
B. Apply the product,
quotient, and power
properties of logarithms
C. Apply the change-of-base
formula
D. Solve applications using
properties of logarithms
5.4 Properties of Logarithms
cob19545_ch05_504-516.qxd 11/30/10 4:49 PM Page 516

5–39 Section 5.4 Properties of Logarithms 517
College Algebra Graphs & Models—
Fundamental Properties of Logarithms
For any base ,
I. , since III. , since
II. , since IV. , since
To see the verification of Property IV more clearly, again note that for
is the exponential form, and substituting log
b
xfor y yields
Also note that Properties III and IV demonstrate that and are inverse
functions. In common language, “a base-b logarithm undoes a base-b exponential,”
and “a base-b exponential undoes a base-b logarithm.” For and
, using a composition verifies the inverse relationship just as in Example 5
from Section 5.1:
These properties can be used to solve basic equations involving logarithms and expo-
nentials. From the uniqueness property for exponents (page 496), note that if
, then , and we say that we have exponentiated both sides.
EXAMPLE 1
䊳
Solving Basic Logarithmic Equations
Solve each equation by applying fundamental properties. Answer in exact form and
approximate form using a calculator (round to 1000ths).
a. b.
Solution
䊳
a. given b. given
exponentiate both sides exponentiate both sides
Property IV, exact form Property IV, exact form
approximate form approximate form
Now try Exercises 7 through 10
䊳
Note that checking the exact solutions by
substitution is a direct application of Property III
(Figure 5.38).
Also, we observe that exponentiating both sides
of the equation produces the same result as simply
writing the original equation in exponential form, and
the process can be viewed in terms of either
approach.
EXAMPLE 2
䊳
Solving Basic Exponential Equations
Solve each equation by applying fundamental properties. Answer in exact form and
approximate form using a calculator (round to 1000ths).
a. b.
Solution
䊳
a. given b. given
use natural log use common log
Property III, exact form Property III, exact form
approximate form approximate form
Now try Exercises 11 through 14
䊳
x 0.915 x 5.118
x ⫽ log 8.223 x ⫽ ln 167
log 10
x
⫽ log 8.223 ln e
x
⫽ ln 167
10
x
⫽ 8.223 e
x
⫽ 167
10
x
⫽ 8.223e
x
⫽ 167
0.302 x 7.389
10
⫺0.52
⫽ x x ⫽ e
2
10
⫺0.52
⫽ 10
log x
e
ln x
⫽ e
2
⫺0.52 ⫽ log x ln x ⫽ 2
⫺0.52 ⫽ log xln x ⫽ 2
b
log
b
x
⫽ b
k
log
b
x ⫽ k
⫽ x ⫽ x
⫽ b
log
b
x
⫽ log
b
b
x
1 f
⫺1
ⴰ f 21x2⫽ f
⫺1
3
f 1x24 1 f ⴰ f
⫺1
21x2⫽ f 3 f
⫺1
1x24
f
⫺1
1x2⫽ b
x
f 1x2⫽ log
b
x
y ⫽ b
x
y ⫽ log
b
x
b
log
b
x
⫽ x.y ⫽ log
b
x,
b
y
⫽ x
log
b
x ⫽ log
b
xb
log
b
x
⫽ x 1x 7 02b
0
⫽ 1log
b
1 ⫽ 0
b
x
⫽ b
x
log
b
b
x
⫽ xb
1
⫽ blog
b
b ⫽ 1
b 7 0, b ⫽ 1
Figure 5.38
cob19545_ch05_517-527.qxd 11/27/10 12:34 AM Page 517
518 CHAPTER 5 Exponential and Logarithmic Functions 5–40
College Algebra Graphs & Models—
Similar to our observations from Example 1, taking
the logarithm of both sides produced the same result
as writing the equation in logarithmic form, and the
process can be viewed in terms of either approach.
Also note that here, checking the exact solution by
substitution is a direct application of Property IV
(Figure 5.39).
If an equation has a single logarithmic or expo-
nential term (base 10 or base e), the equation can be
solved by isolating this term and applying one of the
fundamental properties as in Examples 1 and 2.
EXAMPLE 3
䊳
Solving Exponential Equations
Solve each equation. Write answers in exact form and approximate form to four
decimal places.
a. b.
Solution
䊳
a. given
add 29
Since the left-hand side is base 10, we apply the common logarithm.
take the common log of both sides
Property III (exact form)
approximate form
b. given
add 5
divide by 3
Since the left-hand side is base e, we apply the natural logarithm.
take the natural log of both sides
Property III
solve for
x
(exact form)
approximate form
Now try Exercises 15 through 20
䊳
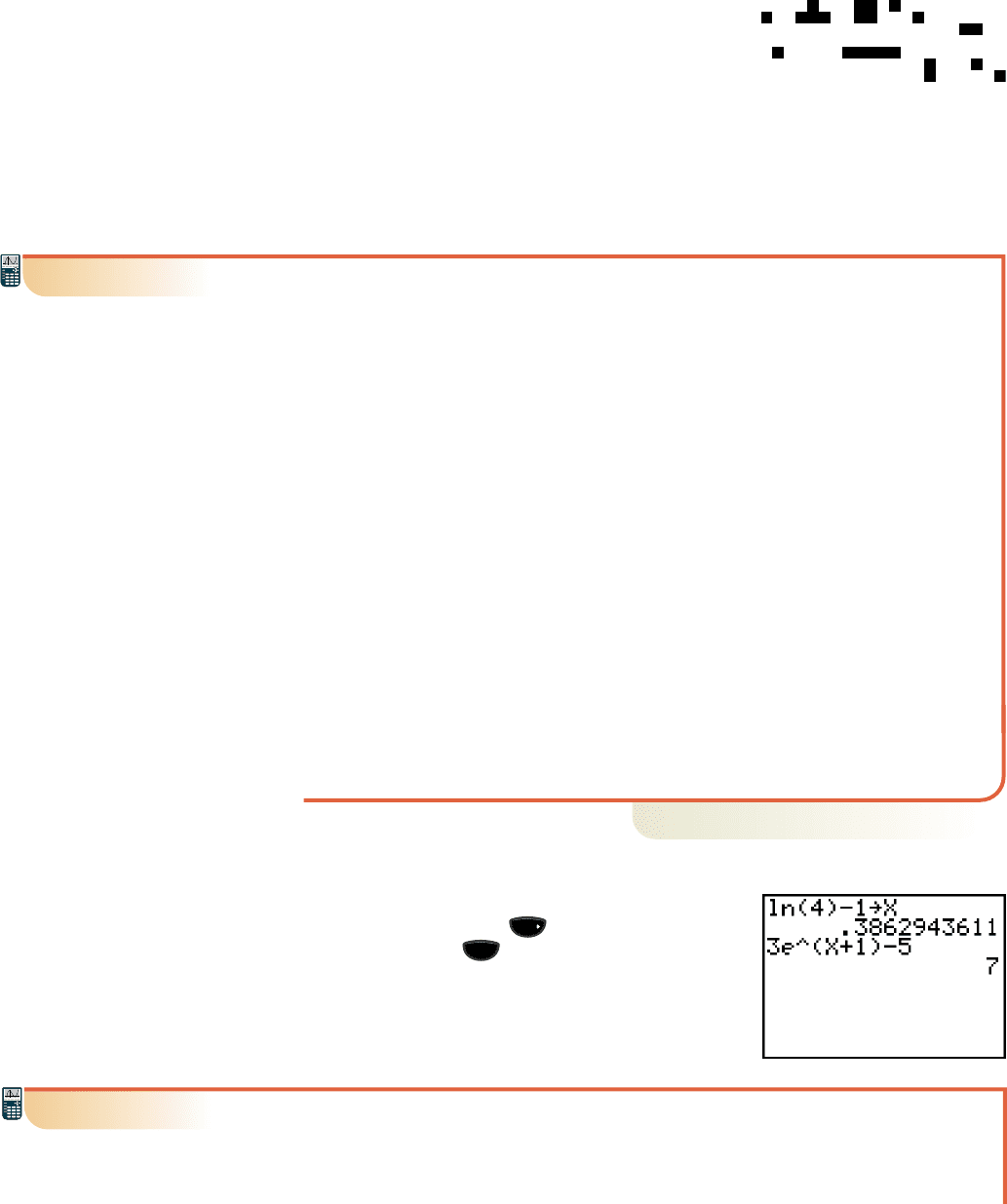
As an alternative to using the exact form to
check solutions, we can (store) the exact result
in storage location (the function variable x) and
simply enter the original equation on the home
screen. The verification for Example 3b is shown in
Figure 5.40.
EXAMPLE 4
䊳
Solving Logarithmic Equations
Solve each equation. Write answers in exact form and approximate form to four
decimal places.
a. b. ⫺4 ln 1x ⫹ 12⫺ 5 ⫽ 72 log 17x2⫹ 1 ⫽ 4
X,T,,n
STO
0.3863
x ⫽ ln 4 ⫺ 1
x ⫹ 1 ⫽ ln 4
ln e
x⫹1
⫽ ln 4
e
x⫹1
⫽ 4
3 e
x⫹1
⫽ 12
3 e
x⫹1
⫺ 5 ⫽ 7
1.9031
x ⫽ log 80
log 10
x
⫽ log 80
10
x
⫽ 80
10
x
⫺ 29 ⫽ 51
3e
x⫹1
⫺ 5 ⫽ 710
x
⫺ 29 ⫽ 51
Figure 5.39
Figure 5.40
cob19545_ch05_517-527.qxd 9/2/10 9:38 PM Page 518

5–41 Section 5.4 Properties of Logarithms 519
College Algebra Graphs & Models—
Solution
䊳
a. given
subtract 1
divide by 2
exponential form
divide by 7 (exact form)
approximate form
b. given
add 5
divide by ⫺4
exponential form
subtract 1 (exact form)
approximate form
Now try Exercises 21 through 26
䊳
As with other kinds of equations, solutions to log-
arithmic and exponential equations can be found
using the intersection-of-graphs method or the
zeroes method. For Example 4a and the intersec-
tion method, enter and
on the screen (from the domain of
the function and the expected result, we know
to set a window that includes only Quadrant I).
Using the (CALC) 5:intersect option,
we press three times to identify each curve
and bypass the “Guess” option. The calculator then finds the point of intersection and
prints it at the bottom of the screen, and verifies our calculated result.
B. The Product, Quotient, and Power Properties of Logarithms
Generally speaking, equation solving involves simplifying the equation, isolating a
variable term on one side, and applying an inverse to solve for the unknown. For loga-
rithmic equations such as , we must find a way to combine the
terms on the left, before we can work toward a solution. This requires a further explo-
ration of logarithmic properties.
Due to the close connection between exponents and logarithms, their properties
are very similar. To illustrate, we’ll use terms that can all be written in the form 2
x
, and
write the equations , and in both exponential form and loga-
rithmic form.
The exponents from a exponential form:
product are added: logarithmic form:
The exponents from a exponential form:
quotient are subtracted:
logarithmic form:
The exponents from a exponential form:
power are multiplied: logarithmic form:
Each illustration can be generalized and applied with any base b.
log
2
8
2
⫽ 2
#
log
2
8
12
3
2
2
⫽ 2
3
#
2
log
2
a
8
4
b⫽ log
2
8 ⫺ log
2
4
2
3
2
2
⫽ 2
3⫺2
log
2
18
#
42⫽ log
2
8 ⫹ log
2
4
2
3
#
2
2
⫽ 2
3⫹2
8
2
⫽ 648
#
4 ⫽ 32,
8
4
⫽ 2
log x ⫹ log 1x ⫹ 32⫽ 1
ENTER
TRACE
2nd
Y=
Y
2
⫽ 4
Y
1
⫽ 2 log17X2⫹ 1
⫺0.9502
x ⫽ e
⫺3
⫺ 1
x ⫹ 1 ⫽ e
⫺3
ln 1x ⫹ 12⫽⫺3
⫺4 ln 1x ⫹ 12⫽ 12
⫺4 ln 1x ⫹ 12⫺ 5 ⫽ 7
4.5175
x ⫽
10
3
2
7
7 x ⫽ 10
3
2
log 17x2⫽
3
2
2 log 17x2⫽ 3
2 log 17x2⫹ 1 ⫽ 4
0
10
010
Figure 5.41
A. You’ve just seen how
we can solve logarithmic
equations using the
fundamental properties of
logarithms
cob19545_ch05_517-527.qxd 9/2/10 9:38 PM Page 519
