Цивин М.Н. Конспект лекций по курсу Техническая механика жидкости. Курс с применением MATHCAD

Подождите немного. Документ загружается.

Так как гидростатическое давление р зависит только от трех незави-

симых переменных координат x, y и z , левая часть этого равенства пред-

ставляет собой полный дифференциал функции p=f(x,y,z):

dp dx dy dz

∂

∂∂

=++

∂∂∂

Делая подстановку, находим окончательно

Данное уравнение называется

основным дифференциальным

уравнением гидростатики

, так как его использование позволяет ре-

шать основные задачи гидростатики.

Рассмотрим жидкость, находящуюся в покое относительно неинер-

ционной системы координат x, y и z. В случае равновесия жидкости в поле

земного тяготения X=0, Y=0, а Z=-g. Поэтому основное уравнение полу-

чим в виде

.dp gdz

−

Произведение g

= , где γ – удельный вес данной жидкости.

Делая подстановку и разделив обе части данного уравнения на γ, пе-

репишем уравнение в следующем виде:

и, интегрируя, найдем (при γ=const)

Чтобы определить постоянную интегрирования С, рассмотрим ре-

зервуар, наполненный водой, со свободной поверхностью (атмосферное

давление)

Тогда для точки А, лежащей на поверхности, p=p

и z=z

. После под-

становки и несложного преобразования находим, что произвольная посто-

янная интегрирования равна

тогда

или

(

)

.dp Xdx Ydy Zdz

=++

(2.10)

zCConst

+= =

(2.11)

γγ

(2.12)

(

)

pzz

+−

(2.13)

Данное уравнение называют

основным уравнением гидроста-

тики

Так как разность (z

-z) представляет собой глубину погружения рас-

сматриваемой точки под уровень свободной поверхности, то уравне-

ние(2.13) может быть записано так

где

p – абсолютное давление в точке;

– поверхностное давление;

h – часть абсолютного давления p, которая обусловлена весом са-

мой жидкости.

Величина

p называется абсолютным давлением в точке и равно сум-

ме поверхностного давления и весового давления.

Уравнение (2.14) является математическим выражением закона Пас-

каля.

Определение 19.

Закон Паскаля

на сколько увеличивается поверх-

ностное давление

, на столько же

должно увеличится и абсолютное

давление в данной точке

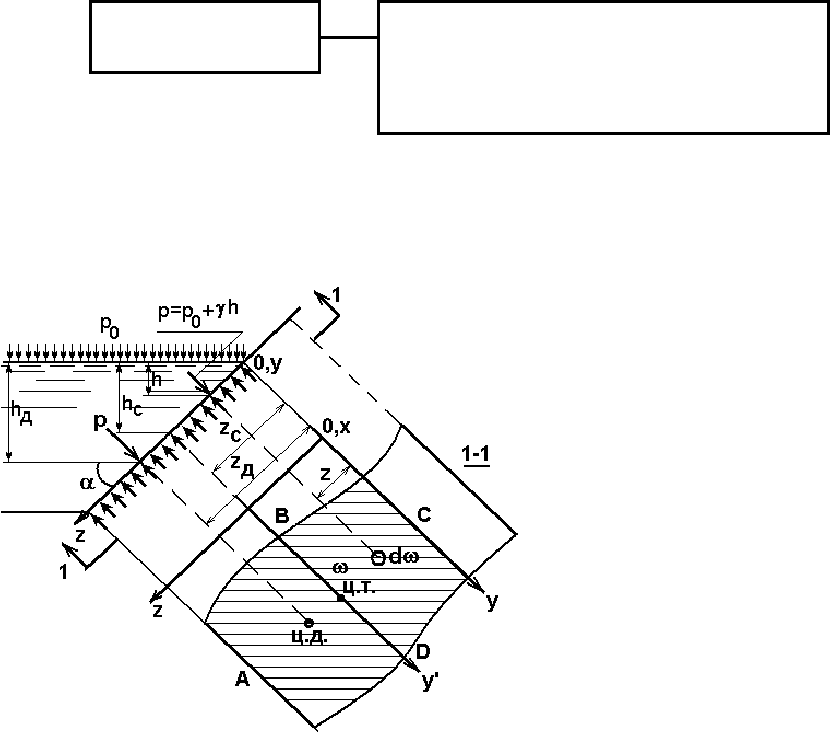
2.4. Сила гидростатического давления действующая на

плоскую фигуру любой формы

Рассмотрим давление

жидкости на плоскую стен-

ку, наклоненную к горизон-

ту под углом

α. Давление на

поверхности жидкости р

Расположим систему коор-

динат, так как показано на

развертке поверхности про-

извольной формы ABCD.

Центр тяжести элементар-

ной площадки dω, выделен-

ной на поверхности, погру-

женной под уровень свобод-

ной поверхности на глубину

h, испытывает воздействие

гидростатического давления

р. Тогда сила полного гидростатического давления, действующая на эле-

ментарную площадку,

составит

(2.14)

Рис. 2.5.

,dP pd

(2.15)

Гидростатическое давление в соответствии с данными рис.5. равно:

Подставляя это значение р в уравнение(2.15) и интегрируя его, полу-

чаем:

Интеграл

zd S

∫

представляет собой статический момент площа-

ди смоченной поверхности

ABCD относительно оси у. Обозначая ординату

центра тяжести смоченной поверхности

ABCD через z

, находим глубину

погружения этого центра

Тогда статический момент площади смоченной поверхности

ABCD

составит:

и окончательно получим

Выражение

0 c

+ есть полное гидростатическое давление в центре

тяжести смоченной поверхности

ABCD.

Следовательно:

Определение 20.

Сила гидростатического дав-

ления (абсолютного или

избыточного), действующая на

плоскую фигуру любой формы

равна площади этой фигуры,

умноженной на соответст-

вующее гидростатическое

давление (абсолютное или

избыточное) в центре тяже-

сти этой фигуры

2.5. Положение центра избыточного давления

Определение 21.

Центр избыточного давления

точка приложения силы из-

быточного давления

Положение центра избыточного давления можно определить из ус-

ловия равенства суммы моментов составляющих силы избыточного давле-

ния относительно какой-либо оси моменту равнодействующей силы дав-

ления относительно той же оси.

sin .pp hp z

γα

=+=+

(2.16)

sin .Pp zd

γα ω

∫

(2.17)

sin .

(2.18)

sin

(2.19)

(

)

Pp h

(2.20)

Предположим, что центр избыточного давления (ц.д.) расположен на

развертке поверхности в точке с ординатой z

(см.Рис. 2.5.). Момент рав-

новесия силы давления относительно оси у, равен

Момент составляющих силы давления относительно той же оси оп-

ределяется зависимостью

Здесь избыточное давление в центре элементарной площадки dω со-

ставляет γh (h – глубина погружения этого центра, равная zsin

), а момент

инерции I

составляет

∫

(относительно оси у).

Приравнивая выражения (2.21) и (2.22), получаем:

отсюда

Момент инерции I

относительно оси у можно выразить через мо-

мент инерции I

относительно оси у', проходящей через центр тяжести

смоченной поверхности ABCD:

Подставляя это значение I

в уравнение (2.24), получим

Следовательно, центр избыточного давления расположен ниже цен-

тра тяжести смоченной поверхности.

2.6. Основные случаи давления на плоские фигуры

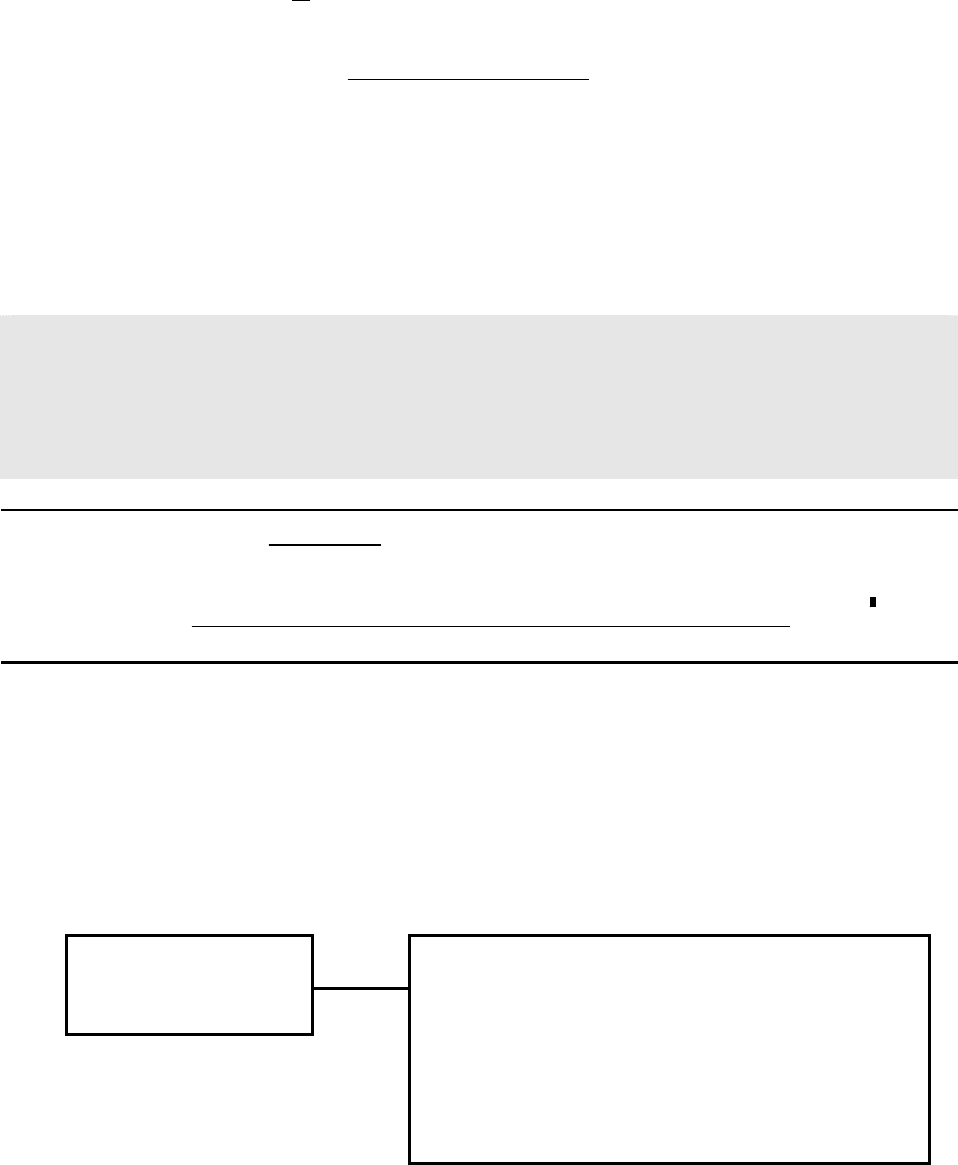
A. Трапецеидальная стенка, заглубленная под уровень воды

Рассмотрим подвергающуюся давлению воды трапецеидальную

стенку высотой l. Верхнее основание этой площадки В погружено под сво-

бодную поверхность на глубину h

, а нижнее основание b - на глубину Н.

Площадка составляет с горизонтом угол α. Силу избыточного гидростати-

ческого давления и местоположение центра давления можно определить

по следующим зависимостям

Подробный вывод, приведенных в данном параграфе зависимостей, дан в [2]

д c д

Pz h z

(2.21)

(

)

sin sin .

Mpdzhzd zdI

ωω ω

γωγα ωγ α

=== =

∫∫ ∫

(2.22)

sin ,

c д y

hz I

ωγ α

(2.23)

sin .

(2.24)

(2.25)

д c

(2.26)

При

α<90

и h

B. Прямоугольная стенка (b=B)

При α<90

и h

C. Треугольная пластинка (b=0)

При α<90

и h

D. Круглая пластина диаметром d=2r.

При α=90

и h

При

α=90

и h

E. Полукруглая пластина диаметром d=2r.

При α=90

и h

(

)

()()

()

()( ) ()

()()

000

22;

6sin

3356

22 2sin

PhBbhBb

hHBbhB b hBb

hb B HB b

−

=+++

⎡⎤

⎣⎦

−+++++

⎡⎤

⎣⎦

++ +⎡⎤

⎣⎦

(2.27)

()

6sin

2sin 2

PBb

HB b

(2.28)

(

)

()

;

2sin

3sin

Hhb

Hh h

−

=⋅

(2.29)

(

)

()

6sin

22sin

PHhB

HHhh

−

(2.30)

(

)

()

;

дд

Prrh

zhhr

γπ

==++

(2.31)

;

дд

zh r

γπ

(2.32)

Ниже приведен листинг программы на макроязыке Mathcad, позво-

ляющей рассчитать силу избыточного гидростатического давления на пло-

скую загубленную трапецеидальную стенку и место положение центра

давления.

Листинг 2.1.

Определение силы избыточного гидростатического давления и местоположения

центра давления на плоскую трапецеидальную стенку. Верхнее основание этой

площадки В погружено под свободную поверхность на глубину h

, а нижнее осно-

вание b - на глубину Н. Площадка составляет с горизонтом угол α.

Дано

B:=3 b:=2 H:=5 h0:=1 γ:=9810 α:=π/2

Результат:

Решение

γ Hh0−()⋅

6 sin α

()

⋅

HB 2b⋅+()⋅ h0 2 B⋅ b+()⋅+[

]

⋅:=

Hh0−()HB3b⋅+()⋅ h0 3 B⋅ 5b⋅+()⋅+[]⋅ 6h0

⋅ Bb+()+

2h0b 2B⋅+()⋅ HB 2b⋅+()⋅+[]⋅ sin α

()

⋅

P H

Zd 4.703= m

Рис. 2.6.

2.7. Эпюры давления

В некоторых случаях для наглядности можно пользоваться диаграм-

мами распределения давления по смоченной поверхности. Такие диаграм-

мы называются эпюрами давления.

Определение 22.

Эпюра

гидростатического

давления

график, построенный для плоской пря-

моугольной фигуры «стенки» - верти-

кальной или наклонной – подверженный

гидростатическому давлению, выра-

жающий распределение гидростатиче-

ского давления вдоль вертикального се-

чения стенки

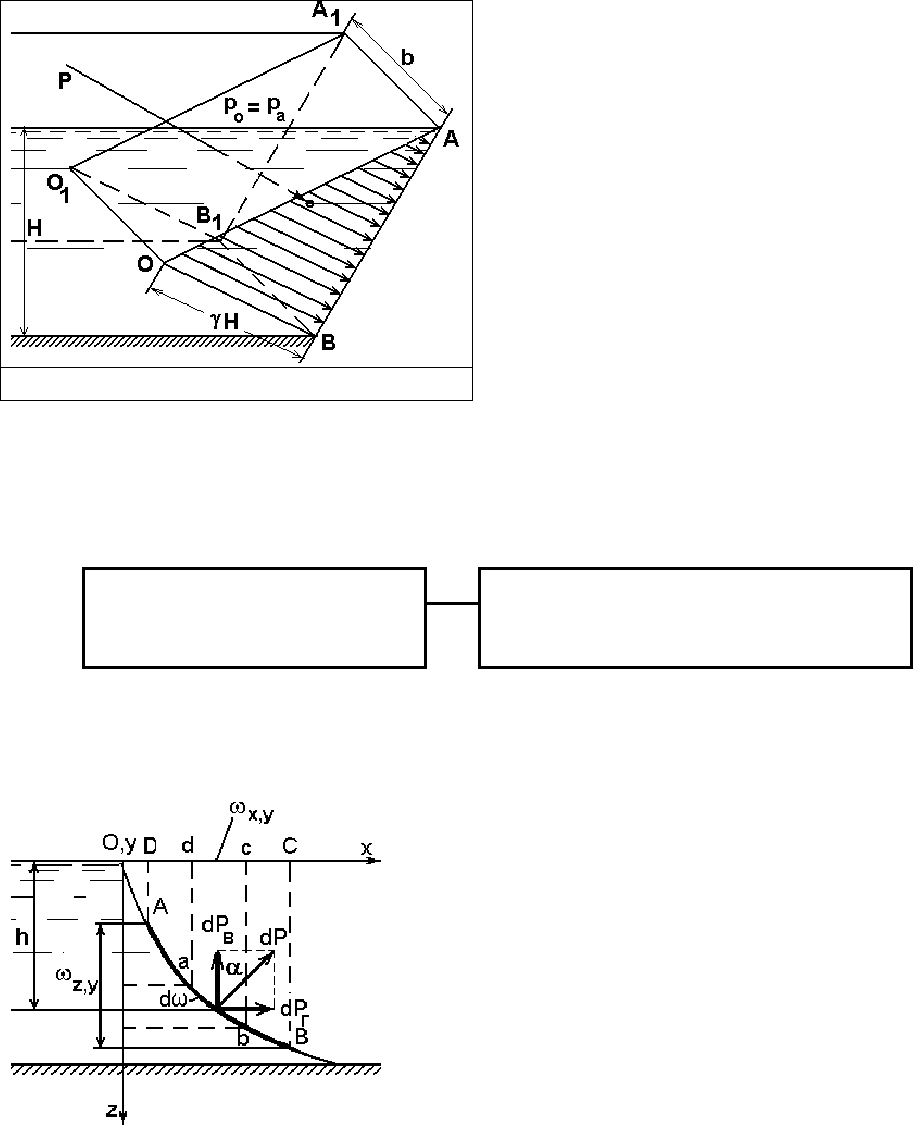
Рассмотрим прямоугольную стенку шириной b (Рис. 2.7)в аксоно-

метрии. Избыточное давление р в точке А равно нулю, а в точке В равно

γH. Так как в каждой точке смоченной поверхности стенки давление нор-

мально к ней, то отрезок, равный γH, откладываем на перпендикуляре, вос-

становленным к стенке в точке

В. Конец отрезка (точку О) соединяем с

()

43 ;

312 32

43 4

дд

Prhr

rhrh

γπ

ππ

(2.33)

точкой А прямой. Треугольник

АВО будет плоской эпюрой избы-

точного давления. Построенная

эпюра показывает распределение

этого давления по высоте стенки,

проведенной из любой точки ее

основания. Поэтому распределение

давления по всей стенки можно

представить пространственной

эпюров виде треугольной призмы

АВОО

. Каждая ордината этой

призмы представляет в некотором

масштабе избыточной давление в

соответствующей точке стенки, а весь объем призмы равен суммарному

избыточному давлению жидкости на стенку.

Определение 23.

Сила гидростатического

давления (абсолютного

или избыточного)

равна площади эпюры гидроста-

тического давления умноженной

на ширину перемычки

2.8. Сила гидростатического давления, действующая на

цилиндрические поверхности

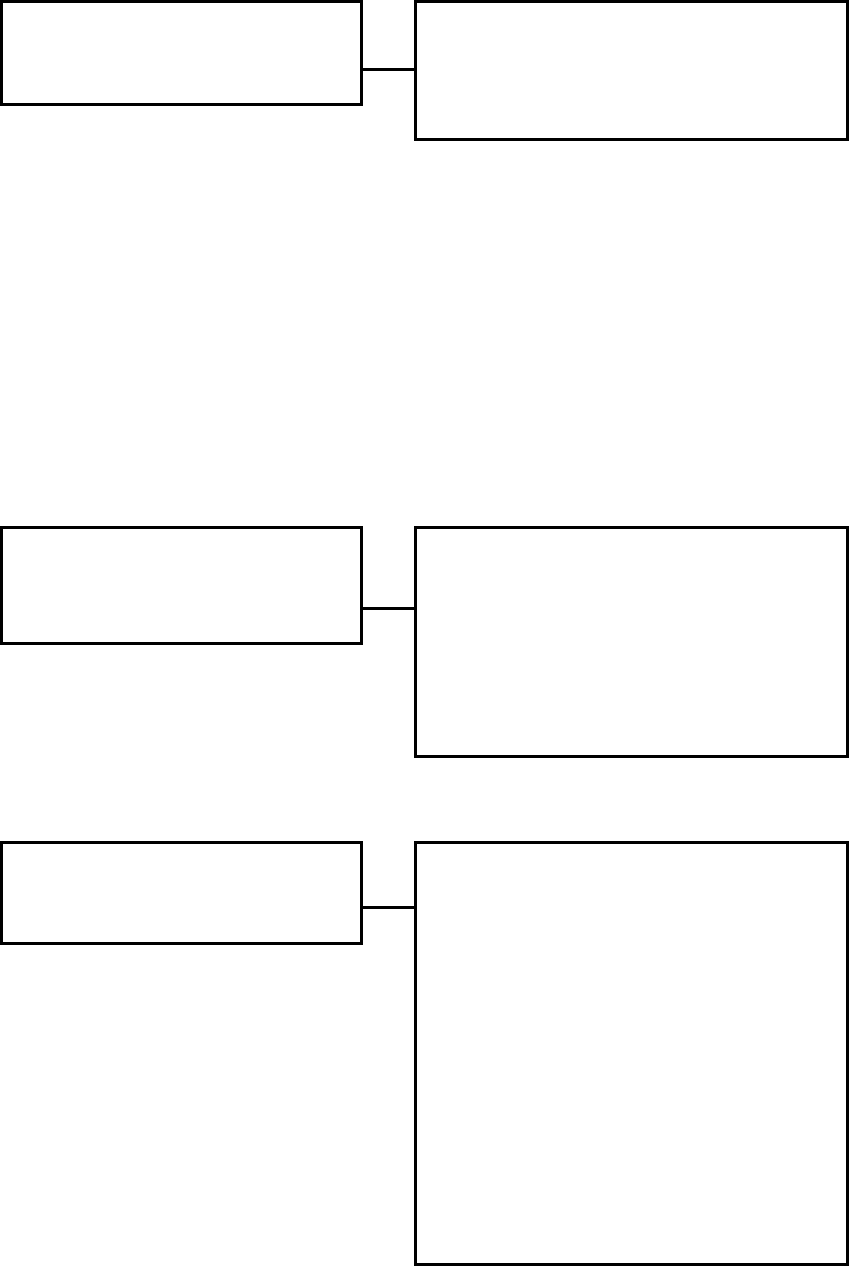
В практике приходиться определять

силу гидростатического давления не

только на плоские, но и на криволиней-

ные поверхности любого вида. Ниже рас-

смотрим только цилиндрические поверх-

ности с горизонтальной образующей.

Выделим на некоторой цилиндри-

ческой поверхности АВ элементарную

площадку dω с центром тяжести, погру-

женным на глубину h под свободную по-

верхность жидкости. Если давление на

поверхности равно р

, то полное гидро-

статическое давление в центре тяжести площадки dω составит:

+ .

Тогда элементарная сила полного гидростатического давления на

площадку dω будет равна:

и направлена по нормали к ней, проведенной через ее центр тяжести.

Рис. 2.7

Рис. 2.8

(

)

dP p h d

(2.34)

Разложив элементарную силу полного гидростатического давления

на вертикальную и горизонтальную составляющие, обозначив угол откло-

нения линии ее действия от вертикали через α:

Произведения cosαdω и sinαdω соответственно равны площадям

проекций элементарной площадки dω на горизонтальную xOy и вертикаль-

ную yOz плоскости, т.е.

Используя эти зависимости можно переписать

систему (2.35) в сле-

дующем виде

Если всю поверхность АВ разбить на ряд элементарных площадок

dω и для каждой из них определить значения dP

и dP

, то вертикальную и

горизонтальную составляющие силы полного гидростатического давления

жидкости на цилиндрическую поверхность АВ можно найти путем интег-

рирования

Первые интегралы в данной системе уравнений равны соответствен-

но площадям проекций цилиндрической поверхности АВ на горизонталь-

ную xOy и вертикальную yOz плоскости, т.е. ω

x,y

и ω

z,y

Проведя вертикальные образующие через различные точки перимет-

ра элементарной площадки dω до координатной плоскости xOy, получим

некоторый элементарный объем abcd, равный hdω

x,y

, т.е. как раз объем, за-

писанный под вторым интегралом в уравнении (2.38). Этот элементарный

объем abcd называется объемом тела давления. Уравнение это перепишет-

ся теперь в следующем виде

т.е.

(

)

(

)

()

cos cos

sin cos

dP dP p h d вертикальная составляющая

dP dP p h d горизонтальнаясоставляющая

αγαω

⎫

==+

⎪

⎬

==+

⎪

⎭

(2.35)

cos ;

sin .

αω ω

⎫

⎪

⎬

⎪

⎭

(2.36)

(

)

()

;

в xy

г zy

dP p h d

γω

⎫

⎪

⎬

⎪

⎭

(2.37)

0, ,

;

xy xy

zy zy

в xy xy

г zy zy

Pp d hd

dP p d hd

ωω

ωγ ω

⎫

⎪

⎬

⎪

⎭

∫∫

(2.38)

(

)

в xy

Pp объем ABCD

(2.39)

Определение 24.

Вертикальная составляю-

щая силы полного гидро-

статического давления

равна сумме силы внешнего дав-

ления на горизонтальную проек-

цию цилиндрической поверхно-

сти и весу объема тела давления.

Второй интеграл уравнения (2.38) равен статическому моменту пло-

щади проекции цилиндрической поверхности АВ на вертикальную плос-

кость zOy относительно оси Oy:

где h

– глубина погружения центра тяжести площади ω

z,y

Тогда

Следовательно

Определение 25.

Горизонтальная состав-

ляющая силы полного гид-

ростатического давления

равна силе абсолютного

гидростатического давления, под

воздействием которого находить-

ся вертикальная плоская стенка,

равная по площади вертикальной

проекции цилиндрической по-

верхности

Определение 26.

Поперечное сечение тела

давления (отрицательного

или положительного)

представляет собой фигуру, за-

ключенную между вертикалями,

проведенными по касательной к

криволинейной поверхности и

горизонтом жидкости (или его

продолжением).

Если рассматриваемая цилиндри-

ческая поверхность со стороны

тела давления не смачивается

жидкостью, то имеем отрица-

тельное тело давления, в против-

ном случае – положительное тело

давления.

yyczy

hd S h

∫

(2.40)

(

)

г czy

Pp h

(2.41)

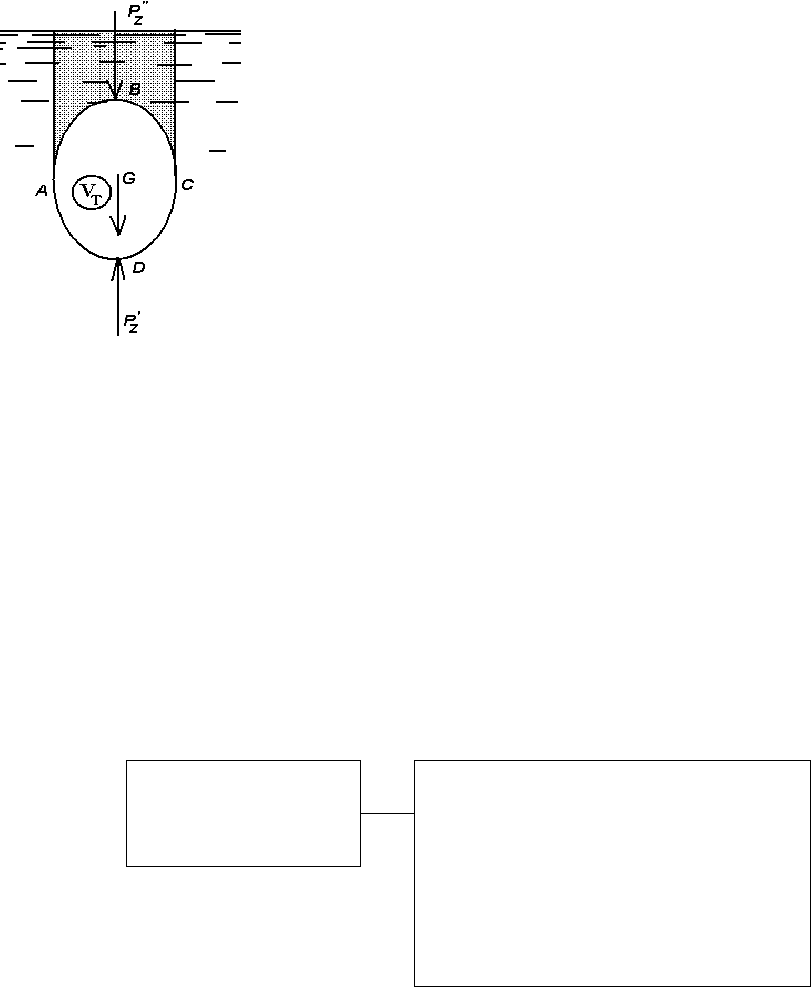
2.9. Закон Архимеда. Плавание тел

Пусть тело ABCD погружено в жидкость, и нужно определить вели-

чину суммарного давления жидкости на это тело (Рис. 2.9).

Горизонтальная составляющая давления жид-

кости на криволинейную поверхность тела будет

равна

PzF

, где F

– проекция на вертикальную

плоскость, а z

– глубина погружения центра тяже-

сти вертикальной проекции тела.

Так как проекция поверхности как левой, так и

правой половины тела на вертикальную поверх-

ность, перпендикулярную плоскости чертежа будет

одна та же, то величины горизонтальных состав-

ляющих полного давления на тело слева и справа

будут равны и противоположны по направлению,

т.е.

взаимно уничтожаются. Также будут равны и

взаимно противоположны горизонтальные силы давления на поверхность

тела в перпендикулярной чертежу плоскости.

Вертикальная составляющая полного давления жидкости на поверх-

ность тела будет состоять из сил

zADC

= и

zABC

Равнодействующая направленных в разные стороны сил вертикаль-

ного давления будет равна их разности

(

)

'''

z z z ADC ABC T

PPP V V V

=−= − =

Разность объемов тел давления дает объем самого тела V

Определение 27.

Закон Архимеда

Всякое погружаемое в жид-

кость тело будет испытывать

со стороны тела давление , на-

правленное снизу вверх и рав-

ное весу жидкости в объеме

тела (или его погруженной

части)

На законе Архимеда основана теория плавания тел. Всякое погру-

женное в жидкость тело с объемным весом γ

и находиться под действием

двух сил: силы веса тела G=γ

V и равнодействующей давления жидкости

=γV.

Здесь для однородного тела могут встретиться три случая:

;

> так как

(

)

GP V

−

=−, то тело потонет, сумма сил G и

Pz дает равнодействующую, направленную вниз;

Рис. 2.9