CIMA - C3 Fundamentals Of Business Mathematics
Подождите немного. Документ загружается.


50 1b: Formulae and equations ⏐ Part A Basic mathematics
2.3 Solving inequalities
We can solve inequalities in the same way we can solve equations. For example, the inequality 7x – 2 > 0 can be
solved by getting x on its own, but the answer will be a range of values rather than a specific number.
7x – 2 > 0
7x > 2 (add 2 to both sides)
x >
2
7
(divide both sides by 7)
2.4 Rules for manipulating inequalities
(i) Adding or subtracting the same quantity from both sides of an inequality leaves the inequality
symbol unchanged
(ii) Multiplying or dividing both sides by a positive number leaves the inequality symbol unchanged
(iii) Multiplying or dividing both sides by a negative number reverses the inequality so < changes to >
2.5 Example: Solving inequalities
Find the range of values of x satisfying x – 5 < 2x + 7
x – 5 < 2x + 7
x < 2x + 12 (add 5 to both sides)
-x < 12 (subtract 2x from both sides)
x > -12 (multiply both sides by -1 and so reverse the inequality)
Question
Solving inequalities
Solve the following inequalities
(a) 2x > 11
(b) x + 3 > 15
(c) -3x < 7
(d) 7x + 11 > 2x + 5
(e) 2(x + 3) < x + 1
Answe
r
(a) 2x > 11
x >
11
2
(divide both sides by 2)
x > 5.5
(b) x + 3 > 15
x > 12 (subtract 3 from both sides)
(c) -3x < 7
- x <
7
3
(divide both sides by 3)
x > -
7
3
(multiply both sides by -1 and so reverse the inequality)

Part A Basic mathematics ⏐ 1b: Formulae and equations 51
(d) 7x + 11 > 2x + 5
5x > -6 (subtract 2x and 11 from both sides)
x > -
6
5
(divide both sides by 5)
(e) 2(x + 3) < x + 1
2x + 6 < x + 1 (multiply out the brackets)
x < -5 (subtract x and 6 from both sides)
3 Linear equations
A linear equation has the general form y = a + bx
where y is the dependent variable, depending for its value on the value of x
x is the independent variable whose value helps to determine the corresponding value of y
a is a constant, that is, a fixed amount
b is also a constant, being the coefficient of x (that is, the number by which the value of x should be
multiplied to derive the value of y)
3.1 Example: Establishing basic linear equations
(a) Let us establish some basic linear equations. Suppose that it takes Joe Bloggs 15 minutes to walk one mile.
How long does it take Joe to walk two miles? Obviously it takes him 30 minutes. How did you calculate the
time? You probably thought that if the distance is doubled then the time must be doubled. How do you
explain (in words) the relationships between the distance walked and the time taken? One explanation
would be that every mile walked takes 15 minutes. Now let us try to explain the relationship with an
equation.
(b) First you must decide which is the
dependent variable and which is the independent variable. In other
words, does the time taken depend on the number of miles walked or does the number of miles walked
depend on the time it takes to walk a mile? Obviously the time depends on the distance. We can therefore
let y be the dependent variable (time taken in minutes) and x be the independent variable (distance walked
in miles).
(c) We now need to determine the constants a and b. There is no fixed amount so a = 0. To ascertain b, we
need to establish the number of times by which the value of x should be multiplied to derive the value of y.
Obviously y = 15x where y is in minutes. If y were in hours then y = x/4.
3.2 Example: Deriving a linear equation
A salesman's weekly wage is made up of a basic weekly wage of $100 and commission of $5 for every item he
sells. Derive an equation which describes this scenario.
Solution
x = number of items sold and y = weekly wage
a = $100 (fixed weekly wage paid however many items he sells) and b = $5 (variable element of wage, depends
on how many items he sells)
∴ y = 5x + 100
FA
S
T F
O
RWAR
D

52 1b: Formulae and equations ⏐ Part A Basic mathematics
Note that the letters used in an equation do not have to be x and y. It may be sensible to use other letters, for
example we could use p and q if we are describing the relationship between the price of an item and the quantity
demanded.
4 Linear equations and graphs
The graph of a linear equation is a straight line. The intercept of the line on the y axis is a in:
y = a + bx
where a = the intercept of the line on the y axis
and b = the slope of the line
One of the clearest ways of presenting the relationship between two variables is by plotting a linear equation as a
straight line on a graph.
4.1 The rules for drawing graphs
A graph has a horizontal axis, the x axis and a vertical axis, the y axis. The x axis is used to represent the
independent variable and the y axis is used to represent the dependent variable. If calendar time is one variable,
it is always treated as the independent variable. When time is represented on the x axis of a graph, we have the
graph of a time series.
(a) If the data to be plotted are derived from calculations, rather than given in the question, make sure
that there is a neat table in your workings.
(b) The scales on each axis should be selected so as to use as much of the graph paper as possible. Do
not cramp a graph into one corner.
(c) In some cases it is best not to start a scale at zero so as to avoid having a large area of wasted
paper. This is perfectly acceptable as long as the scale adopted is clearly shown on the axis. One
way of avoiding confusion is to break the axis concerned, as shown below.
(d) The scales on the x axis and the y axis should be marked. For example, if the y axis relates to
amounts of money, the axis should be marked at every $1, or $100 or $1,000 interval or at whatever
other interval is appropriate. The axes must be marked with values to give the reader an idea of how
big the values on the graph are.
(e) A graph should not be overcrowded with too many lines. Graphs should always give a clear, neat
impression.
FA
S
T F
O
RWAR
D
Part A Basic mathematics ⏐ 1b: Formulae and equations 53
(f) A graph must always be given a title, and where appropriate, a reference should be made to the
source of data.
4.2 Example: Drawing graphs
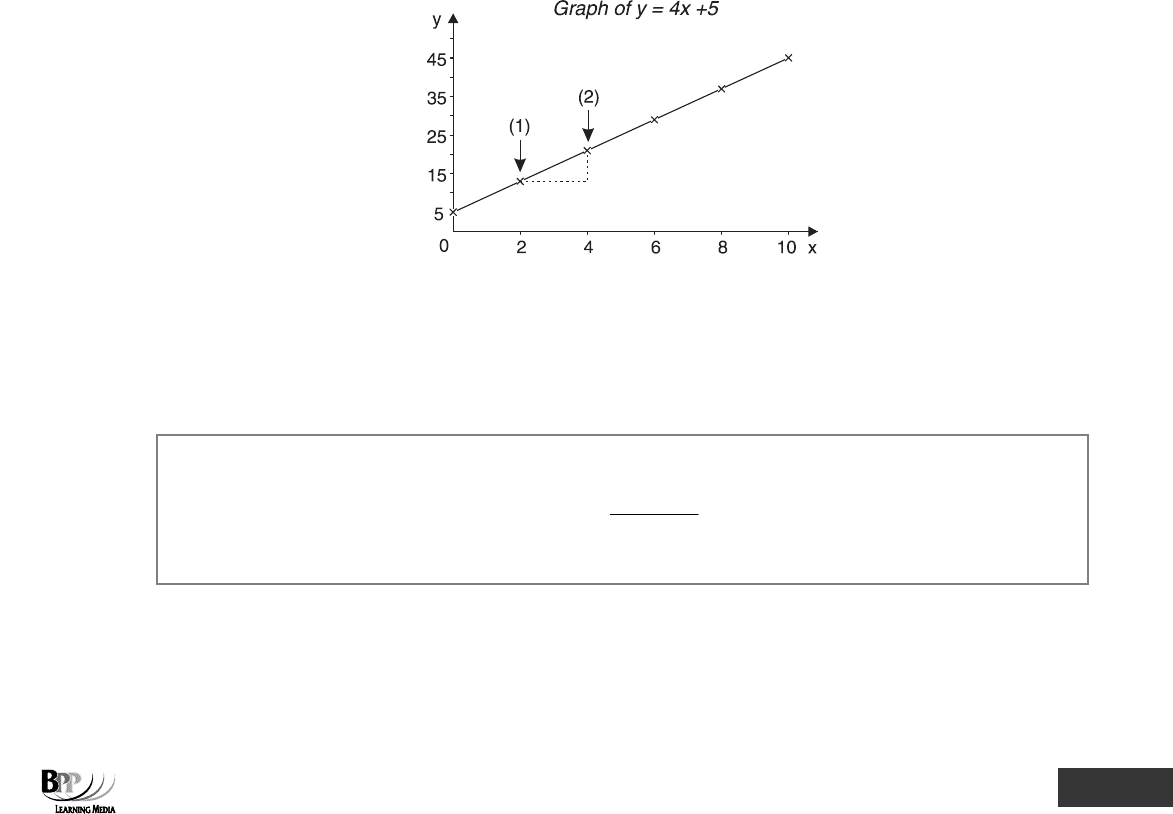
Plot the graph for y = 4x + 5.
Consider the range of values from x = 0 to x = 10.
Solution
The first step is to draw up a table for the equation. Although the problem mentions x = 0 to x = 10, it is not
necessary to calculate values of y for x = 1, 2, 3 etc. A graph of a linear equation can actually be drawn from just
two (x, y) values but it is always best to calculate a number of values in case you make an arithmetical error. We
have calculated five values, but three would be enough in your assessment.
x y
0 5
2 13
4 21
6 29
8 37
10 45
4.3 The intercept and the gradient
The graph of a linear equation is determined by two things.
• The gradient (or slope) of the straight line
• The point at which the straight line crosses the y axis
• The intercept is the point at which a straight line crosses the y-axis.
• The gradient of the graph of a linear equation is
change in y
change in x
= (y
2
– y
1
)/(x
2
– x
1
) where (x
1
, y
1
) and
(x
2
, y
2
) are two points on the straight line.
4.3.1 The intercept
The intercept of y = 4x + 5 is where y = 5. It is no coincidence that the intercept is the same as the constant
represented by a in the general form of the equation y = a + bx. a is the value y takes when x = 0, in other words a
constant.
Key term
54 1b: Formulae and equations ⏐ Part A Basic mathematics
4.3.2 The gradient
If we take two points on the line (see graph in 4.2):
(1) x = 2, y = 13
(2) x = 4, y = 21
The gradient of y = 4x + 5 =
change in y
change in x
=
(
)
()
2
8
24
1321
=
−
−
= 4
Notice that the gradient is also given by the number multiplied by x in the equation (b in the general form of the
equation).
Question
Gradient
If y = 10 – x, the gradient =
Answe
r
The gradient =
–1
If y = 10 – x, then a = 10 and b = –1 (–1
× x = –x).
Therefore gradient = –1
4.3.3 Positive and negative gradients
Note that the gradient of y = 4x + 5 is positive whereas the gradient of y = 10 – x is negative.
• A positive gradient slopes upwards from left to right
• A negative gradient slopes downwards from left to right
• The greater the value of the gradient, the steeper the slope
Question
Intercept and gradient
What is the intercept and gradient of the graph of 4y = 16x
− 12?
Intercept Gradient
A –3 +4
B –4 +3
C +3 –4
D +4 –3
Answe
r
4y = 16x
− 12
Equation must be in the form y = a + bx
y = 4x – 3 (divide both sides by 4)
y = –3 + 4x (rearrange the RHS)
Part A Basic mathematics ⏐ 1b: Formulae and equations 55
Intercept = a = −3
Gradient = b = 4
Therefore the correct answer is A.
If you selected option D, you have obviously confused the intercept and the gradient. Remember that with an
equation in the form y = a + bx, a = intercept (ie where the line of the graph crosses the y axis) and b = the slope or
gradient of the line.
Question
Linear graphs
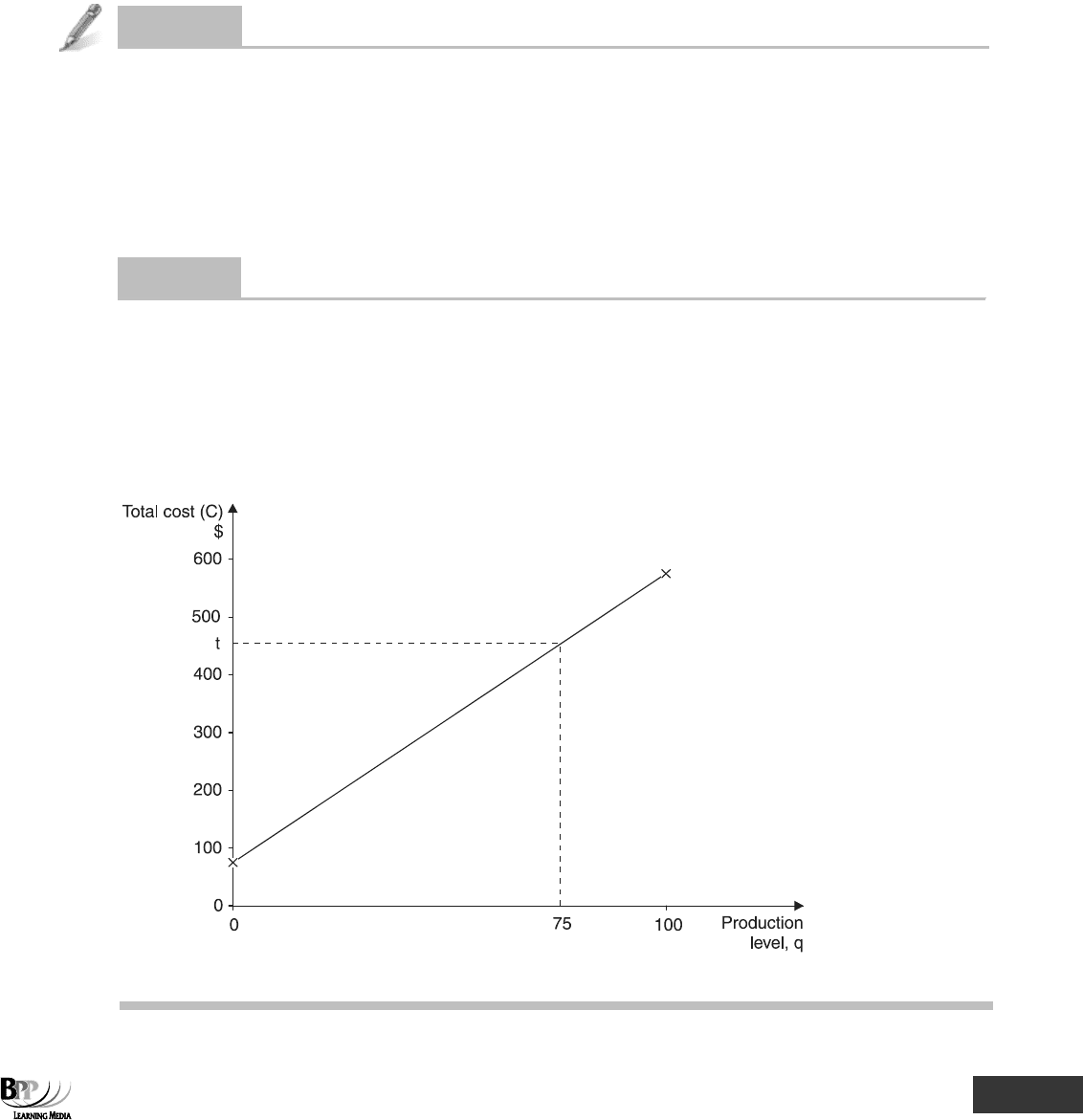
A company manufactures a product. The total fixed costs are $75 and the variable cost per unit is $5.
Required
(a) Find an expression for total costs (c) in terms of q, the quantity produced.
(b) Use your answer to (a) to determine the total costs if 100 units are produced.
(c) Prepare a graph of the expression for total costs.
(d) Use your graph to determine the total cost if 75 units are produced.
Answe
r
(a) Let C = total costs
C = total variable costs + total fixed costs
C = 5q + 75
(b) If q = 100, C = (5
× 100) + 75 = $575
(c) If q = 0, C = $75
If q = 100, C = $575
(d) From graph above, if q = 75, C = $450
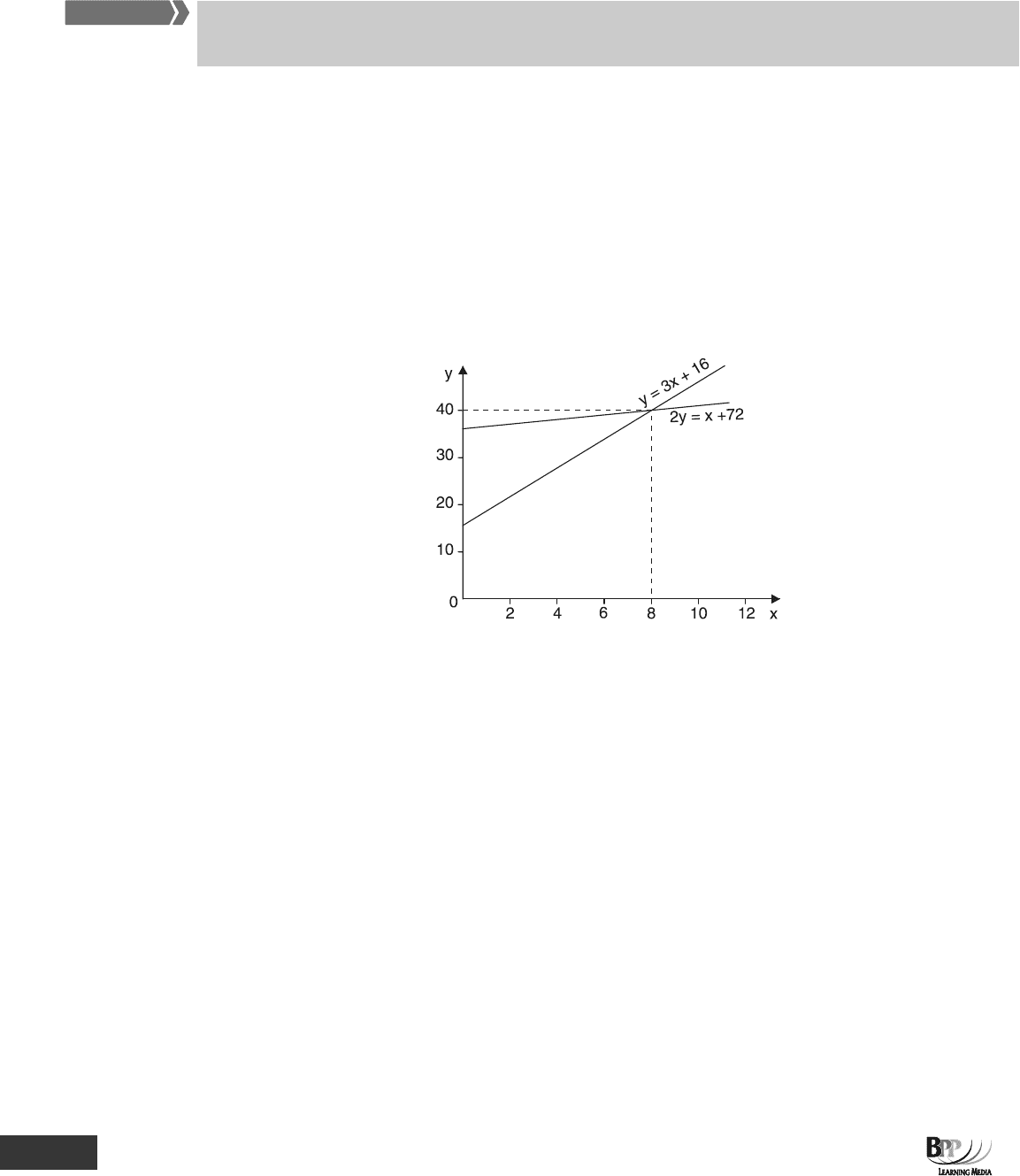
56 1b: Formulae and equations ⏐ Part A Basic mathematics
5 Simultaneous equations
Simultaneous equations are two or more equations which are satisfied by the same variable values. They can be
solved graphically or algebraically.
5.1 Example: Simultaneous equations
The following two linear equations both involve the unknown values x and y. There are as many equations as there
are unknowns and so we can find the values of x and y.
y = 3x + 16
2y = x + 72
5.1.1 Solution: Graphical approach
One way of finding a solution is by a graph. If both equations are satisfied together, the values of x and y must be
those where the straight line graphs of the two equations
intersect.
Since both equations are satisfied, the values of x and y must lie on both the lines. Since this happens only once, at
the intersection of the lines, the value of x must be 8, and of y 40.
5.1.2 Solution: Algebraic approach
A more common method of solving simultaneous equations is by algebra.
(a) Returning to the original equations, we have:
y = 3x + 16 (1)
2y = x + 72 (2)
(b) Rearranging these, we have:
y – 3x = 16 (3)
2y – x = 72 (4)
(c) If we now multiply equation (4) by 3, so that the coefficient for x becomes the same as in equation
(3) we get:
6y – 3x = 216 (5)
y – 3x = 16 (3)
FA
S
T F
O
RWAR
D

Part A Basic mathematics ⏐ 1b: Formulae and equations 57
(d) Subtracting (3) from (5) we get:
5y = 200
y = 40
(e) Substituting 40 for y in any equation, we can derive a value for x. Thus substituting in equation (4)
we get:
2(40) – x = 72
80 – 72 = x
8 = x
(f) The solution is y = 40, x = 8.
Question
Simultaneous equations
Solve the following simultaneous equations using algebra.
5x + 2y = 34
x + 3y = 25
Answe
r
5x + 2y = 34 (1)
x + 3y = 25 (2)
Multiply (2)
× 5:
5x + 15y = 125 (3)
Subtract (1) from (3):
13y = 91
y = 7
Substitute into (2):
x + 21 = 25
x = 25 – 21
x = 4
The solution is x = 4, y = 7.
An assessment question might ask you to find the co-ordinates of the intersection point of two lines and give you
two equations. You need to calculate the values of x and y using the simultaneous equation technique.
6 Non-linear equations
So far we have looked at equations in which the highest power of the unknown variable(s) is one (that is, the
equation contains x, y but not x
2
, y
3
and so on). We are now going to turn our attention to non-linear equations.
In non-linear equations, one variable varies with the n
th
power of another, where n>1. The graph of a non-linear
equation is not a straight line.
FA
S
T F
O
RWAR
D
Assessment
focus point
58 1b: Formulae and equations ⏐ Part A Basic mathematics
6.1 Examples: Non-linear equations
(a) y = x
2
; y = 3x
3
+ 2; 2y = 5x
4
– 6; y = –x
12
+ 3
(b) It is common for a non-linear equation to include a number of terms, all to different powers. Here are some
examples.
y = x
2
+ 6x + 10 y = –12x
9
+ 3x
6
+6x
3
+ 3x
2
– 1
2y = 3x
3
– 4x
2
–8x + 10 3y = 22x
8
+ 7x
7
+ 3x
4
– 12
6.2 Graphing non-linear equations
The graph of a linear equation, as we saw earlier, is a straight line. The graph of a non-linear equation, on the
other hand,
is not a straight line. Let us consider an example.
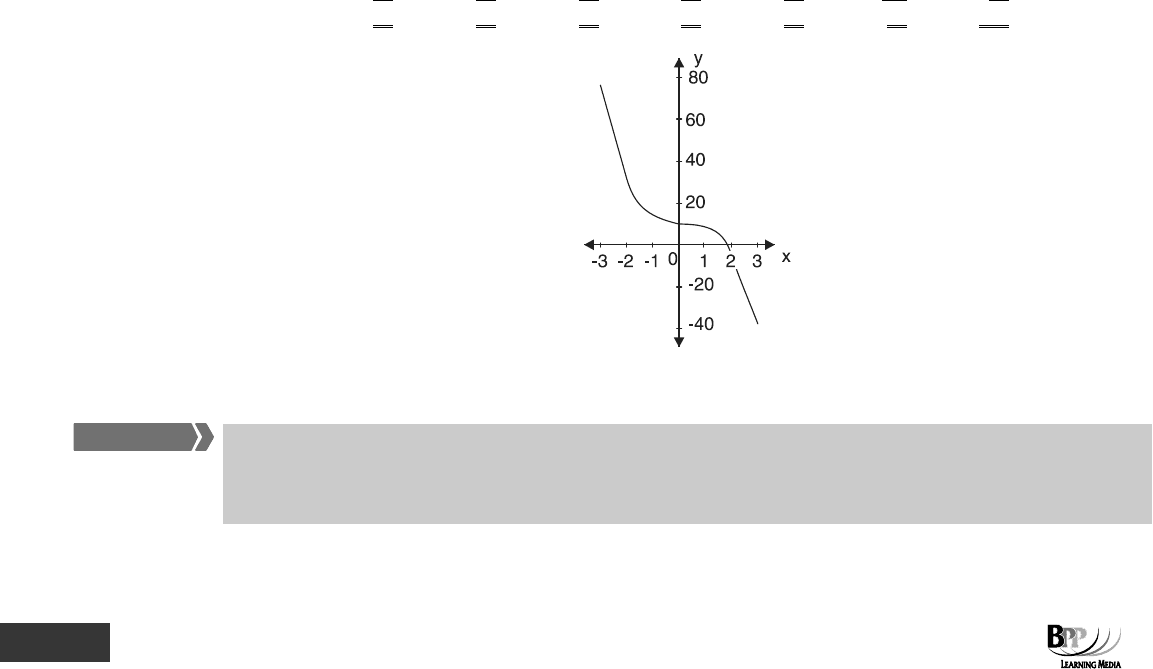
6.2.1 Example: Graphing non-linear equations
Graph the equation 10x2xx2y
23
+−+−= .
Solution
The graph of this equation can be plotted in the same way as the graph of a linear equation is plotted. Take a
selection of values of x, calculate the corresponding values of y, plot the pairs of values and join the points
together. The joining must be done using as smooth a curve as possible.
x
–3
–2
–1
0
1
2
3
–2x
6
4
2
0
–2
–4
–6
x
2
9
4
1
0
1
4
9
–2x
3
54
16
2
0
–2
–16
–54
10
10
10
10
10
10
10
10
y
79
34
15
10
7
–6
–41
6.3 Quadratic equations
Quadratic equations are a type of non-linear equation in which one variable varies with the square (or second
power) of the other variable. They can be expressed in the form
y = ax
2
+ bx + c.
A quadratic equation may include both a term involving the square and also a term involving the first power of a
variable. Here are some examples.
FA
S
T F
O
RWAR
D
Part A Basic mathematics ⏐ 1b: Formulae and equations 59
y = x
2
y = x
2
+ 6x + 10 2y = 3x
2
– 4x – 8 y = 5x
2
+ 7
In the equation y = 3x
2
+ 2x – 6, a = 3, b = 2, c = –6.
6.3.1 Graphing a quadratic equation
The graph of a quadratic equation can be plotted using the same method as that illustrated in Paragraph 6.2.1.
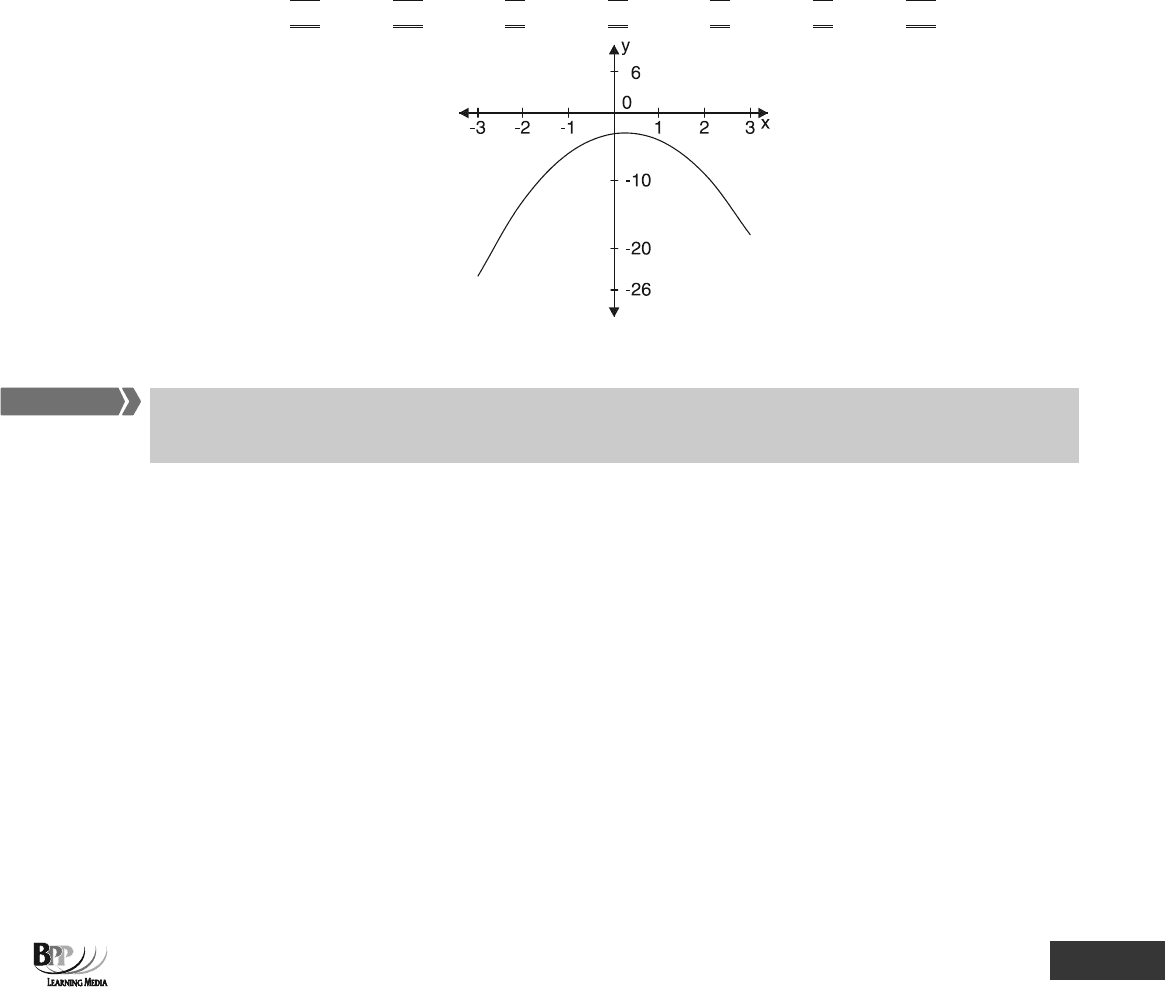
6.3.2 Example: Graphing a quadratic equation
Graph the equation 3xx2y
2
−+−=
Solution
x
–3
–2
–1
0
1
2
3
–2x
2
–18
–8
–2
0
–2
–8
–18
–3
–3
–3
–3
–3
–3
–3
–3
y
–24
–13
–6
–3
–4
–9
–18
6.3.3 Parabolas
The graphs of quadratic equations are parabolas, the sign of 'a' in the general form of the quadratic equation (y =
ax
2
+ bx + c) determining the way up the curve appears.
(a) The constant term 'c' determines the value of y at the point where the curve crosses the y axis (the
intercept). In the graph above, c = –3 and the curve crosses the y axis at y = –3.
(b) The sign of 'a' determines the way up the curve appears.
• If 'a' is positive, the curve is shaped like a ditch
• If 'a' is negative, as in Paragraph 6.3.2, the curve is shaped like a bell
A ditch-shaped curve is said to have a
minimum point whereas a bell-shaped curve is said to have a
maximum point.
(c) The graph enables us to find the values of x when y = 0 (if there are any). In other words the graph
allows us to solve the quadratic equation 0 = ax
2
+ bx + c. For the curve in Paragraph 6.3.2 we see
that there are no such values (that is, 0 = –2x
2
+ x – 3 cannot be solved).
FA
S
T F
O
RWAR
D
