CIMA - C3 Fundamentals Of Business Mathematics

60 1b: Formulae and equations ⏐ Part A Basic mathematics

6.4 Solving quadratic equations

The graphical method is not, in practice, the most efficient way to determine the solution of a quadratic equation.

Many quadratic equations have two values of x (called

'solutions for x' or 'roots of the equation') which satisfy the

equation for any particular value of y.

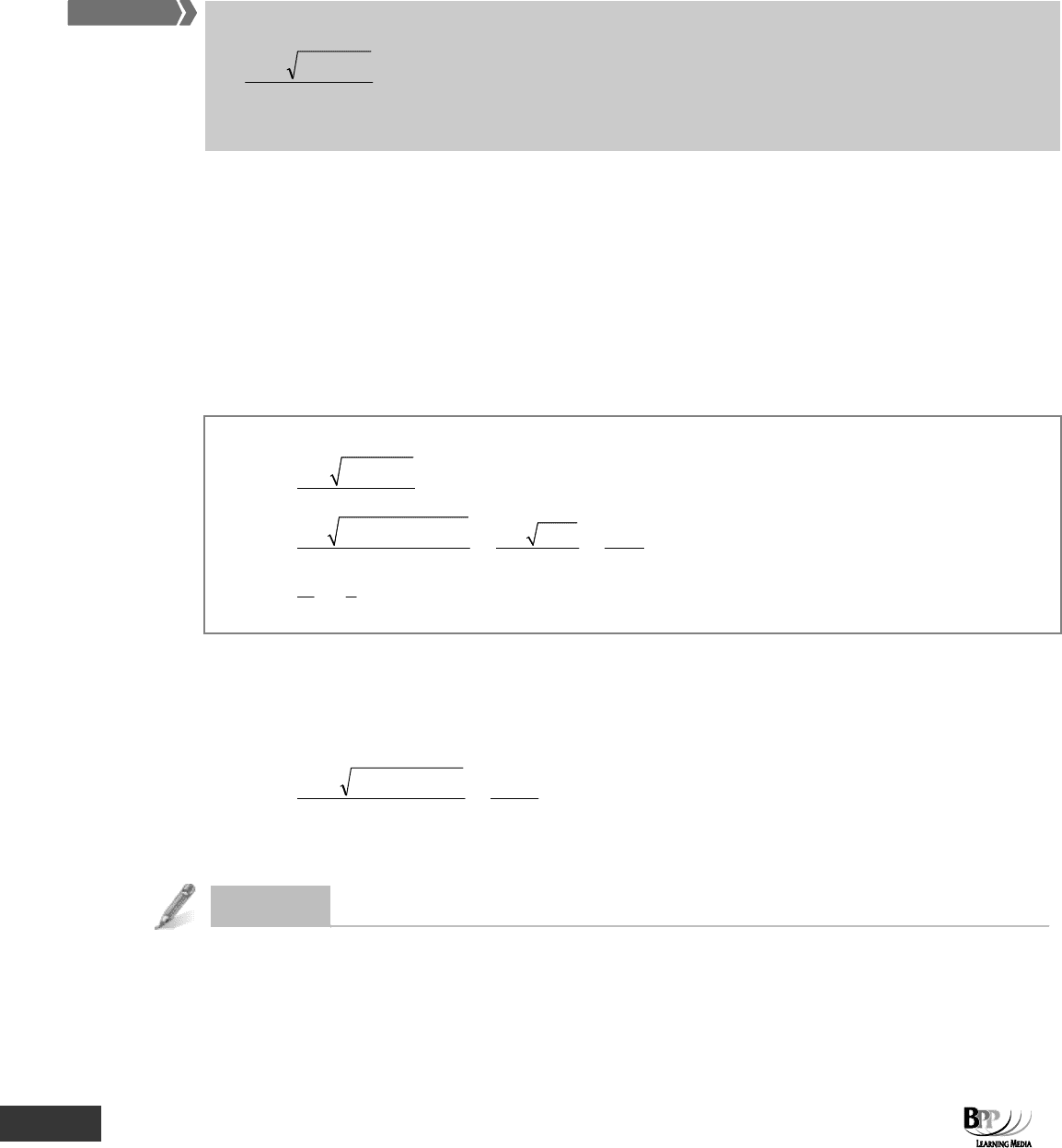
Quadratic equations can be solved by the formula:

x =

a2

)ac4b(b

2

−±−

when ax

2

+ bx + c = 0

You will be given this formula in your exam.

6.4.1 Example: Quadratic equations

Solve

.02xx

2

=−+

Solution

For the equation x

2

+ x – 2 = 0

a = 1

b = 1

c = –2

We can insert these values into the quadratic equation formula.

x =

2

-b (b 4ac)

2a

±−

x =

2

-1 (1 (4 1 ( 2)))

21

±−××−

×

=

-1 (1+8)

2

±

=

-1 3

2

±

∴ x =

-4

2

or

2

ie x = –2 or x = 1

6.5 Quadratic equations with a single value for x

Sometimes, b

2

– 4ac = 0, and so there is only one solution to the quadratic equation. Let us solve x

2

+ 2x + 1 = 0

using the formula above where a = 1, b = 2 and c = 1.

x =

2

))114(2(2

2

××−±−

=

2

02

±

−

= –1

This quadratic equation can only be solved by one value of x.

Question

Non-linear graphs

A company manufactures a product, the total cost function for the product being given by C = 25q – q

2

, where q is

the quantity produced and C is in $.

Required

(a) Calculate the total costs if 15 units are produced.

FA

S

T F

O

RWAR

D

Assessment

formula

Part A Basic mathematics ⏐ 1b: Formulae and equations 61

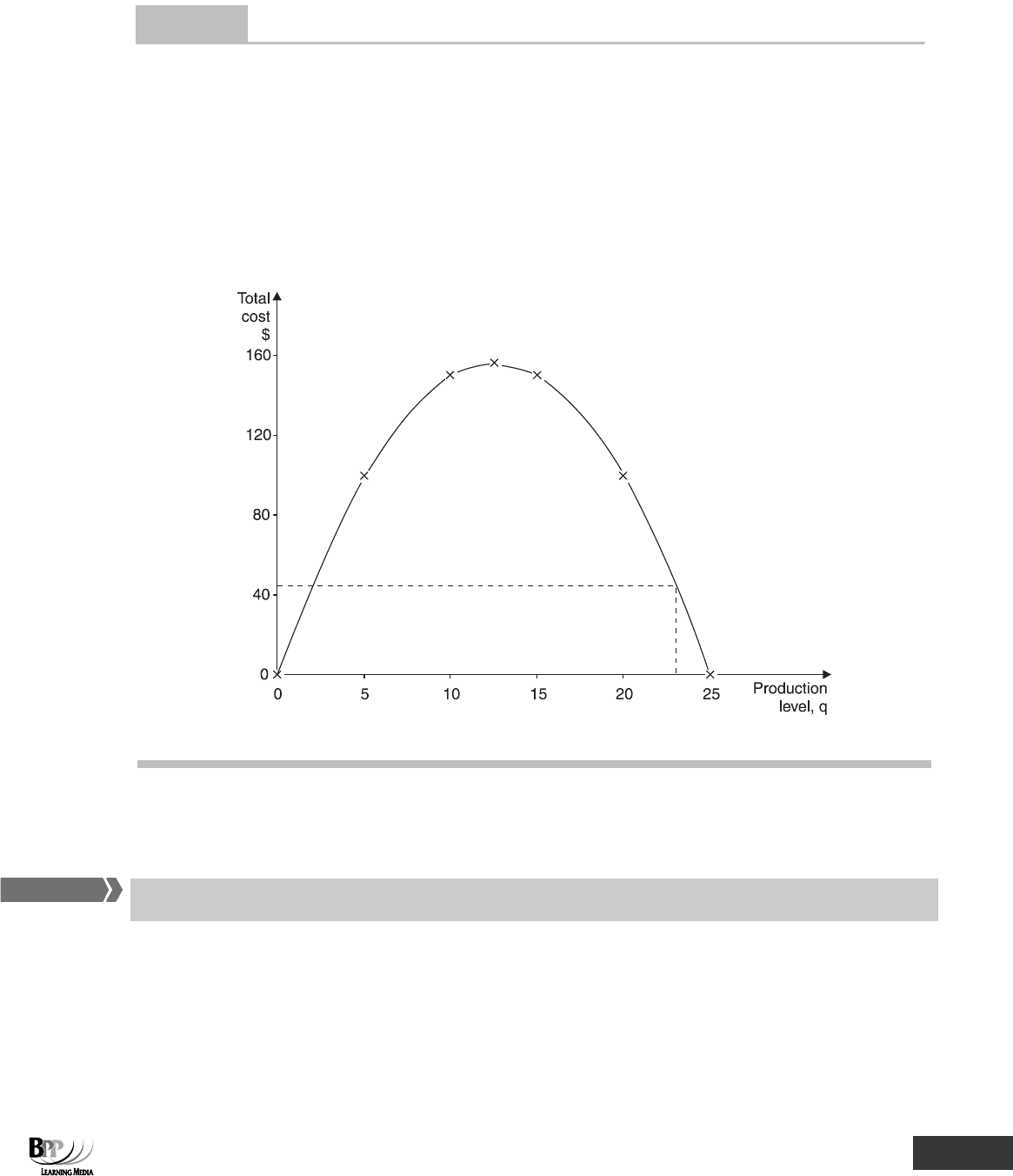
(b) Draw a graph of the total cost function and use it to calculate the total cost if 23 units are produced.

Answe

r

(a) C = 25q – q

2

If q = 15, C = (25 × 15) – 15

2

= 375 – 225 = $150

(b)

q C

0 0

5.0 100.00

10.0 150.00

12.5 156.25

15.0 150.00

20.0 100.00

25.0 0

From the graph, if 23 units are produced the total cost is approximately $45.

7 Using spreadsheets to produce graphs

Spreadsheets can be used to produce graphs of linear and quadratic equations.

Excel includes the facility to produce a range of charts and graphs which we will look at in more detail in Chapter 3.

7.1 The Chart Wizard

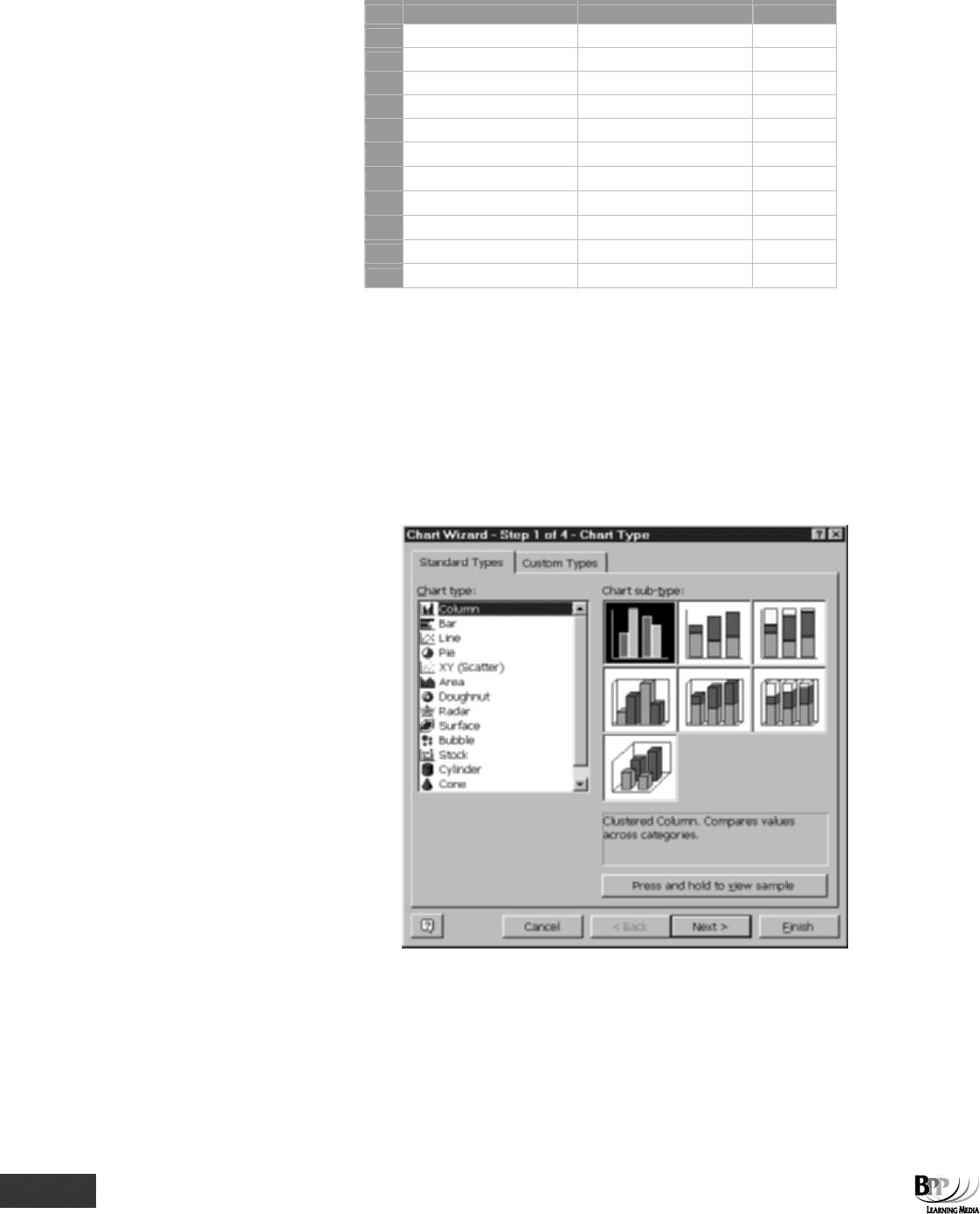
Charts and graphs may be generated simply by selecting the range of figures to be included, then using Excel's

Chart Wizard. A spreadsheet to produce a linear equation is shown below.

FA

S

T F

O

RWAR

D

62 1b: Formulae and equations ⏐ Part A Basic mathematics

A B C

1 Values for x y = 4x + 15

2 1 19

3 2 23

4 3 27

5 4 31

6 5 35

7 6 39

8 7 43

9 8 47

10 9 51

11

The following steps are taken from the Excel 2000 Chart Wizard. Other versions may differ slightly.

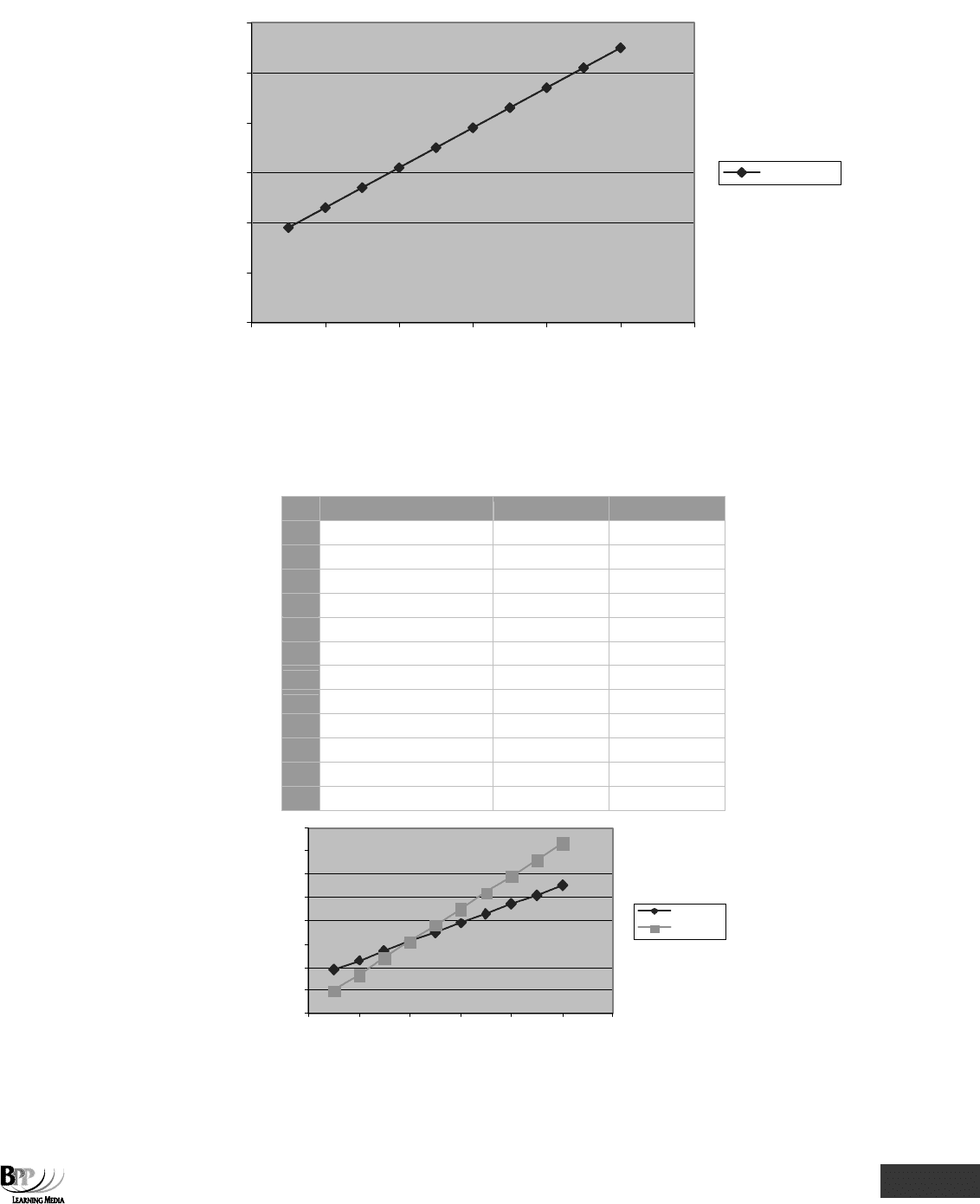
Step 3 Pick the type of chart you want. We will choose xy (scatter) connected by smoothed lines.

Step 4 Next, specify your chart title and axes labels.

Step 5 The final step is to choose whether you want the chart to appear on the same worksheet as the data

or on a separate sheet of its own.

Part A Basic mathematics ⏐ 1b: Formulae and equations 63

0

10

20

30

40

50

60

024681012

x values

y = 4x + 15

7.2 Simultaneous equations

We can also plot more than one equation on the same graph as can be seen below. Simply select all three columns

in the spreadsheet and then use the Chart Wizard as before.

A B C

1 Values for x y = 4x + 15 y = 7x + 3

2 1 19 10

3 2 23 17

4 3 27 24

5 4 31 31

6 5 35 38

7 6 39 45

8 7 43 52

9 8 47 59

10 9 51 66

11 10 55 73

12

0

10

20

30

40

50

60

70

80

024681012

Va lues for x

y = 4x + 15

y = 7 x + 3

y values

64 1b: Formulae and equations ⏐ Part A Basic mathematics

Chapter Roundup

• A formula enables us to calculate the value of one variable from the value(s) of one or more other variables.

• The general rule for solving equations is that you must always do the same thing to both sides of the equal sign

so the scales stay balanced.

• An inequality is a statement that shows the relationship between two (or more) expressions with one of the

following signs: >, ., <, -. We can solve inequalities in the same way that we can solve equations.

• A linear equation has the general form y = a + bx, where x is the independent variable and y the dependent

variable, and a and b are fixed amounts.

• The graph of a linear equation is a straight line, where y = a + bx. The intercept of the line on the y axis = a

and the gradient of the line = b.

• Simultaneous equations are two or more equations which are satisfied by the same variable values. They can be

solved graphically or algebraically.

• In non-linear equations, one variable varies with the n

th

power of another, where n > 1. The graph of a non-linear

equation is not a straight line.

• Quadratic equations are a type of non-linear equation in which one variable varies with the square (or second

power) of the other variable. They can be expressed in the form y = ax

2

+ bx + c.

• The graphs of quadratic equations are parabolas, the sign of 'a' in the general form of the quadratic equation (y =

ax

2

+ bx + c) determining the way up the curve appears.

• Quadratic equations can be solved by the formula

x =

2

b(b4ac)

2a

−± −

when ax

2

+ bx + c = 0

You will be given this formula in your exam.

• Spreadsheets can be used to produce graphs of linear and quadratic equations.

Part A Basic mathematics ⏐ 1b: Formulae and equations 65

Quick Quiz

1 A linear equation has the general form y = a + bx where

y independent variable

x constant (fixed amount)

b constant (coefficient of x)

a dependent variable

2 The horizontal axis on a graph is known as the y axis.

True

F

False

F

True False

3 (a) A positive gradient slopes upwards from right to left F F

(b) A negative gradient slopes downwards from left to right

F F

(c) The greater the value of the gradient, the steeper the slope

F F

4 Find the co-ordinates of the intersection point of the two lines y = 6x – 7 and y = –3x – 4

(x, y) = ( , )

5 Consider the equation

y = –4x

2

+3x – 2

(a) The graph of the equation is shaped like a ditch/bell

(b) The graph of the equation has a minimum/maximum point

(c) The point at which the curve crosses the y axis is ……………..

6 A formula used in financial mathematics is s = x (1+r)

n

Rearrange the formula to make r the subject.

Which of the following is correct?

A r =

x

s

+ 1

B r =

1

s

x

n −

C r =

1

x

s

n

−

D r =

n

x

1s −

7 If x = 300, r = 0.06 and n = 5, using the formula s = x (1 + r)

n

, what is the value of s? (to 2 decimal places)

8 If 1,200 = 4x

2

+ 20x, then the two values of x that satisfy this equation are:

?

66 1b: Formulae and equations ⏐ Part A Basic mathematics

9 Solve this inequality

3(x + 2) < x + 4

A x < – 2

B x < – 1

C x < 2

D x > – 1

Answers to Quick Quiz

1 y = dependent variable

x = independent variable

b = constant (coefficient of x)

a = constant (fixed amount)

2 False

3 (a) False

(b) True

(c) True

4 y = 6x – 7 (1)

y = –3x – 4 (2)

Multiply (2) by 2

2y = –6x – 8 (3)

Add (1) + (3)

3y = –15

y = –5

Substitute into (2)

–5 = –3x – 4

–1 = –3x

1 = 3x

x = 1/3

The co-ordinates of the intersection point are therefore (1/3, –5)

5 (a) bell

(b) maximum point

(c) –2

6 C

x

s

= (1 + r)

n

x

s

n = 1 + r

r =

1

x

s

n

−

Part A Basic mathematics ⏐ 1b: Formulae and equations 67

7

S = x (1 + r)

n

= 300 × (1 + 0.06)

5

= 401.47

8 1,200 = 4x

2

+ 20x

4x

2

+ 20x – 1,200 = 0

x =

a2

ac4bb

2

−+−

a = 4, b = 20, c = –1,200

x =

4 x 2

1,200) x 4 x (4 20 20

2

−−+−

=

8

19,600 20 +−

=

8

140 20 +−

= 15 or –20

9 B 3(x + 2) < x + 4

3x + 6 < x + 4

2x + 6 < 4

2x < –2

x < –1

Now try the questions below from the Exam Question Bank

Question numbers Pages

17–26 328-329

4

0

1.47

68 1b: Formulae and equations ⏐ Part A Basic mathematics

69

Part B

Summarising and

analysing data

CIMA - C3 Fundamentals Of Business Mathematics

Подождите немного. Документ загружается.