Численные методы турбулентных несжимаемых течений (Том 4 Часть 2)

Подождите немного. Документ загружается.

19.10 The 2nd Law of Thermodynamics 165

and noting that by the basic energy estimate (16.2)

νu

∇u

· ∇φ

dxdt → 0,

as ν tends to zero. We thus have for small ν that

E(u

, p

) ≈ ν|∇u|

, in Q, (19.8)

that is, E(u

, p

) is in fact approximately equal to the the intensity of the

viscous dissipation ν|∇u|

. In particular, we expect that E(u

, p

) > 0 for a

turbulent ﬂow with substantial turbulent dissipation.

So even if the existence of weak solutions to the Euler equations cannot

be proved, Duchon-Robert propose that it may be reasonable to require a

weak solution (u, p) of Euler to satisfy E(u, p) ≥ 0 in Q in a weak sense. The

rationale is that limits of solutions to the NS equations satisfy this condition,

as we just demonstrated, and therefore “physical solutions” should satisfy this

condition. The proof below that G2 satisﬁes a variant of the same condition

mimics the proof for NS equations just given. As indicated above, we have

strong reasons to believe that (stable) weak solutions to the Euler equations

do not exist, and thus that the notion of dissipative weak solution to Euler

may not be useful, but the notion of approximate dissipative weak solution is.

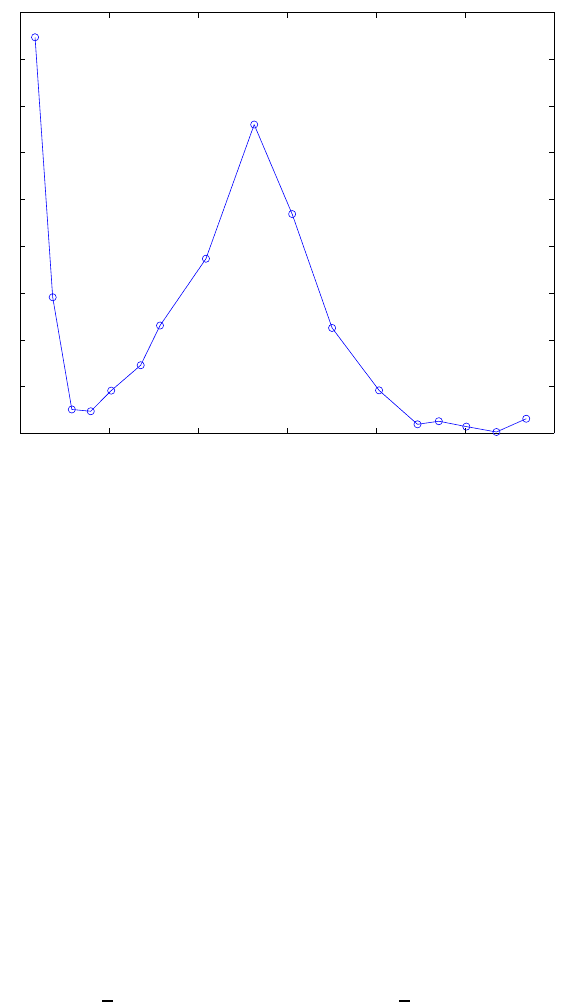
19.9 Finite Limit of Turbulent Dissipation

In this context, we recall Kolmogorov’s conjecture that the intensity of the

turbulent dissipation should have a ﬁnite limit diﬀerent from zero as ν tends

to zero. Studying Fig. 19.10 where we display the dissipation intensity in G2

as a function of the mesh size (log

of the number of mesh points), we see

that the intensity indeed seems to have a ﬁnite limit diﬀerent from zero. Thus

computation indicate that Kolmogorov was right. Of course, the alternative of

a zero limit does not seem plausible as that would correspond to the existence

of a (stable) smooth solution to the Euler equations, which we have seen is

impossible.

19.10 The 2nd Law of Thermodynamics

We can view D

T = E(u, p) ≥ 0 as an expression of the 2nd Law of thermo-

dynamics, reﬂecting that kinetic energy may be turned into internal energy,

that is D

T ≥ 0, but internal energy cannot be converted back again, that is,

we can never have D

T < 0 with strict inequality. Once kinetic energy has

been turned into internal energy it is “lost” and cannot be retrieved. If we

drop a bucket of water to the ground it will heat up, but it cannot lift itself

166 19 G2 for Euler

2.5 3 3.5 4 4.5 5 5.5

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

1.4

Fig. 19.10. The mean value of the dissipation intensity of G2 in the turbulent wake

of the ﬂow around a surface mounted cube (see Chapter 33), vs log

of the number

of mesh points.

by cooling oﬀ. This is an example of irreversibility imposed by the 2nd Law,

to which we will return in more detail in Part VI of this book on Loschmidt’s

Mystery.

We prove below that a G2 solution weakly satisﬁes the 2nd Law, and thus

that ”G2 follows Physics”. We will in Part VI turn this around and ask if

“Physics follows G2?”.

In short, we can write the 2nd Law in the form dT ≥ 0 with dT = D

T .

In Part VI we show that the 2nd Law for compressible ﬂow generalizes to

dT + pdV ≥ 0 with dV representing change of volume. In compressible ﬂow

T may decrease under expansion with dV > 0.

19.11 A Global Form of the 2nd Law

Using (19.8) we can reformulate the basic energy estimate for NS equations

(16.2) as the following global form of the 2nd Law:

(

t )k

E(u

, p

) dxdt ≈

, (19.9)

indicating that for a dissipative weak Euler solution actually

19.13 Proof that EG2 is a Dissipative Weak Solution 167

(

t )k

, (19.10)

with substantial loss of total kinetic energy for a turbulent solution. A G2

solution has the same property by the basic energy estimate (19.3). The global

form of the 2nd Law states that in an isolated system without forcing the total

kinetic energy can only decrease and so does for turbulent ﬂow.

19.12 Understanding a Basic Fact

We realize that the quantities of signiﬁcance and interest are turbulent dis-

sipation and generation of heat energy. Our computations show that these

quantities are largely independent of the mesh size h as soon as it is rea-

sonably small, which may be viewed as an independence of (small) values of

viscosity and heat conductivity. We presented evidence in Fig. 19.10.

We understand that the motivation to seek to determine viscosity and heat

conductivity coeﬃcients has been to compute dissipation and heat generation.

If now these quantities can be directly computed, then we are relieved from

the diﬃcult (or hopeless) task of determining coeﬃcients of viscosity and

conductivity. We are led to the conclusion that the mere concept of coeﬃcients

of viscosity and heat conductivity is questionable form a scientiﬁc point of view

since we can never determine relevant values of these coeﬃcients, and even if

we could they would not be useful, since they would be overshadowed by the

numerical dissipation.

19.13 Proof that EG2 is a Dissipative Weak Solution

Choosing ˆv = (φ

∈

in EG2 according to (16.4), where φ is a positive

test function and the superscript h indicates interpolation into

, we get

assuming

U is bounded

U)φ dxdt = ((hφR(

U), R(

U)) + ((R(

U), (φ

− φ

U))

+((hR(

U), R((φ

) − R(φ

U))) +

where

R ≥ −C

√

h with C > 0 depending on ﬁrst order derivatives of φ and

the maximum of

U. We now use so-called super-approximation to obtain

kφ

U − (φ

k ≤ Chk

Uk,

with the notable feature that we gain one power of h without paying any ﬁrst

derivative price on

U. This is because φ

U is the product of a smooth function

and a function in the ﬁnite element space

V . Combined with the basic energy

estimate bounding k

√

hR(

U)k, it follows that

168 19 G2 for Euler

U)φ dxdt ≥ −C

√

which proves that G2 is a dissipative weak solution, as desired. This represents

one of the most important proofs in the book. Notice that we assume

U to be

bounded but not derivatives of

U, which would make the proof meaningless.

Summary of Mathematical Aspects

My feeling is that many mathematicians and graduate students are intrigued

by what they hear about problems of the mechanics of an incompressible

ﬂuid, but don’t study them because they don’t know enough physics and

fear to make fools of themselves. What they don’t know, I think, is how

abysmally little we actually know about ﬂuids, and how it would be hard to

act more the fool than many have already done. I believe the diﬃculty arises

ﬁrst, over an inﬂated nomenclature that burdens the subject and, second,

over a lack of understanding about how ignorant we can be in our technolog-

ical society and how close to the surface many problems lie.... In spite of the

profound mathematical methods we use to attack the problems, we know

very little about ﬂuids, we can tell the physicist almost nothing of what he

wants to know, and interesting problems abound. (Marwin Shinbrot, 1973)

Our consciousness does not reﬂect the molecular chaos of the phenomena

but exerts an integrating function with respect both space and time, from

results the apparent homogeneity and continuity of the phenomena. (Weyl)

Blind fate could never make all the planets move one and the same way in

orbs concentric. (Newton)

20.1 Outputs of -weak Solutions

We have introduced the concept of -weak solutions to the NS equations. To es-

timate the diﬀerence in output of two -weak solutions ˆu and ˆw, M (ˆu)−M( ˆw),

with M(ˆu) ≡ ((ˆu,

ψ)) deﬁned by a function

ψ, we introduced a linearized dual

problem with coeﬃcients depending on u and w and estimated derivatives of

the solution of the dual problem in a corresponding stability factor S



(

ψ), to

get

|M(ˆu) −M( ˆw)| ≤ 2S



(

ψ).

We next noted that a G2-solution

U is an C

khR(

U)k-weak solution, and

this way we obtained an a posteriori output error estimate of the form

170 20 Summary of Mathematical Aspects

|M(ˆu) −M(

U)| ≤ ( + C

khR(

U)k)S



(

ψ),

with S



(

ψ) a corresponding stability factor, and 

= C

khR(

U)k. Sim-

plifying, assuming  small (and C

≤ 1), the a posteriori error estimate took

the form

|M(ˆu) −M( ˆw)| ≤ khR(

U)kS

(

ψ), (20.1)

and the corresponding stopping criterion was

khR(

U)kS

(

ψ) ≤ T OL.

If the stability factor S

(

ψ) is not too large and the tolerance T OL not too

small, then we may be able to reach the stopping criterion with available

computer power.

We have pointed out a basic feature of the a posteriori error estimate result-

ing from the properties of G2, namely the presence of the factor h multiplying

the residual R(

U). If S

(

ψ) is not too large, this means that we may reach the

stopping criterion without the residual R(

U) being pointwise small. We may

thus compute an accurate mean value output from a discrete solution with

a pointwise large residual. In a turbulent ﬂow we may expect (and actually

see in computations) that pointwise R(

U) ∼ h

−1/2

. This evidence strongly

indicates that the mere idea of a pointwise solution to a turbulent ﬂow will

have to be refuted. As already pointed out above, this is in direct opposition

to the Clay Institute formulation of its Prize Problem concerning existence,

regularity and uniqueness of pointwise solutions to the NS equations.

20.2 Chaos and Turbulence

We have been led to the following essential aspects of a dynamical system with

chaotic solutions such as the NS equations: (i) strong sensitivity of pointwise

outputs, (ii) weak sensitivity of mean value outputs, and (iii) weak sensitivity

of stability factors.

To identify these features for a given dynamical system, we would ﬁrst

compute one trajectory u(t) pointwise. We would then solve the corresponding

dual problem linearized at u(t) with data corresponding to pointwise output

to ﬁnd a large stability factor, and with data corresponding to a mean value

output to ﬁnd a stability factor which is not large. This would give evidence

of (i) and (ii). In particular we would get the information that the mean value

output would be insensitive to solution perturbations, and thus that we could

expect to be able to compute the mean value output from only one solution

trajectory.

There would be one piece of information missing, namely (iii) which rep-

resents insensitivity of the mean value stability factor to the choice of solution

trajectory underlying the linearization in the dual problem. To get evidence

of this insensitivity, we would have to compute a couple of diﬀerent solutions

20.4 Irreversibility 171

u(t) by introducing some perturbations and then solve the corresponding dual

problems. The evidence would then be that the corresponding stability fac-

tors would be insensitive to the perturbations. In particular, we would get the

signal that the more precise nature of the perturbations would be insigniﬁcant.

In this book we present evidence that turbulent ﬂow has the features (i)-

(iii) and thus carries the basic features of the type of chaos we suggest above.

The result is that a mean-value output may be observable/computable to

a tolerance of interest under statistical perturbations of input of unknown

nature, while a point value is not.

In a turbulent ﬂow a lot of detailed information is destroyed in dissipation,

which thermodynamically connects to a substantial increase of entropy. In

order for a mean value in turbulent ﬂow to be well deﬁned, it cannot have

other than a weak dependence on the destroyed information, and indeed we

observe this to be a real phenomenon since we ﬁnd mean value aspects of

turbulent ﬂow to be computable without resolving all details of the ﬂow. Thus

certain aspects of turbulent ﬂows may be computable, in fact, sometimes more

easily computable than laminar ﬂows, which may show a stronger dependence

on details.

This is in contrast to a conventional standpoint, where turbulent ﬂow may

seem to be uncomputable without turbulence models, which are diﬃcult if

not impossible to design. In this book thus we give concrete evidence that

turbulent ﬂow is computable, in fact often computable on a PC within hours.

20.3 Computational Turbulence

We have pointed out that the secret of computational turbulence is to under-

stand how it may be possible to compute mean value outputs, while point-

value outputs are not computable. We have noted that this can be explained

by the stability properties of the dual solution, which by cancellation eﬀects is

smaller for mean-value outputs than for point-values. Thus we may say that

the secret lies in the cancellation in the dual problem, which may be observed

to take place by simply computing the dual solution. We may also analyze

the cancellation eﬀect in simple model problems, but it seems impossible to

mathematically analyze this cancellation eﬀect in any realistic situation. Thus

we may get a glimpse of the secret, but we seem to be unable to capture the

whole truth by mathematical analysis. Our lives may carry a similar secret:

we may observe what we experience/compute as we go along and we may

understand some aspects, but the full truth will remain hidden.

20.4 Irreversibility

We have unfolded the secret of irreversibility in reversible systems in the

special case of incompressible inviscid ﬂow governed by the Euler equations

172 20 Summary of Mathematical Aspects

solved by G2. We have seen that the irreversibility is a necessary consequence

of the non-existence of stable pointwise solutions of the Euler equations and

the dissipative nature of G2 when computing approximate solutions. We may

phrase our result as a proof of the 2nd Law of thermodynamics from the 1st

Law combined with ﬁnite precision in the form of G2. We have remarked that

EG2 is a parameter-free mathematical model of (a part of) the World in the

spirit of Einstein.