Численные методы турбулентных несжимаемых течений (Том 4 Часть 2)

Подождите немного. Документ загружается.

16.4 A Posteriori Output Error Estimate for G2 135

16.4 A Posteriori Output Error Estimate for G2

We now let ˆu be an -weak solution of the NS equations and let

U be a G2-

solution, which we just showed can be viewed to be an 

-weak solution,

with 

= C

khR(

U)k >> .

As above we get the following a posteriori error estimate for a mean-value

output given by a function

ψ:

|M(ˆu) −M(

U)| ≤ ( + C

khR(

U)k)S



(

ψ), (16.8)

where S



(

ψ) is the corresponding stability factor deﬁned as above. Obviously

the size of the stability factor S



(

ψ) is crucial for computability: the stopping

criterion is evidently (assuming  small):

khR(

U)kS



(

ψ) ≤ T OL,

where T OL > 0 is a tolerance. If S



(

ψ) is too large, or T OL is too small, then

we may not be able to reach the stopping criterion with available computing

power, and the computability is out of reach.

Stability Aspects of Turbulence in Model

Problems

Merkw¨urdig ist auch das Versagen der Eindeutigkeitsbeweise in drei Di-

mensionen. Diese Fragen sind immer noch nicht befriedigend erkl¨art. Es

ist schwer zu glauben daß die Anfangswertaufgabe z¨aher Fl¨ussigkeiten f¨ur

n = 3 mehr als eine L¨osung haben k¨onnte, und der Erledigung der Ein-

deutigkeitsfrage sollte mehr Aufmerksamkeit geschenkt werden. (E. Hopf)

17.1 The Linearized Dual Problem

We have seen that the predictability/computability of a given ﬂow (solution

ˆu = (u, p) of the NS equations) is determined by the stability properties of

the corresponding linearized dual problem. We may thus say that the secret of

computational modeling of turbulent ﬂow is hidden in the stability properties

of the dual problem, which takes the following form when linearized around

the given velocity u, if we for simplicity leave out the pressure part of the dual

solution: Given ψ ﬁnd ϕ such that

− ˙ϕ − u · ∇ϕ + ∇u

ϕ − ν∆ϕ = ψ on [0,

t ), ϕ(

t ) = 0,

where (∇u

ϕ)

i=1

i,j

. This is a linear convection-diﬀusion-reaction

problem with convection velocity u and reaction coeﬃcient matrix ∇u and

data ψ. We are interested in the stability properties of the dual problem

which concern the size of the stability factor S = kϕk/kψk where k·k represent

some norms, usually diﬀerent, for ϕ and ψ. The stability factor S expresses

the sensitivity of an output related to ψ.

We now seek to estimate the size of the stability factor S for diﬀerent data

ψ corresponding to diﬀerent outputs. We seek qualitative understanding and

are thus ready to simplify. In reality, of course we just compute the stability

factor S and we do not need to understand anything, but we here seek some

rationale behind the computed values for S.

We then assume that the norm of kϕk, which typically involves derivatives

of ϕ, can be reﬂected through the size of ϕ itself through the coupling to

138 17 Stability Aspects of Turbulence in Model Problems

the viscous term in the dual equation. Eﬀectively, we may then leave out the

viscous term. Further, we note that the size of the dual solution ϕ does not

seem to be much aﬀected by the convection, since convection only shifts ϕ

in space but does not change its size. In contrast, the reaction term with

coeﬃcient ∇u

obviously may change the size of ϕ, and thus may aﬀect the

size of S. We thus focus on the stability properties of the reaction problem:

− ˙ϕ + Aϕ = ψ on [0,

t ), ϕ(

t ) = 0,

where the matrix A = ∇u

depends on (x, t). We are interested in the size

of the dual solution ϕ for diﬀerent ψ. In a turbulent ﬂow A may have large

coeﬃcients which may change rapidly with (x, t). In general we may expect

that the growth properties of ϕ connect to the spectrum of A with exponen-

tial growth corresponding to eigenvalues with negative real part, exponential

decay to eigenvalues with positive real part, and oscillations corresponding to

the imaginary part of conjugate pairs of eigenvalues.

Let us now freeze x and let λ

(t), i = 1, 2, 3, be the eigenvalues of A(x, t).

By (approximate) incompressibility of u and the fact that the sum of the

eigenvalues of a matrix is equal to the sum of its diagonal elements, we have

that

i=1

Real part(λ

) ≈ 0,

see Fig. 17.1, and thus we may expect that the exponential growth and decay

from the real parts of the eigenvalues will balance with no net growth, if we

let ϕ convect over diﬀerent x with the convection velocity u.

It remains to understand the possible eﬀect of the oscillating nature cou-

pled to the imaginary part of the conjugate eigenvalues. We shall see that

this connects to the observation that stability factors decrease as the length

of the mean values in time increases, which we could address to cancellation

in integrals of oscillating functions. We ﬁrst present a model case with a pair

of conjugate imaginary eigenvalues, in which case the dual problem for each

x is just the harmonic oscillator.

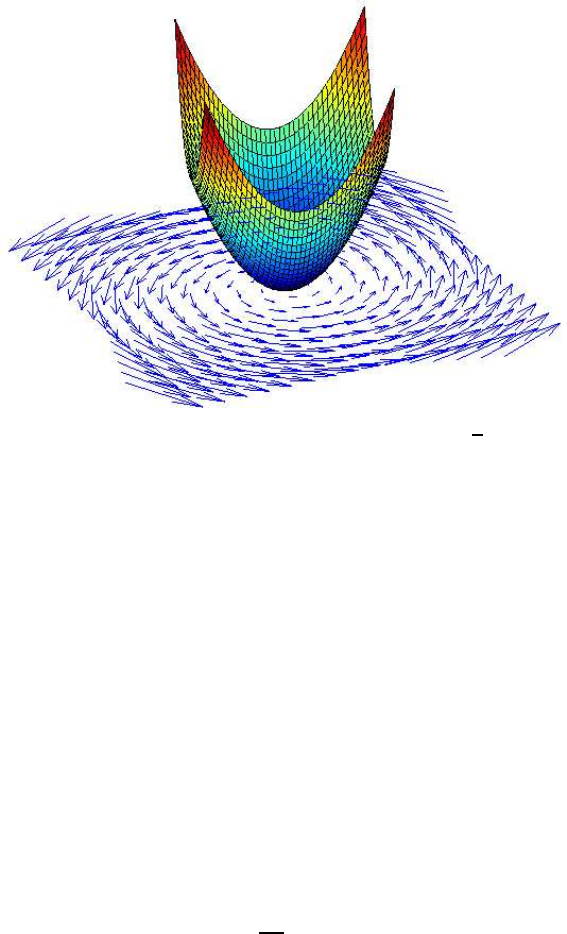
17.2 Rotating Flow

We consider a ﬂow corresponding to one rotating vortex tube oriented in the

-direction given by the stationary ﬂow ˆu = (u, p) such that

u(x) = ω(−x

, x

, 0), p =

+ x

which satisﬁes the NS equations with ν = 0 and f = 0, see Fig. 17.2. Here

ω is a moderately large positive number which represents the angular rota-

tional velocity of the vortex tube. We may think of the vortex tube having a

diameter 1/ω, and we may, very loosely speaking, think of a turbulent ﬂow as

17.2 Rotating Flow 139

200 400 600 800 1000 1200 1400 1600 1800

−6

−4

−2

0 500 1000 1500 2000 2500 3000 3500

−5

−4

−3

−2

−1

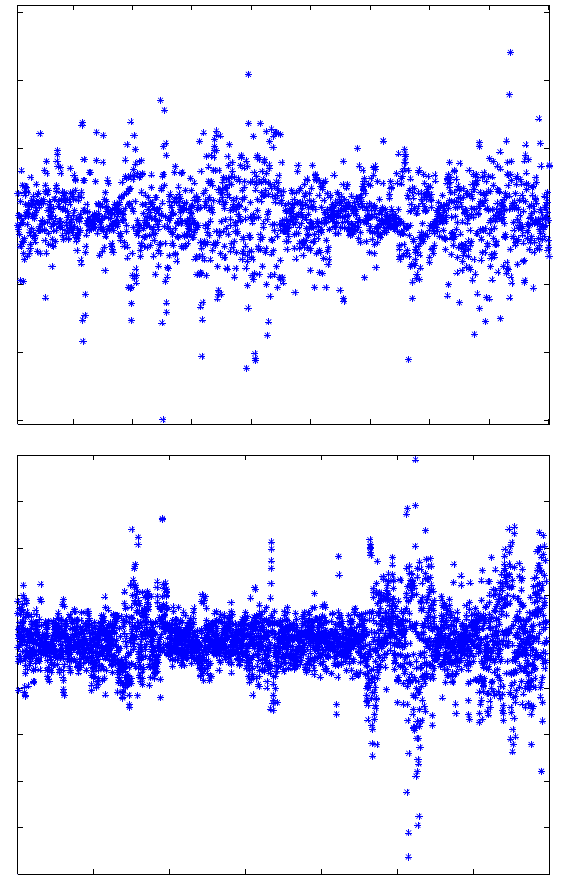
Fig. 17.1. Sum of the real parts of the eigenvalues of ∇U, for G2 solutions

U for

a few thousand elements in the turbulent wake of a circular and a square cylinder,

from computations presented in detail in Chapter 33.

140 17 Stability Aspects of Turbulence in Model Problems

a collection of such rotating tubes. Recalling that the velocity gradient of a

turbulent ﬂow would be of size ν

−1/2

, or h

−1/2

in a computational simulation

with smallest scale h, we could expect that ω ∼ ν

−1/2

or ω ∼ h

−1/2

Fig. 17.2. Rotational ﬂow u(x) = ω(−x

, x

, 0), and p =

+ x

17.3 A Model Dual Problem for Rotating Flow

The dual problem corresponding to rotating ﬂow takes the following form

disregarding the convection term and the ϕ

component as well as the space

dependence:

˙ϕ

+ ωϕ

= ψ

on (0,

t ],

˙ϕ

− ωϕ

= ψ

on (0,

t ],

(0) = ϕ

(0) = 0,

(17.1)

where we for simplicity reversed time with the transformation t →

t −t. This

is the model of a harmonic oscillator with frequency ω driven by the force

(ψ

, ψ

). We choose ψ

(t) = 1/∆

t for 0 ≤ t ≤ ∆

t, ψ

(t) = 0 for ∆

t < t ≤

and ψ

≡ 0, which (before time reversal) corresponds to the output

∆

) =

∆

t−∆

(t) dt, (17.2)

17.4 A Model Dual Problem for Oscillating Reaction 141

which is a mean value in time of length ∆

Writing (17.1) in matrix form as ˙ϕ + Aϕ = ψ on [0,

t ], ϕ(0) = 0, where

ϕ = (ϕ

, ϕ

) and A has a pair of imaginary eigenvalues ±iω, we can express

the solution ϕ(t) as a convolution of the data ψ(t) with the the fundamental

solution matrix exp(tA) of the homogeneous problem ˙ϕ + Aϕ = 0, as

ϕ(t) =

exp((t − s)A)ψ(s) ds.

Since exp(tA)

= cos(ωt), we have for t ≤ ∆

(t) =

∆

cos(ω(t − s)) ds =

sin(ωt)

ω∆

and for t > ∆

(t) =

∆

cos(ω(t − s)) ds =

sin(ωt) −sin(ω(t − ∆

t ))

ω∆

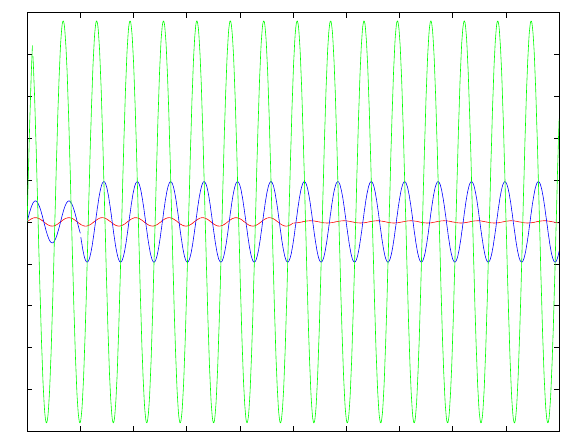
We now study the dependence of the magnitude of ϕ

(t) as a function of

the size ∆

t of the mean value. We ﬁnd that

|ϕ

(t)| ≈ 1 for ω∆

t ≤ 1,

|ϕ

(t)| ≈

ω∆

for ω∆

t large,

and we have that ϕ

(t) increases from zero with slope 1/∆

t as long as t <

min(∆

) and then levels oﬀ into oscillations, so that for ω∆

t large, ϕ

(t)

is much smaller than for ω∆

t small, see Fig. 17.3. A short mean value output

thus has a larger stability factor than a long mean value, which expresses that

a short mean value is more sensitive to perturbations than a long mean value

output.

Obviously, the reduction in size of the dual solution going from short to

long mean value comes from considerable cancellation in the integral deﬁning

(t) as a convolution of ψ(t) with the oscillating integrand cos(ωt), which

starts coming into play when ω∆

t > 1 and becomes more pronounced as ω∆

grows larger.

17.4 A Model Dual Problem for Oscillating Reaction

To model the eﬀect of the real parts of the eigenvalues summing to zero we

consider the scalar problem

− ˙ϕ(t) + cos(t)ϕ(t) = 0, on [0,

t ),

with solution

ϕ(t) = exp(sin(

t − t))ϕ(

t ).

Clearly, the net eﬀect of the oscillating reaction coeﬃcient cos(t) is very small:

ϕ(t) neither grows nor decays.

142 17 Stability Aspects of Turbulence in Model Problems

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Fig. 17.3. Model dual problem for rotational ﬂow; ω = 100, ∆

t = 0.01, 0.1, 0.5.

17.5 Model Dual Problem Summary

The dual problem for the NS equations is a convection-reaction-diﬀusion prob-

lem in space-time of the form

− ˙ϕ − u · ∇ϕ + ∇u

ϕ − ν∆ϕ = ψ on [0,

t ), ϕ(

t ) = 0.

Disregarding the diﬀusion and following the streamlines deﬁned by the con-

vection, we can view this problem as a collection of reaction problems in time

of the form

− ˙ϕ + Aϕ = ψ on [0,

t ), ϕ(

t ) = 0,

where A(t) is a 3 ×3 matrix which varies in time as ∇u

(x, t) varies along a

streamline. The real parts of the eigenvalues of A(t) sum to zero for each t,

and the imaginary parts appear as complex conjugates. We have separately

analyzed the stability properties of such a system as aﬀected by (i) the real

parts of the eigenvalues, and (ii) the imaginary parts of eigenvalues. Assuming

the real parts to oscillate between negative and positive values, would give no

net production. Finally the eﬀect of the imaginary parts would by a cancel-

lation eﬀect make the dual solution decrease as the length of the mean value

increases. The net eﬀect would be that the stability factor is large for a small

mean value output, and small for a large mean value output. We now proceed

to check if we can see this type of qualitative behavior by computing the dual

solution for a turbulent ﬂow.

17.7 Duality for a Model Problem 143

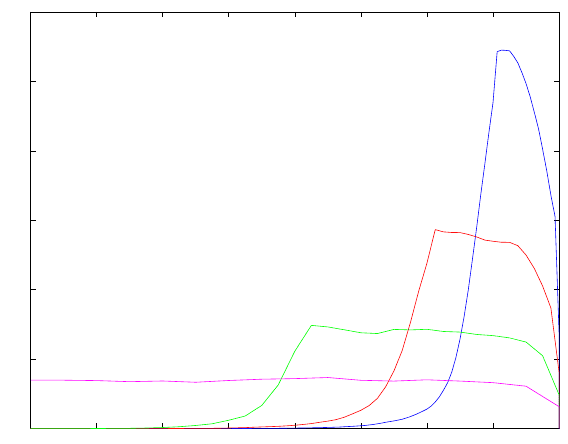
17.6 The Dual Solution for Bluﬀ Body Drag

In Fig. 17.4 we plot the dual solutions for mean values of the momentary drag

D(t) of the surface mounted cube for diﬀerent lengths of the mean values.

We see that these curves behave just like the ones we just presented for the

model cases of the harmonic oscillator and the oscillating reaction coeﬃcient

problem, except for the fact that in the bluﬀ body problem the dual solution

is “swept out” of the computational domain after some time resulting in a

decay to zero of the dual solution for larger times. Further, in the bluﬀ body

problem we measure derivatives of the dual solution and thus the stability

factors are larger than in the model problem, but their relative size follow the

pattern of the model.

2 2.5 3 3.5 4 4.5 5 5.5 6

500

1000

1500

2000

2500

3000

Fig. 17.4. Surface mounted cube: time series of k∇ϕk (with the time running

backwards), where the dual solutions corresponds to mean values of size 0.5,1,2,4.

17.7 Duality for a Model Problem

We illustrate the use of duality for error representation in the setting of a

dynamical system ˙u = f(u) on [0,

t ], u(0) = 0, with f : R → R. We consider

two solutions u(t) and v(t) with diﬀerent initial values u(0) and v(0). We want

to analyze the diﬀerence in output M

∆

(u)−M

∆

(v), where M

∆

(u) is deﬁned

144 17 Stability Aspects of Turbulence in Model Problems

in (17.2), resulting from the diﬀerence u(0) − v(0) in initial value, assuming

we solve the dynamical system for u(t) and v(t) exactly.

By integration by parts we obtain the following representation

∆

(u) − M

∆

(v) = ϕ(0)(u(0) − v(0))

where the dual solution ϕ(t) solves the linear problem

− ˙ϕ + f

(t)ϕ = ψ on [0,

t ), ϕ(

t ) = 0,

with ψ = 1/∆

t on [

t − ∆

t ] and ψ = 0 else, and

(t) =

f(su(t) + (1 − s)v(t)) ds.

Clearly ϕ(0) is the stability factor expressing the sensitivity of the output

mean value M

∆

(u) to changes in input initial value u(0). We can compute

ϕ(0) by ﬁrst computing the two trajectories u(t) and v(t) forward in time,

and then solving for the dual solution ϕ(t) backwards in time to the initial

time t = 0 to get ϕ(0).

17.8 Ensemble Averages and Input Variance

Although we do not in this book consider statistical approaches to turbulence,

we will make a comment on ensembles of solutions corresponding to ensembles

of data. We do this to exhibit an aspect of the dual problem which is of

key importance to understand that a mean value output may be moderately

sensitive to changes in input mean values, while it may be less sensitive to

input variance. This means that if outputs are mean values, then we do not

need information on input variance or the statistical distribution of input.

This is crucial since usually information on input variance or distribution is

lacking. The only thing we can hope for in such a case is that a mean value

output such as drag is relatively insensitive to input variance.

We consider two solution ensembles u(t; i) and v(t; i) with initial values

u(0; i) and v(0; i), i = 1, ...N, in the setting of a dynamical system ˙u = f(u)

on [0,

t ], u(0) = 0, with f : R → R. For an ensemble w(i), i = 1, ..., N, we

introduce the mean value

w and deviation w

(i), i = 1, ..., N , deﬁned by

w =

i=1

, w

(i) = w(i) − w,

assuming a uniform density for the ensemble. Using duality we have the fol-

lowing representation for the time mean value M

∆

deﬁned above:

∆

(u) − M

∆

(v) =ϕ(0)



u(0) − v(0)



i=1

(0; i)(u

(0; i) −v

(0; i))