Численные методы турбулентных несжимаемых течений (Том 4 Часть 2)

Подождите немного. Документ загружается.

19.4 Drag of a Square Cylinder 155

-direction, subject to a uniform inﬂow velocity (1, 0, 0). We use slip bound-

ary conditions both on the cylinder and the channel walls. We use a locally

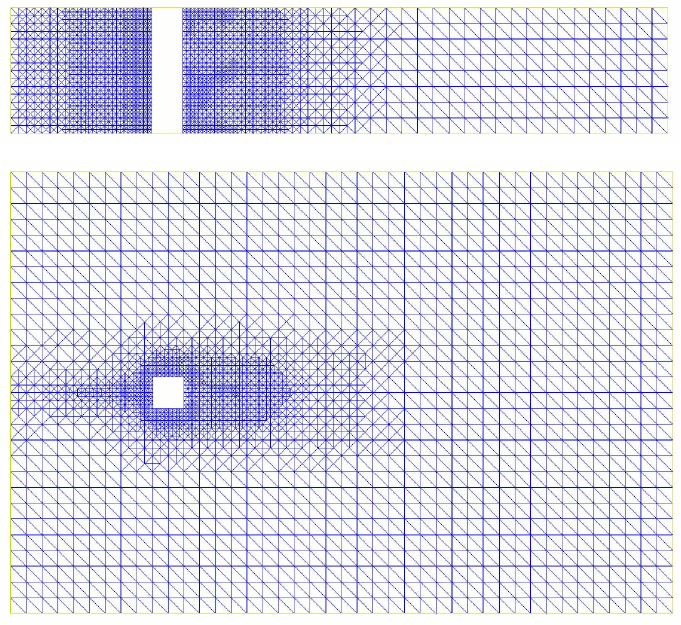
reﬁned tetrahedral mesh with 86 904 mesh points, shown in Fig. 19.2. The

advantage of using a square cylinder, instead of the circular cylinder studied

in Chapter 12, is that separation occur at the upstream corners and thus do

not change position with decreasing viscosity or mesh size.

Fig. 19.2. Computational mesh in the x

-plane (upper) and the x

-plane

(lower).

We ﬁrst determine an (approximate) stationary irrotational solution, not

by solving the Euler equations, but looking for a stationary velocity u = ∇φ

given by a potential φ(x

, x

), where φ = φ(x

, x

) is constant in x

and

solves Laplace’s equation ∆φ = 0 in the domain of the ﬂuid with ∇φ ·n = −1

at inﬂow, ∇φ · n = 1 at outﬂow, and with homogeneous Neumann conditions

∇φ · n = 0 on the channel walls and the cylinder, with n the outward unit

normal. Such a velocity u = (u

, u

, 0) is irrotational, and since the rotation

156 19 G2 for Euler

of (u · ∇)u vanishes (and by symmetry the circulation

u · ds = 0 with Γ

the intersection of the cylinder with the x

= 0 plane), there is a pressure p

such that (u ·∇)u + ∇p = 0. In other words, ˆu = (u, p) is a stationary laminar

solution of the Euler equations with irrotational velocity u and with u ·n = 0

on the channel walls and the cylinder surface with approximately equal inﬂow

and outﬂow velocities (since u

and u

are small on inﬂow and outﬂow). The

drag of ˆu is close to zero by the above argument.

Thus ˆu represents a laminar solution with pointwise residual close to zero

and with close to zero drag. By increasing the length of the channel, we can

reduce the pointwise residual to any size. Alternatively, by taking the inﬂow

velocity equal to that given by the potential φ, we have an exact solution to

Euler equations with close to zero drag.

In practice we compute φ by solving ∆φ = 0 using piecewise linear ﬁnite

elements in the three-dimensional ﬂuid volume, and then associate a corre-

sponding piecewise linear velocity U

= ∇φ by interpolation of the piecewise

constant ∇φ to the nodes in the mesh. This produces an approximate poten-

tial solution

with R(

) being small pointwise except close to the edges

of the cylinder.

We compute an approximate solution

U = (U, P ) to the Euler equa-

tions with initial velocity and inﬂow data given by

using G2 in the form

cG(1)cG(1) with continuous linear trial functions in space-time (see Chap-

ter 28). We ﬁnd that the computed velocity U(t) remains close to

only

for a few time steps, then develops non-symmetry in x

while maintaining

two-dimensionality after which it successively develops into a fully three-

dimensional turbulent solution which is far from irrotational. This turbulent

solution is similar to the turbulent solution of NS equations with small viscos-

ity and with no slip boundary conditions on the cylinder presented in [59, 53].

For the Euler equations we compute the drag coeﬃcient, which is close to the

value 2.2 obtained for the NS equations with viscosity ν = 10

−6

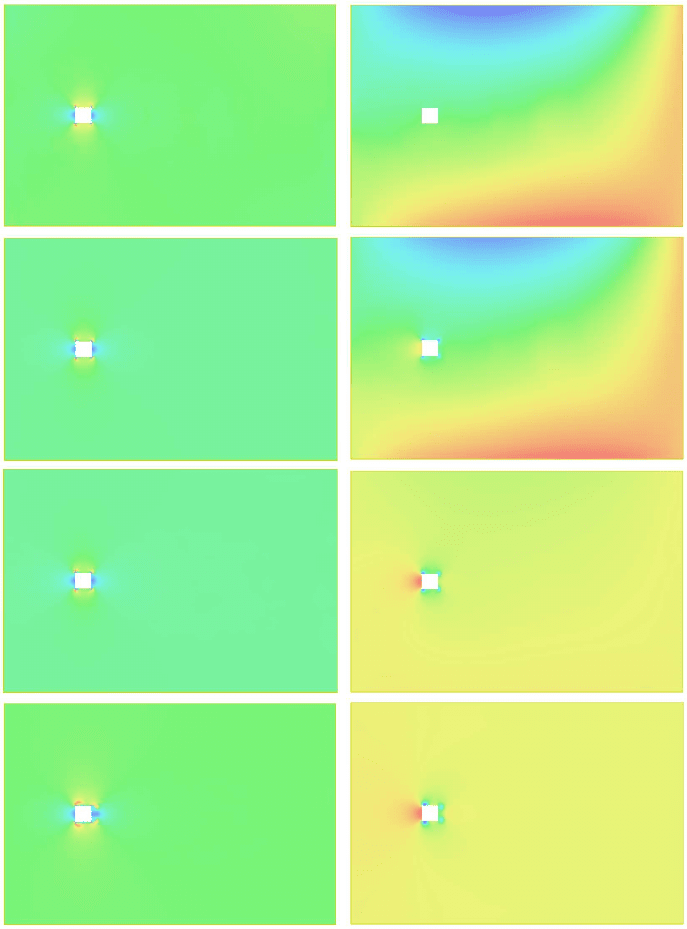
In Fig. 19.3 we plot the solution (U, P ) for the ﬁrst few time steps, using

a very small time step of size 0.1 times the smallest element diameter in

the mesh. We ﬁnd that the instability of the the initial symmetric solution

U(0) = ∇φ is ﬁrst expressed in a ﬂuctuating pressure until a high pressure

in front of the cylinder is established, which initializes the development of a

non-symmetric velocity eventually going turbulent.

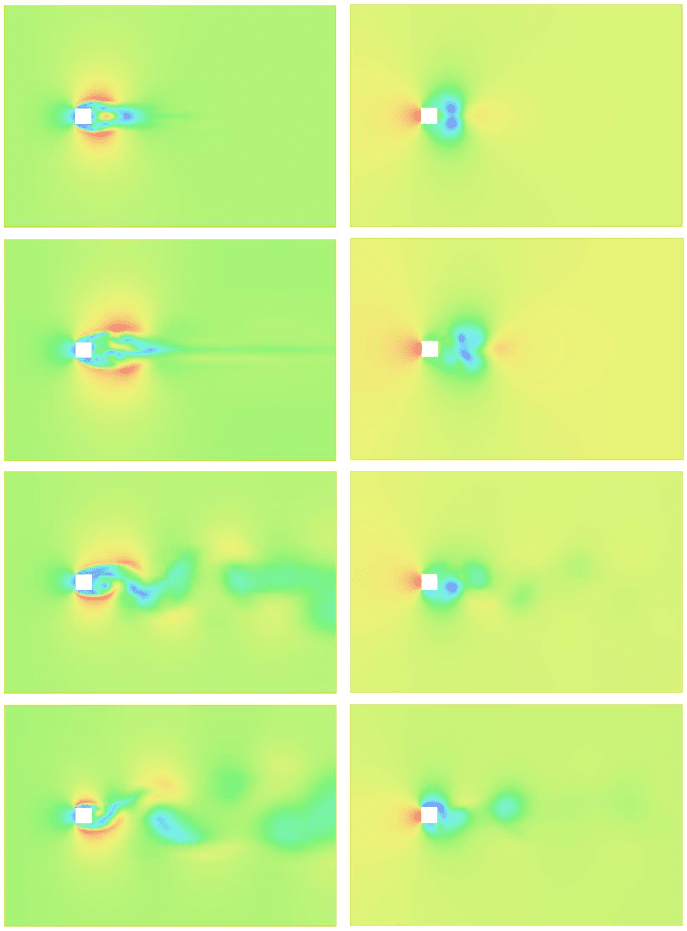
In Fig. 19.4–19.6 we show results starting with zero initial velocity, using

now time steps of the same size as the ﬁnest element diameter in the mesh.

We ﬁnd again the potential solution during the ﬁrst few time steps with the

same development into a turbulent solution.

19.5 Instability of the Potential Solution

We also illustrate the instability of the potential solution by solving the dual

Euler equations, linearized at the potential solution and the developed turbu-

19.5 Instability of the Potential Solution 157

Fig. 19.3. Magnitude of the computed velocity (left) and pressure (right) from

initial data U (0) = ∇φ, for time steps no 2,5,7,37.

158 19 G2 for Euler

Fig. 19.4. Magnitude of the computed velocity (left) and pressure (right) corre-

sponding to zero initial data, for time steps 4,6,8,32.

19.5 Instability of the Potential Solution 159

Fig. 19.5. Magnitude of the computed velocity (left) and pressure (right) corre-

sponding to zero initial data, for time steps 64,128,704,1024.

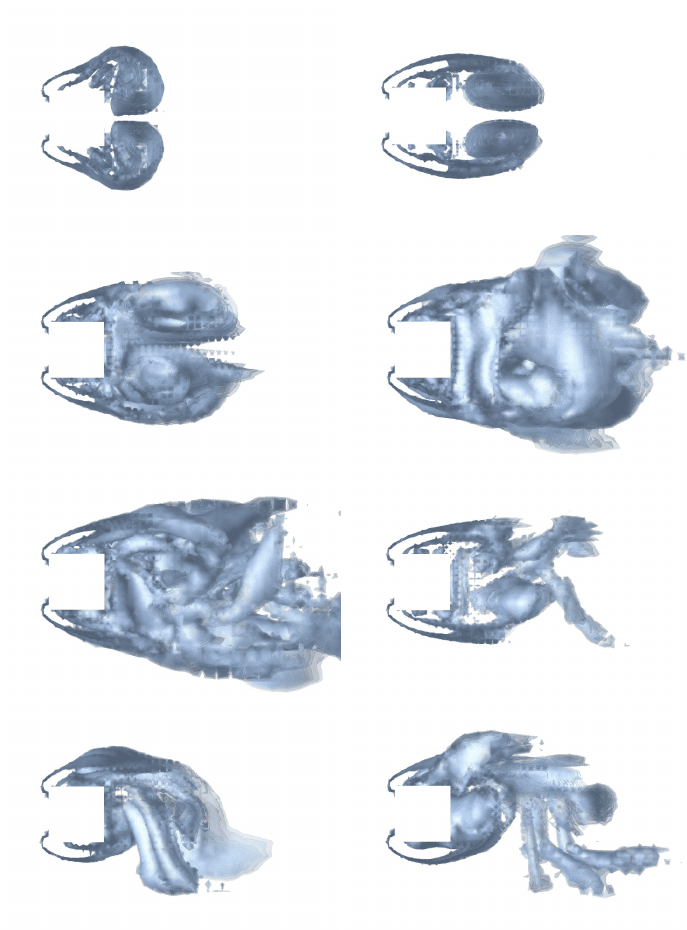
160 19 G2 for Euler

Fig. 19.6. Magnitude of the vorticity corresponding to zero initial data, for time

steps 48,64,96,128,160,704,960,1024.

19.5 Instability of the Potential Solution 161

lent ﬂow respectively. We use as data to the dual problem a source term in

the dual velocity equation being a characteristic function over a cube in space

of side length 0.025 centered at (0.6,0.7,0.2), times 0.025

−4

. The source term

acts over a time interval of length 0.025 from the ﬁnal time (start time in the

dual equation), corresponding to the computation of a small space-time mean

value at ﬁnal time.

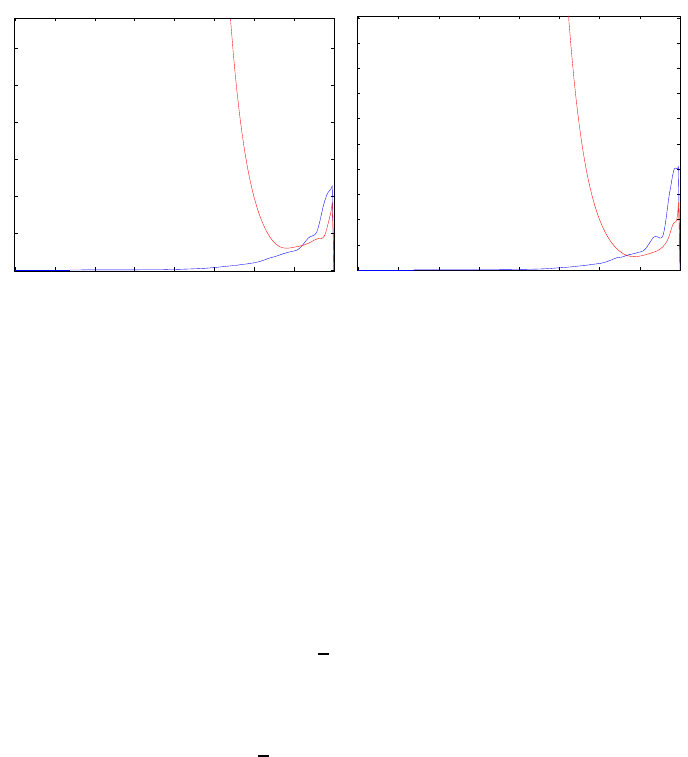
In Fig. 19.8 we ﬁnd that the dual solution corresponding to linearization at

the potential solution grows exponentially, whereas linearized at the turbulent

solution the dual solution shows a slow growth followed by decay to zero.

This reﬂects the instability of the potential solution, being extremely sensitive

to perturbations at earlier times, and the destruction of information in the

turbulent ﬂow making the solution insensitive to perturbations with respect

to the mean value output. We plot the two dual solutions in Fig. 19.7.

Fig. 19.7. Dual velocity |ϕ|, linearized at U (0) = ∇φ (upper), and linearized at

turbulent ﬂow (lower), for time t = 17.5, 17.

162 19 G2 for Euler

14 14.5 15 15.5 16 16.5 17 17.5 18

100

200

300

400

500

600

14 14.5 15 15.5 16 16.5 17 17.5 18

x 10

Fig. 19.8. The L

-norm of the dual velocity (left) and dual velocity gradient (right),

linearized at U (0) = ∇φ and turbulent ﬂow respectively.

19.6 Temperature

We recall the general Euler equations (4.1) including the equation expressing

conservation of the total energy:

˙e + ∇ · (eu + pu) = 0, in Q, (19.4)

where with ρ = 1 the total energy e is given by

e =

|u|

+ T, (19.5)

where T is the temperature. We can write (19.4) as

T = −D



|u|



− ∇p · u ≡ E(u, p), in Q, (19.6)

where D

T =

T + (u · ∇)T is the convective derivative of T based on the

velocity u. We note that for a pointwise solution (u, p) of (19.1) with f = 0, we

have E(u, p) = 0, which follows by multiplication of the momentum equation

by u. However, we know that (stable) pointwise solutions do not exist, so we

cannot say that E(u, p) = 0.

Nevertheless, having computed ˆu = (u, p) from the incompressible Euler

equations, we can solve for the total energy e in the linear equation (19.4)

with u and p given, to obtain the internal energy/temperature T from (19.5).

Alternatively, we can solve for the internal energy T in (19.6) with the right

hand side E(u, p) given. In Fig. 19.9 we show the computed total energy,

and the corresponding temperature starting from zero temperature at initial

time and letting the inﬂow temperature be equal to zero. We notice that the

19.6 Temperature 163

Fig. 19.9. Total energy e (left) and temperature T (right); t = 4.5, 5.5, 11, 16.

164 19 G2 for Euler

temperature is elevated in the turbulent wake, with the heat being generated

by the turbulent dissipation (represented by the weighted least squares term

in G2). We notice that the generated heat is transported by the turbulent

velocity u in a process of turbulent diﬀusion of heat, which most likely will

dominate any molecular diﬀusion of heat (which we eﬀectively set to zero in

the computation). We are thus able to compute a temperature distribution in

a turbulent ﬂow with the only information that the coeﬃcients of viscosity and

molecular heat diﬀusion are very small. This is very good news since precise

quantitative determination of very small viscosities or heat conductivities is

very diﬃcult both theoretically and experimentally.

19.7 G2 as Dissipative Weak Solutions

The computations presented in Fig. 19.9 show that the temperature T is non-

negative, which we may connect to the sign of the right hand side E(u, p) in

(19.6): If E(u, p) ≥ 0 in Ω ×I, then necessarily T ≥ 0 in Ω×I if T (·, 0) = T

0. More precisely, (19.6) would then state that T can only increase following

the ﬂow. So can we guarantee that a G2 approximate weak solution (U, P )

satisﬁes (in a suitable weak sense)

E(U, P ) ≥ 0, in Q?

Yes, we can prove that

E(U, P )φ dxdt ≥ −C

√

h, (19.7)

for any non-negative test function φ, where C is a positive constant depending

on φ. We give a proof below.

19.8 Comparison with Viscous Regularization

The same question is similarly addressed by Duchon-Robert in [32], introduc-

ing the notion of a dissipative weak solution (u, p) to the Euler equations,

which is a function (u, p) satisfying the Euler equations in a weak sense, and

in addition satisﬁes the positivity condition E(u, p) ≥ 0 in Q in a weak sense.

The discussion starts from the observation that a strong (pointwise) solu-

tion (u, p) satisﬁes E(u, p) = 0 pointwise, as we remarked above. Further,

the observation is made that a limit (u, p) of the NS solutions (u

, p

) as the

viscosity ν tends to zero, will satisfy E(u, p) ≥ 0 weakly, as a consequence of

multiplying the momentum equation in NS equations by u

φ with φ(x, t) a

non-negative test function and integrating, to get

E(u

, p

)φ dxdt =

ν|∇u|

φ dxdt +

νu

∇u

· ∇φ

dxdt,