Численные методы турбулентных несжимаемых течений (Том 4 Часть 2)

Подождите немного. Документ загружается.

15.2 Uniqueness of c

and c

125

reﬁned computational meshes, with h the smallest element diameter in the

mesh.

We ﬁnd that S

(

ψ) shows a slow logarithmic growth, and extrapolating

we ﬁnd that S

(

ψ) ∼ ν

−1/2

. We take this as evidence of computability and

weak uniqueness of c

, and we obtain similar results for the lift coeﬃcient c

Fig. 15.2. Surface mounted cube: velocity |U | (upper) and pressure P (lower), in

the x

-plane at x

= 3.5H and in the x

-plane at x

= 0.5H.

126 15 Weak Uniqueness by Computation

Fig. 15.3. Surface mounted cube: dual velocity |ϕ

| (upper), and dual pressure |ι

(middle), in the x

-plane at x

= 3.5H and in the x

-plane at x

= 0.5H.

15.3 Non-Uniqueness of D(t)

We now investigate the computability and weak uniqueness of the normalized

drag force D(t) at a speciﬁc time t. In Figure 15.1 we show the variation in

time of D(t) computed on diﬀerent meshes, and we notice that D(t) for a

given t does not appear to converge with decreasing h: The best we can say

seems to be that 1.3 ≤ D(t) ≤ 1.7.

We now choose one of the ﬁner meshes corresponding to h

−1

≈ 500, and

we compute the dual solution corresponding to a mean value of D(t) over a

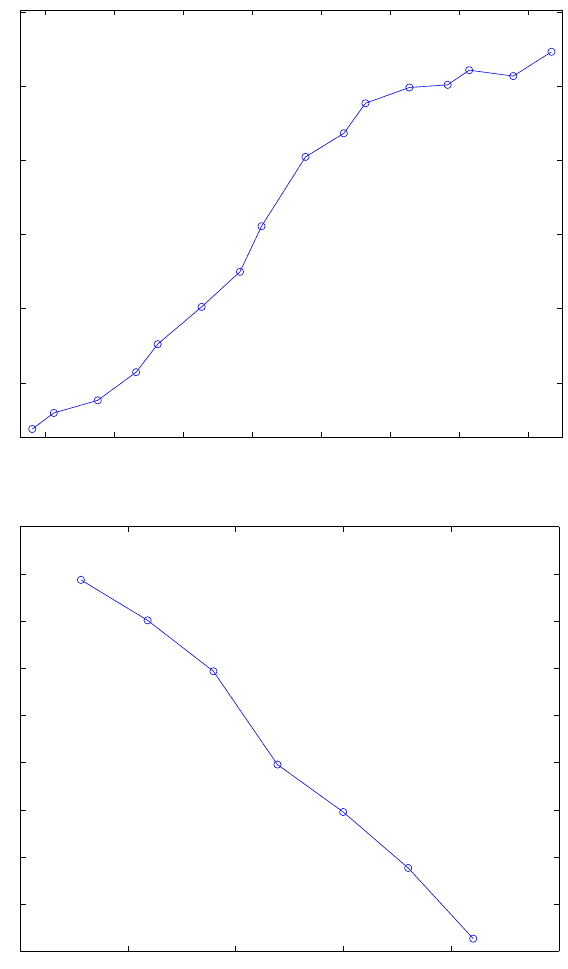
15.3 Non-Uniqueness of D(t) 127

0.8 1 1.2 1.4 1.6 1.8 2 2.2

2.2

2.4

2.6

2.8

Fig. 15.4. log

-log

-plot of S

(

ψ) as a function of 1/h.

−1.5 −1 −0.5 0 0.5 1

2.8

2.9

3.1

3.2

3.3

3.4

3.5

3.6

3.7

Fig. 15.5. S

(

ψ) corresponding to computation of the mean drag force (nor-

malized) over a time interval [

t ], as a function of the interval length |

t −

(log

-log

-plot).

128 15 Weak Uniqueness by Computation

time interval [

t ], where we let

→

t. We thus seek to compute the point

value D(

t ).

In Figure 15.5 we ﬁnd a growth of S

(

ψ) similar to |

t −

−1/2

, as

we let

→

t. The results show that for |

t −

| = 1/16 we have S

(

ψ) ≈

10ν

−1

, and extrapolation of the computational results indicate further growth

(

ψ), as

→

t and h → ν. We take this as evidence of non-computability

and weak non-uniqueness of D(

t ).

15.4 Stability of the Dual Solution with Respect to Time

Sampling

To get an idea of the dependence of stability factors on the primal solution

U used to compute the dual solution, we sample the coeﬃcients in the dual

problem with diﬀerent frequencies in time and compute the corresponding

dual solutions. In Table 5.1 we display diﬀerent norms of the dual solution

ˆϕ

and notice that diﬀerent sampling frequencies give very similar stability

factors, and in Fig. 15.6 we plot snapshots of diﬀerent dual solutions, again

very similar.

freq. kϕ

k k∇ϕ

k k ˆϕ

8 7.99 646 652

4 8.04 658 663

∗

8.14 679 684

2 8.23 693 698

1 8.35 744 749

Table 15.1. Surface mounted cube: Norms of the dual solution ϕ

linearized at

a primal velocity U sampled with diﬀerent frequencies (normalized by the inﬂow

velocity U

∞

= 1), with “4

∗

” being a translated sampling of “4” with the same

frequency.

15.5 Conclusion

We have given computational evidence of weak uniqueness of mean values

such as c

and c

and weak non-uniqueness of a momentary value D(t) of

the total drag. In the computations we observe this phenomenon as a con-

tinuous degradation of computability (increasing stability factor S

(

ψ)) as

the length of the time interval underlying the mean value decreases to zero.

Eﬀectively we seem to be able to compute c

and c

up to a tolerance of

roughly 0.05 taking mean values in time of length 10, while the variation of a

momentary value D(t) may be almost a factor 10 larger. Thus the distinction

15.5 Conclusion 129

Fig. 15.6. Surface mounted cube: snapshots of the dual velocity |ϕ

| sampled 4

times per time unit (upper), 2 times per time unit (middle), and once per time

unit (lower), corresponding to “4”, “2”, and “1”, in Table 15.1, in the x

-plane at

= 3.5H and in the x

-plane at x

= 0.5H.

130 15 Weak Uniqueness by Computation

between computability (or weak uniqueness) and non-computability (weak

non-uniqueness) may in practice be just one order of magnitude in output

error, rather than a diﬀerence between 0 and 1 (or ∞).

Of course, this is what you may expect to see in a quantiﬁed computational

world, as compared to an ideal mathematical world. In particular, we are

led to measure residuals of approximate weak solutions, rather than working

with the exact weak solutions of Leray with zero residuals. A such quantiﬁed

mathematical world is in fact richer than an ideal zero residual world, and

thus may be more accessible.

Existence of -Weak Solutions by G2

One may be tempted to believe that physical laminar ﬂows correspond

to smooth mathematical solutions (of the Navier–Stokes equations) and

turbulent ﬂows to non-smooth solutions (Oseen in Hydrodynamik ...).

On peut v´eriﬁer en outre que l’´energie cin´etique totale du liquide reste

born´ee; mais il ne semble pas possible de d´eduire de ce fait que le mouvement

lui-mˆeme reste r´egulier; j’ai mˆeme indiqu´e une raison qui me fait croire `a

l’existence de mouvements devenant irr´eguliers au bout d’un temps ﬁni; je

n’ai malheuresement pas r´eussi `a forger un exemple d’une telle singularit´e

(Leray 1934).

We will now discuss in a little more detail the Struggle for Existence.(Darwin)

16.1 Introduction

We now show that we may construct -weak solutions of the NS equations

using stabilized Galerkin ﬁnite element methods in the form of G2. We do

this in order to highlight a basic property of a G2 solution, which is designed

so as to have a a small residual in a weak sense, and thus may pass as an

-weak solution for a certain  depending on the mesh size. We do not here

give full details of the formulation of G2, e.g. concerning the use of continuous

or discontinuous Galerkin for the time stepping, but focus on the basic role of

the stabilization in G2, and give a complete description of G2 in Chapter 28.

In the discussion of the Clay Prize Problem we commented that an alterna-

tive way of proving existence of -weak solutions is to ﬁrst prove existence for

suitably regularized NS equations, which is possible using standard methods

of mathematical analysis, and to then prove that a regularized solution passes

as an -weak solution for some  depending on the regularization, which tends

to zero with the regularization.

132 16 Existence of -Weak Solutions by G2

16.2 The Basic Energy Estimate for the Navier–Stokes

Equations

We start by deriving a basic stability estimate of energy type for the velocity

u of the NS equations (5.3), assuming for simplicity that f = 0. This is about

the only analytical a priori estimate known for the NS equations. We thus

formally assume existence of a (pointwise) solution (u, p), and derive a bound

for the velocity u in terms of given data.

Scalar multiplication of the momentum equation by u and integration with

respect to x gives

Ω

|u|

dx + ν

i=1

Ω

|∇u

dx = 0,

because by partial integration (with boundary terms vanishing),

Ω

∇p · u dx = −

Ω

p∇ · u dx = 0

and

Ω

(u · ∇)u · u dx = −

Ω

(u · ∇)u · u dx −

Ω

∇ · u|u|

so that

Ω

(u · ∇)u · u dx = 0. (16.1)

Integrating next with respect to time, we obtain the following basic a priori

stability estimate for

t > 0 in terms of the L

-norm of the initial velocity u

(u) ≡

ku(·,

t )k

+ D

(u,

t ) =

, (16.2)

where

(u,

t ) = ν

i=1

k∇u

dt,

and where k· k denotes the L

(Ω)-norm. This estimate gives a bound on the

kinetic energy of the velocity with D

(u,

t ) representing the total dissipa-

tion from the viscosity of the ﬂuid over the time interval [0,

t ]. We see that

the growth of this term with time corresponds to a decrease of the velocity

(momentum) of the ﬂow (with f = 0).

The characteristic feature of a turbulent ﬂow is that D

(u,

t ) is compar-

atively large, while in a laminar ﬂow with ν small, D

(u,

t ) is small. With

(u,

t ) ∼ 1 in a turbulent ﬂow and |∇u| uniformly distributed, we may

expect to have pointwise

|∇u

| ∼ ν

−1/2

. (16.3)

16.3 Existence by G2 133

16.3 Existence by G2

To generate approximate weak solutions of the NS equations, we use a ﬁnite

element method of the form (assuming for simplicity f = 0): Find

U ≡

∈

, where

⊂

V is a ﬁnite dimensional subspace of piecewise polynomial

functions deﬁned on a computational mesh in space-time of mesh size h, such

that

((R(

U), ˆv)) + ((hR(

U), R(ˆv))) = 0, ∀ˆv ∈

, (16.4)

where R( ˆw) ≡ (R

( ˆw), R

(w)), ˆw = (w, r) and

( ˆw) = ˙w + U ·∇w + ∇r − ν∆w,

(w) = ∇ · w,

(16.5)

with element-wise deﬁnition of second order terms. We here interpret a con-

vection term ((U · ∇w, v)) as

((U · ∇w, v)) −

((U · ∇v, w)

which is literally true if ∇ · U = 0. With this interpretation we will have

((U · ∇U, U )) = 0, which corresponds to (16.1), even if the divergence of the

ﬁnite element velocity U does not vanish exactly. With this interpretation we

obtain choosing ˆv =

U in (16.4) (still assuming f = 0):

(U) + ((hR(

U), R(

U))) =

. (16.6)

Fig. 16.1. Richard Courant (1888–1972) introduced the ﬁnite element method in

1922, in an existence proof of a version of the Riemann mapping theorem. Boris Grig-

orievich Galerkin (1871–1945), Russian engineer who introduced the ﬁnite element

method as a computational tool.

The ﬁnite element method (16.4) is a stabilized Galerkin method with

the term ((R(

U), v)) corresponding to Galerkin’s method and the term

134 16 Existence of -Weak Solutions by G2

((hR(ˆu), R(ˆv))) corresponding to a weighted residual least squares method

with stabilizing eﬀect expressed in (16.6). We also refer to this method as

General Galerkin or G2, and we thus refer to

U as a G2-solution. The ex-

istence of a discrete solution

U ≡

∈ V

follows by Brouwer’s ﬁxed point

theorem combined with the stability estimate (16.6).

We now return to the main objective of this chapter of showing the exis-

tence of -weak solutions to the NS equations. For all ˆv ∈

V , we have with

ˆv

∈

a standard interpolant of v satisfying kh

−1

(ˆv −ˆv

)k ≤ C

kˆvk

, using

also (16.4),

((R(

U), ˆv)) = ((R(

U), ˆv − ˆv

)) − ((hR(

U), R(ˆv

)))

≤ C

khR(

U)kkˆvk

+ M (U)khR(

U)kkˆvk

(16.7)

where M(U ) is a pointwise bound of the velocity U(x, t), and C

≈ 1 is an

interpolation constant. It follows that the G2-solution

U is an -weak solution

with

 = (C

+ M (U))khR(

U)k ≤

√

h(C

+ M (U))ku

since from the energy stability estimate k

√

hR(

U)k ≤ ku

Assuming now that M(U ) = M(U

) is bounded with h > 0, and letting

+ M(U) ≤ C, it follows that

U is an -weak solution with  = C

√

assuming ku

k ≤ 1. More generally, we may say that a G2 solution

U is an

-weak solution with  = CkhR(

U)k.

We have now demonstrated the existence of an -weak solution to the

NS equations for any , assuming that the maximum computed velocity is

bounded (or grows slower than h

−1/2

). More generally, we have shown that a

G2-solution

U is an -weak solution with  = C

khR(

U)k with C

= C

M(U). Computing

U, we can compute  = C

khR(

U)k and thus determine

the corresponding .

We conclude that coming up with -weak solutions to the NS equations

is easy, if we use G2 and a computer (and ﬁnd that C

grows slower than

−1/2

We now turn to the question of estimation of the error in output of G2-

solutions, which of course as above will bring in the corresponding stability

factor.

Remark. In estimating above ((R(

U), ˆv−ˆv

)) we did not properly account for

the diﬀusion term ((ν∇U, ∇(v −v

))). Doing so would introduce an additional

term which most easily can be estimated by a term of the form C

√

νkˆvk

and to bound this term as above we would need that ν ≤ h. Since ν often is

smaller than 10

−4

for the problems we focus on in this book, this would not

be restrictive in most cases. For larger ν we can turn the argument around in

a diﬀerent way, but we do not here enter into details.