Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Несмотря на то, что материал данной главы в основном посвящен техническим аспектам

управления проектами (в частности составлению сетевых графиков проектов и отысканию

критического пути), не следует забывать об огромной важности менеджмента в этом процессе.

Успех любого проекта в значительной мере зависит от того, как работает проектная группа. Так,

например, Пол Уильяме (Paul В. Williams), который обучает управлению проектами сотрудников

J.P. Penny Company, неоднократно подчеркивал, насколько важным стимулятором успеха,

особенно на ранних его стадиях, является правильная организация работы над проектом.

В приведенной ниже врезке "Новация" перечислено десять основных причин, которыми, по

мнению г-на Уильямса, объясняется огромное значение правильного подхода к управлению

проектами. По его словам, если вы обнаружили, что работаете в конкретной группе или даже

руководите ею, это вполне может означать, что вы работаете или руководите каким-либо

проектом, даже не осознавая этого. Он также заявляет, что единственная разница между

руководством группой и руководством проектом заключается в том, что в первом случае усилия

направлены на выполнение определенных операций и соблюдение взаимосвязи между ними, а во

втором — на окончательный результат. Кроме того, по мнению г-на Уильямса, добившись успехов

в руководстве группой, менеджер, как правило, может рассчитывать на повышение по службе.

НОВАЦИЯ

Десять основных причин, почему важно правильное управление проектами

10. Организации, которые пошли на реализацию наскоро спланированного проекта с плохим

руководством, ослабляют себя и подвергают опасности увольнения своих служащих, так как при

этом они даром растрачивают свои драгоценные ресурсы.

9. Организации, находящиеся на переходном этапе (например, в процессе обновления

производства, сокращения объемов и т.д.), будут зависеть от проектов и их руководителей при

выполнении даже тех операций, которые раньше выполнялись их подразделениями.

8. За редким исключением все инициаторы проектов перекладывают ответственность за

недостатки в их реализации на плохое управление.

7. Достаточно принять одно-два неправильных решений, и ваша репутация пострадает

настолько, что потенциальные участники следующих этапов проекта откажутся от сотрудничества

с вами.

6. Работа над проектом часто "маскируется" выражением "работа в команде". Если вы в

определенный момент обнаружили, что работаете в группе людей или даже руководите ими,

знайте, что вы, по всей вероятности, вместе с другими трудитесь над реализацией какого-либо

проекта.

5. Способности, необходимые для правильной организации и успешной реализации проектов,

пригодятся и при выполнении других профессиональных обязанностей.

4. Успешное руководство проектом — наиболее простой способ доказать людям,

принимающим соответствующие решения, что вы достойны повышения по службе.

3. Самый лучший способ стимулировать эффективность руководства проектом заключается в

том, чтобы приводить настолько впечатляющие положительные примеры, что другие люди просто

не смогут работать хуже.

2. Руководители проектов редко добиваются успехов, если точно не знают, как это сделать.

1. Если вы не работаете все лучше и лучше, значит, вы работаете все хуже, так как с каждым

годом становитесь все старше.

Источник. Paul В. Williams, Getting a Project Done on Time: Managing People, Time, and Results

(New York: The American Management Association, 1996), p. ix.

Дефиниции в управлении проектами

Проект (Project) можно определить как последовательность взаимосвязанных операций,

направленных, как правило, на достижение конкретного значительного результата, и для их

выполнения требуется продолжительное время. Управление проектом (Project Management)

можно описать как процедуру планирования, распределения и регулирования ресурсов (трудовых,

материальных и оборудования) с учетом всех ограничений данного проекта (технических,

бюджетных и временных).

Проекты обычно рассматриваются как самостоятельный процесс, однако на практике многие

проекты могут повторяться и просто переноситься в другие условия или на другие виды

продукции, чем достигается совершенно иной результат. Так, например, строительная компания,

возводящая здания, или фирма, выпускающая продукцию небольшими партиями (супермощные

компьютеры, локомотивы, линейные ускорители и т.д.), вполне может рассматривать свою

деятельность как работу над отдельными проектами.

Каждый проект начинается с составления перечня работ (Statement Of Work — SOW).

Обычно это краткое описание основных задач проекта с перечислением всех операций, которые

должны быть выполнены, и дат начала и окончания этих операций. В перечень работ также часто

включены требования к бюджету на каждом этапе проекта и список письменных отчетов, которые

должны предоставляться в ходе его реализации.

Следующим элементом, вводимым в проект, является рабочее задание (Task). На его

выполнение отводится, как правило, не больше нескольких месяцев, и выполняется оно одной

группой. Иногда, если возникает необходимость представить проект более подробно, задание

разбивается на ряд подзаданий (Subtask).

Пакетом работ (Work Package) называют набор операций, объединенных в единую группу и

подлежащих выполнению одним организационным подразделением. Этот элемент также входит в

общую структуру проекта: в нем представлено описание операций, которые должны быть

выполнены в рамках данного пакета работ, указываются даты их начала и завершения, приводятся

бюджетные требования и критерии эффективности, а также выделяются этапы работ (Milestones),

выполняемые в определенные периоды времени. В качестве примера типичных этапов можно

привести следующие: стадия конструкторской разработки, изготовление опытного образца,

завершение испытаний опытного образца, изготовление и приемка опытной партии.

Структура работ проекта

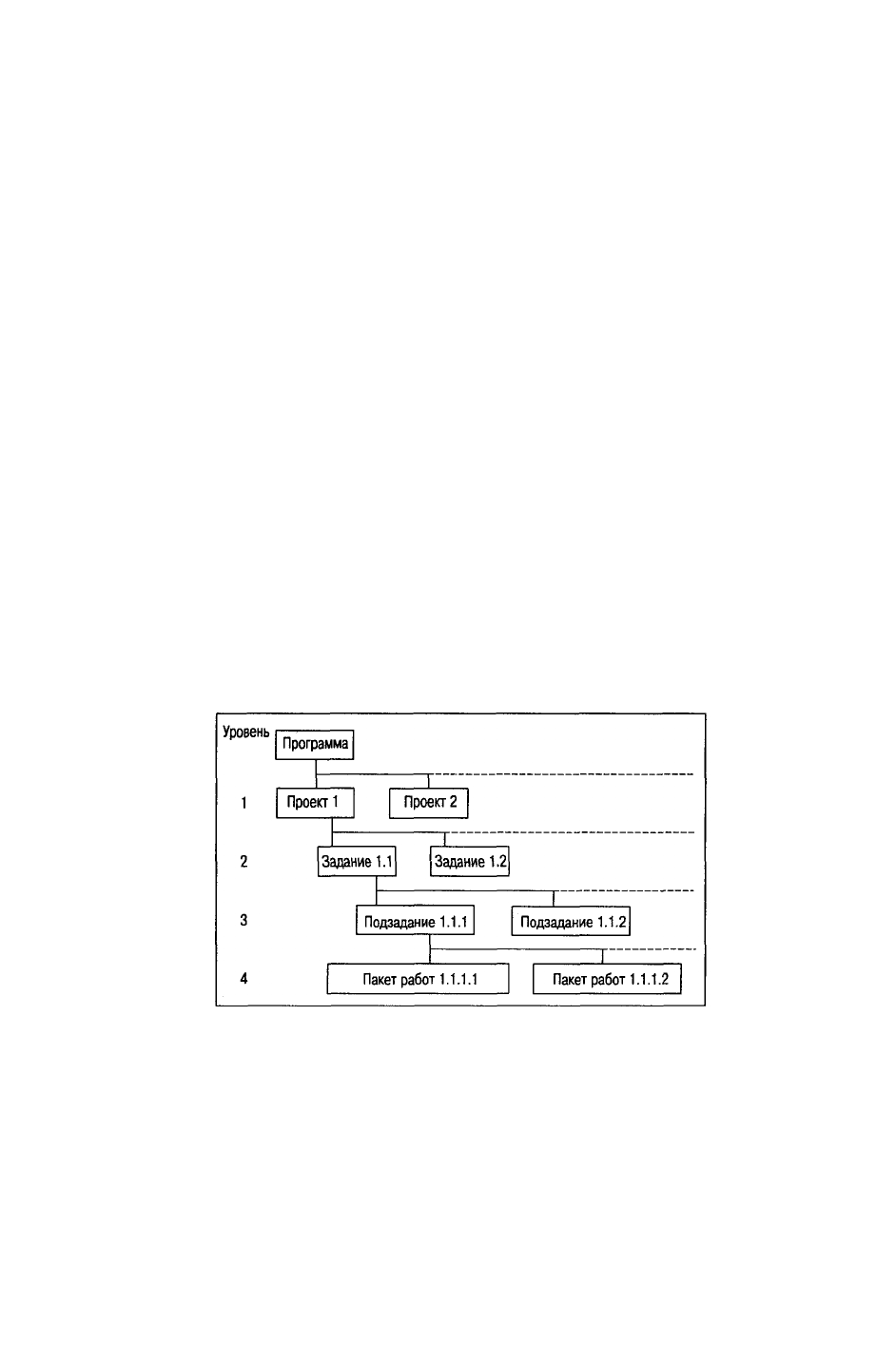
Структурой работ проекта (Work Breakdown Structure — WBDS) определяется иерархия

проектных заданий, подза-даний и пакетов работ. Выполнение одного или нескольких подзаданий

приводит к выполнению задания; выполнение всех заданий знаменует завершение проекта.

Данная структура наглядно отображена на приведенной ниже схеме.

В табл. 3.1 приведен пример структуры работ конкретного проекта — конструкторской

разработки оптического сканирующего устройства.

Обратите внимание, насколько удобно распределение операций по нумерованным уровням.

Например, "Проектирование телескопического устройства" (третий пункт сверху) обозначен

номером 1.1.1 (первый элемент уровня 1, первый элемент уровня 2 и первый элемент уровня 3). А

операция "Регистрация данных..." (13-й пункт сверху) пронумерована как 1.2.4.

Если вы хотите правильно разработать структуру работ проекта, рекомендуем выполнять

следующие советы.

■ Стремитесь к тому, чтобы над выполнением каждого элемента структуры можно было

работать независимо от других.

■ Следите за тем, чтобы размеры элементов структуры позволяли эффективно ими управлять.

■ Четко распределите полномочия, связанные с выполнением каждого элемента проекта.

■ Следите за ходом выполнения проекта.

■ Обеспечивайте все необходимые ресурсы.

Контроль за ходом выполнения проекта

Механизмы отчетности

Министерство обороны США, которое одним из первых применило в своей работе

рассматриваемый принцип управления проектами, в свое время разработало множество весьма

удобных стандартных форм для контроля хода работ. Многие из них в исходном либо

модифицированном виде широко использовались фирмами, занимающимися управлением

проектами. Однако с тех давних пор было создано большое количество графических

компьютерных программ, благодаря которым руководство компаний, заказчики и менеджеры

проектов получили возможность выбирать самые разнообразные варианты представления

процесса контроля за ходом проекта.

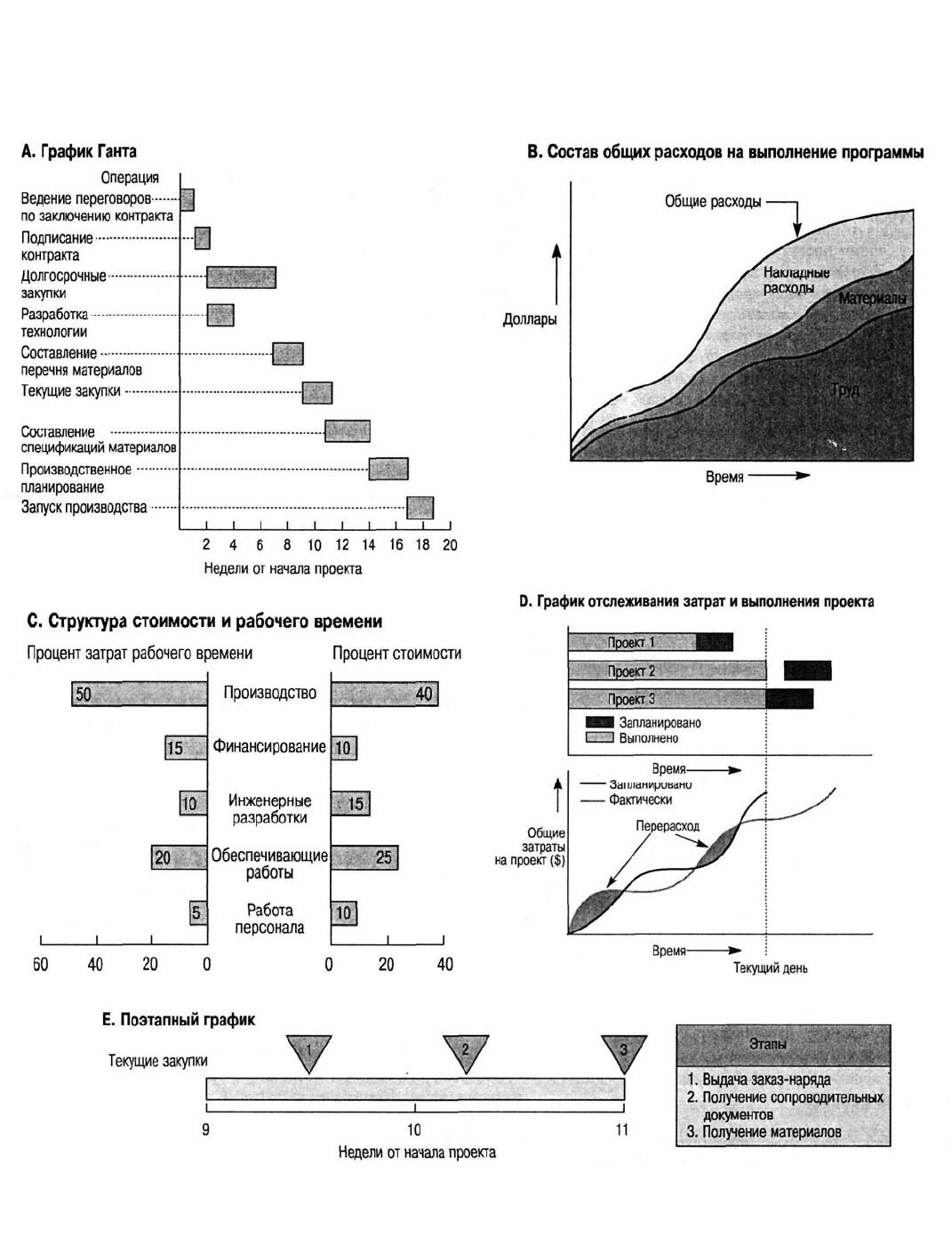
Взгляните на рис. 3.1.

На рис. 3.1 (фрагмент А) вы видите пример графика Ганта (Gantt Chart), на котором

отображается время начала и окончания каждой операции проекта и последовательность, в

которой все эти операции выполняются. Так, например, "Долгосрочные закупки" и "Разработка

технологии" — это операции, которые не зависят друг от друга и могут выполняться

одновременно. Все же остальные операции должны следовать строго одна за другой, в порядке,

указанном на графике.

График В на рис. 3.1 отображает затраты, распределенные во времени нарастающим итогом, на

труд, материалы, а также накладные расходы. Из такого отчета видны направления и размеры

затрат в ходе выполнения проекта.

Диаграмма С на рис. 3.1 показывает, какой процент всего рабочего времени проекта

затрачивается по различным видам деятельности: производство, финансирование и т.д.

Трудоемкость и затраты по отдельным видам указываются относительно общей трудоемкости и

стоимости проекта. Так, например, из диаграммы видно, что на производство выделено 50%

рабочего времени всего проекта, однако эти 50% занимают только 40% общей стоимости.

В верхней части отчета D на рис. 3.1 отображена степень выполнения трех проектов.

Штриховой вертикальной линией обозначен текущий день. Из диаграммы видно, что Проект 1

реализуется с опозданием, поскольку работа, которая должна быть на этот день закончена, еще не

выполнена. Проект 2 временно приостановлен, поэтому между выполненной и запланированной

частями работы есть пробел. Работа над Проектом 3 продолжается без остановки. В нижней части

этого же рисунка графически сравниваются фактические и плановые общие затраты по проекту.

Как видно из графика, дважды наблюдался перерасход средств, однако текущие суммарные

издержки не выходят за пределы установленного лимита.

Поэтапный график Е на рис. 3.1 имеет три отметки окончания этапов, обозначающих

конкретные события в процессе реализации проекта. В соответствующие моменты времени

проводится проверка, позволяющая определить, нет ли опоздания с выполнением какой-либо

операции. В данном примере такими операциями являются "Выдача заказ-наряда" на поставку

материалов, "Получение сопроводительных документов" и "Получение материалов".

Для более подробного предоставления данных можно использовать также другие стандартные

отчеты: отчет, в котором фактические затраты сравниваются со степенью завершенности проекта,

например таблица состояния затрат (Cost Schedule Status Report — CSSR), или отчеты по учету

частичных платежей, например отчет о накопленной стоимости.

Таблица 3.1. Структура работ проекта разработки большого оптического сканера

Уровни

1 2 3 4

1. Проектирование оптического моделирующего устройства

1.1. Проектирование оптики

1.1.1 Проектирование телескопического устройства

1.1.2 Разработка оптического интерфейса телескоп/моделирующее устройство

1.1.3 Проектирование моделирующего устройства трансфокаторной системы

1.1.4 Разработка спецификаций компонентов оптического моделирующего устройства

1.2 Анализ эффективности системы

1.2.1 Проверка работы общей системы программного и микропрограммного обеспечения

х 1.2.1.1 Разработка и анализ логической блок-схемы

х 1.2.1.2 Разработка базового алгоритма управления

1.2.2 Тестирование действия дальнего луча

1.2.3 Разработка метода внутренней и внешней коррекции системы

1.2.4 Регистрация данных и выработка требований к сокращению изображения

1.3 Интеграция системы

1.4 Анализ затрат

1.4.1. Анализ структуры соотношения затраты/ система

1.4.2 Анализ эффективности соотношения затраты/система

1.5 Менеджмент

1.5.1 Управление конструкторским и инженерным процессом

1.5.2 Управление программой

1.6 Закупки компонентов

1.6.1 Оптика

1.6.2 Сигнальные компоненты

1.6.3 Детекторы

Организационные структуры

Прежде чем приступить к реализации проекта, высший управленческий персонал должен

решить, какая из трех организационных структур будет использоваться для привязки данного

проекта к организационной структуре фирмы: обособленный, матричный или функциональный

проект. Если, например, выбирается матричная форма, то разные проекты (строки матриц)

заимствуют ресурсы из разных функциональных зон (столбцов). Далее руководителям следует

принять решение, какая именно матрица будет использоваться: слабая, сбалансированная или

жесткая. Таким образом определяется, какой степенью полномочий будут наделены менеджеры

проекта по отношению к функциональным менеджерам, с которыми они совместно принимают

решения. Высшее руководство фирмы должно также внимательно ознакомиться с персональной

характеристикой будущего руководителя проекта. (Врезка "Как выбрать хорошего руководителя

проекта".) Дальше мы подробнее обсудим преимущества и недостатки всех трех упомянутых

выше форм организационных структур проекта.

Обособленный проект

Том Питерс (Tom Peters) предсказывает, что "в ближайшем будущем подавляющая часть

работы, выполняемой в мире, будет иметь отношение к умственному труду, которым на

полупостоянной основе будут заниматься небольшие группы специалистов, нацеленные на

реализацию конкретных проектов. Каждая такая группа станет своего рода автономным

предпринимательским центром с определенными возможностями. Постоянное стремление к

высокой скорости работы и гибкости в таких группах непременно приведет к полному вымиранию

иерархических управленческих структур, на которых воспитывались наши предки и мы"

. Таким

образом, из трех основных организационных структур, по мнению г-на Питерса, наиболее

жизнеспособен так называемый обособленный проект (Pure Project), основной характеристикой

которого является то, что над конкретным проектом постоянно работает самостоятельная группа

специалистов.

Рис. 3.1. Примеры графического представления отчетов о ходе выполнения проекта

Tom Peters, Liberation Management (New York: Alfred A. Knopf, 1992), p. 5 и форзац обложки.

Как выбрать хорошего руководителя проекта

В процессе поиска, отбора, найма и ПОДГОТОВКИ людей, которые будут управлять реализацией

того или иного проекта, руководство компании должно проявлять трезвый расчет и инициативу. В

компании Toyota, например, менеджеры высшего уровня всегда выбирают руководителя проекта,

чьи личные качества соответствуют виду продукции, которую они собираются осваивать. Так,

когда речь шла о спортивных автомобилях, рассчитанных на молодого и агрессивного

потребителя, они искали человека именно такого типа. Когда же проект посвящался разработке

роскошного седана, был выбран серьезный и респектабельный человек. В общем говоря, задача

состоит в том, чтобы выбрать руководителя проекта, который, отождествляя себя и с проектом, и с

будущими потребителями, мог бы самостоятельно, без посторонней помощи, учитывать все

требования относительно общих характеристик и критериев системы.

Источник. Steven С. Wheelwright and Kim В. Clark, Leading Product Development (New York: The

Free Press, 1995), p. 91.

Преимущества

• Менеджер проекта получает все полномочия, связанные с его реализацией.

• Члены группы отчитываются перед одним руководителем. Им не приходится беспокоиться

о проявлении преданности и верности функциональному менеджеру.

• Процедура обмена мнениями значительно сокращается, в результате чего решения

принимаются намного быстрее.

Такие понятия, как командная гордость, мотивация и преданность делу, приобретают очень

большое значение. Недостатки

• Дублирование ресурсов. Оборудование и персонал не используются в разных проектах.

• Игнорируются организационные цели и политика предприятия, поскольку члены групп

часто как психологически, так и физически перемещаются из одного подразделения в другое.

• Вследствие ослабления связи функциональных подразделений организация запаздывает с

освоением новых технологий.

• Поскольку члены групп не имеют "родной" функциональной зоны, их беспокоит, что они

будут делать после завершения проекта, что нередко приводит к затягиванию сроков его

выполнения.

Функциональный проект

Полной противоположностью предыдущей организационной структуре является

функциональный проект (Functional Project). Он характеризуется тем, что проект

осуществляется в существующих функциональных подразделениях.

Преимущества

• Члены проектной группы могут одновременно работать над несколькими проектами.

Технический опыт сохраняется в пределах конкретной функциональной зоны, даже если

участник проекта покидает группу или увольняется из организации.

Функциональная зона остается "родной" для участников проектной группы даже после

реализации проекта. Функциональные специалисты могут продвигаться вверх по службе.

Вследствие насыщенности группы высокопрофессиональными специалистами из нескольких

функциональных зон повышается эффективность решения различных технических проблем,

связанных с проектом.

Недостатки

Аспектам проекта, не связанным непосредственно с конкретной функциональной зоной,

уделяется недостаточно внимания.

Мотивация командной работы часто очень слаба.

Потребности клиента носят вторичный характер, и реакция на них замедлена.

Матричный проект

Классическая матричная организационная форма характеризуется тем, что в ней

объединяются качества структур как обособленного, так и функционального проектов. В каждом

таком проекте задействованы люди из разных функциональных зон. Менеджер проекта (Project

Manager — РМ) принимает решения относительно того, какие задания и когда должны

выполняться, а функциональные менеджеры решают, какие именно люди будут заниматься этой

работой и какие технологические приемы следует применять.

Преимущества

• Усиливается взаимосвязь между различными функциональными подразделениями.

• Менеджер проекта несет ответственность за его успешную реализацию.

• Дублирование ресурсов сводится к минимуму.

• Функциональная зона остается "родной" для членов проектной группы даже после

завершения проекта, поэтому они менее обеспокоены своей судьбой после его окончания, чем при

такой организационной структуре, как обособленный проект.

• Деятельность по реализации проекта согласуется с политикой основной организации, что

усиливает поддержку проекта.

Недостатки

• Появляются два руководителя, и зачастую мнение функционального менеджера

выслушивается прежде, чем мнение менеджера проекта. При такой ситуации, кроме всего прочего,

трудно сказать, кто из них важнее для продвижения конкретного человека по службе.

• Проект обречен на неудачу, если менеджер проекта лишен таланта успешно вести

переговоры.

• Определенную опасность таит в себе то, что менеджеры проектов стремятся иметь запас

ресурсов для своих проектов, нанося тем самым вред другим программам компании.

Обратите внимание, что, независимо от того, какая именно из трех организационных структур

выбрана, непосредственный контакт с заказчиком осуществляется через менеджера проекта.

Следует помнить, что взаимодействие и скорость реакции на запросы потребителя резко

повышаются, если за успех проекта отвечает один человек.

Сетевой график

Понятие сетевого графика относится к набору графических методов, используемых при

планировании хода проекта и наблюдении за ним. Для любого типа проекта основными

факторами являются время, затраты

(издержки) и наличие ресурсов. Сетевые методы были разработаны для планирования и

отслеживания всех этих факторов как по отдельности, так и в различных комбинациях. Далее в

этой главе вашему вниманию предлагается краткий обзор истории развития терминологии, а

также подробное описание временных моделей, моделей типа "время—затраты" и моделей

управления ограниченными ресурсами.

Наиболее известными методами составления сетевого графика являются PERT (Program

Evaluation And Review Technique — метод оценки и пересмотра программ) и СРМ (Critical Path

Method — метод критического пути). Оба они разработаны в 50-х годах. Метод PERT был создан

в 1958 году под эгидой Управления специальных проектов ВМС США (U.S. Navy Special Projects

Office) как инструмент для составления графика и контроля за ходом работ при разработке ракет

Polaris. СРМ является детищем ученых Дж. И. Келли (J. Е. Kelly, компания Remington-Rand) и М.

Р. Уокера (М. R. Walker, компания Du Pont), его создание относится к 1957 году. Данный метод

изначально использовался как вспомогательный инструмент, применяемый при составлении

графиков проведения технического обслуживания на химических заводах.

В компании Boeing методы эффективного управления проектами играли чрезвычайно важную

роль как в процессе разработки сборочно-монтажной схемы 777, так и при календарном

планировании работ и в производственном процессе. Заметим, что 20% самолетов модели 777

строятся в Японии, а комплектующие поставляются другими странами: Австралией (рулевое

управление), Северной Ирландией и Сингапуром (передние опоры шасси), Кореей (законцовки

крыла), Бразилией (здесь проводится сборка законцовок крыла и хвостового оперения) и Италией

(внешние закрылки).

Используя упомянутые выше методы, проект легко представить в графической форме, и его

отдельные задания связываются между собой таким образом, чтобы основное внимание было

сосредоточено на важнейших для выполнения проекта моментах. Чтобы методы составления

графика критического пути можно было применить с наибольшей эффективностью, проект

должен обладать следующими характеристиками.

1. В нем должны быть точно определены операции или задания, которые обозначают начало и

окончание проекта.

2. Задания или операции должны быть взаимно независимы. Необходимо, чтобы в пределах

определенной последовательности их можно было начинать, приостанавливать, исключать и

выполнять независимо один от другого.

3. Необходимо наметить точный порядок выполнения операций и заданий; они должны

выполняться в определенной последовательности.

Перечисленные выше свойства проектов характерны для таких отраслей промышленности, как

строительство, самолетостроение и судостроение, поэтому методы сетевых графиков

применяются в них особенно широко. Кроме того, как мы уже упоминали, эти методы и другие

принципы управления проектами все чаще используются фирмами, которые работают в отраслях

промышленности, имеющих тенденцию быстро меняться.

Временные модели

В своих базовых формах методы PERT и СРМ предназначены для определения наиболее

длительного по времени пути в цепи работ, который становится основой при планировании и

контроле за ходом выполнения проекта. Для графического отображения этой последовательности

в обоих методах применяются линии со стрелками и узлы. Изначально PERT и СРМ отличались

между собой тем, что в сетевом графике PERT операция обозначалась стрелкой, а в СРМ — узлом

(кружком). Существовало и еще одно различие: в PERT использовались три типа оценки

продолжительности операций (оптимистическая, пессимистическая и наиболее вероятная), а в

СРМ — только наилучшая. Эти различия объясняются тем, что метод PERT разрабатывался для

работы со сложными проектами, которые характеризуются высокой степенью неопределенности, а

СРМ — для составления графиков рутинных операций, связанных с заводским техническим

обслуживанием. За долгие годы существования этих двух методов различия между ними стерлись,

поскольку пользователи СРМ начали также применять три оценки продолжительности операций, а

в сетевых графиках PERT операции нередко обозначаются узлами.

По нашему мнению, если операция обозначается узлом, то работать с графиком намного

удобнее. Три оценки продолжительности операций позволяют использовать их для определения

вероятностных характеристик сроков их выполнения. Итак, в этой книге мы будем обозначать

операцию узлом, а для оценки продолжительности операций использовать либо одну оценку, либо

три, в зависимости от назначения графика. Кроме того, хотим обратить ваше внимание, что

термины PERT и СРМ в нашем тексте взаимозаменяемы и применяются для обозначения одних и

тех же понятий, хотя мы предпочитаем пользоваться вторым термином.

По сути, оба эти метода обязаны своим появлением их широко известному предшественнику,

графику Ганга. График Ганта позволяет привязать операции ко времени. Однако в проектах с

числом операций 25—30, график оказывается слишком громоздким для визуального восприятия.

Кроме того, график Ганта не располагает прямой процедурой для определения критического пути,

но, несмотря на ряд таких недостатков, он имеет огромное практическое значение.

Сетевой график с однозначной оценкой продолжительности операций

Предлагаем вашему вниманию простой пример составления сетевого графика проекта.

Обратите внимание, что продолжительность каждой операции в данном случае указывается с

использованием однозначной, т.е. наиболее вероятной, оценки (а не трех оценок, которые мы

обсудим позднее в этой главе).

Пример 3.1. Однозначная оценка продолжительности операций

Известно, что многие фирмы, предпринявшие попытку выйти на рынок сбыта компьютеров

типа "ноутбук", потерпели фиаско. Теперь представьте, что ваша компания решила, что на рынке

существует большой спрос на эту продукцию. Такое решение было основано на том, что

большинство предлагаемых моделей портативных компьютеров характеризуются плохой

конструкцией: компьютеры либо слишком велики и тяжелы, либо чрезмерно малы для того, чтобы

пользоваться при работе на них стандартной клавиатурой. Ваша же модель будет настолько мала,

что при желании ее можно будет носить в кармане пиджака (оптимальный размер— не больше 12

ч 24 ч 2,5 см) и иметь складную клавиатуру. Она будет весить до 0,5 кг, оснащена на жидких

кристаллах дисплеем, микродисководом и портом для работы в глобальных сетях. Продукция

предназначена для бизнесменов, однако может применяться и более широким кругом

потребителей, например студентами, поэтому цена на нее не должна превышать 175-200 долларов.

Таким образом, в задачи проекта входит конструирование, разработка и создание опытного

образца такого компьютера. В быстро меняющейся отрасли производства компьютерной техники

чрезвычайно важно освоить новую модель и вывести ее на рынок не позже, чем через год.

Следовательно, ваша проектная группа имеет в своем распоряжении около восьми месяцев (35

недель).

Решение

Первым делом проектная группа должна составить сетевой график проекта (Project Network

Chart) и определить степень вероятности создания опытного образца компьютера за 35 недель.

Давайте проследим этапы составления такого графика.

1. Идентификация операций. Проектная группа приходит к выводу, что узловыми событиями

проекта должны стать следующие операции: конструирование компьютера, изготовление

опытного образца (прототипа), его тестирование, разработка технологии изготовления, подбор,

приобретение и монтаж оборудования и составление итогового отчета, обобщающего все аспекты

конструирования, технологии и производства.

2. Определение последовательности операций и построение сетевого графика. На основе

обсуждения, проведенного в группе, менеджер проекта составляет таблицу с перечнем работ с

указанием последовательности их выполнения и сетевой график, которые изображены на рис. 3.2.

На сетевом графике операции обозначены узлами, а стрелки указывают последовательность

выполнения операций.

При построении сетевого графика следует внимательно расположить операции в надлежащем

порядке, сохраняя при этом логическую взаимосвязь между ними. Так, например, ситуация, при

которой операция А предшествует операции В, операция В — операции С, а операция С —

операции А, была бы нелогичной.

3. Определение критического пути. Критическим путем называют цепочку последовательно

связанных операций в сетевом графике с наибольшей продолжительностью. Он характеризуется

как путь с нулевым резервом времени. Резерв времени поочередно вычисляется отдельно для

каждой операции. Он представляет собой разницу между поздним и ранним ожидаемыми сроками

завершения работ. Резерв также описывается как время, на которое можно задержать выполнение

отдельной операции, не увеличивая при этом срок окончания всего проекта. Для правильного

составления графика необходимо вычислить для каждой операции четыре временных параметра:

• ранний срок начала операции от начала проекта (Early Start Time — ES);

• ранний срок окончания операции от начала проекта (Early Finish Time — EF);

• поздний срок окончания операции (Late Finish Time— LF), т.е. крайний срок, когда операцию

можно завершить, не задерживая окончания всего проекта;

• поздний срок начала операции (Late Start Time — LS), т.е. поздний срок окончания, минус

время, необходимое для выполнения операции.

Процедуру вычисления этих показателей, определения резерва времени и критического пути

легче всего объяснить на простом сетевом графике, изображенном на рис. 3.3. Буквами

обозначены операции, а цифрами — их средняя продолжительность.

a) Определим срок ES. В качестве даты начала проекта принимается "нулевой" день, и он же

будет ранним сроком начала операции А. Чтобы получить ES для операции S, мы прибавляем

продолжительность операции А (т.е. 2) к 0 и получаем значение 2. Точно так же ES для операции

С будет 0 + 2 = 2. Чтобы вычислить ES для операции D, мы берем большее значение ES и

продолжительность времени для каждой из предшествующих операций. Поскольку путь через

операцию В = 2 + 5 = 7 больше пути через операцию С = 2 + 4 = 6, ES для D = 7. Эти значения

указываются в сетевом графике (см. рис. 3.3, этап а). Наибольшее значение выбирается потому,

что операцию D нельзя начать прежде, чем будет завершена самая продолжительная из

предшествующих ей операций.

b) Теперь вычислим срок EF. EF для операции А равен ее сроку ES (т.е. 0) плюс ее

продолжительность 2. EF операции В равен ее сроку ES (т.е. 2), плюс продолжительность 5, т.е. 7.

EF для операции С будет 2 + 4 = 6, а для операции D: 7 + 3 = 10 (см. рис. 3.3, этап о). На практике

ES и EF вычисляются вместе, по мере построения сетевого графика. Поскольку ES плюс время

продолжительности операции равняется EF, то EF предшествующей операции является ES для

следующей, и т.д.

c) Затем вычисляются поздние сроки начала и завершения операций (LF и LS). Процедуру этих

вычислений можно выразить в математической форме, однако, с нашей точки зрения, ее проще

объяснить и освоить, представив ее на чисто понятийном уровне. Расчет LS и LF начинают с

конца проекта, т.е. с какого-то определенного предполагаемого или желательного срока его

завершения. Двигаясь потом от конца к началу и анализируя все операции по очереди, мы

определим, насколько можно задержать начало каждой операции, не задерживая при этом начала

следующей за ней операции. Если говорить конкретно о сетевом графике, изображенном на рис.

3.3 (этап с), то вначале предположим, что поздний срок завершения проекта совпадает с ранним

сроком окончания операции D, т.е. равен 10. В таком случае поздний срок начала операции D

будет 10-3 = 7. Самый поздний срок, когда может быть выполнена операция С, не задерживая LS

для D, равен 7, что означает, что LS для операции С будет 7-4, т.е. 3. Наиболее поздний срок, когда

можно завершить операцию В, не задерживая LS операции D, также равен 7, что означает, что LS

для операции В составляет 7-5 = 2. Поскольку операция А предшествует двум операциям, выбор

значений LS и LF зависит от того, какая из этих операций должна начинаться первой. Очевидно,

что в данном примере показатель LF для операции А должен определяться на основе операции S,

поскольку ее значение LS равно 2, в то время как выполнение операции С можно отложить только

на один день, в противном случае это повлечет за собой задержку окончания проекта. И наконец,