Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

няется на величину, пропорциональную С

. Зная значе-

ние одного из корней уравнения (II.7), можно понизить

его степень. При этом 'получаем

+ / (lЩЩгС-±2г*е»-Щ^0. (11.12)

Если затухание в линии пренебрежимо мало (а?=0),

то (11.12) может быть сведено к уравнению с веществен-

ными коэффициентами. Зависимости вещественной и

1,0

0,9

0,8

0,7

0,5

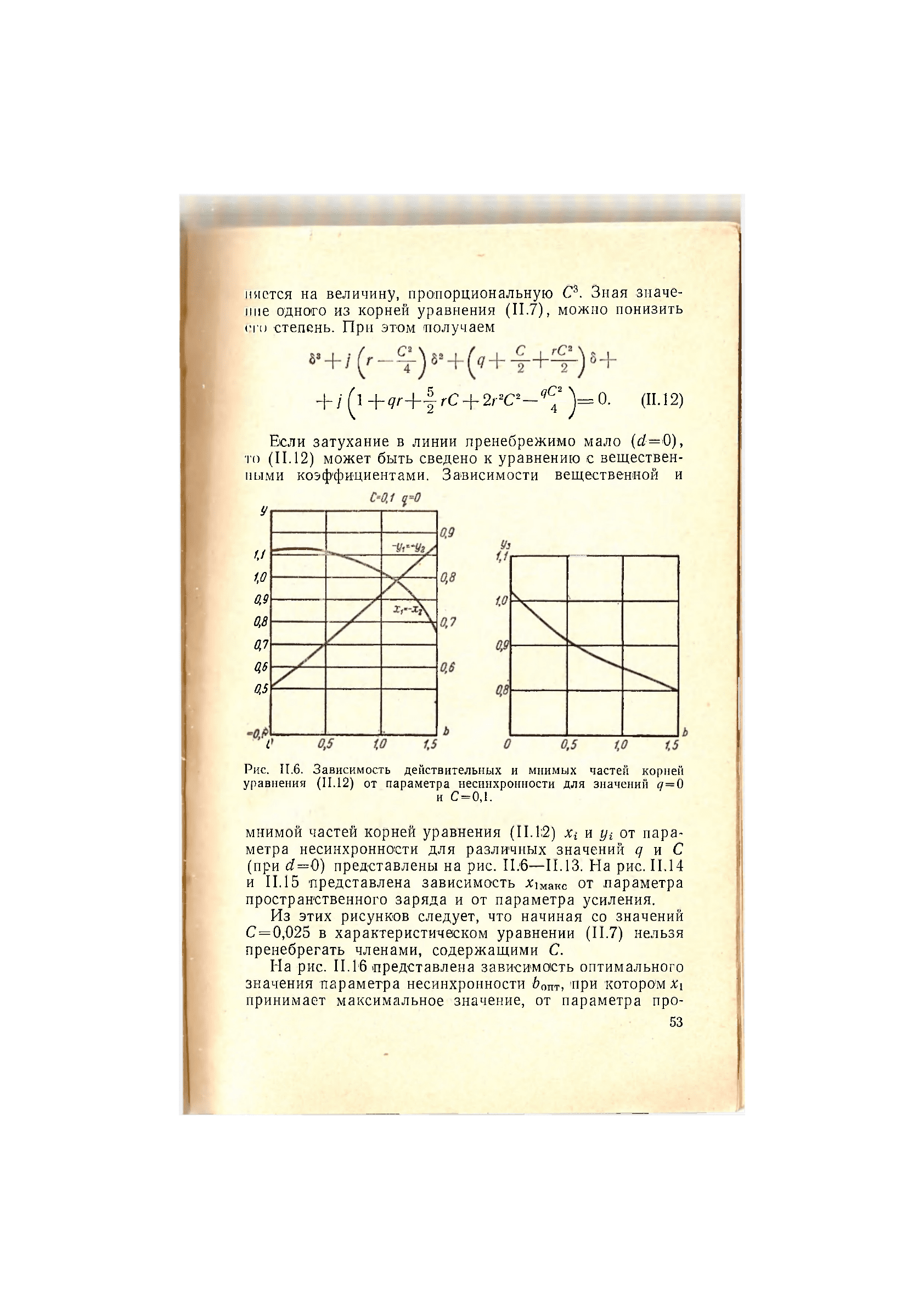
Рис. II.6. Зависимость действительных и мнимых частей корней

уравнения (11.12) от параметра несинхронности для значений q=О

и С=0,1.

мнимой частей корней уравнения (11.12) Х{ и щ от пара-

метра несинхронности для различных значений q и С

(при d=0) представлены на рис. И.6—11.13. На рис. 11.14

и 11.15 'представлена зависимость ломаке от параметра

пространственного заряда и от параметра усиления.

Из этих рисунков следует, что начиная со значений

С=0,025 в характеристическом уравнении (II.Т) нельзя

пренебрегать членами, содержащими С.

На рис. 11.16 представлена зависимость оптимального

значения параметра несинхронности й

0П

т, 'при котором х\

принимает максимальное значение, от параметра про-

странсгвённого заряда. Полученные результаты расчета

постоянных распространения при больших значениях

параметра усиления С отличаются от приведенных в ра-

ботах (3, 4]. Это объясняется тем, что данные в [3, 4]

получены из ошибочного характеристического уравне-

ния [1]. На рис. 11.14 пунктирными кривыми показана

зависимость Хщакс от q, приведенная в [3].

2.0 2.5

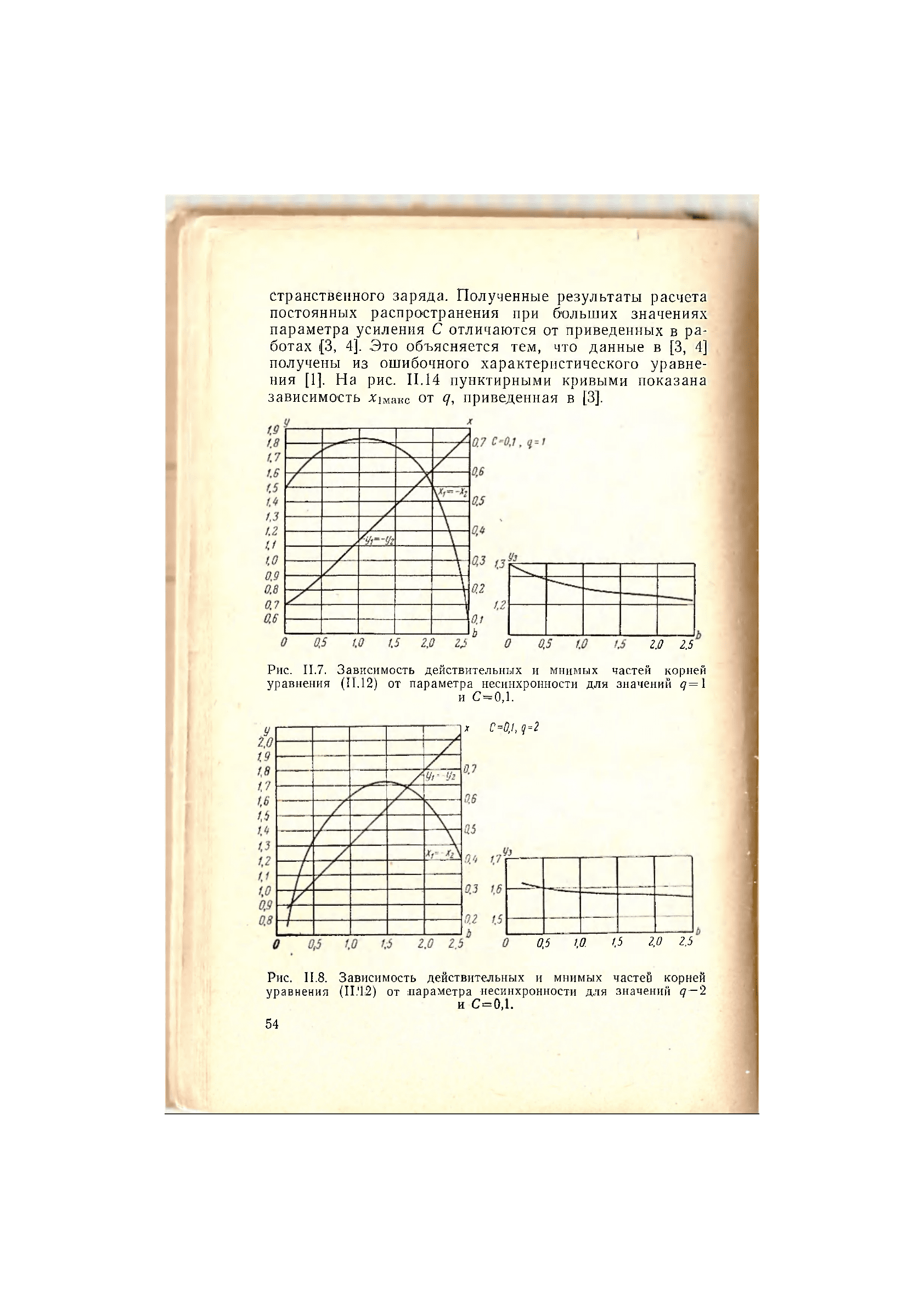
Рис. II.7. Зависимость действительных и мнимых частей корней

уравнения (11.12) от параметра несинхронности для значений q=

и С=0,1.

С=0,1, (j=2

0,5 1.0 1.5 2.0 2.5

Рис. II.8. Зависимость действительных и мнимых частей корней

уравнения (II.'12) от параметра •несинхронности для значений q—2

и С=0,1.

При построении пунктирных кривых использовано

соотношение, связывающее ^параметр q с параметром

пространственного заряда 4QC, введенным в [1]:

4 QC

\\—сущсу

Сравнение этих кривых показывает, что расчет по

графикам [3] дает завышенные значения усиления. Зави-

симость л:

акс от параметра усиления для различных

C=0,hq=3

1,9

1,8

Уз

1.0 1,5 2,0 2.5

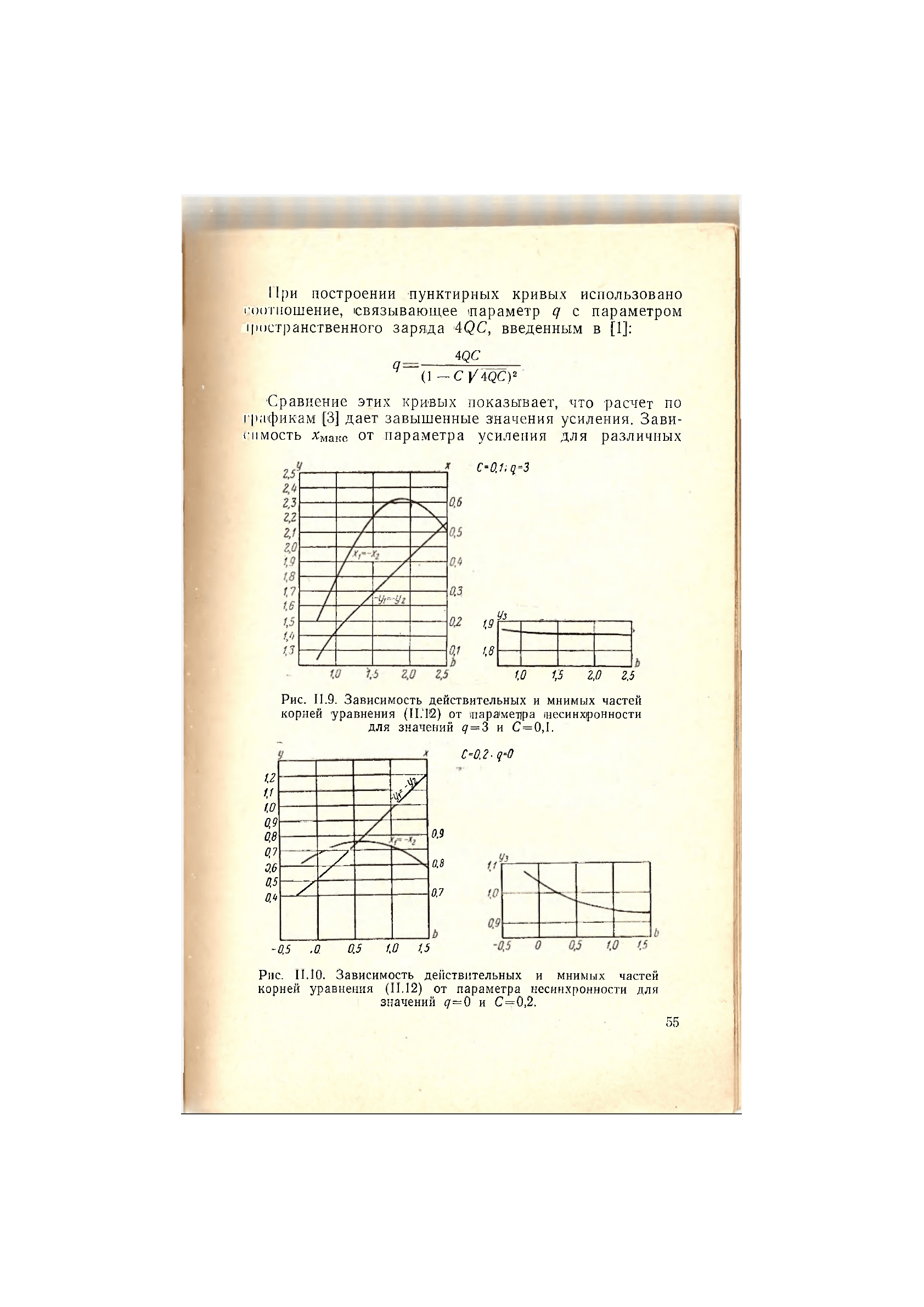
Рис. 11.9. Зависимость действительных и мнимых частей

корней уравнения (И.'1!2) от лара'мецра гаесинхронности

для значений <7=3 и С=0,1.

С-0.2*

д-0

1,2

1,0

0,9

0,8

0,7

0,6

0,5

0,<*

ш ш

' /

0,9

0.8

0.7

-0.5 .0 0.5 1,0 1,5

Рис. 11.10. Зависимость действительных и мнимых частей

корней уравнения (11.12) от параметра несинхронности для

значений q=0 и C=f0,2.

значений 4QC, приведенная в [3], показывает, что с ро-

стом пространственного заряда усиление, -приходящееся

на длину 'волны в электронном пучке, увеличивается.

Обычно при анализе взаимодействия электронного

потока с бегущей электромагнитной волной вводят

С*02: Ц-1

0,8

0,7

0.6

У}

0,5

1.3-

0 0.5 10 1,5 2.0 2,5

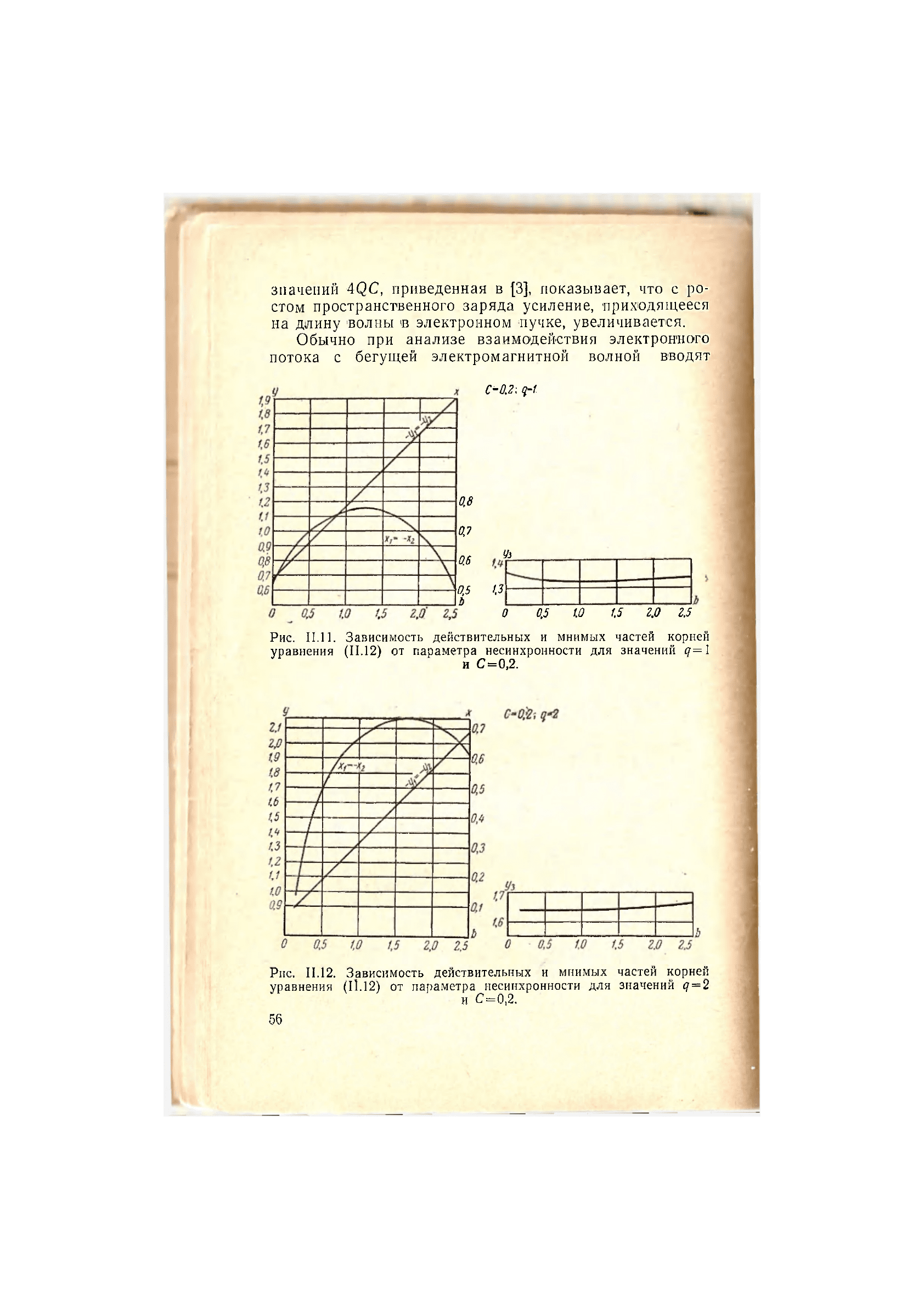
Рис. 11.11. Зависимость действительных и мнимых частей корней

уравнения (11.12) от параметра несинхронности для значений q=\

и С=0,2.

Рис. 11.12. Зависимость действительных и мнимых частей корней

уравнения (11.12) от параметра несинхронности для значений q=2

и С=0,2.

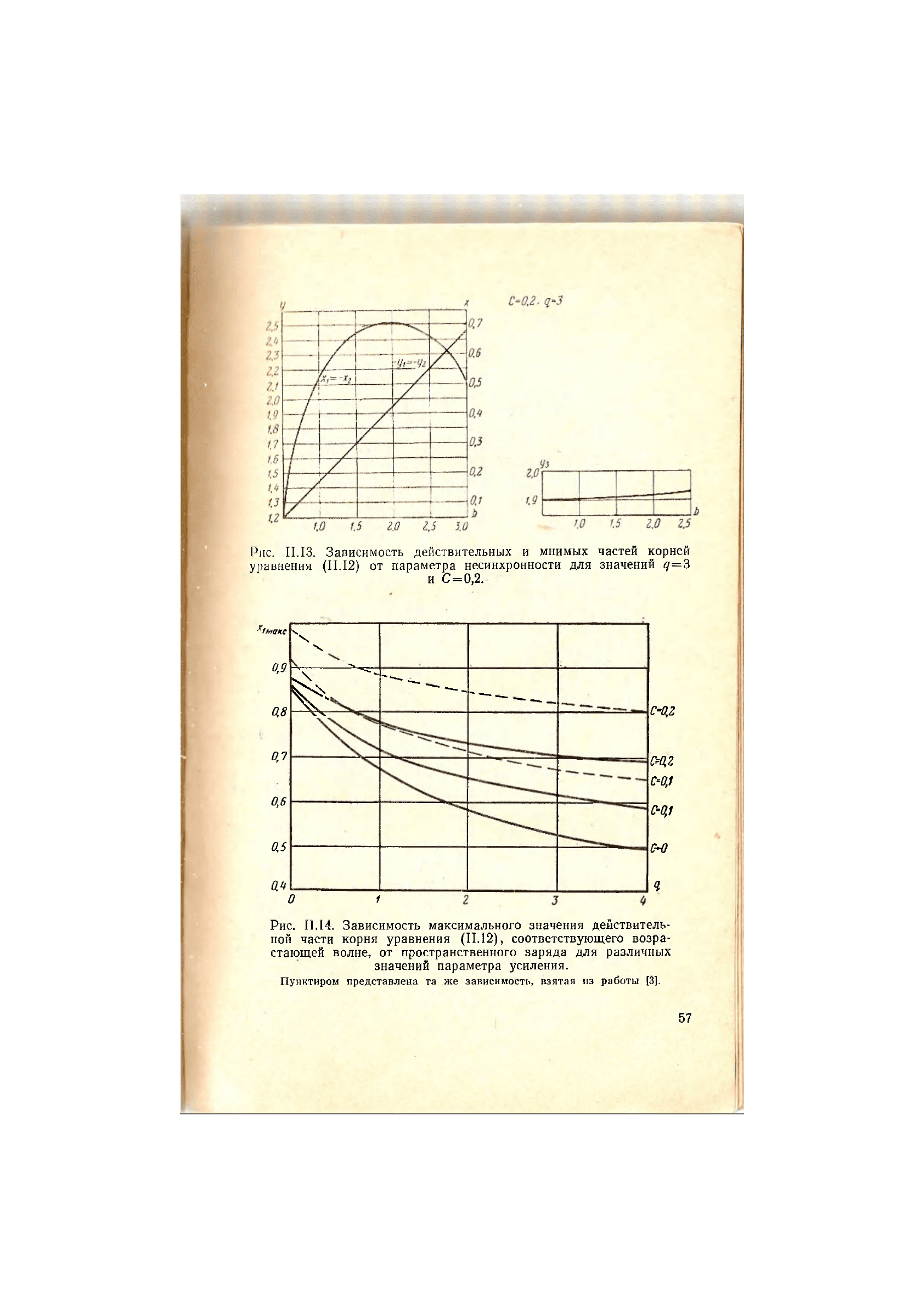
Рис. 11.13. Зависимость действительных и мнимых частей корней

уравнения (11.12) от параметра несинхронности для значений <7=3

и С=0,2.

х,

/маке

0,9.

0,7

0,6

0,5

0.4

Щк '

|Щ^й—

- — — —

С-0,2

00,2

С-0,1

00,1

V+0

Рис. 11.14. Зависимость максимального значения действитель-

ной части корня уравнения (11.12), соответствующего возра-

стающей волне, от пространственного заряда для различных

значений параметра усиления.

Пунктиром представлена та же зависимость, взятая из работы [3].

Рис. 11.15. Зависимость максимального значе-

ния действительной части корня уравнения

(11.12), соответствующего возрастающей волне,

от параметра усиления для различных значе-

ний параметра пространственного заряда.

Ат

Рис. 11.16. Зависимость оптимального значения параметра не-

сияхронности от пространственного заряда для различных

значений параметра усиления.

Пунктиром представлена зависимость b ~vq .

параметры b, q и d, которые удобны для расчета при

Малых значениях С. Так как они зависят от параметра

усиления, то они оказываются неудобными для анализа

работы ЛБВ при больших значениях С. Более удобными

являются параметры, не зависящие от С. В качестве

системы таких параметров могут быть введены сле-

дующие:

параметр пространственного заряда

параметр несинхронности

параметр затухания

где

— затухание в децибелах.

Эти параметры дают возможность наглядно предста-

вить зависимость усиления и оптимального значения

параметра несинхронности от пространственного заряда,

затухания и параметра усиления. На рис. 11.17 и 11.18

Рис. 11.17. Зависимость макс от параметра

СОд

—• для значений С = 0,1 и 0,2.

Va*

0,1

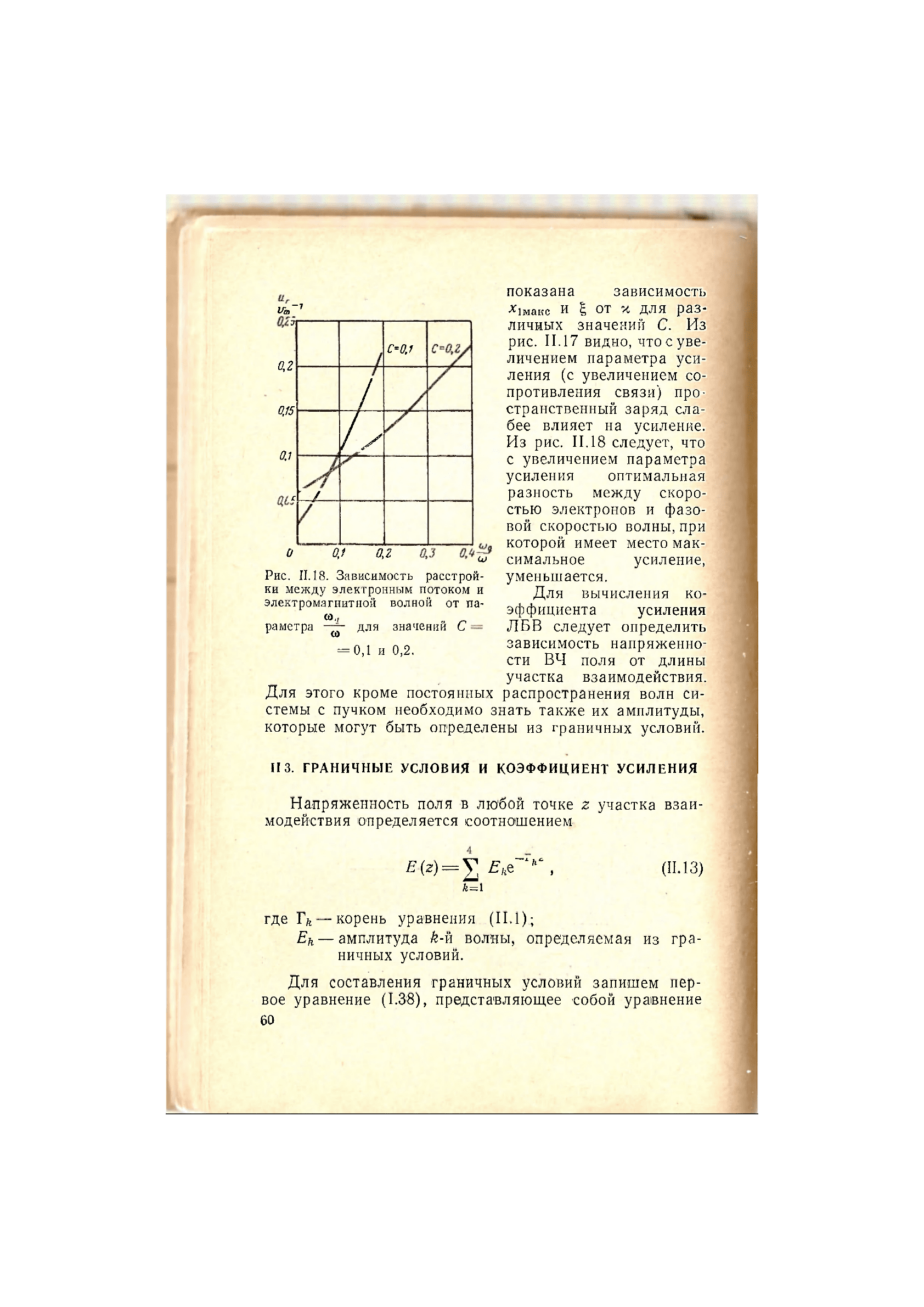
показана зависимость

*1макс И £ от Щ для раз-

личных значений С. Из

рис. 11.17 видно, что с уве-

личением параметра уси-

ления (с увеличением со-

противления связи) про-

странственный заряд сла-

бее влияет на усиление.

Из рис. 11.18 следует, что

с увеличением параметра

усиления оптимальная

разность между скоро-

стью электронов и фазо-

вой скоростью волны, при

которой имеет место мак-

симальное усиление,

уменьшается.

Для вычисления ко-

эффициента усиления

ЛБВ следует определить

зависимость напряженно-

сти ВЧ поля от длины

участка взаимодействия.

Для этого кроме постоянных распространения волн си-

стемы с пучком необходимо знать также их амплитуды,

которые могут быть определены из граничных условий.

С-0,1

f /

1 о

си

Рис. 11.18. Зависимость расстрой-

ки между электронным потоком и

электромагнитной волной от па-

со,

ра метра

со

для значений С

= 0,1 и 0,2.

ИЗ. ГРАНИЧНЫЕ УСЛОВИЯ И КОЭФФИЦИЕНТ УСИЛЕНИЯ

Напряженность поля в лю'бой точке z участка взаи-

модействия определяется соотношением:

{г) = 2 ,

k=\

(11.13)

где Tk — корень уравнения

(11.1).;

Ek — амплитуда &-й волны, определяемая из гра-

ничных условий.

Для составления граничных условий запишем пер-

вое уравнение (1.38), представляющее собой уравнение

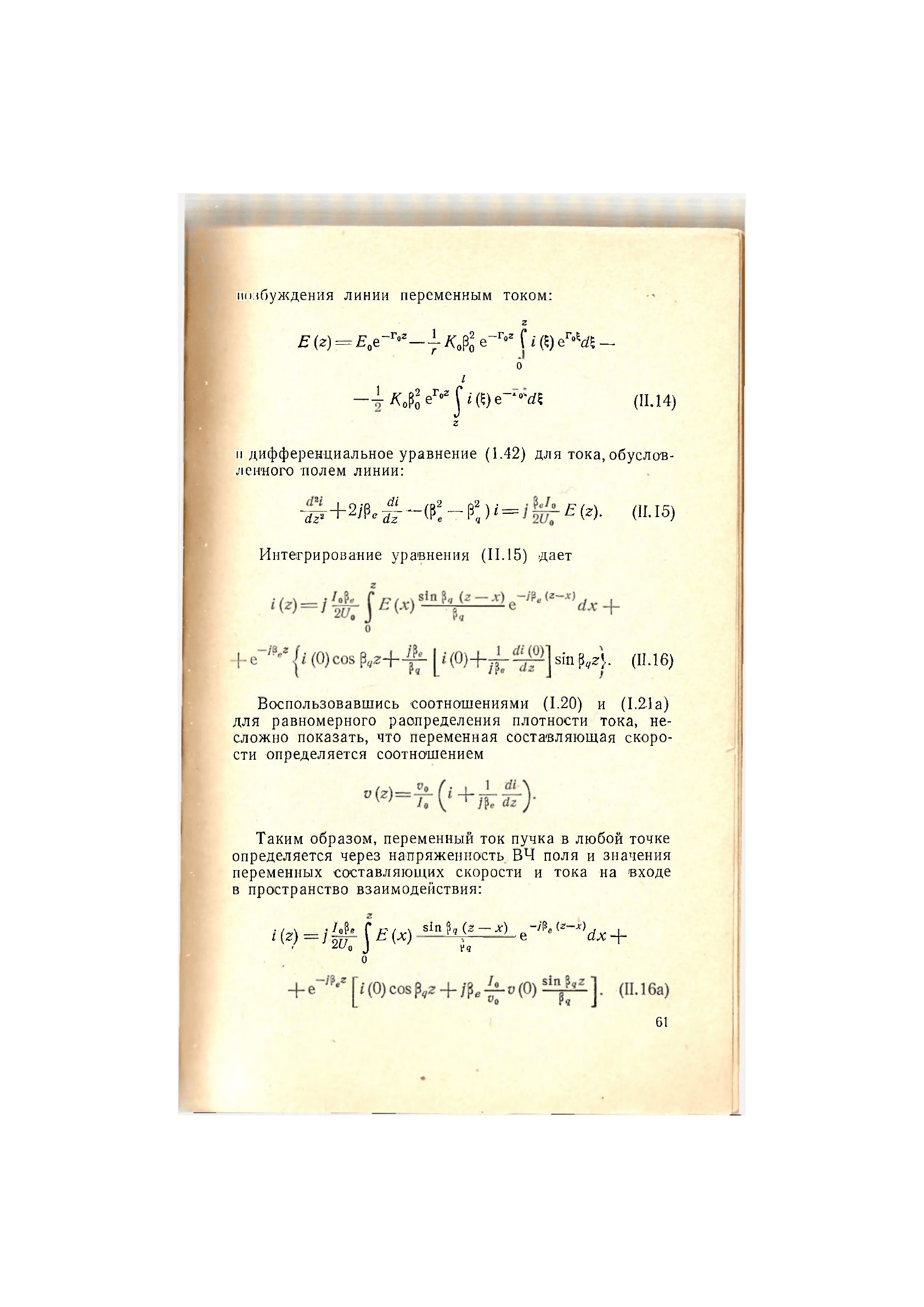
нозбуждения линии переменным током:

Е (г) р £

е~

-1 K

f i

(?)

еЧй -

—I Kf

Гог

J i (Е) (11.14)

и дифференциальное уравнение (1.42) для тока, обуслов-

ленного полем линии:

•щШЩШ - £ м-£ Ife

(II.

15)

Интегрирование уравнения (11.15) дает

sin (11.16)

Воспользовавшись соотношениями (1.20) и (1.21а)

для равномерного распределения плотности тока, не-

сложно показать, что переменная составляющая скоро-

сти определяется соотношением

Таким образом, переменный ток пучка в любой точке

определяется через напряженность ВЧ поля и значения

в пространство взаимодействия:

{2) =

Щ { Е (х) "

М«-*>

dx +

* J vq

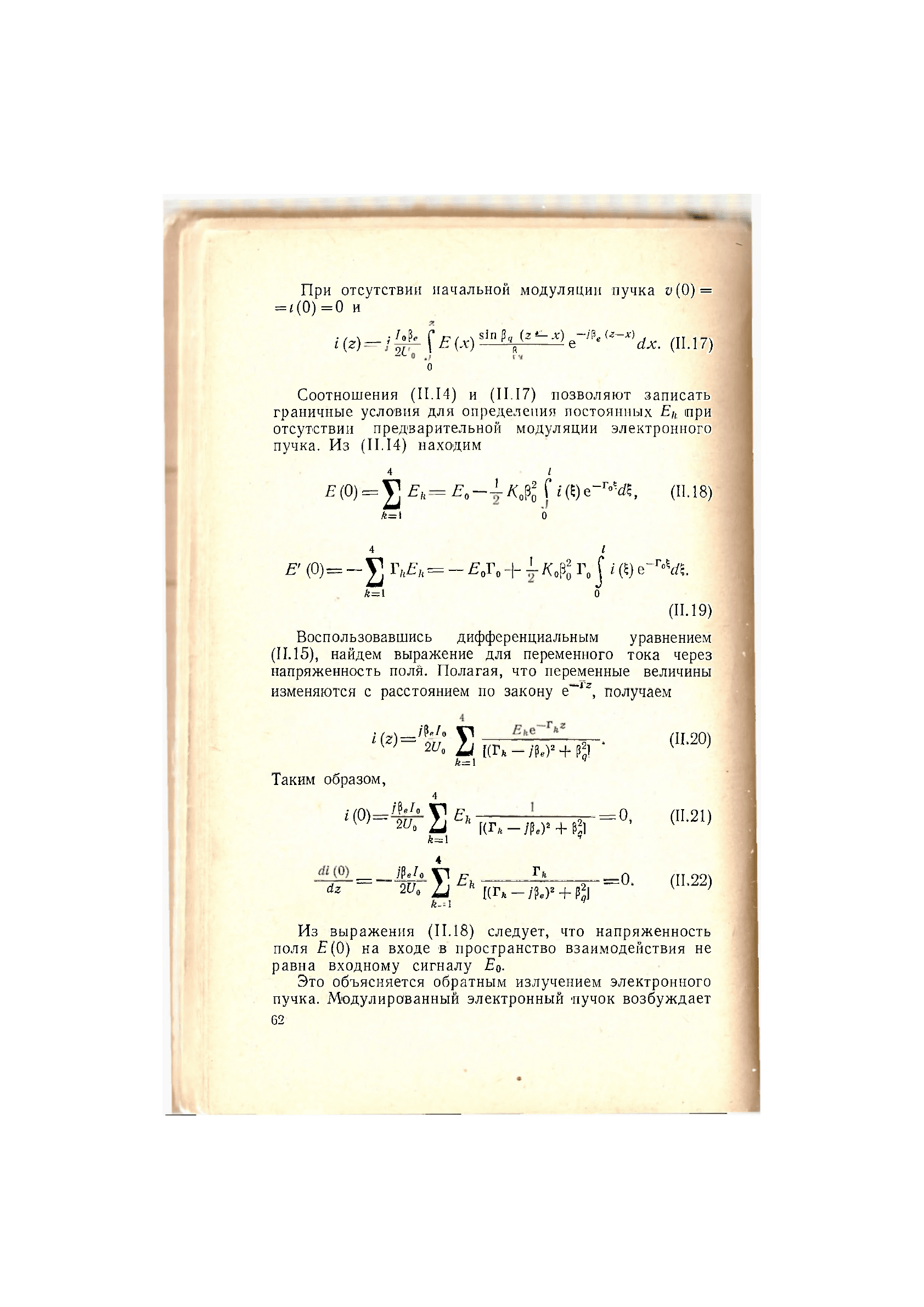
При отсутствии начальной модуляции пучка и(0) =

= г(0) =0 и

(2)

M|k (11.17)

Соотношения (II.14) и (11.17) позволяют записать

граничные условия для определения постоянных Ej

ори

отсутствии предварительной модуляции электронного

пучка. Из (11.14) находим

4 I

Е(0)Ще^Е

-± К

Г i (?) е-

<Я, (II. 18)

k=\ о

4 /

Е' (°)= ~ J]

= - Е

+1 Kofo

о j j

(?)

iffyfc

k=\ о

(11.19)

Воспользовавшись дифференциальным уравнением

(11.15), найдем выражение для переменного тока через

напряженность полй. Полагая, что переменные величины

изменяются с расстоянием по закону е"~

, получаем

i (z>='Ml у; —

. (ц.20)

и кг, - ,гу + Й

v }

k=\

Таким образом,

i(0)=!W±YE

— 5- = 0, (11.21)

2С/о и [(Г* - /р.)» + Й

k=\

f] Ш

=0. (11.22)

dz 2С/, Jj * [(Г, - /р

)

+ $

k —1

Из выражения (11.18) следует, что напряженность

поля -Б(О) на входе в пространство взаимодействия не

равна входному сигналу EQ.

Это объясняется обратным излучением электронного

пучка. Модулированный электронный -пучок возбуждает