Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

рпльно-проводящей цилиндрической поверхности при от-

сутствии пучка.

Дисперсионное уравнение для волн, распространяю-

щихся в спирально-проводящем цилиндре с пучком, по-

мещенном в волновод радиусом d\

впервые получено

Лошаковым [5]. В этом случае третья область вне спи-

рали ограничена: a<r< d\.

Дисперсионное уравнение имеет вид

/k Ctg ф\

и Ы) h Ы)

Кг

Ыг) — /

МО Кг Ы) ^

[ % J /,Ni)' ^ЫЖоЫ^-^ЫгЖоЫ)

Нг

Ы) + К

Ы) j;-

I = Н

' (1-67)

/о МО +

Ко

Ыг)

Нетрудно видеть, что'при d\ ->-оо уравнение (1.67)

переходит в (1.63). В (9] 'приведено дисперсионное урав-

нение для волн в спирально-проводящем цилиндре

с внутренним 'полым пучком. Оно имеет следующий вид:

[ТЬ

Кг

ш К

ш - xb

(ТЬ

) К

(т6

)]}

(та), (1.68)

где Ь

— соответственно внутренний и внешний ра-

диусы пучка;

(ТЬ,

%Ь)

— функция, которая получается из Н

пере-

становкой аргументов х и Г;

ЩЩ = ТЫ

(%Ь)

К, (ТЬ) + Mi (xb) Ко

(ТЬ).

(1.69)

При ii==0 уравнение (1.68) 'переходит в (1.63),

1.4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ

ДЛЯ ПОСТОЯННЫХ РАСПРОСТРАНЕНИЯ В СИСТЕМЕ

С ПУЧКОМ

Во втором параграфе было получено дисперсионное

уравнение для постоянных распространения в системе

с пучком методом самосогласованного поля [уравне-:

пие (1.32)]. Так как при выводе этого уравнения и дис-

персионного уравнения (1.63) сделаны одни и те же

• 31

где

1 х

— т

nb*-2It(Tb) ЩЩ

а M

— постоянная интегрирования.

Вне пучка составляющая E°

удовлетворяет уравне-

нию (1.76) без правой части. В этом случае выражение

для E°

может быть представлено в виде

Е°=М

(*Г) (Г>Ь)Г

где М

— вторая произвольная постоянная.

d Е

Используя непрерывность функций E

и на грани-

це пучка, при г =

находим значения постоянных

= — АН

, М

= АН

, (1.79)

где Н

и Н

определяются формулами (1.64).

Таким образом, поле E°

внутри пучка равно

E\^A[I

{Tr)-HJ^r)\. (1.80)

Для определения поля E'

можно воспользоваться

формулой (1.57), заменив Т на т. Опустив множитель

/(!)/—Г2

е , имеем

E'z = BJ

(хг) при r<a. (1.81)

Постоянную В\ можно выразить через М2, используя

гранитаые__условия на спирали (при г=а) для полного

поля Е=Е°+Е'. В результате несложных вычислений

получаем

R —

G\ta) '

где G(xa) определяется формулой (1.65).

Следовательно,

и г

- В!

Подставляя (1.82) и (1.80) в (1.75), находим выра-

жеиие для напряженности -поля внутри пучка

= A {/

Щ + [- Я, + /

(xr)}. (1.83)

Для вычисления коэффициента депрессии и сопротив-

ления связи найдем усредненное по сечению пучка зна-

чение напряженности поля

К (1.84)

Подставляя в (1.84) выражения для функций E

и гр

ИЗ (1.83) и (1.72), а также 'воспользовавшись известным

соотношением из теории беоселевых функций

х/

(ах) /

X [рх/„ (ах) I, (рх) - ах/, (осх) /

(рх)],

юсле несложных преобразований находим

Ш^ШШшШшш^

Ь I 2

Я,Я

н1

_7-2 а (ад) Р

—

)

(1.85)

где Л определяется соотношением (1.78).

Найдем теперь усредненное значение напряженности

поля по формуле (1.84), используя соотношения (1.18)

и (1.31):

КоГоР

•

КпГп

Р"

—Г^ Zj Т

—Щ /юе

фф

i(4i

где S

фф определяется соотношением (1.30).

Воспользовавшись определением коэффициента де-

прессии по формуле (1.36), запишем выражение для E

следующим образом:

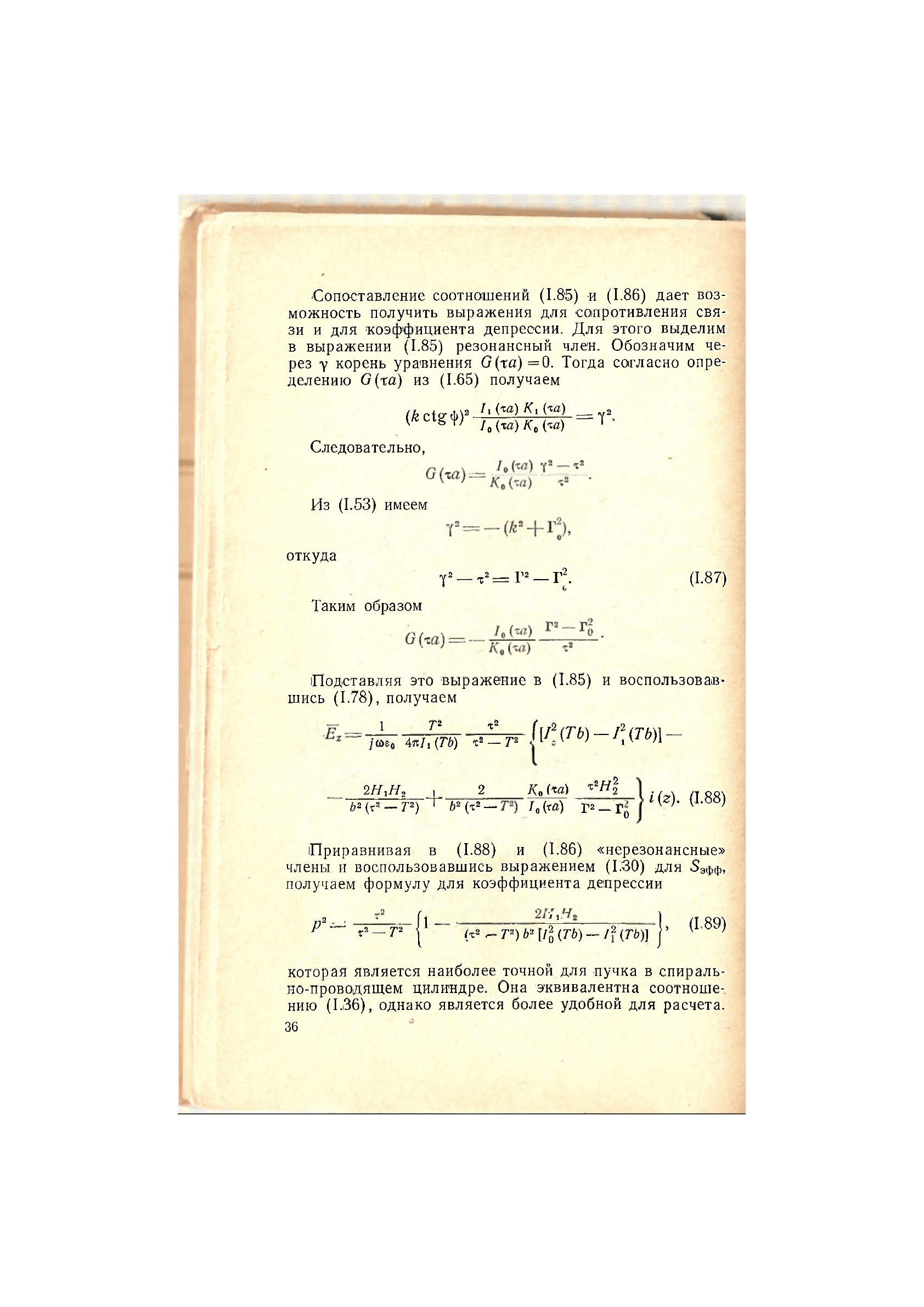
•Сопоставление соотношений (1.8'5) и (1.86) дает воз-

можность получить выражения для сопротивления свя-

зи и для коэффициента депрессии. Для этого выделим

в выражении (1.85) резонансный член. Обозначим че-

рез у корень уравнения G(xa) =0. Тогда согласно опре-

делению G(xa) из (1.65) получаем

(k ctff

Ф)

Jl Ы) КуЫ)

Ш Г

I* ctg щ 1

(ы)К

Ы) *

Следовательно,

Из (1.53) имеем

откуда

— х

=Г

— I* (1.87)

Таким образом

Подставляя это выражение в (1.85) и воспользовав-

шись (1.78), получаем

1 ш С

ЛТЬ)-1\{ТЬ)\

/соео AnIi(Tb) т

— Т

2Н

, 2 ЩШ

Ь2(

2) I fif

^? —/

И Г

/(г), (1.88)

Приравнивая в (1.88) и (1.86) «нерезонансные»

члены и воспользовавшись выражением (1.30) для 5

фф,

получаем формулу для коэффициента депрессии

—

2 __

2 jl — _

Т2) Ь2

у^щ _ j2

(Щ]

(189)

которая является наиболее точной для пучка в спираль-

но-проводящем цилиндре. Она эквивалентна соотноше-

нию (1.36), однако является более удобной для расчета.

Рассмотрим сначала случай малых токов. При этом

согласно (1.58) можно положить Т=т. Раскрывая не-

определенность, получаем выражение для р

/о

(rb)

- 1\

(гЬ)

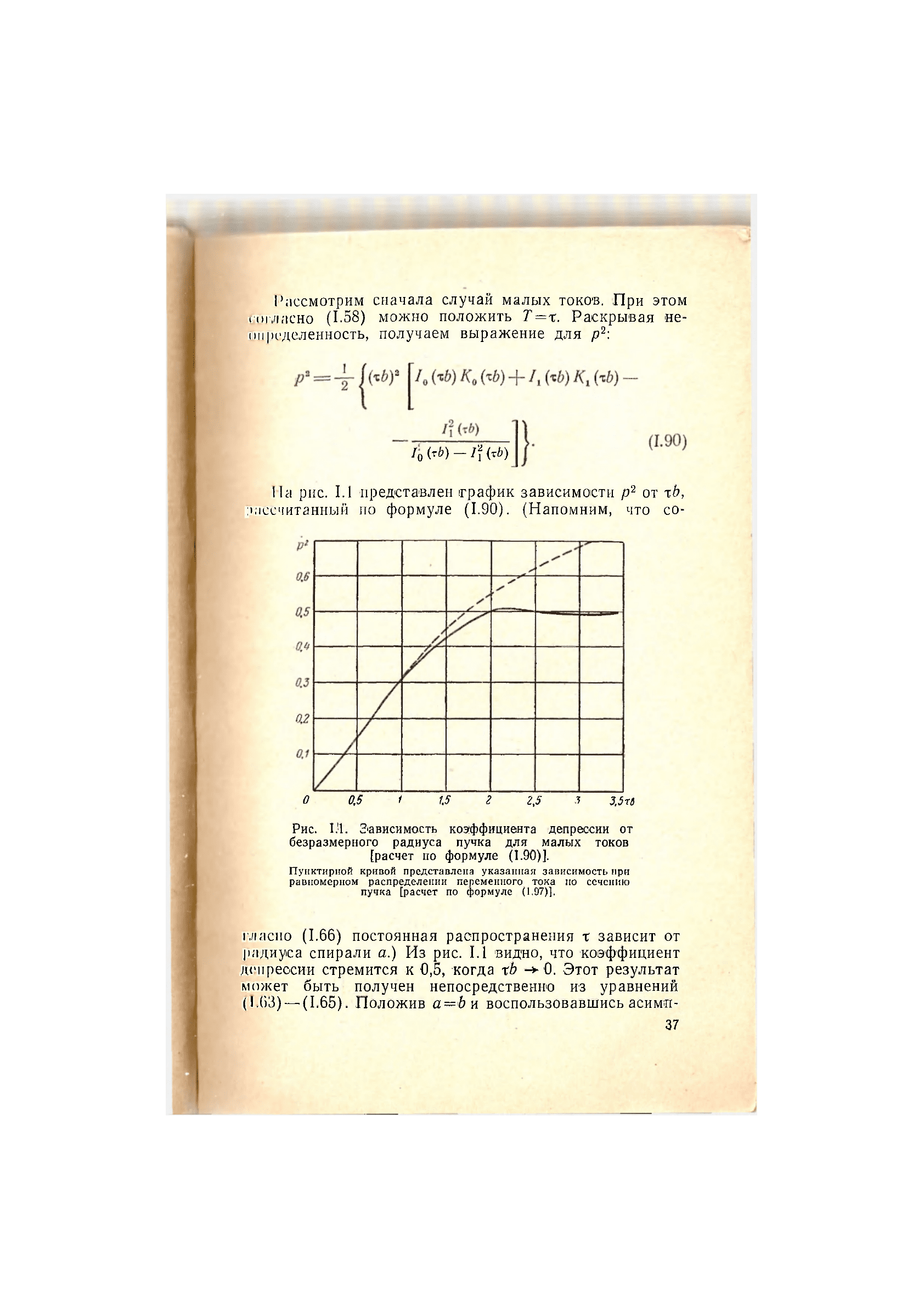
На рис. 1.1 представлен график зависимости р

от тЬ,

рассчитанный по формуле (1.90). (Напомним, что со-

0 0,5 1 1,5 2 2,5 3 3,5x5

Рис. 1Л« Зависимость коэффициента депрессии от

безразмерного радиуса пучка для малых токов

[расчет по формуле (1.90)].

Пунктирной кривой представлена указанная зависимость при

равномерном распределении переменного тока по сечению

пучка [расчет по формуле (1.97)].

гласно (1.66) постоянная распространения х зависит от

радиуса спирали а.) Из рис. 1.1 видно, что коэффициент

депрессии стремится к 0,5, когда xb 0. Этот результат

может быть получен непосредственно из уравнений

(1.63) — (1.65). Положив а=Ь и воспользовавшись асимп-

тотическими формулами для функций Бесселя при «боль-

ших значениях аргумента, из (1.63) — (1.65) 'получим

— у

Т +

(1.91)

где через у обозначен корень уравнения G(za) = 0, т. е.

в данном случае y = £-ctg<{>.

Решая уравнение (1.91) относительно —, находим

Воспользовавшись соотношением (1.58), после не-

сложных преобразований получим характеристическое

уравнение

(* - f)

1+^г

р:

Сопоставление этого уравнения с (1.32) в предположе-

нии —— 1 дает р

= 0,5.

Естественно, что для возможности определения по-

стоянных распространения из алгебраического уравне-

ния его коэффициенты должны зависеть только от «хо-

лодных» постоянных распространения и от параметров

пучка. Поэтому практический интерес представляют

приближенные соотношения для коэффициента депрес-

сии, выраженные через параметры холодной системы и

пучка. Сопоставление уравнений (1.32) и (1.63) дает воз-

можность получить достаточно точные дифференциаль-

ные соотношения для коэффициента депрессии и для

сопротивления связи. Эти соотношения получены в рабо-

тах [6, 9], и поэтому здесь мы их приводим без вывода:

Р'

j {m

[Л р к

до)+Ш щ к

/? Ж Y&

№) - Ш

Ko(Y^)

Iо (Y«)

F(fa)

2/? (Yb)

/о № - /? (y6)J I '

(1-Щ

D„K

o^c

fry ll

(V&)

—

№)

Ко

2 РЫп\ j

(уд)'

ГДС

—аГ* ^ (Y«)

A> =• /Г

5е

ш;

4 /.(г) /,(г) . Я, (г) /Ci (z)

г /

(г) 7, (г) Тд, (2) К

(г)

2 2 G' (г) '

(1.93)

(1.94)

(1.95)

(1.96)

и соответствующие производные вычисляются из (1.65)

с учетом (1.66). Из (1.63) и (1.66) следует, что для боль-

IX замедлений, когда -4- < 1,

= /Г

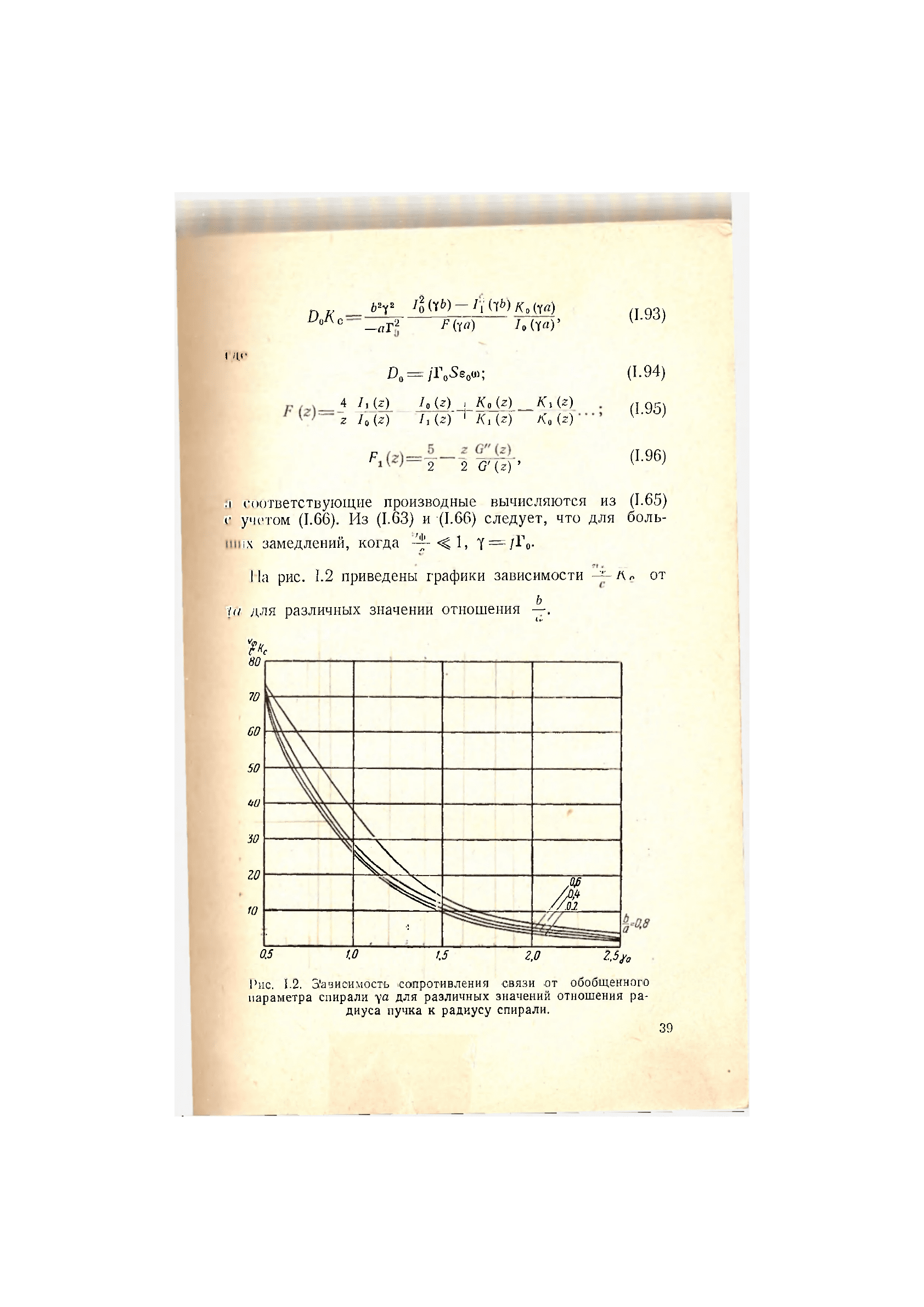
На рис. 1.2 приведены графики зависимости от

Yа для различных значении отношения —.

Ьс

во

го

ч\

№

/Л1

•

0.5

г,0

2,0

2,5*а

Рис. 1.2. Зависимость 'сопротивления связи от обобщенного

параметра спирали уа для различных значений отношения ра-

диуса пучка к радиусу спирали.

Сравнение формул (1.90) и (1.92) для коэффициента

депрессии [показывает, что они совпадают при малой

связи между пучком и системой. Заметим, что формулу

(1.92) можно получить также из (1.89), если воспользо-

ваться соотношением и перейти к пределу'

Однако раскрытие неопределенности при этом

приводит к очень громоздким вычислениям.

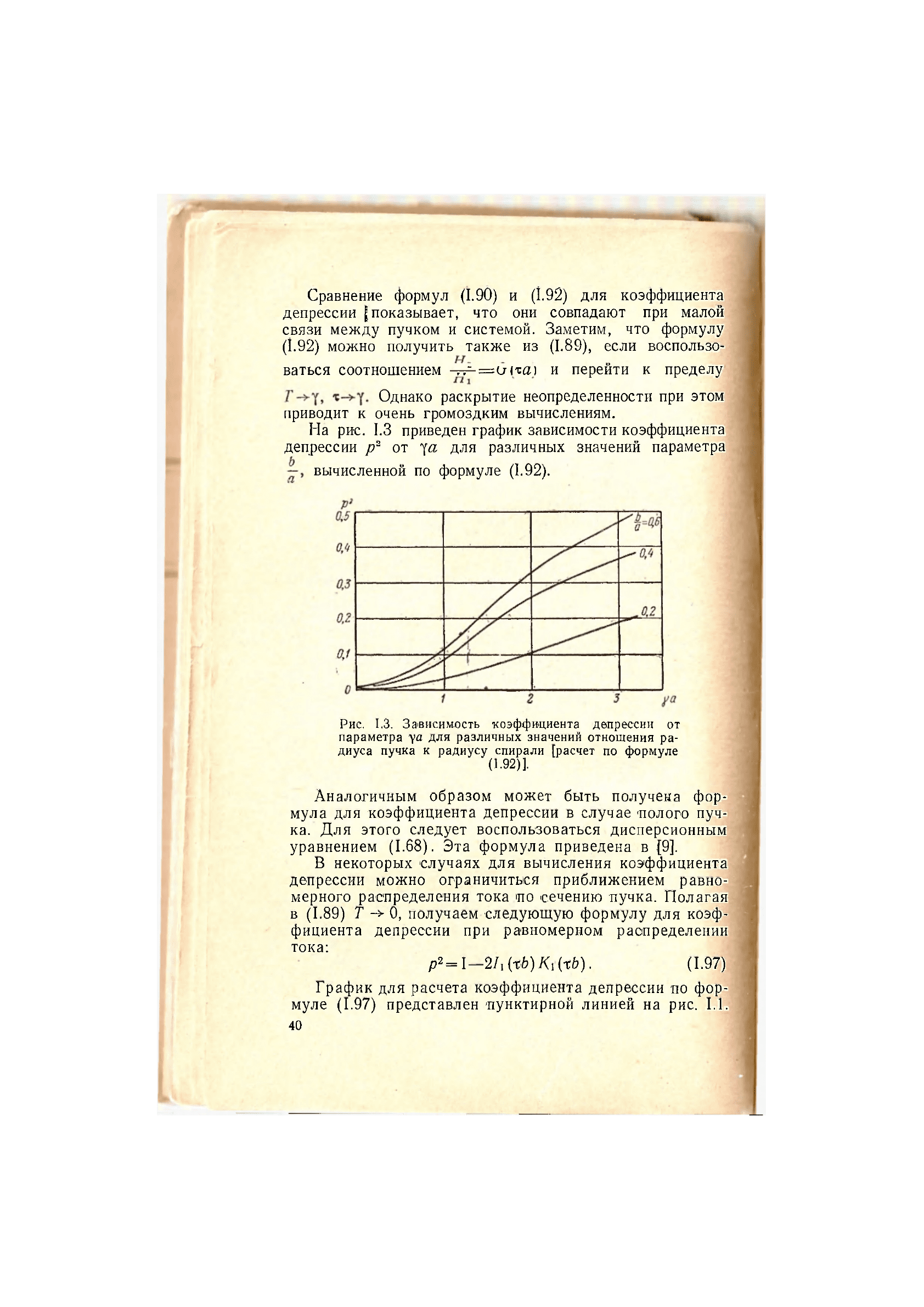
На рис. 1.3 приведен график зависимости коэффициента

депрессии р

от уа для различных значений параметра

вычисленной по формуле (1.92).

Рис. 1.3. Зависимость коэффициента депрессии от

параметра уа для различных значений отношения ра-

диуса пучка к радиусу спирали [расчет по формуле

(1.92)].

Аналогичным образом может быть получена фор-

мула для коэффициента депрессии в случае -полого пуч-

ка. Для этого следует воспользоваться дисперсионным

уравнением (1.68). Эта формула приведена в (9].

В некоторых -случаях для вычисления коэффициента

депрессии можно ограничиться приближением равно-

мерного распределения тока яго сечению пучка. Полагая

в (1.89) 7-^0, получаем следующую формулу для коэф-

фициента депрессии при равномерном распределении

тока:

=1—2/i (xb)Ki(xb). (1.97)

График для расчета коэффициента депрессии по фор-

муле (1.97) представлен 'пунктирной линией на рис. 1.1.

Обычно -в конкретных расчетах параметра простран-

ственного заряда вместо коэффициента депрессии вво-

дят коэффициент уменьшения плазменной частоты. Этот

коэффициент характеризует уменьшение плазменной ча-

стоты в электронном пучке, обусловленное конечными

поперечными размерами 'пучка и влиянием проводящих

стенок, окружающих лучок. Как известно, в бесконечно-

широком модулированном по скорости электронном по-

токе распространяются две волны 'пространственного за-

ряда, постоянные распространения которых определяют-

ся формулой

В пучке конечных поперечных размеров распростра-

ного заряда с постоянными распространения

где Rn — коэффициент уменьшения плазменной частоты.

Обычно ограничиваются рассмотрением первой пары

волн пространственного заряда. Для определения коэф-

фициента уменьшения плазменной частоты можно вос-

пользоваться формулами (1.53) и (1.58):

где Г — постоянная распространения волн простран-

ственного заряда;

Т — радиальная постоянная распространения в об-

ласти, занятой пучком.

В электронном пучке, движущемся с постоянной ско-

ростью, постоянная распространения — чисто мнимая

величина. Полагая Г=/|3, t=jT\ и предполагая, что

/г

/Р

< 1, имеем

Рпх

— —

= — (Г

+ &

) 1 +

(Г-/Ре)

Р о

^ •-• 02

Р 1

(Р —

Ре)

откуда

V1 +

т\\р

Расчет показывает, что при обычных условиях

т. е. Поэтому в первом приближении

Ре

можно записать

где

/?=

=• (1.98)

V\ +T\if

Для определения коэффициента уменьшения плаз-

менной частоты необходимо определить радиальную по-

стоянную распространения -в пучке. Зта задача для

Рис. 1.4. Зависимость квадрата .коэффициента

уменьшения плазменной частоты от параметра

рей для различных отношений радиуса пучка

к радиусу цилиндра.

сплошного пучка радиусом Ь

помещенного в трубу ра-

диусом а, впервые решена Ханом и Рамо [17, 18]. При

этом получено следующее трансцендентное уравнение

для постоянной распространения;