Цейтлин М.Б., Кац А.М. Лампа с бегущей волной

Подождите немного. Документ загружается.

• и

чем*

ки не зависит от параметра усиления. Это обуслов-

лено тем, что на начальном участке взаимодействие сла-

бое, так как ток сгруппированного пучка мал.

Рассмотрим решение задачи о взаимодействии элек-

ройного потока с 'бегущей волной в пренебрежении

оОрлтиым излучением. В этом случае уравнение возбуж-

д#ПИЯ длинной линии запишется следующим образом:

(г) = Е^-Щ-,

(6) е

® Л. (11.44)

Дифференцируя по 2, получаем

dE кй

• "j±

= *±Цг)..

(11.45)

Дифференциальное уравнение для сгруппированного

Потока остается без изменения;

г £+'=/Ik<

11Л5

Решая эту систему, приходим к следующему харак-

теристическому уравнению для постоянных распростра-

нения Г в системе с пучком:

Г (Г - Г

)[(Г-iU + % ] - /Мо С

— 0. (11.46)

Таким образом, при пренебрежении обратным излу-

чением поле в системе с пучком может быть представ-

лено суперпозицией трех волн. Отсюда следует, что про-

исхождение четвертой волны (фазовая скорость кото-

рой противоположна скорости электронного пучка) не-

посредственно связано с обратным излучением электрон-

ного потока.

Воспользовавшись (II.2) и (II.3), находим

Ь' • 8

+ /г8

+ <78 Щ /

[(1

+ ьсу + rq] =»

(11.47)

Сопоставление этого уравнения с уравнением (11.12)

показывает, что они не совпадают. Это означает, что

обратной излучение электронного потока проявляется не

только в изменении граничных условий, но и в измене-

нии постоянных распространения волн в системе I пуч-

ком. Однако решение уравнения (11.47) показывает, что

корни этого уравнения практически не отличаются от

корней уравнения (11.12). (Различием значениях корней

не превышает 2%.)

Таким образом, для расчета коэффициента усиления

при больших значениях параметра С (при отсутствии

затухания) можно пользоваться формулами (11.29) —

(11.31) и графиками, изображенными на рис. 11.14—

11.16 и 11.20.

II.4. ВЛИЯНИЕ РАСПРЕДЕЛЕННОГО ЗАТУХАНИЯ

НА КОЭФФИЦИЕНТ УСИЛЕНИЯ

В предыдущих параграфах рассматривалось усиле-

ние при отсутствии затухания в замедляющей системе

(d=О). В этом случае, как было показано, коэффициен-

ты характеристического уравнения вещественны и реше-

ние его не представляет больших затруднений. При на-

личии распределенного затухания характеристическое

уравнение содержит комплексные коэффициенты и реше-

ние его весьма затруднительно. Поэтому желательно

иметь метод, позволяющий определить коэффициент

усиления, не решая характеристического уравнения,

а используя граничные условия и связь между коэффи-

циентами и корнями характеристического уравнения.

Одним из таких методов является метод рядов [5, 6].

В дальнейшем нам понадобятся выражения для на-

пряженности поля, переменных составляющих тока и

скорости при наличии предварительной модуляции пуч-

ка. Для определения амплитуд парциальных волн запи-

шем граничные условия при наличии предварительной

модуляции. Эти граничные условия могут быть записаны

на основании соотношений (11.14) и (11.16). Для упро-

щения будем пренебрегать обратным излучением. (При

наличии затухания -в системе пренебрежение обратным

излучением вполне обосновано.) В этом случае поле

представляет собой суперпозицию трех парциальных

волн:

^Шр (11*48)

k=\

.74

ШЙШт Щ

k=\ *

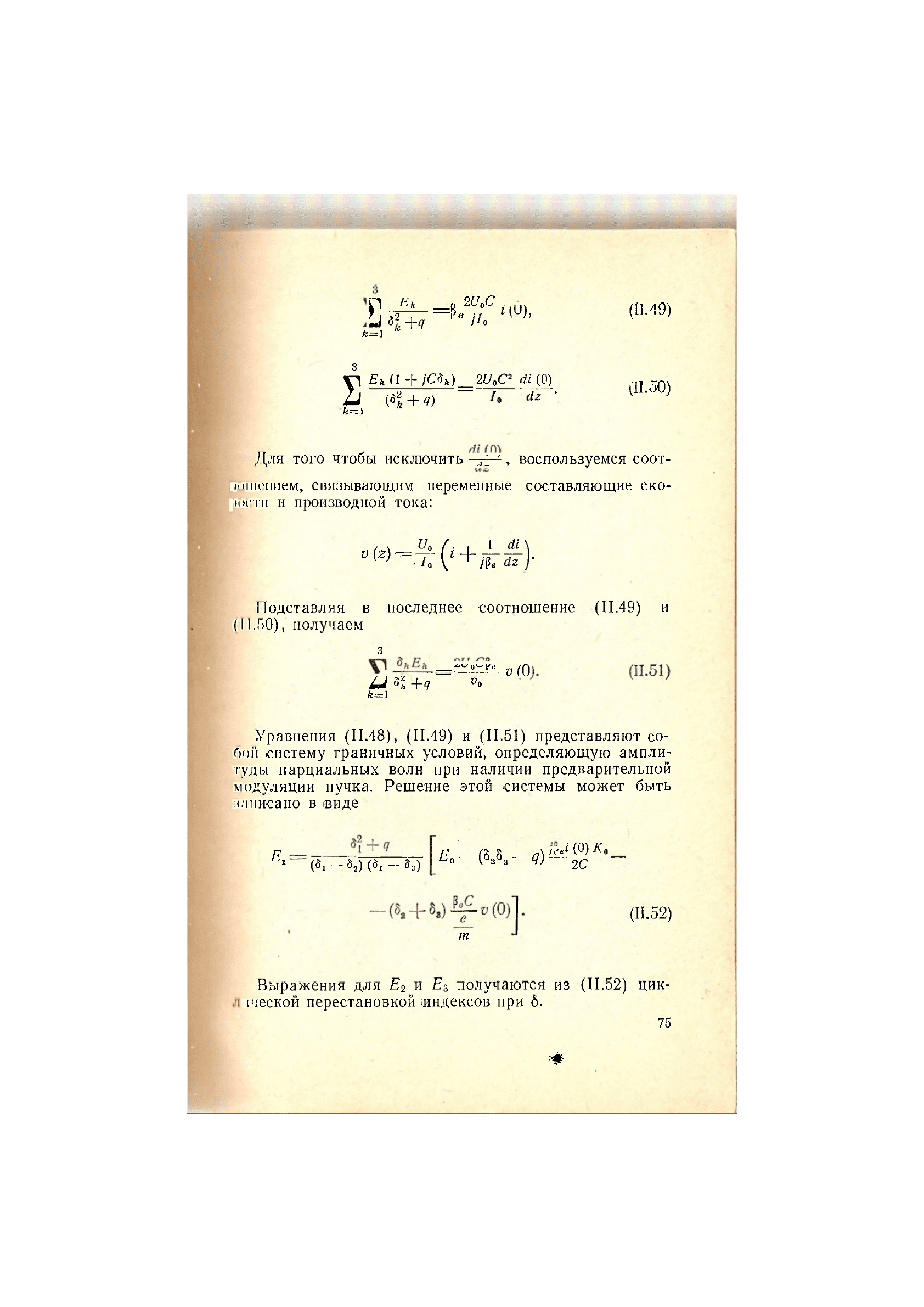
(\+jC3

)

(0)

50)

(

j2 ,

}

/, dz •. mm

, (»*+?>

k=.\

Для того чтобы исключить • воспользуемся соот-

юшением, связывающим переменные составляющие ско-

рости и производной тока:

тшш

Подставляя в последнее соотношение (11.49) и

(11.50), получаем

= 0

LA К +q

k=l

Уравнения (11.48), (11.49) и (11.51) представляют со-

бой систему граничных условий, определяющую ампли-

туды .парциальных волн при наличии .предварительной

модуляции пучка. Решение этой системы может быть

записано в виде

(»!

—

».) (S. -Зз)

ШШШтШШ.

(11.52)

Выражения для Е

и Е

получаются из (11.52) цик-

дческой перестановкой индексов при б.

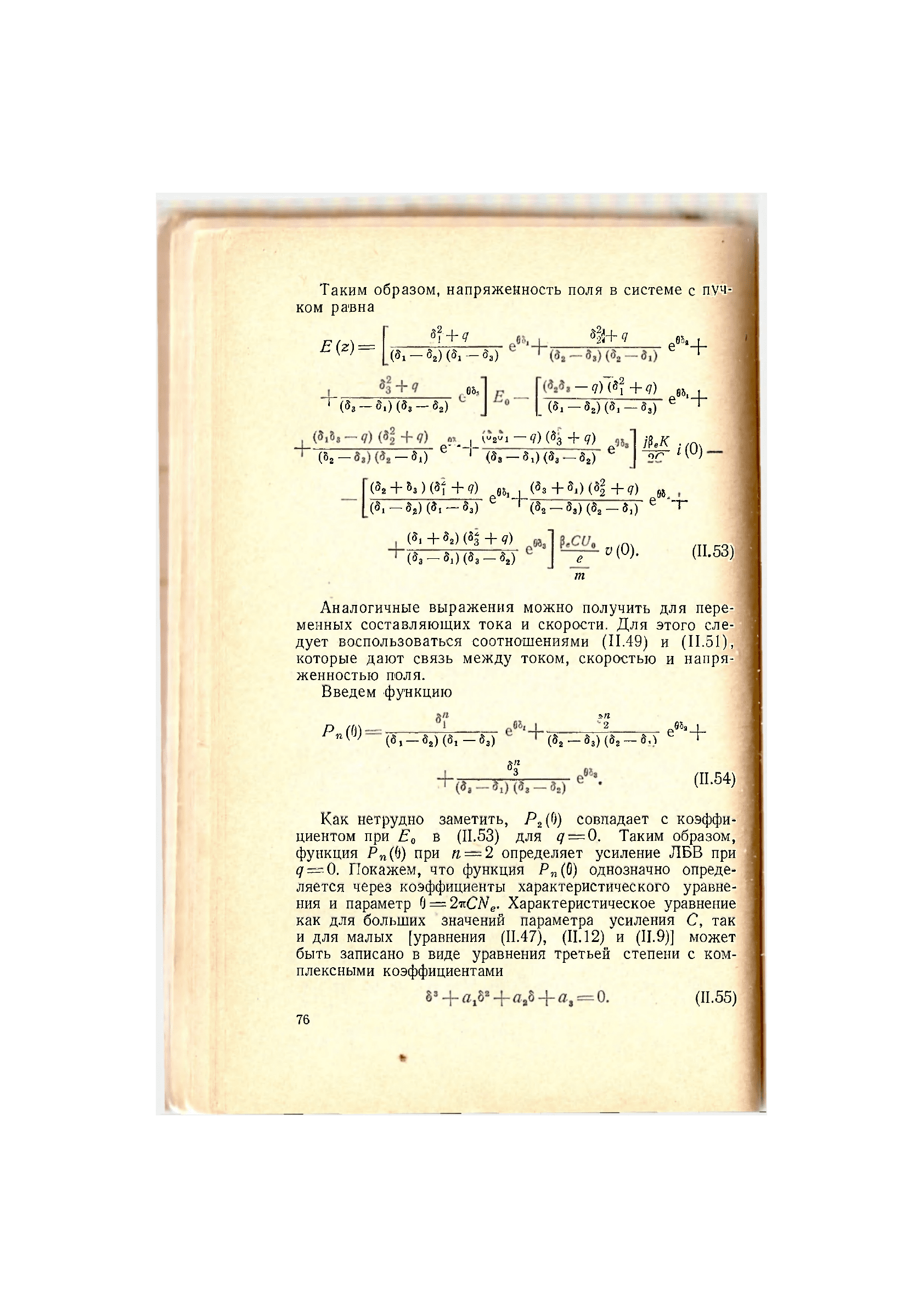
Таким образом, напряженность поля в системе с гш|

ком равна

Е{г) =

Sf+<7

Ш'д

(«1—а,) («1-е.)

65,

I (S

—в,) (5

—9

)

- д)1*\ + я)

(»,-«,)(в,-в,)

в5

вг

(». ——«О

I - 9)

(

+ <?)

6 "[""Ti

/» вт- в

(«I —»i) («.

—

а.)

в!

Ч-

ША

(*»

+ »«) (8f +

и,. (».+*.) (tf +9) „,

(а,-а,)(в,-а,)

""I" («,-«,) (а,-в,)

"г

(». + а,) (Д| +

<?)

—а,)(а

—а

)

*<0).

(11.53)

Аналогичные выражения можно получить для пере-:

менных составляющих тока и скорости. Для этого еле-:

дует воспользоваться соотношениями (11.49) и (11.51),

которые дают связь между током, скоростью и напря-

женностью поля.

Введем функцию

Рп{ 6)

«ДО») (*i-*i)

&п

(д

— д

)

(д

~дл

е5

°3

(11.54)

Как нетрудно заметить, Р

{6) совпадает с коэффи-

циентом при £*

в (11.53) для q =0. Таким образом,

функция Р

(6) при п = 2 определяет усиление ЛБВ при

q = 0. Покажем, что функция Р

(8) однозначно опреде-

ляется через коэффициенты характеристического уравне-

ния и параметр

2nCN

Характеристическое уравнение

как для больших 'значений параметра усиления С, так

и для малых [уравнения (11.47), (11.12) и (II.9)] может

быть записано в виде уравнения третьей степени с ком-

плексными коэффициентами

(11.55)

.76

Представим экспоненциальные мйожители е

в виде

гепеннрго ряда

6 ъ„

«I

т=0

Тогда функция Р„(9) запишется следующим образом:

r (de

ЩЦ

п+т

(5g

_ g|

п+т

оо

п(6)

т!

S-Ж-Ш ттшттт

т=О

Введем

ЩЬ» (8, - 8

) (8

- 8J р| 1

Легко показать, что D

= D

— 0, а

= — — S

) (8

— 8

) (S

— SJ.

Тогда

р ЩЩ^Й °п+ш

•

ш=О

(11.56)

(Н.57)

(11.58)

Покажем, что коэффициенты можно выразить че-

рез коэффициенты характеристического уравнения

(11.55). Для этого, подставив в (11.55) значения корней,

получим три тождества:

i + -f «2

1 + «з =

(11.59)

Умножим первое тождество на 8" (3

—г|§

), второе—на

i"(8

—SJ, третье —- на 8"

(Ь

— 8

) и сложим результаты:

(

з -

з) +

(К -

х) +

(

, - У +

[

•(«,

з) +

МП + Г

Щ -

з)1

Е 1

Г' (

2 -

з) +

(

> -

i) +

(

! I

*)]+

+ «з (К (К -

з) +1(

з - 8.) +

ИЙЙЙ

.77

Воспользовавшись определением коэффициентов

получаем соотношение

+8+a

n+l

+ a

=О, (II .60)

которое является реккурентной формулой для D

. Так

как £)i=Do=0, то это соотношение позволяет выразить

коэффициент D

с любым значением индекса п (как по-

ложительным, так и отрицательным) через коэффициент

И коэффициенты характеристического уравнения. Из

(11.58) следует, что функция Р

(6) определяется отно-

шением коэффициентов и D

. Таким образом, функ-

ция Р

(0) однозначно определяется через 'коэффициен-

ты характеристического уравнения (11.55) и параметр б.

Для того чтобы записать выражение для напряжен-

ности поля через функцию Р

(б) и коэффициенты ха-

рактеристического уравнения, воспользуемся соотноше-

ниями между корнями и коэффициентами уравнения

третьей степени. Эти соотношения напишем следующим

образом:

2 +

= —

— Ц

Подставляя эти соотношения и (II.54) в (11.53), пос-

ле несложных преобразований получаем выражение для

напряженности ВЧ поля E(z):

Е (Z) = (Л + qPo) Ео + [а,р + Р

-f

Щщ + Р

] X

X ^ fо + [йзЛ + qP

Щ(а

Р_(+qP

)} jjfl(0). (II.61)

Для переменных составляющих тока и скорости мо-

гут быть записаны аналогичные выражения. Для этого

следует воспользоваться формулами (11.49) и (11.51) и

проделать аналогичные преобразования. В результате

получим

f,u,c

v (Z)

л + («Л + Л)Щж

(0) +

+ (^0 + ^)^-/(0), (11.62)

.78

Ma i

(z) =

+ (

fll

+ Щ v (0) +

[ (П.63)

Так как функция P

(Q) выражается при помощи

ряда (11.58), то напряженность поля и переменные состав-

ляющий тока и скорости можно представить в виде сте-

ионного ряда по 9. Как известно, ряд V-^- сходится до-

т=О

польно быстро при 9<1. Обычно длина участка взаимо-

действия соответствует значениям 1). Кроме

того, сходимость ряда (11.58) ухудшается наличием ко-

эффициентов

, которые возрастают с ростом т. По-

JJ 2

Этому для вычисления напряженности поля следует брать

и разложении достаточно много членов ряда, что не-

удобно. В связи с этим приходится разбивать участок

взаимодействия на несколько частей и вести расчет для

каждой части. Если длина участка соответствует значе-

нию

= 0,628(СЛ/

= 0,1), то для расчета достаточно

брать 2—5 членов ряда, в зависимости от значений па-

раметров q, by d и С.

При этом значения напряженности ВЧ поля и пере-

менных «составляющих тока и скорости на конце уча-

стка являются начальными для следующего участка.

Поэтому -необходимо иметь выражения для величин

E(z)

i(z) и v (z) при наличии предварительной модуля-

ции электронного пучка.

Таким образом, метод рядов позволяет рассчитать

зависимость переменных составляющих напряженности

поля, тока и скорости при заданном распределении пара-

метров прибора вдоль участка взаимодействия. Этот ме-

тод можно применить также для расчета коэффициента

усиления ЛБВ с локальным затуханием. Этот вопрос

будет рассмотрен в следующем параграфе.

Рассмотрим влияние затухания на усиление при ма-

лых значениях параметра усиления. Из характеристиче-

ского уравнения (II.9) -следует

=jr=jb+d, a

=q, a

=j{l+qr). (11.64)

.79

Задаваясь конкретными значениями параметров Ь

q и d, вычисляем по формулам (11.61) — (11.63) значе-

ния переменных составляющих напряженности поля,

тока и скорости. Длина каждого участка соответствует

значению CN=0,1. Для расчета-начального участка при-

ЩШ

-2

а* 0J

щи

/ /

/ 1

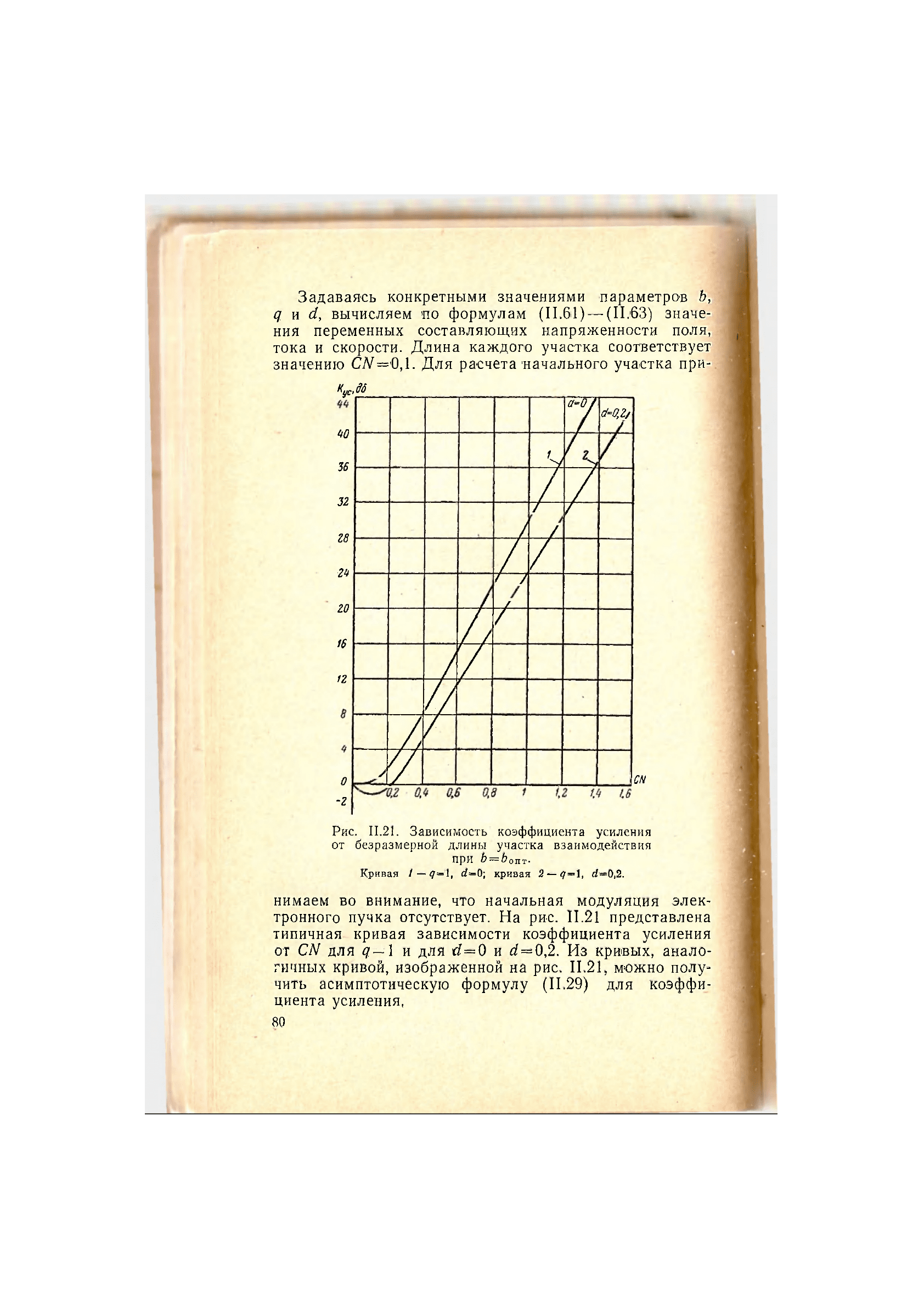
Рис, 11.21. Зависимость Коэффициента усиления

от безразмерной длины участка взаимодействия

При Ь = Ьопт.

Кривая / — <7='l, с£=0; кривая

2—•

<7=1, d=0,2.

нимаем во внимание, что начальная модуляция элек-

тронного пучка отсутствует. На рис. 11.21 представлена

типичная- кривая зависимости коэффициента усиления

от CN для q

— 1

и для d=0 и d=0,2. Из кривых, анало-

гичных кривой, изображенной на рис. 11.21, можно полу-

чить асимптотическую формулу (11.29) для коэффи-

циента усиления,

.80

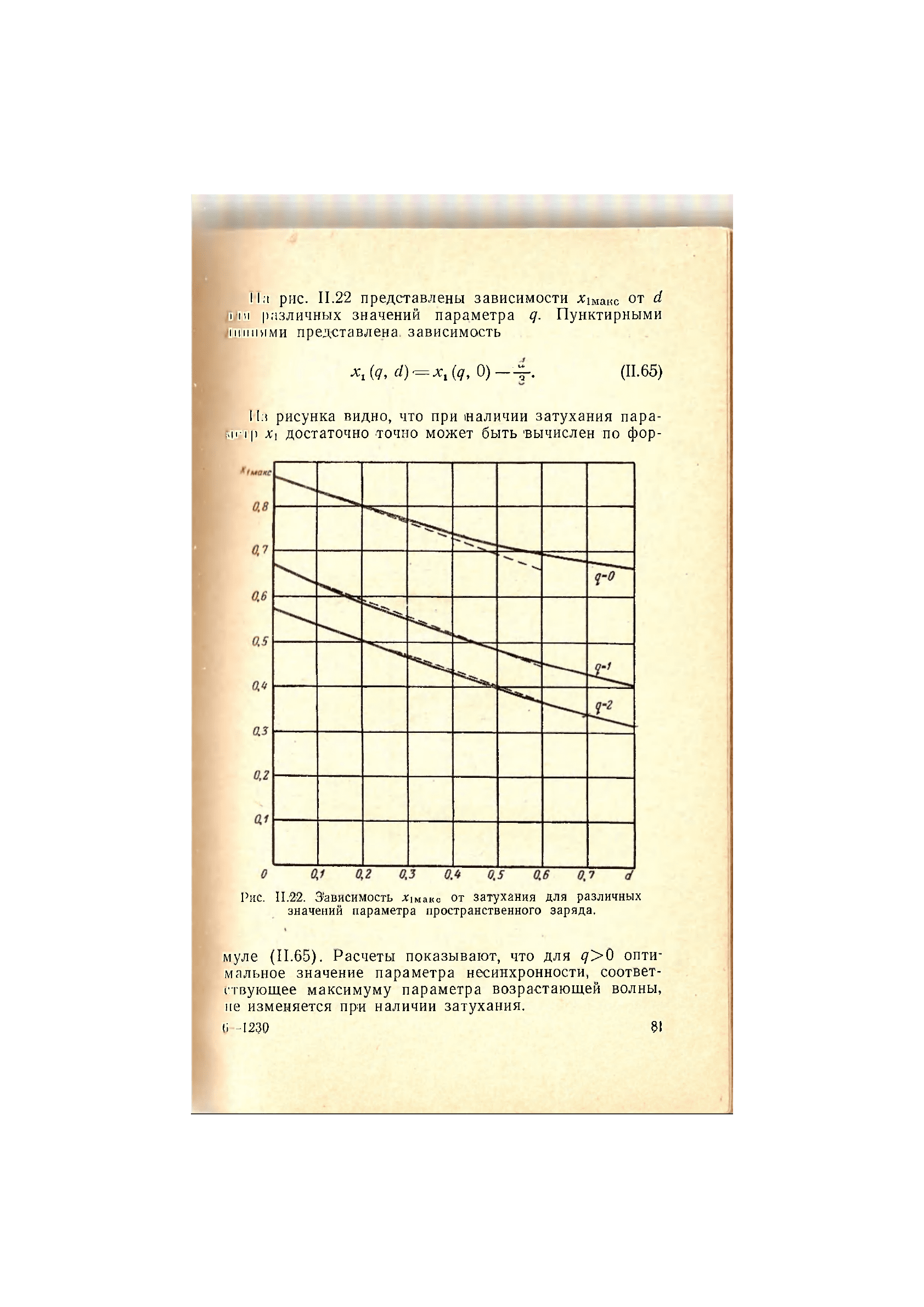
На рис. 11.22 представлены зависимости ЩЩщ от d

дли различных значений параметра q. Пунктирными

Линиями представлена, зависимость

V Щ

(<7,

d) Щх

0) (11.65)

Из рисунка видно, что при наличии затухания пара-

метр Х\ достаточно точно может быть 'вычислен по фор-

Рис. 11.02. Зависимость ломаке от затухания для различных

значений параметра пространственного заряда.

муле (11.65). Расчеты показывают, что для <7>0 опти-

мальное значение параметра несинхронности, соответ-

ствующее максимуму параметра возрастающей волны,

не изменяется при наличии затухания.

6—1230 81

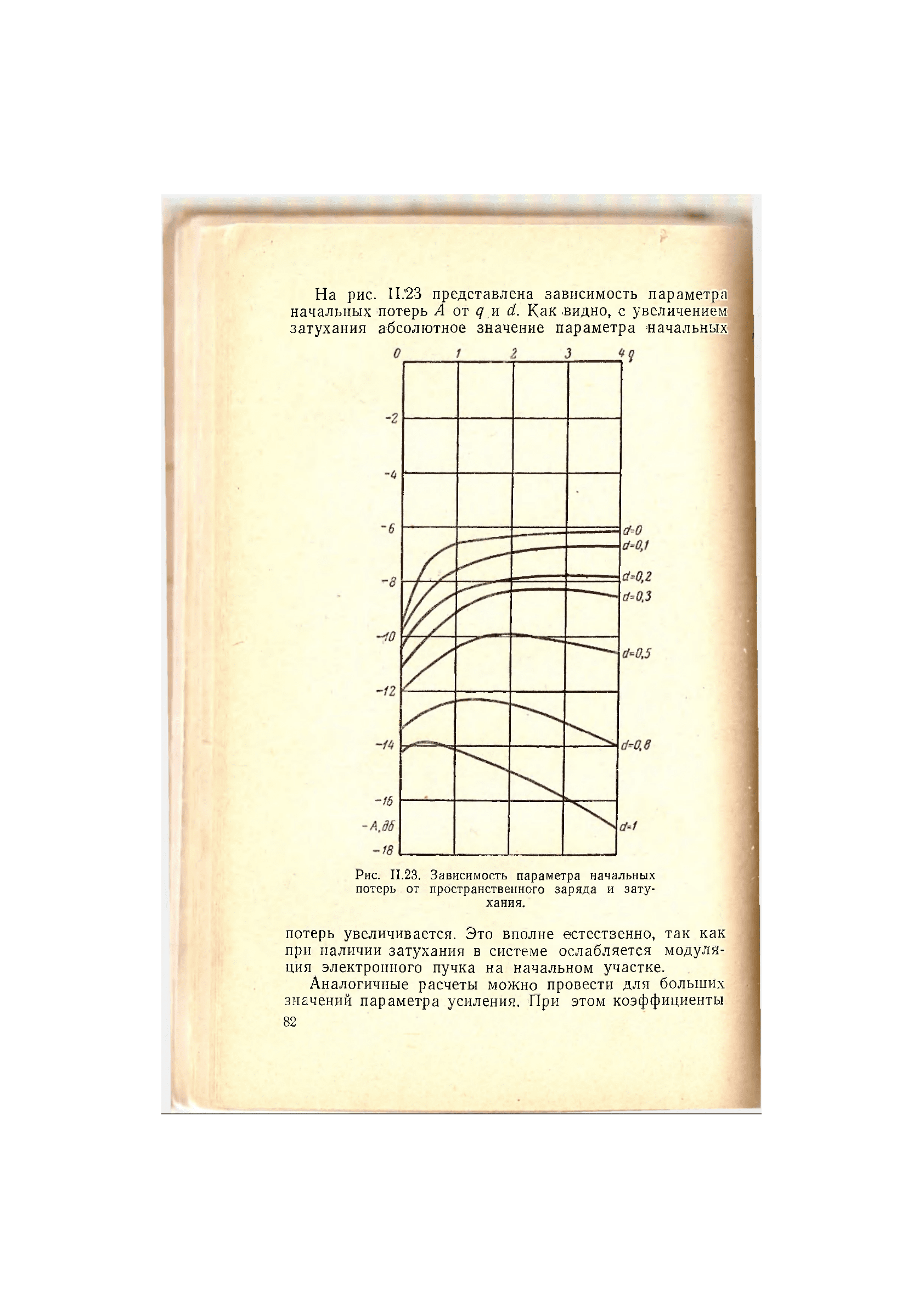
На рис. II23 представлена зависимость параметра

начальных потерь А от q и d. Как .видно, с увеличением

затухания абсолютное значение параметра -начальных

Рис. 11.23. Зависимость параметра начальных

потерь . от пространственного заряда и зату-

хания.

потерь увеличивается. Это вполне естественно, так как

при наличии затухания в системе ослабляется модуля-

ция электронного пучка на начальном участке.

Аналогичные расчеты можно провести для больших

значений параметра усиления. При этом коэффициенты

.82