Castilho Leda R., Moraes Angela Maria (Ed.) Animal Cell Technology: From Biopharmaceuticals to Gene Therapy

Подождите немного. Документ загружается.

ent cell lines and experimental conditions (operation mode, media formu-

lation, initial conditions, etc.) may inﬂuence the ﬁtting of parameters and,

consequently, different parameter values are expected for the same phe-

nomena. Table 8.2 presents parameter values ﬁtted for models of Table 8.1

from speciﬁc experimental conditions. These are indicative of the range of

values they can assume for animal cell systems. However, some of these

values may be considered inappropriate. This is the case of the value ﬁtted

for 

X,max

in Equation 40 – 0.125 h

–1

– surely a value not representative

for an animal cell system.

Kinetic formulations for animal cell death

Necrosis and apoptosis, the two mechanisms of cell death, are discussed

extensively in Chapter 7, and are considered in more detail in this section.

Cell death is particularly important for animal cell systems, considering

their intrinsic fragility in the imposed culture conditions, mainly as a result

of hydrodynamics shear stress and media composition. This scenario is

very different from that of microbial systems, for which it is rare to ﬁnd

formulas representing death processes. When establishing culture condi-

tions for animal cells, there is always much concern in minimizing injury

to cells, to insure high viabilities for long periods. Nevertheless, modiﬁca-

tions in the environment, mainly in media composition, occur during the

culture that normally lead to loss of viability. That explains why many

Table 8.2 Fitted parameters for models in Table 8.1

Eq. 

X,max

–1

)

GLC

(mM)

GLN

(mM)

i,LAC

(mM)

i,NH3

(mM)

Other parameters

(37) 0.036 – 0.06 – – –

(38) 0.045 1 0.30 – – –

(39) 0.033 0.278 – 13.9 – –

(40) 0.125 – 0.8 8.0 1.05 –

(41) 0.063 0.15 0.5 140 20 –

(42) – – 0.0309 – –



X,min

¼ 0.013 h

–1

;

GLC

Limiar

¼ 0.0303 mM

(43) 0.056 0.06 ––––

(44) 0.055 – 0.15 – –

Serum

)

¼26.5;

¼0.21;

i,NH

¼ 26 mM

(45) – – – – –

¼ 0.043 h

–1

;

¼ 0.07 g/L

(46) – – – – –

¼ 0.0029 h

–1

;

¼ 0.0195 h

–1

;

(47) 0.045 to 0.072 0 to 0.0094 0 to 0.040 – – 0.0043< Æ

< 0.0092

(L/10

cel.h)

202 Animal Cell Technology

models incorporate the inﬂuence of substrates and products in their equa-

tions to simulate death kinetics (Table 8.3).

Similar to what has been shown in Table 8.1 for speciﬁc growth rate,

many mathematical expressions listed in Table 8.3 employ Monod-type

structures for limiting phenomena, and Aiba and Shoda-type structures

for inhibitory behavior. Limiting components for cell death are lactate and

ammonia, that is, the presence of these byproducts increases the speciﬁc

cell death rate. On the other hand, substrates, such as glucose and

glutamine, inhibit cell death (Equations 48 to 52).

Similar to what was shown for growth, some models establish a linear

relationship between the speciﬁc death rate (k

) and an autoinhibitory

product synthesis (Lee et al., 1995). This autoinhibitory product is

represented by the expression X

=D, where X

is a viable cells concentra-

tion, measured in terms of cell number per volume, and D is the speciﬁc

feed rate that plays the part of substrate supply to the culture. By setting

=

as a function of X

=D (where X

is a total cell concentration) it is

possible to build up a more robust model that can ﬁt a larger amount of

experimental data (Equation 56) (Zeng et al., 1998).

Table 8.3 Kinetic expressions for speciﬁc cell death rate in animal cell systems

Formulations References Eq.

¼ k

d,max



þ NH



LAC

þ LAC

Batt and Kompala, 1989 (48)

¼ k

d,max



þ NH



LAC

þ LAC



i,GLN

þ GLN

Bree et al., 1988 (49)

d,max

(

X,max

 k

d

LAC

 LAC)  (

X,max

 k

d

 NH

)



i,GLN

þ GLN

de Tremblay et al., 1992 (50)

¼ k

d,min

þ (k

d,max

 k

d,min

) 

i,GLN

þ GLN

Dalili et al., 1990 (51)

¼ (

X,min

 D

min

)  k

d,max



(GLC  GLC

thres

)

GLC

þ (GLC  GLC

thres

)

Frame and Hu, 1991a. (52)

¼ b

GLN þ b

Po¨rtner et al., 1996 (53)

¼ c

 e



Glacken et al., 1989 (54)

¼ d

 e

=

)

Linardos et al., 1991 (55)

¼ (

þ 

 

) 

Zeng et al., 1998 (56)

Adapted from Po¨rtner and Scha¨fer, 1996). X t, total cell concentration measured as total cell number per volume

(10

cell/ml).

Mathematical models for growth and product synthesis in animal cell culture 203

Table 8.4 lists parameter values ﬁtted to models presented in Table 8.3.

Formulations for substrate uptake

Generally, the expressions proposed for the kinetics of glucose or gluta-

mine uptake do not differ signiﬁcantly from each other. Table 8.5 (for

formulations) and Table 8.6 (parameters) sum up the kinetic models for

the description of substrate uptake rates.

Pirt’s formulations, or variations of them (see Equation 26), were

employed in many models shown in Table 8.5. In one of them (Equation

59) the term e

is added to better ﬁt data obtained at low speciﬁc

growth rate (Linardos et al., 1991). Other propositions introduced a

minimum speciﬁc growth rate (

X,min

) to ﬁt the non-linearity observed at

the same low speciﬁc growth rate (Frame and Hu, 1991a, 1991b).

For Equations 62 and 63, the maintenance coefﬁcient appears limited by

substrate through a Monod-type formulation.

Finally, in Equation 64, Zeng (1996a) modiﬁed his own original model

(presented in Equations 28 to 30), by eliminating parameter S* that

assumes low values for hybridomas culture. The inﬂuence of nutrients is

dependent, not on nutrient concentration, but on available mass of

nutrient per cell unit S=X

Formulations for product synthesis

Table 8.7 (mathematical expressions) and Table 8.8 (parameters) review

the main models found in the literature for the representation of product

Table 8.4 Fitted parameters for models of Table 8.3

Eq. k

d,max

–

(mM)

LAC

(mM)

i,GLN

(mM)

Other parameters

(48) 0.08 1.44 311 –

(49) 0.0833 1.44 15 5.10

–4

–

(50) 0.0288 – – 0.02

d

¼ 0.0025 (1/mM.h);

d

LAC

0.00042 (1/mM.h)

(51) 0.08 – – 5.10

–6

d,min

¼ 0.05 h

–1

(52) 0.00628 – – –

min

¼ 0.00636 h

–1

;



min

¼ 0.013 h

–1

;

GLC

¼ 0.240 mM

(53) ––––

¼ 0.002 h

–1

¼ 6.10

g/L.h;

¼ 0.0025 g/L

(54) 0.051 – – – c

¼ 0.051 h

–1

¼ –101.2 h

(55) – – – d

¼ 0.0029 h

–1

¼ 0.0195 h

–1

(56) ––––

0.0< 

< 4.6.10

–5

–1

0.0< 

< 0.0038 L/10

.cel.h

204 Animal Cell Technology

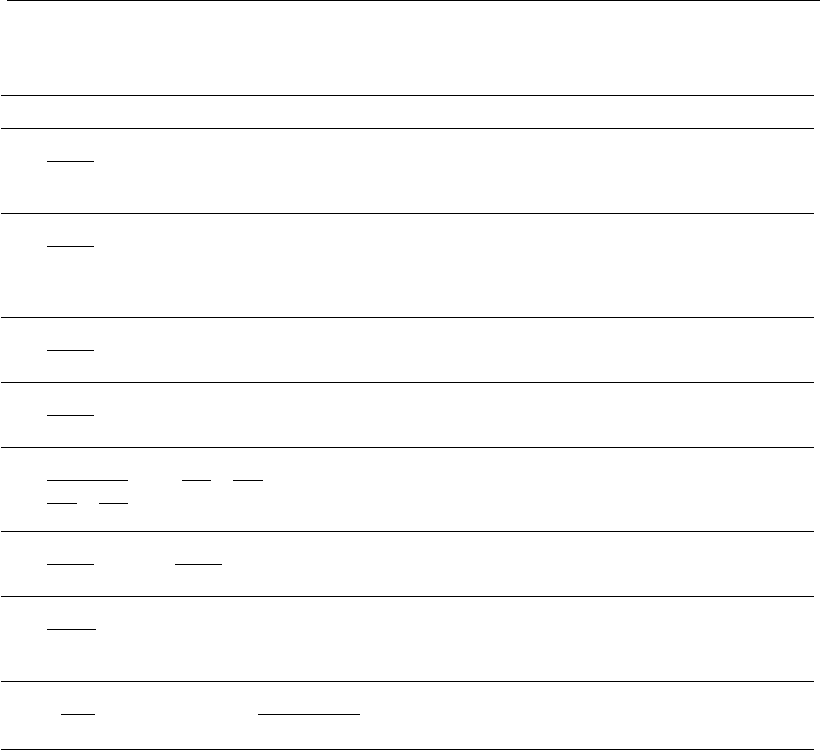
(proteins) synthesis. Once more, the diversity of mathematical structures

reﬂects the variability of response in such systems, as well as the lack of

knowledge of intracellular mechanisms.

Some models utilize the concept of Luedeking and Piret (1959) for

growth associated and/or non-growth associated production (Equations

65 to 67). However, in some circumstances, the best ﬁt occurs when the

speciﬁc death rate k

is considered, instead of the speciﬁc growth rate 

(Equations 68, 70 and 71) (Linardos et al., 1991; Zeng, 1996a, 1996b). This

statement follows the observation that antibody production increases

when cells are under conditions of stress.

Considering the inﬂuence of media components on speciﬁc production

rate, only one expression makes serum relevant (Equation 69), while

glutamine appears as a limiting substrate in three formulas (Equations 69

to 71), always with a Monod-type structure. Glucose shows either an

inhibitory effect over production (Equations 71 and 72), or a limiting and

inhibitory pattern simultaneously (Equations 70). Instead of the classical

Table 8.5 Kinetic parameters for speciﬁc uptake rates in hybridoma systems: equations are

valid for both substrates – GLC and GLN

Formulations References Eq.



max

X=S

)

 

de Tremblay et al., 1992;

Hiller et al., 1991

(57)



max

X=S

)

 

þ m

Harigae et al., 1994; Hiller et al.,

1991; Miller et al., 1988;

Kurokawa et al., 1994

(58)*



max

X=S

)

 

þ m

 e

Linardos et al., 1991 (59)



max

X=S

)

 (

 

min

) Frame and Hu, 1991a (60)



X=S



P=S

 

P=S



X=S

 

X,min

Frame and Hu, 1991b (61)



max

X=S

)

 

þ m

þ S

de Tremblay et al., 1992 (62)



 S

þ S

Po¨rtner et al., 1996;

Gaertner and Dhurjati, 1993

(63)



max

 

þ m

þ ˜



S þ (X

 k

)

Zeng, 1996a (64)

*Same formulation proposed in Equation 26.

Mathematical models for growth and product synthesis in animal cell culture 205

Table 8.6 Fitted parameters for models of Ta ble 8.5

Eq. References S Y

max

X=S

(10

cel/mmol)

(10

–10

mmol/cel.h)

Other parameters

(57) de Tremblay et al., 1992 GLN 3.80 – –

(58) Hiller et al., 1991 GLC 1.02 –

Miller et al., 1988 GLC 2.8 0.50 –

Harigae et al., 1994 GLC 5.88 0.51 –

GLN 3.44 0.08 –

Hiller et al., 1991 GLN 16.9 1.56

(59) Linardos et al., 1991 GLC 5.93 1.96 –

GLN 6.30 0.29 –

(60) Frame and Hu, 1991a GLC 0.355 mg cel/mg GLC

(p/,0.0508 h

–1

0.101 mg cel/mg GLC

(p/.0.0508 h

–1

)

p/,0.0508 h

–1



min

¼ 0.00630 h

–1

p/.0.0508 h

–1



min

¼ 0.391 h

–1

(61) Frame and Hu, 1991b GLC

1.82

(p/,0.00429 h

–1

)

0.52

(p/.0.00429 h

–1

)

–

¼ 0.00672 mg/cel.h;

º ¼ 9.31.10

–9

mg/cel;



X,min

¼ 0.013 h

–1

;

P=S

¼ 73.4 mg/mM

(62) de Tremblay et al., 1992 GLC 1.09 0.00708 k

¼ 1.0 mM

(63) Po¨rtner et al., 1996 GLN – –

¼ 0.68 10

–10

mmol/cel.h

¼ 0.2 mmol

Gaertner and Dhurjati, 1993 GLC – –

¼ 2.70 10

–10

mmol/cel.h

¼ 0.34 mmol

(64) Zeng, 1996a GLC 1.72 0.086

˜

GLC

¼ 0.094 L/10

cel.h

GLC

¼ 0.29 g/cel

GLN 9.52 0.0093

˜

GLN

¼ 0.033 L/10

cel.h

GLN

¼ 0.089 g/cel

206 Animal Cell Technology

formulation for the limitation or inhibition of a substrate (Equations 21

and 22), a hyperbolic structure is employed to represent inhibition, and

the parameter GLC



is introduced to represent the minimum glucose

concentration that guarantees product synthesis.

In Equation 70, Zeng (1996b) considers also the loss of production

capacity within the cell population – in the term (F

þ e

F

˜t

). This is a

characteristic common to many hybridomas that are expressed in long-

term culture. For Zeng (1996b), any cell population has two categories of

individuals, one characterized with high protein productivity, and another

with low protein productivity. The loss of producing capacity is attributed

to mutation or loss of genetic materials, and is irreversible. The parameter

‘‘F

’’ in Equation 70 represents the transformation rate from a producing

to a non-producing population. The parameter ‘‘F

’’ states a relationship

between the speciﬁc production rates of these two populations, each one

of them homogeneous in its productivity. Finally, an exponential function

–e

F

˜t

– simulates the loss of producing capacity within a cell popu-

lation.

If a process is operated in perfusion with high cell densities, Equation 70

might need an adjustment, as indicated in Equations 71 and 72. This can

occur by taking the relation (S=X

) for the main state variable, which

Table 8.7 Kinetic expressions for speciﬁc monoclonal synthesis rate

Formulations References Eq.



MAb

¼  Po¨rtner et al., 1996;

Hiller et al., 1991

(65)



MAb

¼ Æ  

þ  Frame and Hu, 1991b (66)



MAb



þ 

 

þ  de Tremblay et al., 1992 (67)



MAb

¼ Æ

 k

þ 

Linardos et al., 1991 (68)



MAb

¼ 

 (Serum)

GLN

MAb

GLN

þ GLN

Dalili et al., 1990 (69)



MAb

¼ (Æ

 k

þ 

)

GLN

MAb

GLN

þ GLN



Mab

i,GLC

GLC  GLC



þ k

MAb

i,GLC

þ e

F

˜t

) Zeng, 1996b (70)



MAb

¼ (Æ

 k

þ 

) 

GLN

MAb#

GLN

 X

þ GLN



MAb#

i,GLC

 N

GLC þ k

MAb#

i,GLC

 X

Zeng, 1996a (71)



MAb

¼  

Per

þ k

MAb

Per



MAb

i,GLC

GLC þ k

MAb

i,GLC

Zeng, 1996a (72)

Per

¼ speciﬁc perfusion rate (h

1

Mathematical models for growth and product synthesis in animal cell culture 207

includes the inﬂuence of substrate and high cell density (Equation 71); or

by considering the stimulation of productivity caused by the speciﬁc

perfusion rate (D

Per

Tables 8.9 and 8.10 show examples of kinetic expressions for byproduct

synthesis and the parameter values ﬁtted to them.

Frequently, the speciﬁc byproduct formation rate is presented as a

function of speciﬁc substrate consumption rate and substrate-to-product

yield (see Equation 12), but other structures can be assumed. The speciﬁc

production rate can be limited by a precursor substrate and modeled by a

Monod-type expression, as in Equation 73, or it may be inhibited by a

substrate that is not, in principle, linked to its production, as in Equation

Table 8.8 Fitted parameters for models of Table 8.7

Eq. References Æ

(mg/mg

cel

)



(mg/10

cel.h)

Other parameters

(65) Po¨rtner et al., 1996 – 0.0167 –

Hiller et al., 1991 – 0.708 –

(66) Frame and Hu, 1991b –0.0266 0.00672

(mg/mg

cel

.h)

–

(67) de Tremblay et al., 1992 0.146

¼ 0.115 mg/10

cel



¼ 8.33.10

–4

–1

(68) Linardos et al., 1991 – –

¼ 273 g/10

cel



¼ 0.0375 g/10

cel.h

(69) Dalili et al., 1990 – –



¼ 0.4 mg/10

cel.h

MAb

GLN

¼ 0.1 mM

(70) Zeng, 1996b – –

¼ 0 – 51.6 g/10

cel



¼ 0.5 – 1.21 mg/10

cel.h

MAb

GLN

¼ 4.42 – 9.01 mM

MAb

i,GLC

¼ 4.42 – 9.01 mM

GLC* ¼ 0.1 mM

¼ 0.37 – 1.18

¼ 0 – 0.018 h

–1

(71) Zeng, 1996a

¼ 0.092 mg/10

cel



¼ 1.33 mg/10

cel.h

MAb#

GLN

¼ 0.0079 mmol/10

cel

MAb#

i,GLC

¼ 12.65 mmol/10

cel

(72) Zeng, 1996a

¼ 4.16 mg/10

cel.h

MAb

Per

¼ 0.115 h

–1

MAb

i,GLC

¼ 13.97 mM

208 Animal Cell Technology

76 and 77. For example, glucose inhibits ammonia synthesis, an assump-

tion that takes account of the complex regulation of dual-substrate

metabolism (GLC and GLN) in animal cell systems (see Chapter 4).

In Equations 74 and 78 data ﬁt to a model that considers the concept of

excess substrate in culture, as set previously in Equation 36 (Zeng, 1995).

However, this formulation needs modiﬁcation in order to include high cell

density conditions. In Equations 75 and 79, as seen before, the mass of

nutrient available per cell (S=X

) is the state variable to take this into

account.

8.3.3 Parameter ﬁtting in models

Unstructured models, as detailed in Sections 8.3.1 and 8.3.2, are formu-

lated by a series of kinetic and differential non-linear equations that

represent the dynamics of all the state variables during the process. Thus,

to simulate a model that consists of parameters and state variables, it is

necessary to attribute values to the parameters.

The initial parameters values can be estimated in different ways:

(i) from the stoichiometric relationship, utilizing experimental or theor-

etical data;

Table 8.9 Kinetic formulations for synthesis of byproducts (ammonia and lactate)

Formulations References Eq.



LAC

¼ 

LAC,max



GLC

LAC

GLC

þ GLC

Gaertner and Dhurjati, 1993 (73)



LAC

¼ Y

LAC=X

 

þ m

LAC

þ ˜

max

LAC, GLC



GLC  GLC



GLC  GLC



þ k

LAC

GLC

Zeng, 1995 (74)



LAC

¼ Y

LAC=X

 

þ m

LAC

þ ˜

max

LAC, GLC



GLC

GLC þ k

LAC#

GLC

 X

þ ... Zeng, 1996a (75)

...þ ˜

max

LAC, GLN



GLN

GLN þ k

LAC#

GLN

 X



þ E

 GLC

þ GLC

Gaertner and Dhurjati, 1993 (76)



þ G

 LAC

þ LAC

Gaertner and Dhurjati, 1993 (77)



¼ Y

 

þ m

þ ˜

max

, GLN



GLN3

GLN3 þ k

GLN

þ ... Zeng, 1995 (78)

... þ˜

max

, GLC



GLC

GLC þ k

GLC



¼ Y

 

þ m

þ ˜

max

, GLN



GLN

GLN þ k

GLN

 X

Zeng, 1996a (79)

Mathematical models for growth and product synthesis in animal cell culture 209

(ii) by linearization and, sometimes, simpliﬁcation of kinetic equations

and by ﬁtting the experimental data by linear regression;

(iii) by utilizing parameter values available in the literature.

Item (i) above is largely employed to obtain substrate-to-cell and

substrate-to-product yield factors. When the substrate consumption is

diverted to several different products, an estimate of the substrate-to-

product yield factors can be based on the stoichiometric relationships

obtained from the biochemical reactions.

Table 8.10 Fitted parameters for models of Table 8.9

Eq. Byproducts

(bP)

bP=X



mmol

cel



mmol

cel  h



˜

max

bP,S

mmol

cel  h:



(mM)

Other parameters

(73) LAC 0.34



LAC,max

¼ 2.7

(mmol/10

cel.h)

(74) LAC 10,42 0.050 0.355 0.43

(75) LAC 2553 888 1322 (S ¼ GLN)

3663 (S ¼ GLC)

LAC#

GLN

0.013

(mmol/10

cel)

LAC#

GLC

¼ 17.54

(mmol/10

cel)

(76) NH

¼ 2.0

(mmol

/10

cel.L.h)

¼ 0.35

(mmol/10

cel.h)

¼ 3.3 mM

(77) NH

¼ 6.2

(mmol

/10

cel.L.h)

¼ 0.22

(mmol/10

cel.h)

¼ 14 mM

(78) NH

0.21 0.00068 0.032 (p/S ¼ GLN)

0.0041 (p/S ¼ GLC)

0.56

(p/GLN)

0.96

(p/GLC)

(79) NH

0.73 – 0.025 (S ¼ GLN)

GLN

0.071

(mmol/10

cel)

210 Animal Cell Technology

Item (ii) is largely employed in obtaining kinetic parameters such as the

substrate limitation and inhibition constants for cellular growth and death

and k

i,S

, respectively) and substrate inhibition constants for production

i,S

); maximum speciﬁc growth and death rates (

X,max

and k

d,max

), as well

as the global yield factors (Y

X=S

and Y

P=S

), that may be associated or not to

the cellular growth.

Simpliﬁcation of the equations involves separating the parameters to be

estimated.

Besides the simpliﬁcation, a subset of data must be selected, from the

available data set, that is more adequate for the determination and ﬁtting

of the parameters.

Andrew’s kinetic model (Equation 21) (Andrews, 1968), for example,

relates the speciﬁc growth rate (

) with the substrate concentration S,

applying three parameters (

X,max

and k

i,S

The initial parameter estimations of 

X,max

and k

can be based on a

simpliﬁcation of Equation 21, by disregarding the inhibition term for the

substrate. Thus, Equation 21 becomes Equation 80.



¼ 

X,max

þ S

(80)

Re-arranging this equation results in its linearization.



X,max



X,max



(81)

Using data extracted from the test conducted with non-inhibiting

substrate concentrations, the construction of the graph 1=

a þ b  (1=S) allows a ﬁt of values for ‘‘a’’ and ‘‘b’’ and, from these, an

estimate of 

X,max

and k

(Equation 81).

An initial estimate for parameter k

i,S

can be obtained by the simpliﬁca-

tion of Equation 21, disregarding the limitation for the substrate term, S,

forming Equation 82:



¼ 

X,max

S þ

i,S

(82)

Re-arranging this equation results in its linearization:



X,max



X,max:

i,s

 S (83)

Using data extracted from the test conducted with inhibiting substrate

concentrations, the construction of the graph 1=

¼ a þ b  S allows a ﬁt

of values for ‘‘a’’ and ‘‘b’’, and, from these, an estimate of 

X,max

and k

i,S

(Equation 83). Others ways of estimating parameters can be found in

Bonomi and Schmidell (2001).

Once the initial values of the parameters are estimated, the model

becomes dependent only on the state variable. From now on, forecasts can

be made with the model and the results compared to the experimental data

for different culture conditions (model simulation). Thus, the quality of

Mathematical models for growth and product synthesis in animal cell culture 211