Castilho Leda R., Moraes Angela Maria (Ed.) Animal Cell Technology: From Biopharmaceuticals to Gene Therapy
Подождите немного. Документ загружается.


glutamine concentration is very low (Figure 8.2D), which can indicate a
limitation of this nutrient.
It may be necessary to verify if the lactate levels (2.2 g/L) and/or
ammonium (35 mg/L) reach inhibitory concentration values. It is neces-
sary to consider the possibility of the occurrence of limitation and
inhibitory effects quite frequently in the culture. To discriminate between
the influences of several phenomena it is necessary to do tests under
conditions specifically planned for this purpose, allowing the investigator
to distinguish between limitation and inhibition phenomena.
The rate of change of
X
at the decline phase can also help in phenomena
identification. For example, an abrupt fall in the
X
value is an indication
of nutrient limitation. Once the limiting nutrient has reached a critical
concentration, complete depletion and a decrease in growth will occur
quickly. On the other hand, when a reduction of
X
occurs slowly, the
phenomenon responsible is usually the formation of an inhibiting metabo-
lite, which has gradually accumulated in the system.
There are other ways to identify the factors that regulate cell metabo-
lism, and each researcher may establish suitable methods for a particular
system based on kinetic data analysis (Sinclair and Kristiansen, 1987;
Engasser et al., 1998; Bonomi and Schmidell, 2001). Nevertheless, the
importance of adequate experimental data treatment is evident. This would
allow precise specific rate calculations and identification of the associated
phenomena.
8.3 Unstructured and non-segregated models
As stated previously, unstructured and non-segregated models are those
most commonly employed for simulating cell culture, due to their simpli-
city in representing the biological complexity of the system. It is should be
restated that these models consider the cell population as homogeneous
and do not distinguish between individual cells.
In this section, a classical set of equations – initially developed for
microbial systems – will be presented, followed by a review of the most
important models for cell culture in the literature.
8.3.1 Classical formulas for cell growth, substrate consumption, and
product synthesis
From kinetics studies of unicellular organisms, a set of mathematical
expressions have been established to represent the most frequent phenom-
ena in bioprocesses. These phenomena involve a limitation or inhibition of
growth and product formation, caused by the presence of substrates,
products, or byproducts in culture media. Many of these expressions do
not derive from known kinetic mechanisms. In fact, they are simply
mathematical expressions with fitted parameters that are able to reproduce
experimentally observed kinetic profiles. These equations have been
derived and used in many unstructured microbial or cell models.
192 Animal Cell Technology

Cell growth
Substrate limitation
Many of the equations employed in unstructured and non-segregated
models derive from those of enzymatic kinetics (Sinclair and Kristiansen,
1987; Nielsen and Nikolajsen, 1988). Cells are considered as chemical
reactors that support thousands of complex reactions catalyzed by en-
zymes that allow the conversion of substrates into secreted products. The
equation formulated by Michaelis and Menten represents the enzymatic
conversion rate of a unique substrate into one product (Equation 14).
r
E
¼ k E
S
k
m
þ S
(14)
where:
r
E
¼ reaction rate;
k ¼ reaction constant;
E ¼ enzyme total amount;
k
m
¼ Michaelis constant;
S ¼ limiting substrate concentration.
The amount (k.E) is the maximum reaction rate (r
E,max
), that always
occurs at conditions where limiting substrate concentrations are much
higher than the constant k
m
(S ..k
m
), allowing enzyme saturation by
substrate.
By analogy to Michaelis and Menten enzymatic kinetics, Monod (1949)
proposed the formula shown in Equation 15 that represents the cell
growth rate as a function of cell and substrate concentrations.
r
X
¼
X,max
S
k
S
þ S
X (15)
where:
X,max
¼ maximum specific cell growth rate (T
1
);
k
S
¼ substrate limitation constant for growth (or substrate saturation
constant for growth) (M L
3
);
S ¼ limiting substrate concentration (M L
3
);
X ¼ cell concentration (M L
3
or Cel L
3
).
This same equation can be written as a function of the specific growth
rate (Equation 16).
X
¼
X,max
S
k
S
þ S
(Monod, 1949) (16)
Thus, the specific growth rate can be expressed by two parameters
(constants) –
X,max
and k
S
– and one state variable – S. This allows a
parameter fitting to experimental data of cell (X) and substrate (S)
concentrations. The procedure to fit these parameters will be shown in
Section 8.3.3.
Figure 8.4 presents simulations of the Monod model with different sets
of parameters. As a general rule, whenever the limiting substrate is in
excess (S ..k
S
), specific cell growth takes the maximum value (
X,max
),
and becomes independent of substrate.
Mathematical models for growth and product synthesis in animal cell culture 193
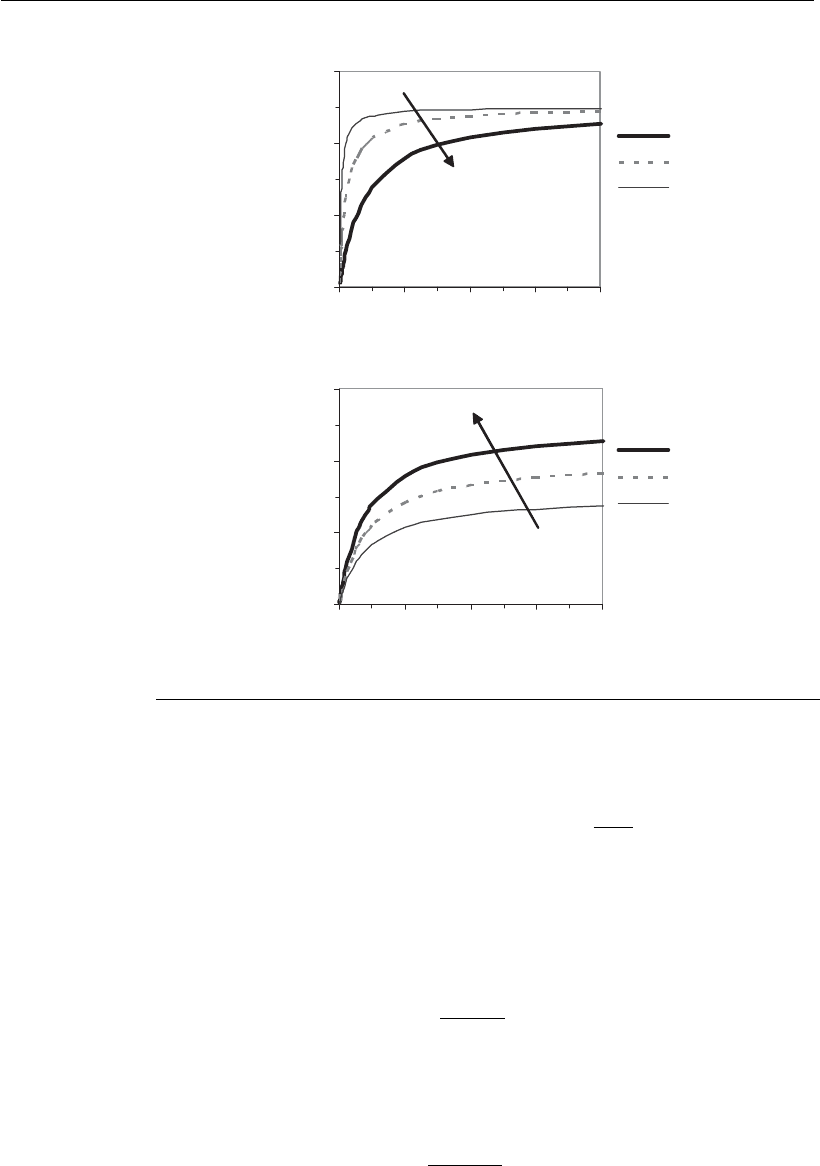
When the limiting substrate reaches the concentration equivalent to k
S
,
the specific growth rate assumes the value of
X,max
2
. This is the critical
substrate concentration for cell growth.
Certainly, Monod’s formula has been used extensively in phenomenolo-
gical (unstructured) models, although the literature presents other equa-
tions for one limiting substrate systems (Equations 17 and 18). In Moser’s
formulation it was necessary to introduce a third parameter (‘‘n’’ in
Equation 17) to represent experimental data.
X
¼
X,max
S
n
k9
S
þ S
n
(Moser, 1958) (17)
where:
k9
S
¼ constant ((M L
3
)
2
)
X
¼
X,max
S
k0
S
X þ S
(Contois, 1959) (18)
0.00
0.02
0.04
0.06
S (g/L)
S (g/L)
0.80
0.20
0.05
k
S
k (g/L)
S
(a)
k 0.8 g/L
S
⫽
0.00
0.02
0.04
0.06
0.05
0.04
0.03
µ
X, MAX
(b)
µ
X
1
(h )
⫺
µ
X
1
(h )
⫺
µ
X,MAX
1
0.05 h⫽
⫺
0
0
2
2
4
4
6
6
8
8
µ
X,max
1
(h )
⫺
Figure 8.4
Specific growth rate as a function of limiting-substrate S, for different sets of
parameters
X,max
and k
S
.
194 Animal Cell Technology

where:
k 0
S
¼ constant (M M
1
or M Cel
1
)
Equation 19 presents a kinetic model for dual-limiting substrates (S
1
and S
2
) in culture. In such cases, the Monod structures for substrate
limitation (
S
i
k
S
i
þS
i
) are reproduced for each one of the limiting substrates.
X
¼
X,max
S
1
k
S
1
þ S
1
:
S
2
k
S
2
þ S
2
(Megee et al:, 1972) (19)
The proposal made by Megee et al. (1972) is valid whenever limiting
substrates are consumed simultaneously and both are essential for growth.
This means that growth is interrupted when complete consumption of any
substrate occurs, even though the other substrate is in excess. Dunn et al.
(1992) proposed the idea of enhancing substrates that are non-essential,
but if available they can improve specific cell growth rate (Equation 20).
X
¼
X,max1
S
1
k
S
1
þ S
1
þ
X,max2
S
2
k
S
2
þ S
2
(Dunn et al:, 1992) (20)
Substrate inhibition
Models formulated in Equations 21 and 22 describe the situation of a
medium component that can be either a limiting substrate or an inhibiting
substrate. At the beginning of a culture, the high substrate concentration
causes growth inhibition; nevertheless the gradual consumption by cells
reduces this effect until concentration gets low enough to become limiting.
X
¼
X,max
S
k
S
þ S þ
S
2
k
i,S
(Andrews, 1968) (21)
where:
k
i,S
¼ substrate inhibition constant for growth (M L
3
).
X
¼
X,max
S
1 þ
k
S
S
þ
S
k9
i,S
n
(Wu et al:, 1988) (22)
where:
k9
i,S
¼ constant ((M L
3
)
n
).
Product inhibition
Equations 23 to 25 are expressions of growth inhibition due to synthesis
of byproducts during culture. Those formulas can represent exponential,
hyperbolic, and linear reduction profiles of specific growth rates as a
function of product accumulation in the culture environment.
X
¼
X,max
e
k9
i,P
P
(Aiba et al:, 1968) (23)
where:
k9
i:P
¼ product inhibition constant for growth (L
3
M
1
).
Mathematical models for growth and product synthesis in animal cell culture 195

X
¼
X,max
k
i,p
k
i,P
þ P
(Aiba and Shoda, 1969) (24)
where:
k
i,P
¼ product inhibition constant for growth (M L
3
).
X
¼
X,max
1
P
P
m
(Ghose and Tyagi, 1979) (25)
where:
P
m
¼ maximum product concentration that states for
X
¼ 0(M L
3
).
Substrate consumption
The classical studies of Monod (1942) demonstrated a carbon flux partition
between catabolism and anabolism, and suggested that a small amount of
the carbon uptake is used for maintenance purposes. However, at that time
it was impossible to determine the consumption needed for cell main-
tenance, because the methodologies lacked precision.
Later, it was observed that substrate to cell yield factors (Y
X=S
) could
vary as a function of specific growth rate. Pirt (1966) described a linear
relationship between growth and substrate consumption, as well as the
statement of a term for cell maintenance (Equation 26).
S
¼
1
(Y
max
X=S
)
X
þ m
S
(Pirt, 1966) (26)
where:
m
S
¼ specific substrate uptake rate for maintenance, or maintenance
coefficient (M M
1
T
1
or M Cel
1
T
1
);
Y
max
X=S
¼ maximum or global substrate-to-cells yield factor (M M
1
or
Cel M
1
).
This expression establishes a variation of the real yield factor as a
function of specific growth rate (Equation 27).
1
Y
X=S
¼
1
Y
max
x=s
!
þ
m
S
X
(27)
The maintenance coefficient can explain the non-growth associated
substrate consumption for energy production, an energy that supports
transmembrane ions gradient, motility, among other functions.
The expression established by Pirt (1966) describes anaerobic systems
and carbon-limited cultures. However, it gives a poor representation under
substrate excess (Zeng and Deckwer, 1995a, 1995b). Then, Tsai and Lee
(1990) built a model to represent the excessive consumption of substrate,
under conditions of substrate excess (Equation 28).
S
¼
S
þ
E
S
(Tsai and Lee, 1990) (28)
where:
S
¼ specific substrate uptake rate under substrate limitation conditions
196 Animal Cell Technology

(M M
1
T
1
or M Cel
1
T
1
);
E
S
¼ increment or decline of specific substrate uptake rate due to
substrate excess (M M
1
T
1
or M Cel
1
T
1
).
Zeng and Deckwer (1995a, 1995b) demonstrated the flexibility of the
Tsai and Lee (1990) proposition in representing data from microorganisms
and animal cells, using the following equations to describe the terms
S
and
E
S
:
S
¼
X
Y
max
S
þ m
S
(with S , S
) (Zeng and Deckwer, 1995a) (29)
E
S
¼ ˜
max
S
S S
S S
þ k
S
S
(with S > S
) (Zeng and Deckwer, 1995a)
(30)
where:
˜
max
S
¼ maximum increment or decline of specific substrate uptake
rate due to substrate excess (M M
1
T
1
or M Cel
1
T
1
);
S
¼ substrate concentration under substrate limitation (M L
3
);
(S S
) ¼ excess of substrate (M L
3
);
k
S
S
¼ substrate limitation constant for substrate uptake (M L
3
).
Product formation
Similarly to cell growth, the literature presents a set of expressions relating
specific product synthesis and state variables (Bonomi and Schmidell,
2001).
Equation 31 shows the generic model for product synthesis formulated
by Luedeking and Piret (1959). In this model, the product synthesis can be
associated to growth (term Æ
X
), and also in a non-associated form (). In
many situations only one of the phenomena is observed – the synthesis is
associated or non-associated – employing only one of the terms of Equa-
tion 31. Figure 8.5 illustrates the kinetics profiles for the three different
possibilities of product synthesis described above.
P
¼ Æ
X
þ (Luedeking and Piret, 1959) (31)
where:
Æ ¼ constant for growth-associated production (M M
1
or M Cel
1
);
¼ constant for non-growth-associated production (M M
1
T
1
or
M Cel
1
T
1
).
A usual modification for this equation considers the influence of
substrate concentration on the non-associated term, usually expressed as a
Monod-type limitation (Equation 32).
P
¼ Æ
X
þ
m
S
k
p
S
þ S
(32)
where:
m
¼ constant (M M
1
T
1
or M Cel
1
T
1
);
k
p
S
¼ substrate limitation constant for product synthesis (M L
3
).
Mathematical models for growth and product synthesis in animal cell culture 197
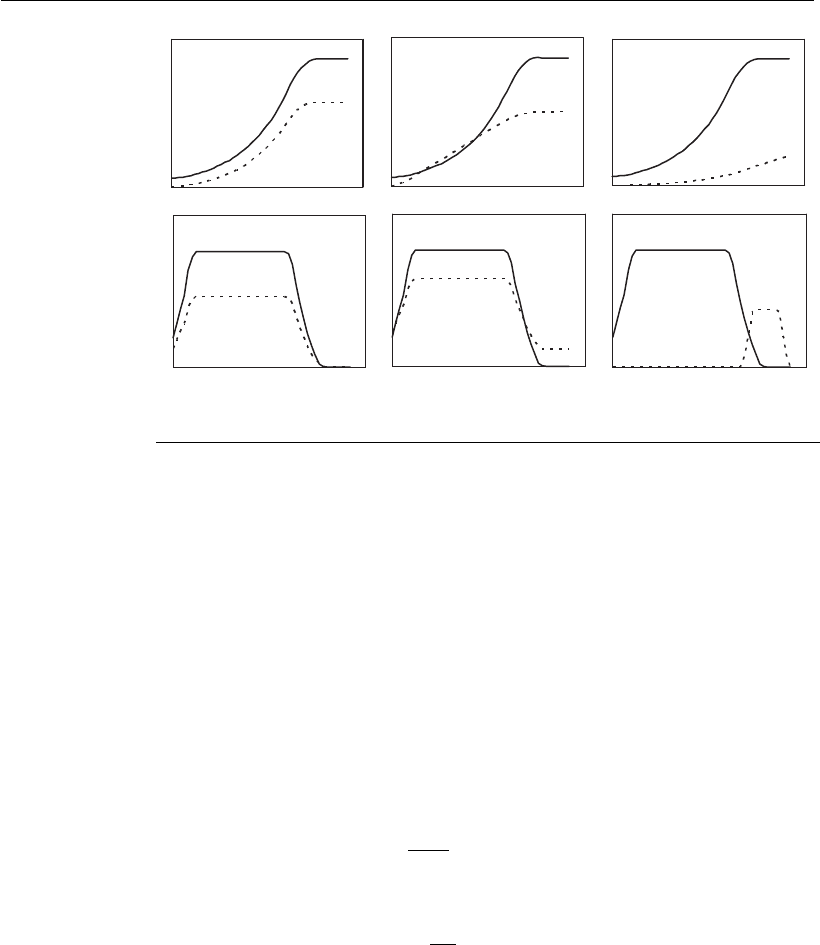
Another form of inhibition of product synthesis results from the
product accumulation in the medium itself, that can be modeled using the
same structures seen before (Equations 23 to 25) for cell growth inhibition
(Equations 33 to 35).
P
¼
P,max
e
k
P9
i,P
P
(Aiba et al:, 1968) (33)
where:
P,max
¼ maximum specific product synthesis rate (M M
1
T
1
or
M Cel
1
T
1
);
k
P9
i,P
¼ product inhibition constant for product synthesis (L
3
M
1
).
P
¼
P,max
k
P
i,P
k
P
i,P
þP
(Aiba and Shoda , 1969 ) (34)
k
P
i,P
¼ product inhibition constant for product synthesis (M: L
3
).
P
¼
P,max
1
P
P9
m
(Ghose and Thiagi, 1979) (35)
where:
P9
m
¼ maximum product concentration that determines
P
¼ 0
(M L
3
).
Similarly to what was seen in Equations 28 to 30, Zeng (1995) and Zeng
and Deckwer (1995a) proposed a model for specific production rate
considering three aspects: production associated with growth; production
not associated with growth, and a term due to substrate excess that causes
an increment or decline of the specific production rate (Equation 36).
X
P
(A) X
P
(B)
X
P
(C)
Time (h) Time (h) Time (h)
µ
X
µ
X
µ
X
µ
P
µ
P
µ
P
Figure 8.5
Profile for growth and product synthesis according to different production models:
(A) growth associated production; B) growth partially associated production, and;
C) non-growth associated production.
198 Animal Cell Technology

P
¼ Y
P=X
3
X
þ m
P
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Limitation of Substrate
þ ˜
max
P
S-S
P
S-S
P
þ k
P
S
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Excess of Substrate
(Zeng, 1995; Zeng and Deckwer, 1995a)
(36)
where:
Y
P=X
X
¼ growth-associated specific production rate, under sub-
strate-limiting conditions;
Y
P=X
¼ yield coefficient for product formation due to cell growth
(M M
1
or M Cel
1
);
m
P
¼ nongrowth-associated specific production rate, under substrate-
limiting conditions (M M
1
T
1
or M Cel
1
T
1
);
˜
max
P
SS
P
SS
Pi
þk
P
S
¼ increment or decline of specific production rate due to
substrate excess;
˜
max
P
¼ maximum increment or decline of specific production rate due
to substrate excess (M M
1
T
1
or M Cel
1
T
1
);
S
P
¼ substrate concentration at which an increase or decrease of
P
starts to take place (M L
3
);
(S S
P
) ¼ substrate excess for product synthesis (M L
3
);
k
P
S
¼ substrate limitation constant for product synthesis (M L
3
).
8.3.2 Kinetic models for animal cells
In the previous section, the main equations used for building unstructured
and non-segregated generic models were discussed. In principle, the
description of an animal cell system can be based on any of these formulas,
or combinations of them, as can be seen in some literature reviews
(Tziampazis and Sambanis, 1994; Po
¨
rtner and Scha
¨
fer, 1996; Sidoli et al.,
2004). Nevertheless, the complexity of animal cell systems also demands
alternative mathematical expressions for the full description of observed
phenomena.
The identification of such phenomena, as the basis for any mathematical
model building, assumes certain knowledge about cell metabolism, under
different culture conditions. Chapter 4 discusses the metabolism of animal
cells, and should be consulted for a full understanding of the kinetic
models presented below.
Kinetics models for cell growth and death, as well as for substrate
consumption and product and byproduct synthesis, are presented here.
Most of these were developed for hybridomas in continuous processes.
Although these models are representative of animal cell systems, it is
important to understand that the cellular response to an environmental
stimulus is highly dependent on the specific cell line. The review
published by Po
¨
rter and Scha
¨
fer (1996) illustrated this variability through
the comparison of experimental data and models from different groups of
cell lines. Besides this, the lack of proper knowledge to explain experi-
mentally observed phenomena also accounts for the variability of model
structures.
Mathematical models for growth and product synthesis in animal cell culture 199
Kinetic formulations for animal cell growth
Table 8.1 summarizes a set of mathematical expressions for the description
of the specific growth rate during culture. Most of these formulations
employ Monod-type structures for cell growth limitation by substrates
(Monod, 1949), and structures for byproduct inhibition (Aiba and Shoda,
1969; see Equations 16 and 24).
Glucose and glutamine, which provide carbon for catabolic and anabolic
pathways, appear in the majority of models as limiting substrates. Cer-
tainly, the frequency of glucose and glutamine as limiting substrate
indicates their importance to cell metabolism, but also the need for
Table 8.1 Kinetic equations for specific hybridoma growth rates
Formulations References Eq.
X
¼
X,max
GLN
k
GLN
þ GLN
Po¨rtner et al., 1996 (37)
X
¼
X,max
GLC
k
GLC
þ GLC
GLN
k
GLN
þ GLN
de Tremblay et al., 1992 (38)
X
¼
X,max
GLC
k
GLC
þ Glc
k
i,LAC
k
i,LAC
þ LAC
Kurokawa et al., 1994 (39)
X
¼
X,max
GLN
k
GLN
þ GLN
k
i,NH
3
k
i,NH
3
þ NH
3
k
i,LAC
k
i,LAC
þ LAC
Bree et al., 1988 (40)
X
¼
X,max
GLC
k
GLC
þ GLC
GLN
k
GLN
þ GLN
k
i,NH
3
k
i,NH
3
þ NH
3
k
i,LAC
k
i,LAC
þ LAC
Miller et al., 1988 (41)
X
¼
X,min
þ (
X,max
X,min
)
(GLC GLC
thres
)
k
GLC
þ (GLC GLC
thres
)
Frame and Hu, 1991a (42)
X
¼
X,max
(Serum)
GLC
k
GLC
þ GLC
Dalili et al., 1990 (43)
X
¼
X,max
Serum
(Serum þ (k
Serum
)
0
X
)
GLN
k
GLN
þ GLN
:
k9
i,NH
3
k9
i,NH
3
þ (NH
3
)
2
Glacken et al., 1989 (44)
X
¼ a
1
B a
2
B
Gaertner and Dhurjati,
1993
(45)
X
¼ D þ d
0
e
(d
1
=
X
)
Linardos et al., 1991 (46)
X
¼
X,max
1 Æ
1
X
V
D
GLC
k
GLC
þ GLC
GLN
k
GLN
þ GLN
Zeng et al., 1998 (47)
Adapted from Po¨rtner and Scha¨fer, 1996. GLC, glucose; GLN, glutamine; NH
3
, ammonia; LAC, lactate; B, base
medium concentration; D, specific feed rate; Xv, concentration measured as viable cells number per volume
(10
6
cell/ml).
200 Animal Cell Technology

facilities to determine these substances in comparison to other media
components. Nevertheless, not all formulas indicate dual limiting-
substrate kinetics (GLC and GLN), mainly because the cell response
depends upon the cell line and on the culture conditions.
It is possible to represent a kinetic limitation by introducing a threshold
concentration, as GLC
thres
in Equation 42 (Frame and Hu, 1991a). This
parameter suggests the existence of an unknown component in culture
medium, which causes growth limitation when the glucose concentration
reaches the value GLC
thres
.
Zeng et al. (1998) proposed another way to deal with unknown limiting
or inhibiting components. From an evaluation of growth, death, and
production kinetics of hybridomas in perfusion culture, they noted that
neither glucose and glutamine limitation, nor lactate and ammonia inhibi-
tion, the most frequent phenomena in an unstructured model, could
explain their data. The introduction of parameter Æ
1
(Equation 47), which
relates the specific autoinhibitor production rate and its critical concentra-
tion, could represent the behavior of many different cell lines. However,
this model shows a strong dependence on the substrate availability,
represented by the specific feed rate (D), as well as on viable cell
concentration (X
V
). This alternative model shows the difficulty, still
present, in establishing a cause–effect relationship between a change in the
environment and cell behavior.
Gaertner and Dhurjati (1993) used the initial concentration of base
medium (B) in an attempt to handle the absence of information concerning
the limiting substrate (Equation 45). The base medium corresponded to a
DMEM formulation without GLC, GLN, NaCl, and NaHCO
3:
Different
concentrations of this base were tested. The solution showed a hyperbolic
relationship between the specific growth rate and the basal medium
concentration, independently of the effective limiting component.
Finally, Equations 43 and 44 introduce serum concentration, measured
as a percentage of total volume, as the growth-limiting factor. Except for
the work of Kurokawa et al. (1994), all models presented in Table 8.1
derive from data obtained in serum-based cultures. However, only two of
these models (Glacken et al., 1989; Dalili et al., 1990) utilize this strategy
to represent the unknown limiting component.
In general, glucose and glutamine are consumed at a high rate, since cells
in culture cannot regulate their uptake. Therefore, cells synthesize large
amounts of lactate and ammonia, eventually accompanied by amino acids
secretion (alanine, glycine, and aspartate). This absence of regulation
causes the rapid depletion of substrates (GLC and GLN) from media, and
the consequent accumulation of byproducts (LAC and NH
3
), potential
inhibitors of the system, both represented in Equations 39 to 41 and 44.
Among the possibilities presented in Section 8.3.1 (Equations 23 to 25),
the structure for a hyperbolic inhibitory profile is the most widely used
(see Equations 39 to 41, 44 and 47). However, not every formula includes
an expression for the potential inhibition of byproducts (LAC and NH
3
),
since the response is cell-dependent.
The values of the parameters shown in Table 8.1, used in building of
models, were fitted from different sets of experimental data. Except for
very robust models that can represent a large number of situations, differ-
Mathematical models for growth and product synthesis in animal cell culture 201
