Castilho Leda R., Moraes Angela Maria (Ed.) Animal Cell Technology: From Biopharmaceuticals to Gene Therapy

Подождите немного. Документ загружается.

there is an urgent need to increase bioprocess efﬁciency and productivity.

The reduction of cost is essential to insure that animal cell culture remains

competitive compared to alternative technologies such as ribosome display

and transgenic animals. Improvements can be made by a biological

approach, as discussed in Chapter 3, or based on the optimization of

culture conditions. Mathematical modeling is probably the most efﬁcient

technique for the optimization of culture conditions.

The construction of a mathematical model involves the following steps,

as developed by several authors (Engasser et al., 1998; Miller and Reddy,

1998; Bonomi and Schmidell, 2001).

(i) Formulation of kinetic equations. This is probably the most impor-

tant step in developing models because it establishes mathematical

relations between the observed phenomena and the cellular responses.

It depends on several tasks, namely:

– Deﬁnition of variables relevant to the process: state variables,

such as cells, substrates, and product concentrations, that

characterize the system studied; and operational variables, that

represent particular conditions of the system, that may be initial

or ﬁxed conditions such as initial concentrations, feeding rates,

etc.;

– Kinetic analysis of experimental data and proposed hypotheses of

the process limitations or inhibitory steps, which correspond to

the identiﬁcation of the dominant phenomena in the system;

– Selection of mathematical equations able to represent the speciﬁc

rates (for growth, product synthesis and substrate consumption)

that can describe the phenomena identiﬁed in the previous steps.

(ii) Establishment of mass balances, total and for each component, con-

sidering the operational and state variables. Examples of mass bal-

ances for different operation modes (batch, fed-batch, continuous,

etc.) are presented in Chapter 9. Depending on the deﬁned variables

in the model, it may be necessary to perform energy and momentum

balances.

(iii) Parameter ﬁtting. Mathematical model equations contain state vari-

ables and one or more parameters that are mathematical constants.

This step of model formulation, called parameter ﬁtting, consists in

deﬁning optimal values for these parameters that minimize the

discrepancies between experimental values and the values calculated

through the equations (simulated values).

(iv) Model validation. The applicability of a model comes from its

capacity to predict cell behavior under different culture conditions.

Thus, the procedure for model validation consists of comparative

statistical analysis between real values (experimental) and calculated

values (model simulation). This is an indispensable step to complete

the task of modeling any system.

The crucial step in model building is model formulation, since the

mathematical modeling is intended to represent a large network of multi-

ple biochemical reactions, controlled by complex regulatory processes that

182 Animal Cell Technology

cause cell adaptation to changes in culture conditions. The complexity of

cell metabolism may be treated by different approaches, and both the type

of information needed and the material resources to get it should be taken

into account when modeling.

The systematization of biological data through mathematical modeling

is not a trivial task and requires the intensive use of material and human

resources. Moreover, the models often incorporate experimental uncer-

tainties that do not always allow the identiﬁcation of the trends of the

culture, with the desired precision. Figure 8.1 summarizes the main types

of models applied to the description of cellular metabolism, according to

the classiﬁcation proposed by Tsuchiya et al., (1966).

Unstructured and non-segregated models allow the most simpliﬁed

representation of cellular complexity. As indicated in Figure 8.1, in these

models, the entire cell population is represented by only one kind of cell

(the average cell). Differences between cells within the population are not

considered and thus, the cell population is considered homogeneous.

Although an unstructured and non-segregated model includes simpliﬁ-

cations of the cellular complexity, it is often used in culture simulation,

because it is an adequate compromise between the available data, the

difﬁculties involved in model formulation, and the desired model preci-

sion.

The unstructured and segregated model considers the cell culture as a

heterogeneous population, with individual cells characterized by age,

mass, or size. The variation of properties follows a statistical distribution.

The most concise way to deal with such population heterogeneity is

through a population balance model (PBM). These models can become

mathematically complex because the equations that describe the popu-

lation have to consider that the properties vary in the population and

Balanced

cell

Unstructured Structured

Non-segregated

Segregated

One cell behaves like

others cells, the cell

and the population

are homegeneous

growth

(approximation)

The cell population is

described by one kind of

cell with many intracellular

components, an

heteregeneus cell.

Mean

(approx.)

Mean

(approx.)

The cell population has different

individuals, a heterogeneous

population, but the cell has

intracellular componentes

a homogeneous cell.

The cell is a representation of

acellular multicomponents

with different cell by cell.

intr

growth

(approx.)

Balanced

Figure 8.1

Model classiﬁcation (based on Tsuchiya et al., 1966; Bailey and Ollis, 1986).

Mathematical models for growth and product synthesis in animal cell culture 183

during the time course of cell culture. The mathematical description in a

segregated model is based on partial differential equations, while the non-

segregated model is described entirely by ordinary differential equations.

Although this complexity adds difﬁculties to the mathematical solution of

the problem, and also to the estimation of model parameters, new

mathematical tools and advances in process monitoring have made possi-

120

160

ALA (mg/L)

GLY (mg/L)

(F)

0.00

0.01

0.02

0.03

0.04

0.05

(E)

MAb ( g/mL)µ

(C)

200

400

600

GLN (mg/L)

NH (mg/L)

⫹

(D)

0.E 00⫹

5.E 05⫹

1.E 06⫹

2.E 06⫹

3.E 06⫹

Time (h)

X (cel/mL)

100

Viab (%)

(A)

GLC (g/L)

LAC (g/L)

(B)

X,App

(h )

⫺

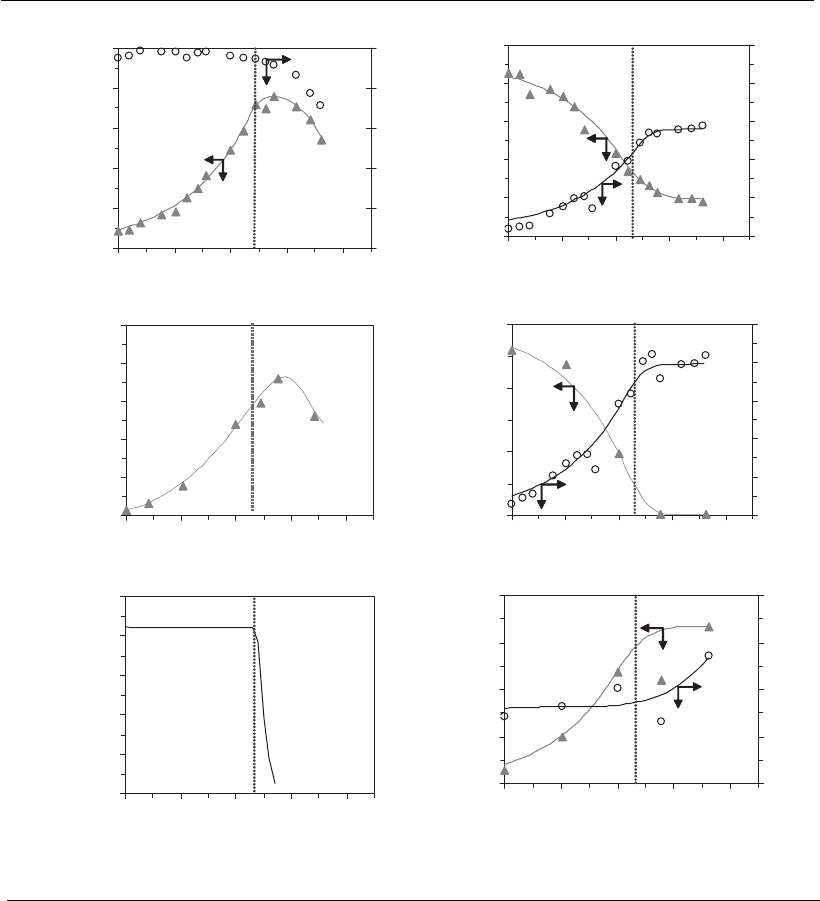
Figure 8.2

Typical kinetic proﬁles (hybridoma). (A) Cell concentration and viability; (B) glucose consum ption

(GLC) and lactate production (LAC); (C) monoclonal antibody produ ction (mAb); (D) glutamine

consumption (GLN) and ammonium production (NH

); (E) speciﬁc growth rate (

); (F) alanine

(ALA) and glycine (GLY) production. Adapted from Lee (2003). Symbols correspond to the

experimental data and the lines to the manual curve ﬁtting. Vertical lines indicate the instant at

which exponential growth phase ended (

, 

X,max

184 Animal Cell Technology

ble the use of such models, changing the past situation when these models

were restricted to academic research.

The structured and non-segregated model considers the cellular popu-

lation as homogeneous with reference to certain characteristics (age, size,

and mass), however the intracellular structures are discriminated, in such a

way that each cell represents a heterogeneous structure. Thus, it is possible

to characterize with more precision, the cellular state through the know-

ledge of the dynamics of these internal structures and its response to the

environment conditions. The main advantage of the use of these models is

an improved knowledge about the process and, consequently, the capacity

to predict cell adaptation to environmental changes. Certainly, increasing

the number of cell structures results in an increase of the number of

equations and parameters required to describe process dynamics. More-

over, intracellular measurements that require sophisticated methodologies

and equipment are necessary. In the past, the use of this type of model was

restricted to academic research, but in recent years, it has become more

feasible for use in process simulation and evaluation.

The structured and segregated model considers a heterogeneous cell

population and the cell as a heterogeneous structure, thus representing the

diversity of physiological states as well as intracellular structures and the

metabolic pathways associated with each structure. This type of model

represents the complexity occurring in cell culture. Although these models

aim to represent cell growth in a more realistic way, the complexity

involved in the mathematical formulation and in ﬁtting of the parameters

makes their applicability very restrictive.

Depending on the degree of complexity, these models can be very

difﬁcult to solve mathematically. Even with some simpliﬁcations, for

instance, separating the cells into discrete populations to avoid inﬁnite

equations that could be generated considering a continuous population

distribution, difﬁculties in determining the internal characteristic para-

meters may still remain.

The complexity involved in cell structured and segregated models is

increased with the necessity of their integration and can explain why some

authors deﬁne the structured and segregated models as the next challenge

for animal cell modeling. These difﬁculties are reﬂected by the scarce

number of publications dealing with this integration. This advanced

research ﬁeld is beyond the scope of this book.

The mathematical modeling of animal cell processes was reviewed by

Tziampazis and Sambanis (1994), Po

rtner and Scha

fer (1996), and Sidoli

et al., (2004). These authors focused on non-structured and non-segregated

models, certainly the most abundant models in literature, and also dis-

cussed the evolution of the use of other models, mainly the structured and

segregated ones.

8.2 Kinetic analysis of bioprocesses

When studying the kinetic behavior of a system, it is necessary to under-

stand how the concentrations of the representative components of the

system (cell, substrate, products, and byproducts) vary with time. Thus,

Mathematical models for growth and product synthesis in animal cell culture 185

the analysis of the change of these variables with time allows the calcula-

tion of some kinetic variables that characterize the system and are the basis

for the identiﬁcation of the controlling phenomena.

The mathematical modeling of animal cell processes has many elements

in common with the modeling of microbial systems. In fact, many

examples of mathematical modeling discussed in Section 8.3.1 were ini-

tially considered for microorganisms and were later adapted to animal

cells.

Figure 8.2 (see page 184) shows the typical behavior of animal cells in

culture. Cell growth, substrate consumption, and product synthesis pro-

ﬁles are very similar to those presented in Chapters 2, 4, and 9, and will be

used to demonstrate the approach to data treatment usually applied to this

kind of process.

Considering that animal cells have high nutritional requirements, the

culture medium is always a complex formulation to insure the adequate

function of catabolism and anabolism (see Chapters 4 and 5). Glucose and

glutamine are precursors for biosynthesis and energy generation pathways,

and are the most highly consumed substrates. In parallel, lactate and

ammonium are synthesized at high rates as byproducts of glucose and

glutamine (or other amino acid) metabolism, respectively. There is also the

possibility of secretion of amino acids (mainly alanine, glycine, and

aspartate) and of commercially attractive products (monoclonal anti-

bodies, mAbs, for example).

8.2.1 Characteristic kinetic variables

The identiﬁcation of phenomena that explain the behavior of a studied

system depends on the analysis of their kinetic data. Normally, this kinetic

analysis is performed using characteristic variables calculated from the

experimental data. The speciﬁc rates and the yield coefﬁcients are the

common values used in this task. When cell concentration data are avail-

able, cell growth and death rates, as well as cell viability, are the best

kinetic variables to characterize the population physiological state. In the

absence of this information – as can occur, for example, with immobilized

cells – the treatment must be based on substrate consumption or on

metabolites production (Miller and Reddy, 1998).

Speciﬁc rates

To predict kinetic behavior it is necessary to know the change of the state

variables over time. Thus, it is necessary to determine the characteristic

rates of the system under transformation. The instantaneous cell growth

rate, for example, is deﬁned in Equation 1.

(1)

where:

¼ viable cell concentration (M  L

3

or Cel  L

3

);

¼ cellular growth rate (M  L

3

 TorCel L

3

 T);

t ¼ time (T).

186 Animal Cell Technology

As indicated above, the units deﬁned for the listed variables are given in

the MLT system, except in cases where cell concentration (given for

animal cells as numbers) is involved. M represents mass, L length, and T

time.

Similar equations can be written for the substrate consumption rate (r

)

and product synthesis rate (r

¼

(2)

(3)

where:

¼ substrate consumption rate (M  L

3

 T

1

);

¼ product synthesis rate (M  L

3

 T

1

);

S ¼ substrate concentration (M  L

3

);

P ¼ product concentration (M  L

3

The instantaneous rates are necessary for the characterization of the

cellular activities but may not be sufﬁcient. This occurs because during a

speciﬁc interval of time, the concentration of cells can vary signiﬁcantly,

and this may affect transformation rates. Therefore the speciﬁc growth

rate is deﬁned as a characteristic rate of the population. The speciﬁc

growth rate is calculated from the cellular growth rate divided by the

cellular concentration, and can be represented by the Equation 4 (Miller

and Reddy, 1998; Hiss, 2001):





 r

ðÞ

(4)

where:



¼ speciﬁc growth rate (T

1

The speciﬁc growth rate can be calculated from cellular concentration

data if the cell viability is sufﬁciently high. When the cell death rate is

signiﬁcant, the value obtained from Equation 4 is in fact an ‘‘apparent’’

speciﬁc rate, since the measured values in the laboratory are determined as

a balance between growth and death. The apparent rate is related to the

true speciﬁc growth rate by the following equation:



¼ 

 k

(5)

where:



¼ apparent speciﬁc growth rate (T

1

);

¼ speciﬁc cell death rate (T

1

The speciﬁc death rate can be obtained directly from viable and dead

cell concentrations (Equation 6).



(6)

where:

¼ dead cell concentration (M  L

3

or Cel  L

3

Mathematical models for growth and product synthesis in animal cell culture 187

The methodology normally used for the determination of dead cell

concentrations is the dye exclusion method (Freshney, 1994), although this

is not adequate in cases in which cellular lysis is signiﬁcant. In these

situations, other methodologies must be adopted to determine the amount

of lysed cells, such as, for example, the measure of the lactate dehydrogen-

ase concentration (LDH) in the culture medium (Freshney, 1994; Miller

and Reddy, 1998).

It is possible deﬁne the speciﬁc substrate consumption rate (Equation 7)

and speciﬁc product synthesis rates (Equation 8) in a similar way to the

speciﬁc growth rate.







 (r

) (7)

where:



¼ speciﬁc substrate consumption rate

(M  M

1

 T

1

or M  Cel

1

 T

1

);





 r

ðÞ

(8)

where:



¼ speciﬁc product synthesis rate (M  M

1

 T

1

or M  Cel

1

 T

1

Yield coefﬁcients

The yield coefﬁcients that measure the substrate conversion into cells and

substrate conversion into products are also excellent variables for the

characterization of the system, as well as to follow the metabolic changes

of the culture. The substrates are consumed to form cells and products (or

byproducts), and to generate energy. These conversions have characteristic

parallel reactions, as substrate consumption (S) leads to many ‘‘products’’,

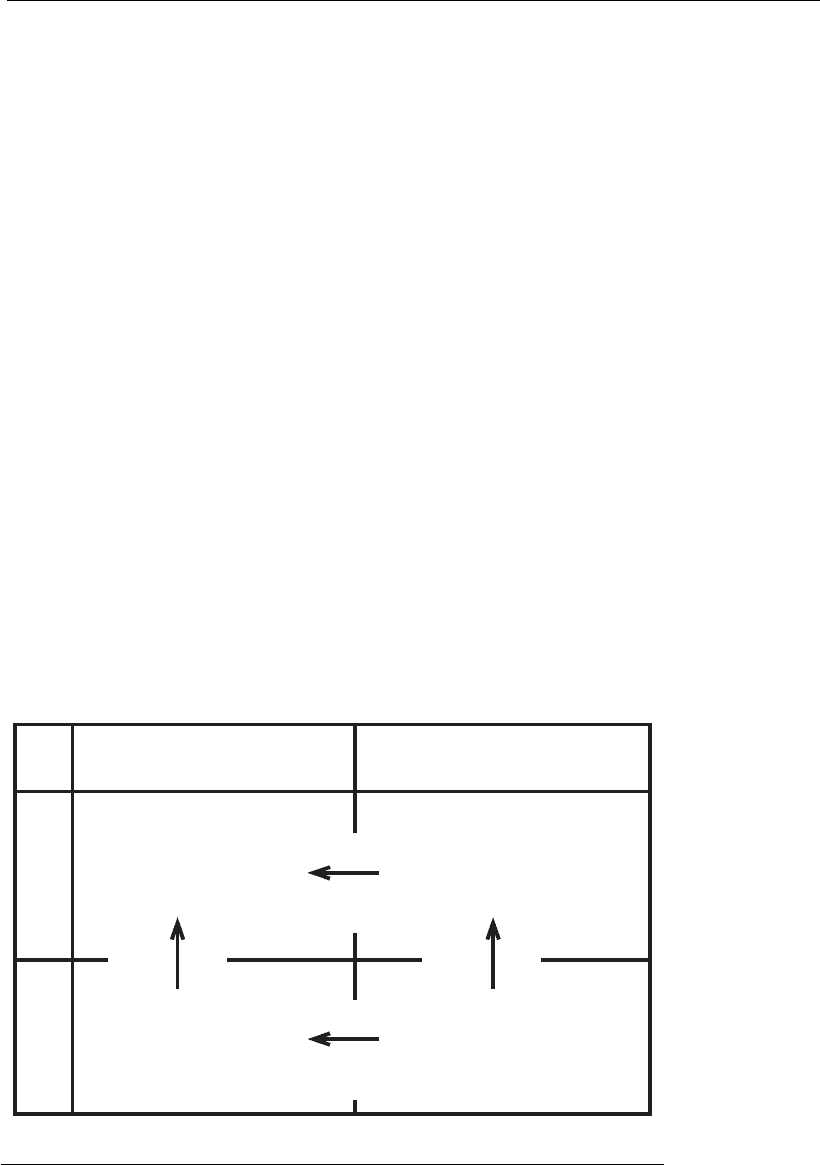
that is, cells, products, and byproducts (Figure 8.3).

The substrate-to-cells or substrate-to-products yield coefﬁcients can be

calculated in an interval of time ˜t, as indicated by Equations 9 and 10.

Substrate (S)

Cells (X)

Product (Pi)

Energy (ATP)

ATP

Figure 8.3

Simpliﬁed schema of the substrate partition between metabolic pathways;

catabolism (used for ATP and ADP synthesis) and anabolism (for biomass

synthesis). The quantities S

indicate the fraction of S destined to formation of the

product ‘‘i’’.

188 Animal Cell Technology

X=S

˜X

˜S

(9)

where:

X=S

¼ substrate-to-cells yield coefﬁcient (or factor)

(M  M

1

or Cel  M

1

);

˜X ¼ cellular concentration variation in the time interval ˜t

(M  L

3

or Cel  L

3

);

˜S

¼ substrate consumption for cell formation in time interval ˜t

(M  L

3

P=S

˜P

˜S

(10)

where:

P=S

¼ substrate-to-product yield coefﬁcient (or factor) (M  M

1

);

˜P ¼ product concentration variation in the time interval ˜t(M L

3

);

˜S

¼ substrate consumption for the product formation in the time

interval ˜t(M L

3

If the ﬁnal destination of the substrate is unique, the yield coefﬁcient (to

cell or products) is a stoichiometric constant that relates reagents to

‘‘products.’’ However, it is frequent that the substrate forms more than

one substance (for example, glucose may be converted to cells and lactate),

or that a speciﬁc product comes from distinct substrates (for example,

lactate formed from glucose and glutamine). In these cases, the calculation

of the real conversion factors is only possible when a labeled reagent is

used, allowing the identiﬁcation of the reagent destination in the metabolic

pathway. In practice, global yield coefﬁcients are often calculated from

total substrate consumption and the total ‘‘products’’ formed, as indicated

in Equations 9 and 10. Instantaneous yields coefﬁcients Y

X=S

and Y

P=S

can

be calculated as a relation between substrate consumption rate and

‘‘products’’ formation rate, as indicated in Equations 11 and 12.

X=S

¼



(11)

P=S

¼



(12)

Finally, oxygen consumption per unit of substrate (Equation 13) is a

factor that helps in understanding the metabolic pathways utilized by the

cells and, therefore, it is useful in system analysis. This not exactly a yield

coefﬁcient, because it establishes a relation of consumption between two

substrates. Similarly, other relations, not exactly yield coefﬁcients (for

example, Y

LAC=X

NH3=X

, etc.), can be calculated and utilized for system

characterization.

¼



(13)

where:

¼ oxygen consumption per unit of substrate factor (M  M

1

);

Mathematical models for growth and product synthesis in animal cell culture 189



¼ speciﬁc oxygen consumption rate

(M  M

1

 T

1

or M  Cel

1

 T

1

8.2.2 Data treatment

The treatment of experimental data is an essential activity to calculate

precise kinetic variables in the equations above. The quality of the kinetic

analysis, the identiﬁcation of relevant phenomena and, subsequently,

model parameter ﬁtting, are directly dependent on the initial data.

This section discusses treatment of experimental data, especially for

conditions where state variables change over time. These are the most

difﬁcult data to treat and correspond to cultures from batch, fed-batch, or

any continuous transient phase. In continuous steady state, the state

variables and rates values do not alter with time, and the rate calculation

results from the algebraic equation solution.

The experimental error is also relevant to data treatment, and will also

be considered in this section. The extent of the analytic error depends on

various factors including the type of methodology adopted, operator

training, and inoculum protocols. The errors are relatively high in bio-

logical systems: for example, 10–30% for proteins concentration; 7–10%

for cells concentration and viability (especially at low viability); 2–5% for

liquid chromatography measures (glucose, lactate, amino acids) (Po

rtner

and Scha

fer, 1996; Miller and Reddy, 1998).

The experimental error of measurements from batch processes is nor-

mally higher than those obtained from a stationary state in processes

conducted in a continuous mode, simply because, in batch, variations in

culture conditions occur during the whole process. In a stationary state of

a continuous process, the kinetic variables are calculated from state

variable average values.

It is always possible to calculate the kinetic variables directly from the

experimental data. However, the values of kinetic variables are of higher

quality when the errors are attenuated and identiﬁed before employing the

treatment data methods.

This attenuation can be made by smoothing methods that allow data

extrapolation, if the number of experimental points is reduced. The

smoothing methods should also allow rate calculation from these points.

The most commonly used smoothing techniques of experimental data are

presented below.

(i) Manual smoothing of the experimental data, which implies tracing

an average curve with experimental points based on previous know-

ledge of the system. Subsequently, the smoothed curve is read,

creating a data table (variable ¼ f(time)).

(ii) Simple mathematical function ﬁtting – linear, logarithmic, or poly-

nomial with low degree regressions. This can be sufﬁcient to obtain

smooth experimental data. By applying the minimal quadratic meth-

od, it is possible to ﬁt any of these functions, minimizing the

difference between real data and those simulated by functions. This is

a relatively easy task, since these functions are available in various

commercial software products. Although it is difﬁcult to represent

190 Animal Cell Technology

the entire culture proﬁle by one curve, it is always possible to ﬁt

different functions to the various phases of culture (iii and iv below).

(iii) Mathematical function ﬁtting by stepwise changes. This approach

aims to represent the growth phase by stepwise changes of functions.

The ‘‘spline’’ method, for example, consists of a series of low degree

polynomial regressions, which ﬁt a low number of experimental

points (3 to 4 points) each time, ensuring continuity between the

various polynomial functions (Lancaster and Salkauskas, 1986).

(iv) A mixed approach combines the smoothing of experimental data,

based on previous knowledge of the system (i), and mathematical

function ﬁtting (linear regression, logarithmic, polynomial, spline,

etc.), as outlined in (ii) and (iii) above.

Once the experimental errors are attenuated, data are prepared for the

calculation of kinetic variables. Frequently, it is necessary to determine the

rates (Equations 4 to 8), and the possible approaches are:

(v) the derivation of mathematical functions ﬁtted, as proposed in (ii) and

(iv) above;

(vi) the calculation of derivatives employing geometrical methods, as Le

Duy and Zajic (1973), applied to experimental smoothed data (Hiss,

2001).

The determination of these rates allows the direct calculation of instan-

taneous yield factors, as in Equations 11 and 12. This form of calculation is

employed whenever these factors change during the cultivation time.

Alternatively, it is possible to determine yield factors by linear regression

of ‘‘product’’ concentration (cell, byproducts, or product) as a function of

the substrate concentration.

8.2.3 Phenomena identiﬁcation

A lot of effort as regards phenomena identiﬁcation is based on speciﬁc

growth rate analysis. In Chapter 2, cell growth and division were proposed

in three phases, based on values of speciﬁc growth rates. The number of

steps observed in a culture depends on each system, that is, some steps

may not exist or have an insigniﬁcant duration under some conditions.

A lag (or latent or adaptation) phase can occur at the beginning of

culture during which no growth occurs, followed by an acceleration phase,

a period in which the speciﬁc growth rate varies until reaching a maximum

value. The analysis of this initial behavior can reveal any problems

connected with preparation of inocula, as well as any substrate inhibition.

The other typical situation is that shown in Figure 8.2E, in which the 

is maximum from the beginning of culture. During the exponential growth

phase, the speciﬁc growth rate remains at the maximum value (

X,max

) until

any nutritional limitation or inhibition by toxic products alters cell

growth. Thus, a speciﬁc growth rate reduction can be observed.

The behavior analysis of the other state variables (substrates and

product concentrations), at the same time as the 

decrease, can indicate

the cause of the metabolism change. For the case exempliﬁed in Figure 8.2

it can be observed that at 47 hours (end of exponential phase) the

Mathematical models for growth and product synthesis in animal cell culture 191