Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_92

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_92.html[22/02/2009 23:52:15]

< previous page page_92 next page >

Page 92

4.7) Let

Find the Fourier series of

and sketch the graph of its limit.

4.8) Find the Fourier series of the function

defined on the interval −1≤

x≤

1 by

and sketch the graph of its limit.

4.9) Show that

Hint: Example 4.5b.

4.10)For each of the following, tell whether or not the Fourier series of the given function converges

uniformly, and explain your answers.

f(x)=ex, −1≤x≤1.

ii)

f(x)=x

2, −1≤

x≤

iii)

f(x)=e−x2, −1≤x≤1.

iv)

f(x)=x

3, −π≤

x≤

π.

4.11)Let f be defined on the interval 0≤

x≤

2 by

i) Find the Fourier cosine series of

and sketch the graph of its limit,

ii) Find the Fourier sine series of

and sketch the graph of its limit.

4.12)Let

be defined by

f(x)=

sin x for 0≤ x

≤π.

i) Find the Fourier sine series of

and sketch the graph of its limit,

ii) Find the Fourier cosine series of

and sketch the graph of its limit.

< previous page page_92 next page >

page_93

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_93.html[22/02/2009 23:52:15]

< previous page page_93 next page >

Page 93

4.13)

Show that the estimate proved in Example 4.20 is sharp for

4.14)

Let

Without any calculations make a rough sketch over −4<

<4 of

i) Fourier sine series of

ii) Fourier cosine series of

iii) Fourier series of

In each case indicate where you would expect a Gibbs phenomenon.

iv) Find a function

g(x)

defined on an interval

such that the Fourier series for g converges uniformly

f(x)

for Are the interval

and the function

uniquely defined?

4.15)Compute the partial sum

of the Fourier sine series for

f(x)=

on [0, 1]. Does

converge as

4.16)

Find the orthogonal projection of

f(x)

= 1 into where solves equation (4.3). Does

PNf

show a Gibbs phenomenon at

0? Does

(PNf)′

show a Gibbs phenomenon at

0? The

eigenvalues will have to be found numerically.

< previous page page_93 next page >

page_94

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_94.html[22/02/2009 23:52:16]

< previous page page_94 next page >

Page 94

This page intentionally left blank.

< previous page page_94 next page >

page_95

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_95.html[22/02/2009 23:52:16]

< previous page page_95 next page >

Page 95

Chapter 5

Eigenfunction Expansions for Equations in Two Independent Variables

Drawing on the Sturm-Liouville eigenvalue theory and the approximation of functions we are now ready

to develop the eigenfunction approach to the approximate solution of boundary value problems for

partial differential equations. All these problems have the same basic structure. We shall outline the

general solution process and then examine the technical differences which arise when it is applied to

the heat, wave and Laplace’s equation. Specific applications and numerical examples are discussed in

subsequent chapters.

We shall consider partial differential equations in two independent variables

(x, t)

where usually

denotes a space coordinate and

stands for time. How ever, on occasion, as in potential problems, both

variables may denote space coordinates. In this case we tend to choose

(x, y)

as independent variables.

All problems to be considered are of the form

(5.1)

where

is a linear partial differential operator, possibly with variable coefficients, defined for

and

Typical examples to be discussed at length in Chapters 6–8 are the heat equation

the wave equation

< previous page page_95 next page >

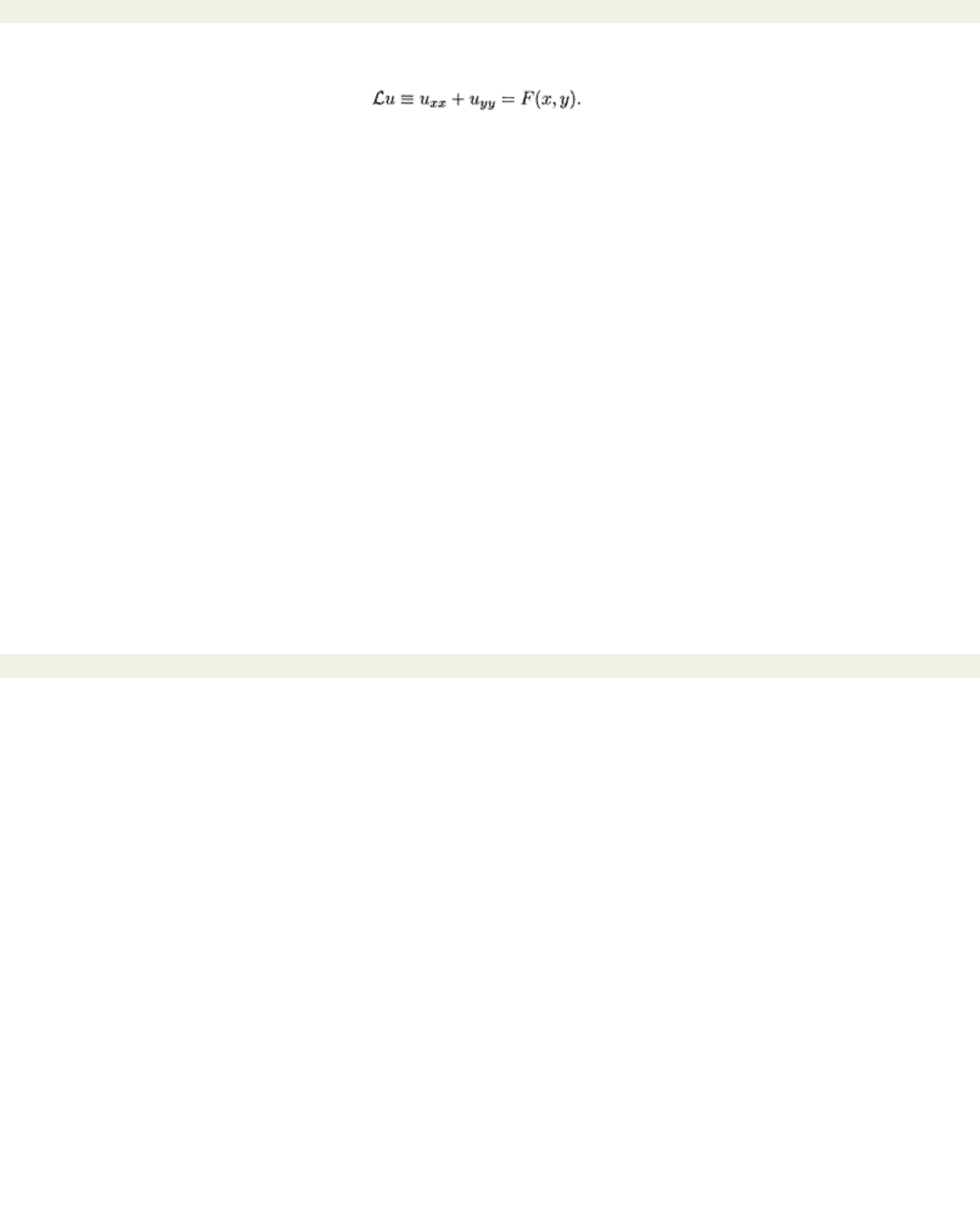
page_96

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_96.html[22/02/2009 23:52:17]

< previous page page_96 next page >

Page 96

and Poisson’s equation (also called the potential equation)

It is characteristic of our eigenfunction expansion view of separation of variables that in all these

equations we admit source terms which are functions of the independent variables.

Equation (5.1) is to be solved for a function

which satisfies linear homogeneous or inhomogeneous

boundary conditions at

0 and

x=L

. Specifically, for our three model problems we expect that

either

satisfies the homogeneous periodicity conditions

(0,

)

=u(L, t)

(0,

)

=ux(L, t)

or the general inhomogeneous boundary conditions

(0,

)−

(0,

)

=A(t)

ux(L, t)+β

u(L, t)=B(t)

for nonnegative parameters

, α

, β

2 and smooth functions

A(t)

and

B(t).

In addition,

is required to satisfy an initial condition at

0 or boundary conditions at

0 and

y=b.

For definiteness, we shall assume that

(

, 0)=

u0(x),

(5.2)

which is typical for the heat equation. Other conditions are discussed when applying the spectral

approach to the wave and potential equation.

For linear inhomogeneous boundary conditions it is possible to find a function

v(x, t)

which satisfies the

boundary conditions imposed on

For example, suppose that the boundary conditions of the problem

are

(0,

)

=A(t)

ux(L, t)=h[B(t)—u(L, t)]

(5.3)

where

and

are given functions of

and

is a positive constant. If we choose a function

v(x, t)

the form

v(x, t)=a(t)+b(t)x,

(5.4)

then it is straightforward to find

and

such that

satisfies (5.3). We need to solve

(0,

)

=α(t)=A(t)

< previous page page_96 next page >

page_97

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_97.html[22/02/2009 23:52:18]

< previous page page_97 next page >

Page 97

vx(L, t)=b(t)=h[B(t)−v(L, t)]=h[B(t)−a(t)−b(t)L]

so that

Note that

v(x, t)

is not unique. We could have chosen, for example

v(x, t)

α(t)

b(t)x

c(t)x

and determined

α(t), b(t),

and

c(t)

so that this

satisfies the given boundary conditions. In this case

there will be infinitely many solutions. In general, the form of (5.4) for

is the simplest choice and leads

to the least amount of computation, provided

and

can be found. If not, a quadratic in

will succeed

(see Example 8.2). On special occasions a

structured to the problem must be used (see Example 6.8).

If we now set

w(x, t)

u(x, t)−v(x, t),

then

will satisfy one of the boundary conditions listed in Table 3.1. For equation (5.3) we would

obtain

(0,

)=0

wx(L, t)=−hw(L, t).

In other words, the function

w(x, t)

as a function of

belongs to one of the subspaces

discussed in

Chapter 3, and this subspace does not change with

Excluded from our discussion are nonlinear boundary conditions like the so-called radiation condition

ux(L, t)=h[B

(t)−u

(L, t)]

or a reflection condition like

ux(L, t)=−h(t)u(L, t)

for a time-dependent function

Transforming the problem for

with inhomogeneous boundary conditions into an equivalent problem for

with homogeneous boundary conditions is the first step in applying any form of separation of

variables. Once this is done the problem can be restated for

as:

< previous page page_97 next page >

page_98

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_98.html[22/02/2009 23:52:18]

< previous page page_98 next page >

Page 98

Find a function

w(x, t)

which satisfies

(5.5)

which satisfies the corresponding homogeneous boundary conditions at

0 and

and which

satisfies the given conditions at

0 (and, if applicable, at

y=b

), i.e., here

(5.6)

We emphasize that

and

0 are known data functions.

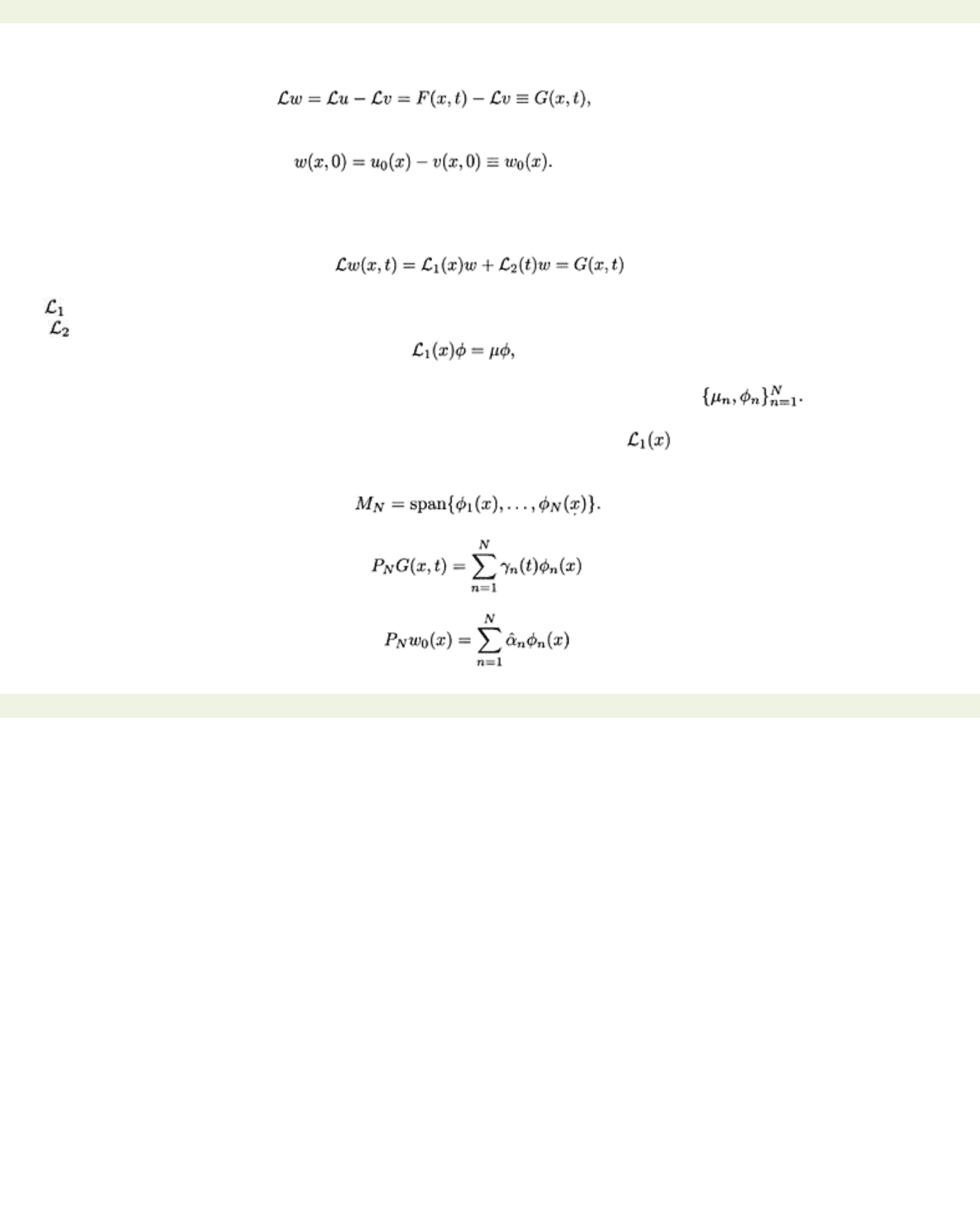
We now make the following two essential assumptions which lie at the heart of any separation of

variables method:

I) The partial differential equation (5.5) can be written in the form

where

denotes the terms involving functions of x and derivatives with respect to

ii) denotes the terms involving functions of t and derivatives with respect to

II) The eigenvalue problem

subject to one of the boundary conditions of (3.2), has obtainable solutions

In all of our

applications the eigenvalue problem is a SturmLiouville eigenvalue problem so that the eigenfunctions

are orthogonal in an inner product space M which is determined by

and the boundary conditions.

The computation of an approximate solution of (5.5), (5.6) is now automatic.

We define

We compute the best approximations, i.e., the projections

< previous page page_98 next page >

page_99

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_99.html[22/02/2009 23:52:19]

< previous page page_99 next page >

Page 99

of the space-dependent data functions (treating

as a parameter) and solve the approximating problem

(5.7)

We compute an exact solution

w(x, t)

of (5.7) by assuming that it belongs to

for all

In this case it

has to have the form

We want and

and so the coefficients

{αn(t)}

must be chosen such that

Since the eigenfunctions

are linearly independent, the term in the bracket must vanish. Hence

each coefficient

αn(t)

has to satisfy the ordinary differential equation

and the initial condition

The techniques of ordinary differential equations give us explicit solutions

{αn(t)}.

It may generally be

assumed that the problem (5.7) for

is well posed so that the

just constructed is the only solution

of (5.7).

So far the specific form of

has not entered our discussion. Hence, regardless of whether we solve

the heat equation, the wave equation, or Laplace’s equation, the solution process always consists of the

following steps:

Step 1: Find a function

which satisfies the same boundary conditions at

=0 and

x=L

as the unknown

solution

u(x, t)

Step 2: Set

w=u−v

and write problem (5.5)

the linear homogeneous boundary conditions at

0 and

x=L,

and the conditions for

0 (or at

0 and

y=b

Step 3: For these boundary conditions solve the eigenvalue problem

< previous page page_99 next page >

page_100

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_100.html[22/02/2009 23:52:20]

< previous page page_100 next page >

Page 100

for the first N eigenvalues and eigenvectors.

Step 4: Project

G(x, t)

and the initial or boundary conditions at

=0 (or at

=0 and

) into the span

of these

eigenfunctions, treating

as a parameter, to obtain the approximating problem (5.7).

Step 5: for

wN.

Step 6: Accept as an approximation to the solution

of the original problem the computed solution

uN=wN

To illustrate the problem independence of these steps, but also to highlight some of the computational

differences in carrying them out for varying initial and boundary conditions we shall discuss in a

qualitative sense the solution process for the heat, the wave, and the potential equation.

The eigenfunction method, also known as spectral method, is easiest to apply to the heat equation.

Thus let us consider the initial/boundary value problem

It models the temperature distribution

u(x, t)

in a slab of thickness

(or an insulated bar of length

) as

a function of position and a scaled time.

F(x, t)

denotes an internal heat source or sink, and

A(t)

and

B(t)

are a prescribed (and generally time-dependent) temperature and flux at the ends of the slab or

bar. The initial temperature distribution is

(x).

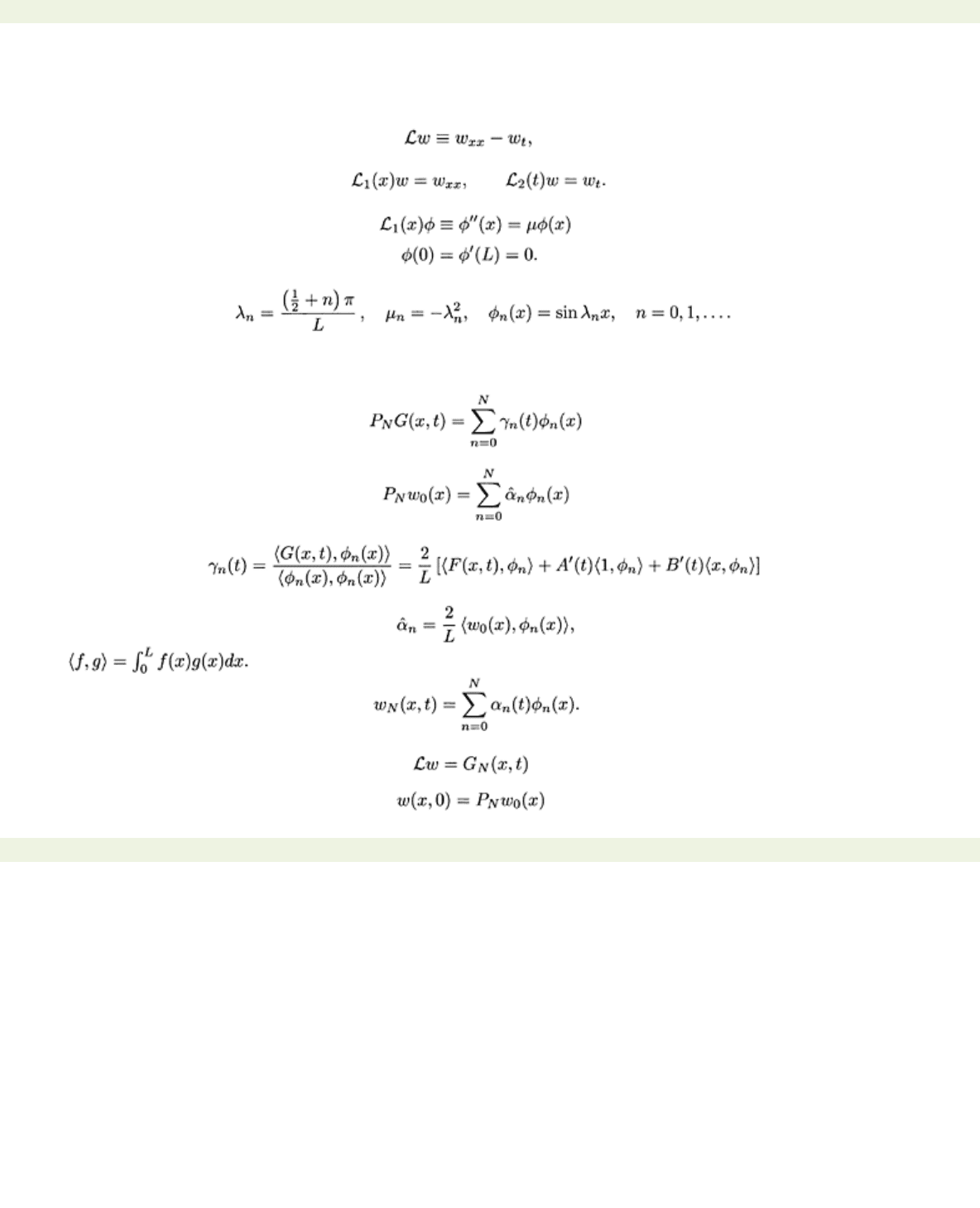
In order to rewrite the problem for homogeneous boundary conditions we choose

v(x, t)=A(t)+B(t)x,

which satisfies the boundary conditions imposed on

u(x, t),

and define

w(x, t)=u(x, t)

−

v(x, t).

Then

< previous page page_100 next page >

page_101

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_101.html[22/02/2009 23:52:21]

< previous page page_101 next page >

Page 101

Here we have assumed that

and

are differentiable. We shall see below that the final result depends

only on

and

not their derivatives.

Since

we see that

The homogeneous boundary conditions at

0 and

x=L

dictate that we solve the eigenvalue problem

The eigenvalues and eigenfunctions are available from Table 3.1 as

Because the eigenfunctions are orthogonal in

2(0,

), we readily can approximate the source term

and the initial condition

in the span

of the first

+1 eigenfunctions.

and

PNw

0 are the

orthogonal projections

where

with

The solution of the approximating problem can be expressed as

Substitution into

< previous page page_101 next page >