Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach
Подождите немного. Документ загружается.


page_112
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_112.html[22/02/2009 23:52:29]
< previous page page_112 next page >
Page 112
can be solved in terms of
C(t)
without ever computing
C″(t).
5.17)Apply the solution process of this chapter to find an approximate solution of the vibrating beam
problem
(see Exercise 3.14).
5.18)Apply the solution process of this chapter to find an approximate solution of the problem
this problem twice: once with eigenfunctions of the independent variable
x,
the second time with
eigenfunctions of the independent variable
y.
5.19)Apply the solution process of this chapter to find an approximate solution of the problem
5.20)Determine
F(x, y)
and
g(x, y)
such that
u(x, y)=(x+y)
2
is a solution of
Now solve this Dirichlet problem in the following two ways:
< previous page page_112 next page >

page_113
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_113.html[22/02/2009 23:52:30]
< previous page page_113 next page >
Page 113
i) Use the solution process of this chapter to find an approximate solution
uN(x, y)
in terms of
eigenfunctions which are functions of
x.
Compute
e(x, y)=PNu(x, y)−uN(x, y).
ii) Use the solution process of this chapter to find an approximate solution
uN(x, y)
in terms of
eigenfunctions which are functions of
y.
Compute
e(x, y)
=
PNu(x, y)−uN(x, y).
5.21)Determine
F(x, y)
and
g(x, y)
such that
u(x, y)=(xy)2
is a solution of
Now solve this Neumann problem in the following two ways:
i) Use the solution process of this chapter to find an approximate solution
uN(x, y)
in terms of
eigenfunctions which are functions of
x.
Compute
e(x, y)=PNu(x, y)−uN(x, y).
ii) Use the solution process of this chapter to find an approximate solution
uN(x, y)
in terms of
eigenfunctions which are functions of
y.
Compute
e(x, y)=PNu(x, y)−uN(x, y).
< previous page page_113 next page >

page_114
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_114.html[22/02/2009 23:52:30]
< previous page page_114 next page >
Page 114
This page intentionally left blank.
< previous page page_114 next page >

page_115
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_115.html[22/02/2009 23:52:31]
< previous page page_115 next page >
Page 115
Chapter 6
One-Dimensional Diffusion Equation
The general solution process of the last chapter will be applied to diffusion problems of increasing
complexity. Our aim is to demonstrate that separation of variables, in general, and the eigenfunction
expansion method, in particular, can provide quantitative and numerical answers for a variety of realistic
problems. These problems are usually drawn from conductive heat transfer, but they have natural
analogues in other diffusion contexts, such as mass transfer, flow in a porous medium, and even option
pricing. The chapter concludes with some theoretical results on the convergence of the approximate
solution to the exact solution and on the relationship between the eigenfunction expansion and
Duhamel’s superposition method for problems with time-dependent source terms.
6.1 Applications of the eigenfunction expansion method
Example 6.1 How many terms of the series solution are enough?
At the end of this chapter we shall discuss some theoretical error bounds for the approximate solution of
the heat equation. However, for some problems very specific information is available which can provide
insight into the solution process and the quality of the answer. To illustrate this point we shall consider
the model problem
< previous page page_115 next page >

page_116
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_116.html[22/02/2009 23:52:31]
< previous page page_116 next page >
Page 116
This is a common problem in every text on separation of variables. It describes a thermal system initially
in a uniform state which is shocked at time
t=
0 with an instantaneous temperature rise. The parameter
α
in the above heat equation is the so-called diffusivity of the medium and is included (rather than set
to 1 by rescaling time) to show explicitly the dependence of
u
on
α.
It is known from the theory of partial differential equations that this problem has a unique infinitely
differentiate solution
u(x, t)
on (0,
L
)×(0,
T
] for all
T
>0, and which takes on the boundary and initial
conditions. However, since
the solution is discontinuous at (0, 0). As we shall see this discontinuity will introduce a Gibbs
phenomenon into our approximating problem. We shall com-pute an approximate solution
uN(x, t)
and
would like to get an idea of how large
N
should be in order to obtain a good solution.
The problem is transformed to one with zero boundary data by subtracting the steady-state solution
We set
w(x, t)=u(x, t)−v(x).
Then
The associated eigenvalue problem is
The eigenfunctions are with and The approximating problem in the
span of the first
N
eigenfunctions is readily found. In this case the source term
G
is zero so that
< previous page page_116 next page >

page_117
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_117.html[22/02/2009 23:52:32]
< previous page page_117 next page >
Page 117
i.e.
γ
n
(t)
=0 for all
n
.
The projection of the initial condition is
with
Since the odd extension of
−v(x)
to
[−L, L]
has a jump at
x=
0, we expect a Gibbs phenomenon in the
approximation of
v(x)
in terms of the
The solution of
is given by
where
It follows from (5.8) that the exact solution of the approximating problem is
(6.1)
The time-dependent terms in (6.1) constitute the so-called transient part of the solution. The infinite
series obtained from (6.1) as is generally considered the separation of variables solution of the
problem, but only the finite sum in (6.1) can be computed. In practice
uN(x, t)
is evaluated for a given
x
and
t
and a few
N.
If changes in the answer with
N
become insignificant, the last computed value is
accepted as the solution of the original problem. However, for small
t
this N can be quite large as the
following argument shows.
We know from our discussion of the Gibbs phenomenon that
uN
(
x,
0) converges to
u
0
(x)
only pointwise
on (0,
L
] as and that
< previous page page_117 next page >

page_118
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_118.html[22/02/2009 23:52:33]
< previous page page_118 next page >
Page 118
We shall now show that for
t>
0 the approximate solution
uN(x, t)
converges uniformly on [0,
L
] as Let
N>M,
then
where
We see that
R
→0 as
M
→∞ for all
N>M
independently of If is accepted as the
analytic solution of the original problem, then
R
(
αt, M
+1) is a bound on the error. We can estimate
M
such that for any given For example, suppose we wish to assure that our solution at time
αt
=.00001 is within 10−6 of the analytic solution. With
L
=1 we find that
R
(10−5, 334) <10−6 <
R
(10−5, 333).
Hence 333 terms in the transient solution are sufficient for the approximate solution. Of course, our
estimates are not sharp, but we are not far off the mark. For example, a numerical evaluation of (6.1)
for
N=
300 and
αt=
10−5 yields
Since the analytic solution is nonnegative, the error exceeds our tolerance. (We remark that for
N
=333
min
u
333
(x, t)
= −0.83×10−6
is within our tolerance.)
For illustration we show in Fig. 6.1
u
10
(x, t)
and
u
333
(x, t)
for
αt=
10−5 to caution that one cannot
always truncate the series after just a few terms.
In contrast, similar estimates for
αt=
.1 show that only three terms are required in the transient solution
for an error less than 10−6.
< previous page page_118 next page >
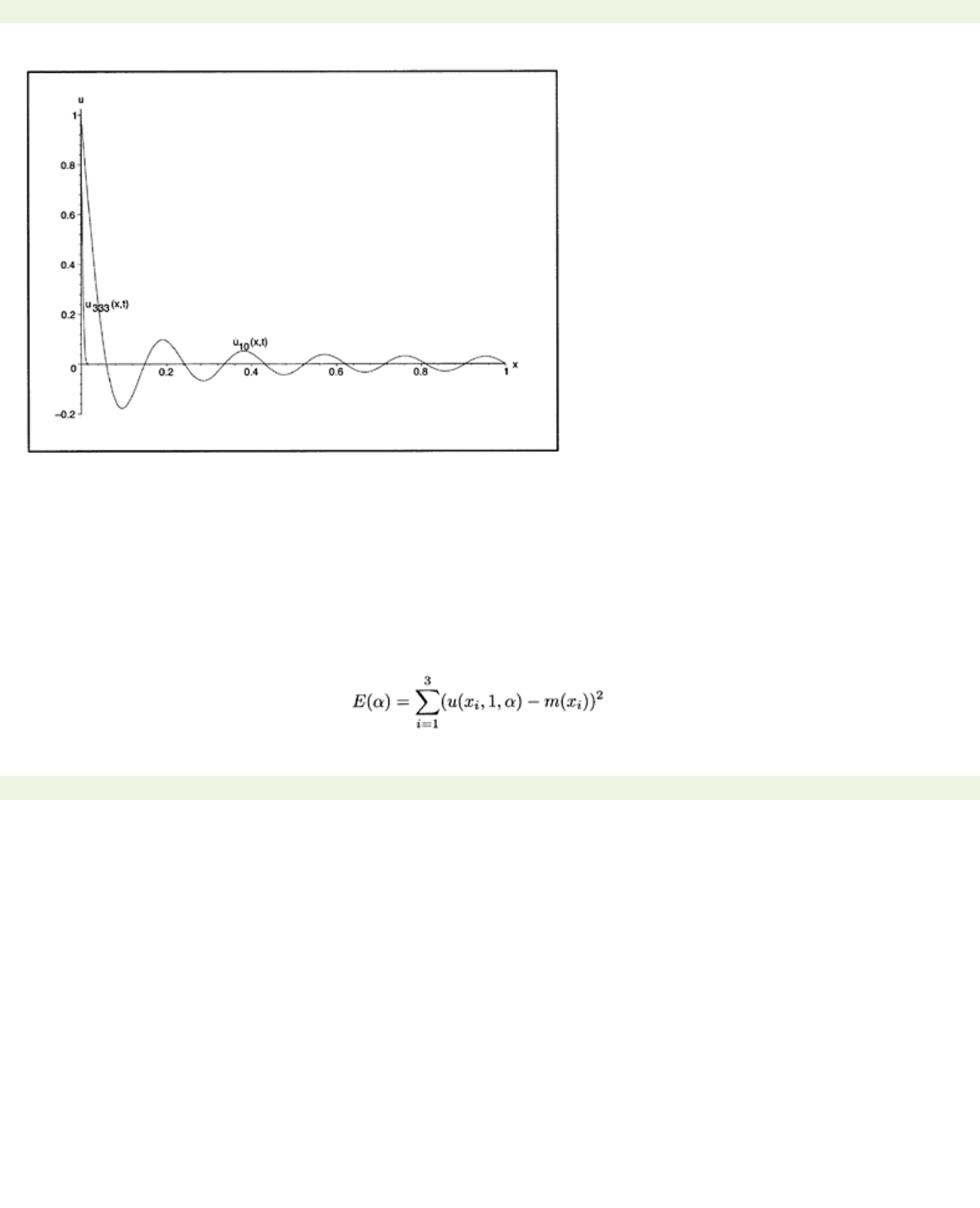
page_119
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_119.html[22/02/2009 23:52:34]
< previous page page_119 next page >
Page 119
Figure 6.1:1Plot of
uN(x, t)
for
N=
10 and
N=
333 at
at=
10−5.
Example 6.2 Determination of an unknown diffusivity from measured data.
The advantage of an analytic solution is particularly pronounced when it comes to an estimation of
parameters in the equation from observed data. We shall illustrate this point with the model problem of
Example 6.1, but this time we shall assume that the diffusivity of the medium is not known. Instead at
time
t=
1 we have temperature measurements
m
(1/4)=.4
m
(1/2)=.1
m
(3/4)=.01
recorded at
x=
1/4,
x=
1/2, and
x=
3/4. We want to find a constant diffusivity
α
for which (6.1) best
matches the measurements in the least squares sense, i.e., we need to minimize
1 Subsequently, figures and tables are numbered according to the examples in which they appear.
< previous page page_119 next page >

page_120
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_120.html[22/02/2009 23:52:34]
< previous page page_120 next page >
Page 120
where
xi
=i/4,
i
=1, 2, 3. Considering the crudeness of the model we shall be content to graph
E(α)
vs.
y=eα
and read off where it has a minimum. Fig. 6.2 shows
E(α)
when
N=
5. There appears to be a
unique minimum.
Figure 6.2: Plot of
E(α)
vs.
eα.
The diffusivity minimizing the error is observed to be
α=
.0448.
The temperatures predicted by this
α
are
u
(1/4, 1)=.403,
u
(1/2,1)=.095,
u
(3/4,1)=.0122.
t=
1 is large enough that increasing the number of terms in our approximate solution does not change
the answer. In fact,
N
=5 is consistent with an error of less than 10−6 as discussed in Example 6.1.
Example 6.3 Thermal waves.
Our next example introduces flux data at
x=L
.
We consider
< previous page page_120 next page >

page_121
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_121.html[22/02/2009 23:52:35]
< previous page page_121 next page >
Page 121
This is a standard companion problem to that of Example 6.1. It describes heat flow in a slab or axial
flow in a bar where the right end of the slab or bar is perfectly insulated. Its solution is straightforward.
The boundary data are zeroed out by choosing
v(x)=
1
(again the steady-state solution of the problem) and setting
w(x, t)=u(x, t)−v(x).
Then
The associated eigenvalue problem is
which has the solutions
The approximating problem is
where
We expect a Gibbs phenomenon in the approximation to
w
(
x,
0) at
x=
0. The approximate solution to
our problem is
(6.2)
The simple formula (6.2) has a surprising consequence. The solution
uN(x, t)
at
x=L
is seen to be a
linear combination of the functions
< previous page page_121 next page >
