Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach
Подождите немного. Документ загружается.


page_viii
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_viii.html[22/02/2009 23:50:52]
< previous page page_viii next page >
Page viii
suitably chosen, then
uN
is a good approximation to the unknown solution
u
. As we shall see,
M
will be
defined such that
uN
is just the partial sum of the first
N
terms of the infinite series traditionally
associated with the method of separation of variables.
The reader may recognize this view as identical to the setting of the finite element, collocation, and
spectral methods that have been developed for the numerical solution of differential equations. All these
methods differ in how the subspace
M
is chosen and in what sense the original problem is
approximated. These choices dictate how hard it is to compute the approximate solution
uN
and how
well it approximates the analytic solution
u
.
Given the almost universal applicability of numerical methods for the solution of partial differential
equations, the question arises whether separation of variables with its severe restrictions on the type of
equation and the geometry of the problem is still a viable tool and deserves further exposition. The
existence of this text reflects our view that the method of separation of variables still belongs to the
core of applied mathematics. There are a number of reasons.
Closed form (approximate) solutions show structure and exhibit explicitly the influence of the problem
parameters on the solution. We think, for example, of the decomposition of wave motion into standing
waves, of the relationship between driving frequency and resonance in sound waves, of the influence of
diffusivity on the rate of decay of temperature in a heated bar, or of the generation of equipotential and
stream lines for potential flow. Such structure and insight are not readily obtained from purely numerical
solutions of the underlying differential equation. Moreover, optimization, control, and inverse problems
tend to be easier to solve when an analytic representation of the (approximate) solution is available. In
addition, the method is not as limited in its applicability as one might infer from more elementary texts
on separation of variables. Approximate solutions are readily computable for problems with time-
dependent data, for diffusion with convection and wave motion with dissipation, problems seldom seen
in introductory textbooks. Even domain restrictions can sometimes be overcome with embedding and
domain decomposition techniques. Finally, there is the class of singularly perturbed and of higher
dimensional problems where numerical methods are not easily applied while separation of variables still
yields an analytic approximate solution.
Our rationale for offering a new exposition of separation of variables is then twofold. First, although
quite common in more advanced treatments (such as [15]), interpreting the separation of variables
solution as an eigenfunction expansion is a point of view rarely taken when introducing the method to
students. Usually the formalism is based on a product solution for the partial differential equation, and
this limits the applicability of the method to homogeneous partial differential equations. When source
terms do appear, then a reformulation of problems for the heat and wave equation with the help of
Duhamel’s superposition principle and an approximation of the source term in the potential equation
with the help of an eigenfunction approximation become necessary. In an exposition based from the
beginning on an eigenfunction expansion, the presence of source terms in the differential equation is
only a technical, but not a conceptual
< previous page page_viii next page >

page_ix
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_ix.html[22/02/2009 23:50:53]
< previous page page_ix next page >
Page ix
complication, regardless of the type of equation under consideration. A concise algorithmic approach
results.
Equally important to us is the second reason for a new exposition of the method of separation of
variables. We wish to emphasize the power of the method by solving a great variety of problems which
often go well beyond the usual textbook examples. Many of the applications ask questions which are not
as easily resolved with numerical methods as with analytic approximate solutions. Of course, evaluation
of these approximate solutions usually relies on numerical methods to integrate, solve linear systems or
nonlinear equations, and to find values of special functions, but these methods by now may be
considered universally available “black boxes.” We are, however, mindful of the gap between the
concept of a solution in principle and a demonstrably computable solution and try to convey our
experience with how well the eigenfunction approach actually solves the sample problems.
The method of separation of variables from a spectral expansion view is presented in nine chapters.
Chapter 1 collects some background information on the three dominant equations of this text, the
potential equation, the heat equation, and the wave equation. We refer to these results when applying
and analyzing the method of separation of variables.
Chapter 2 contains a discussion of orthogonal projections which are used time and again to approximate
given data functions in a specified finite-dimensional but parameter-dependent subspace.
Chapter 3 introduces the subspace whose basis consists of the eigenfunctions of a so-called Sturm-
Liouville problem associated with the application under consideration. These are the eigenfunctions of
the title of this text. We cite results from the Sturm-Liouville theory and provide a table of eigenvalues
and eigenfunctions that arise in the method of separation of variables.
Chapter 4 treats the case in which the eigenfunctions are sine and cosine functions with a common
period. In this case the projection into the subspace is closely related to the Fourier series
representation of the data functions. Precise information about the convergence of the Fourier series is
known. We cite those results which are helpful later on for the application of separation of variables.
Chapter 5 constitutes the heart of the text. We consider a partial differential equation in two
independent variables with a source term and subject to boundary and initial conditions. We give the
algorithm for approximating such a problem and for solving it in a finite-dimensional space spanned by
eigenfunctions determined by the “spacial part” of the equation and its boundary conditions. We
illustrate in broad outline the application of this approach to the heat, wave, and potential equations.
Chapter 6 gives an expansive exposition of the algorithm for the one-dimensional heat equation. It
contains many worked examples with comments on the numerical performance of the method, and
concludes with a rudimentary analysis of the error in the approximate solution.
Chapter 7 parallels the previous chapter but treats the wave equation.
< previous page page_ix next page >

page_x
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_x.html[22/02/2009 23:50:53]
< previous page page_x next page >
Page x
Chapter 8 deals with the potential equation. It describes how one can precondition the data of problems
with smooth solutions in order not to introduce artificial discontinuities into the separation of variables
solution. We solve potential problems with various boundary conditions and conclude with a calculation
of eigenfunctions for the two-dimensional Laplacian.
Chapter 9 uses the eigenfunctions of the preceding chapter to find eigenfunction expansion solutions of
two- and three-dimensional heat, wave, and potential equations.
This text is written for advanced undergraduate and graduate students in science and engineering with
previous exposure to a course in engineering mathematics, but not necessarily separation of variables.
Basic prerequisites beyond calculus are familiarity with linear algebra, the concept of vector spaces of
functions, norms and inner products, the ability to solve linear inhomogeneous first and second order
ordinary differential equations, and some contact with practical applications of partial differential
equations.
The book contains more material than can (and should) be taught in a course on separation of
variables. We have introduced the eigenfunction approach to our own students based on an early
version of this text. We covered parts of Chapters 2–4 to lay the groundwork for an extensive discussion
of Chapter 5. The remainder of the term was filled by working through selected examples involving the
heat, wave, and potential equation. We believe that by term’s end the students had an appreciation that
they could solve realistic problems. Since we view Chapters 2–5 as suitable for teaching separation of
variables, we have included exercises to help deepen the reader’s understanding of the eigenfunction
approach. The examples of Chapters 6–8 and their exercise sets generally lend themselves for project
assignments.
This text will put a bigger burden on the instructor to choose topics and guide students than more
elementary texts on separation of variables that start with product solutions. The instructor who
subscribes to the view put forth in Chapter 5 should find this text workable. The more advanced
applications, such as interface, inverse, and multidimensional problems, as well as the the more
theoretical topics require more mathematical sophistication and may be skipped without breaking
continuity.
The book is also meant to serve as a reference text for the method of separation of variables. We hope
the many examples will guide the reader in deciding whether and how to apply the method to any given
problem. The examples should help in interpreting computed solutions, and should give insight into
those cases in which formal answers are useless because of lack of convergence or unacceptable
oscillations. Chapters 1 and 9 are included to support the reference function. They do not include
exercises.
We hasten to add that this text is not a complete reference book. We do not attempt to characterize the
equations and coordinate systems where a separation of variables is applicable. We do not even mention
the various coordinate systems (beyond cartesian, polar, cylindrical, and spherical) in which the
Laplacian is separable. We have not scoured the literature for new and innovative applications of
separation of variables. Moreover, the examples we do
< previous page page_x next page >

page_xi
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xi.html[22/02/2009 23:50:54]
< previous page page_xi next page >
Page xi
include are often meant to show structure rather than represent reality because in general little
attention is given to the proper scaling of the equations.
There does not appear to exist any other source that could serve as a practical reference book for the
practicing engineer or scientist. We hope this book will alert the reader that separation of variables has
more to offer than may be apparent from elementary texts.
Finally, this text does not mention the implementation of our formulas and calculations on the computer,
or do we provide numerical algorithms or programs. Yet the text, and in particular our numerical
examples, could not have been presented without access to symbolic and numerical packages such as
Maple, Mathematica, and Matlab. We consider our calculations and the graphical representation of their
results routine and well within the competence of today’s students and practitioners of science and
engineering.
< previous page page_xi next page >

page_xii
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xii.html[22/02/2009 23:50:54]
< previous page page_xii next page >
Page xii
This page intentionally left blank.
< previous page page_xii next page >

page_xiii
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xiii.html[22/02/2009 23:50:55]
< previous page page_xiii next page >
Page xiii
Contents
Acknowledgments v
Preface vii
1 Potential, Heat, and Wave Equation 1
1.1 Overview 1
1.2 Classification of second order equations 2
1.3 Laplace’s and Poisson’s equation 3
1.4 The heat equation 11
1.5 The wave equation 18
2 Basic Approximation Theory 25
2.1 Norms and inner products 26
2.2 Projection and best approximation 29
2.3 Important function spaces 34
3 Sturm—Liouville Problems 45
3.1 Sturm-Liouville problems for
45
3.2 Sturm-Liouville problems for
53
3.3 A Sturm-Liouville problem with an interface 59
4 Fourier Series 67
4.1 Introduction 67
4.2 Convergence 68
4.3 Convergence of Fourier series 74
4.4 Cosine and sine series 77
4.5 Operations on Fourier series 80
4.6 Partial sums of the Fourier series and the Gibbs phenomenon 84
5 Eigenfunction Expansions for Equations in Two Independent Variables 95
< previous page page_xiii next page >
page_xiv
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xiv.html[22/02/2009 23:50:55]
< previous page page_xiv next page >
Page xiv
6 One-Dimensional Diffusion Equation 115
6.1 Applications of the eigenfunction expansion method 115
Example 6.1 How many terms of the series solution are enough? 115
Example 6.2 Determination of an unknown diffusivity from measured data 119
Example 6.3 Thermal waves 120
Example 6.4 Matching a temperature history 125
Example 6.5 Phase shift for a thermal wave 129
Example 6.6 Dynamic determination of a convective heat transfer coefficient from measured
data
131
Example 6.7 Radial heat flow in a sphere 134
Example 6.8 A boundary layer problem 137
Example 6.9 The Black-Scholes equation 139
Example 6.10 Radial heat flow in a disk 142
Example 6.11 Heat flow in a composite slab 146
Example 6.12 Reaction-diffusion with blowup 148
6.2 Convergence of
uN(x, t)
to the analytic solution 151
6.3 Influence of the boundary conditions and Duhamel’s solution 155
7 One-Dimensional Wave Equation 161
7.1 Applications of the eigenfunction expansion method 161
Example 7.1 A vibrating string with initial displacement 161
Example 7.2 A vibrating string with initial velocity 166
Example 7.3 A forced wave and resonance 168
Example 7.4 Wave propagation in a resistive medium 171
Example 7.5 Oscillations of a hanging chain 175
Example 7.6 Symmetric pressure wave in a sphere 177
Example 7.7 Controlling the shape of a wave 180
Example 7.8 The natural frequencies of a uniform beam 182
Example 7.9 A system of wave equations 185
7.2 Convergence of
uN(x, t)
to the analytic solution 188
7.3 Eigenfunction expansions and Duhamel’s principle 190
8 Potential Problems in the Plane 195
8.1 Applications of the eigenfunction expansion method 195
Example 8.1 The Dirichlet problem for the Laplacian on a rectangle 195
Example 8.2 Preconditioning for general boundary data 201
Example 8.3 Poisson’s equation with Neumann boundary data 213
Example 8.4 A discontinuous potential 215
Example 8.5 Lubrication of a plane slider bearing 218
Example 8.6 Lubrication of a step bearing 220
Example 8.7 The Dirichlet problem on an
L
-shaped domain 221
Example 8.8 Poisson’s equation in polar coordinates 225
Example 8.9 Steady-state heat flow around an insulated pipe I 230
Example 8.10 Steady-state heat flow around an insulated pipe II 232
< previous page page_xiv next page >

page_xv
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xv.html[22/02/2009 23:50:56]
< previous page page_xv next page >
Page xv
Example 8.11 Poisson’s equation on a triangle 234
8.2 Eigenvalue problem for the two-dimensional Laplacian 237
Example 8.12 The eigenvalue problem for the Laplacian on a rectangle 237
Example 8.13 The Green’s function for the Laplacian on a square 239
Example 8.14 The eigenvalue problem for the Laplacian on a disk 243
Example 8.15 The eigenvalue problem for the Laplacian on the surface of a sphere 244
8.3 Convergence of
uN(x, y)
to the analytic solution 247
9 Multidimensional Problems 255
9.1 Applications of the eigenfunction expansion method 255
Example 9.1 A diffusive pulse test 255
Example 9.2 Standing waves on a circular membrane 258
Example 9.3 The potential inside a charged sphere 260
Example 9.4 Pressure in a porous slider bearing 261
9.2 The eigenvalue problem for the Laplacian in
265
Example 9.5 An eigenvalue problem for quadrilaterals 265
Example 9.6 An eigenvalue problem for the Laplacian in a cylinder 266
Example 9.7 Periodic heat flow in a cylinder 267
Example 9.8 An eigenvalue problem for the Laplacian in a sphere 269
Example 9.9 The eigenvalue problem for Schrödinger’s equation with a spherically symmetric
potential well
271
Bibliography 277
Index 279
< previous page page_xv next page >

page_xvi
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_xvi.html[22/02/2009 23:50:56]
< previous page page_xvi next page >
Page xvi
This page intentionally left blank.
< previous page page_xvi next page >
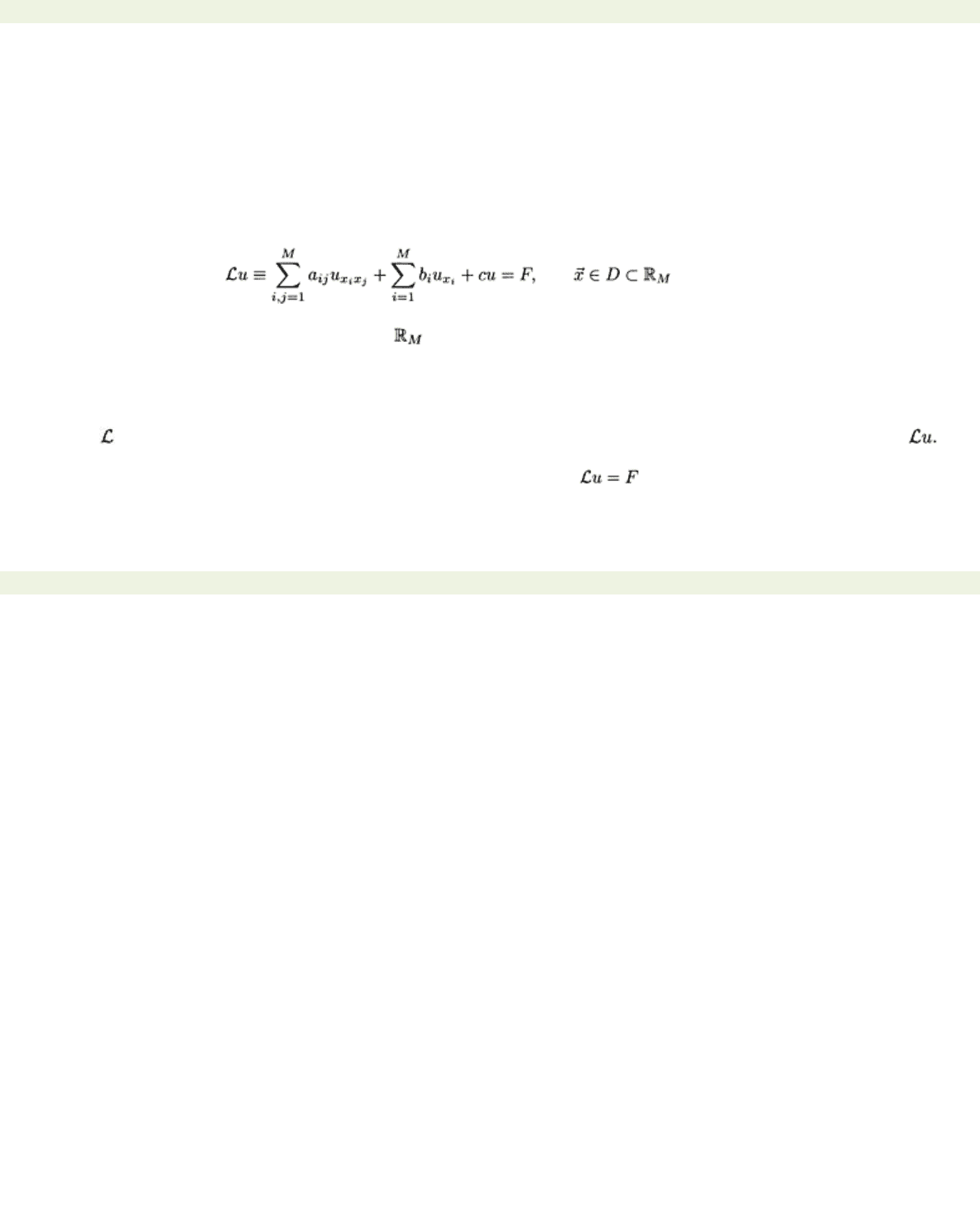
page_1
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_1.html[22/02/2009 23:50:57]
< previous page page_1 next page >
Page 1
Chapter 1
Potential, Heat, and Wave Equation
This chapter provides a quick look into the vast field of partial differential equations. The main goal is to
extract some qualitative results on the three dominant equations of mathematical physics, the potential,
heat, and wave equation on which our attention will be focused throughout this text.
1.1 Overview
When processes that change smoothly with two or more independent variables are modeled
mathematically, then partial differential equations arise. Most common are second order equations of
the general form
(1.1)
where the coefficients and the source term may depend on the independent variables
{x
1,…,
xM},
on
u,
and on its derivatives.
D
is a given set in (whose boundary will be denoted by
∂D
). The equation
may reflect conservation and balance laws, empirical relationships, or may be purely phenomenological.
Its solution is used to explain, predict, and control processes in a bewildering array of applications
ranging from heat, mass, and fluid flow, migration of biological species, electrostatics, and molecular
vibration to mortgage banking.
In (1.1) is known as a partial differential operator that maps a smooth function u to the function
Throughout this text a smooth function denotes a function with as many continuous derivatives as are
necessary to carry out the operations to which it is subjected. is the equation to be solved.
Given a partial differential equation and side constraints on its solution, typically initial and boundary
conditions, it becomes a question of mathematical analysis to establish whether the problem has a
solution, whether the solution
< previous page page_1 next page >
