Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_42

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_42.html[22/02/2009 23:51:35]

< previous page page_42 next page >

Page 42

2.23)

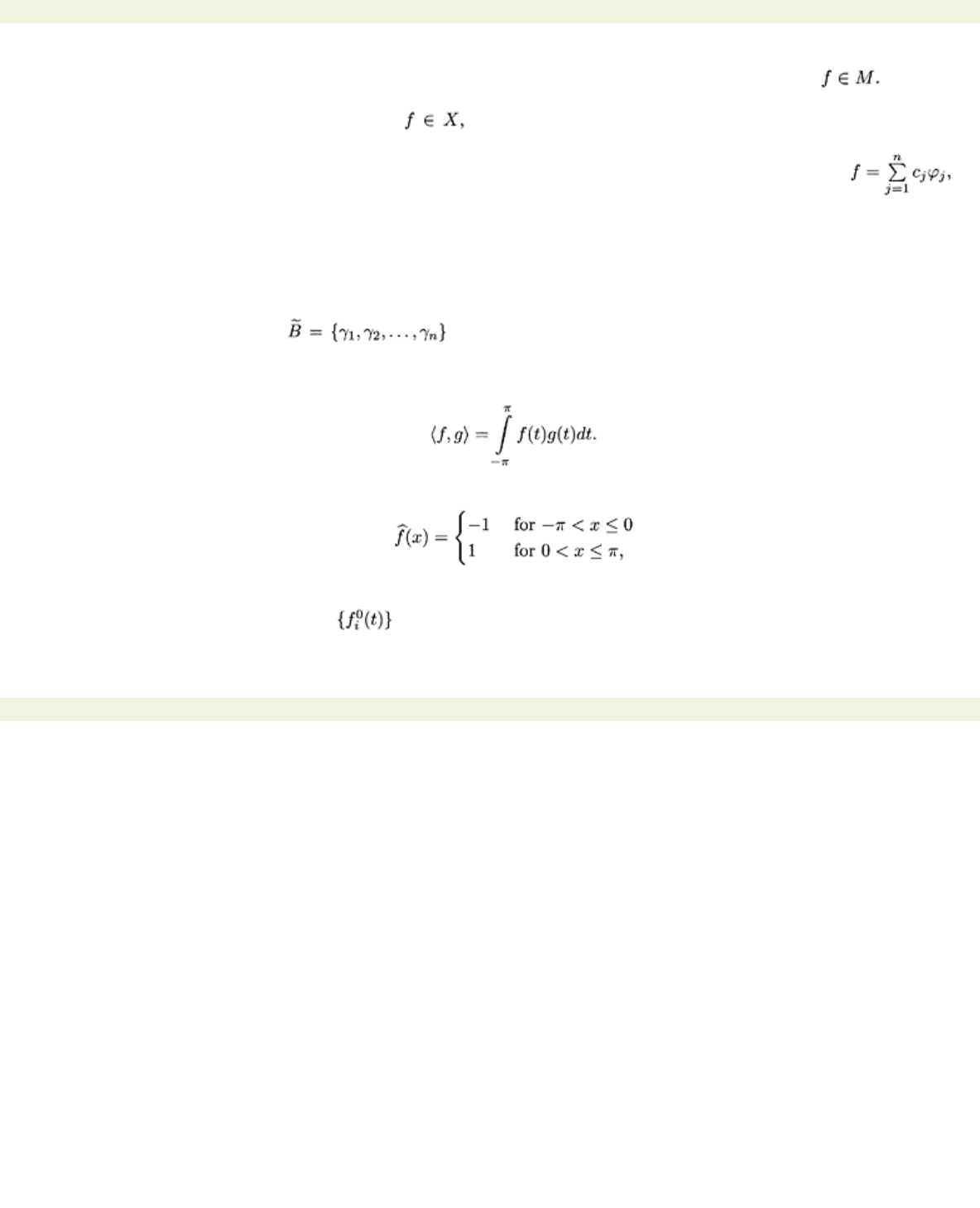
Suppose

is a finite-dimensional subspace of an inner product space, and suppose What is

the orthogonal projection of

onto

2.24)

Let

be an inner product space. For let

be the orthogonal complement of

. What is the

orthogonal projection of

onto

2.25)

Suppose

is an inner product space with an orthogonal basis

B={φ

, φ

...,

φn}.

Let

and let

C={φi

(1)

, φi

(2)

…

, φi(k)}

be a subset of

. Find

Pf,

the orthogonal projection of

onto

=span

2.26)In an inner product space

let

B={φ

, φ

…

, φn}

be a basis for the subspace

. Define a

sequence of vectors γ1, γ2,…, γn as follows:

γ1=

=φ

j−Pj−

φj, j=

2, 3, …

where

Pj−

φj

is the orthogonal projection of

φj

onto span{γ1,

γ2,...,γ

−1}. Prove that is an orthogonal basis for

. [This recipe for finding an

orthogonal basis is called the Gram-Schmidt process.]

2.27)Let

be the subspace of

(R)

consisting of all real-valued functions with period 2π with the inner

product

i) Verify that the collection

{sin

, sin 2

, sin 3

} is orthogonal,

ii) Let

be the periodic extension of

and find the projection of

onto the space spanned by the collection

iii) Sketch the graphs of

and the projection found in ii) on the same axes.

2.28)

Given

continuous functions and

distinct points

{tj},

show that if the

N×N

matrix

with

entries

Aij=fi(tj)

< previous page page_42 next page >

page_43

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_43.html[22/02/2009 23:51:35]

< previous page page_43 next page >

Page 43

is nonsingular, then the functions are linearly independent. Use the example

(t)

(1−

) and

(t)

2(1−

), and

1=0 and

2=1 to show that if the matrix

{fi(ti)}

is singular, then we cannot conclude anything about the linear dependence of

{fi(t)}

2.29)Suppose

{fi(t)}

is a set of

functions, each of which is

N−

1 times continuously differentiate on (0,

2). Show that if the

matrix

with entries

is nonsingular at some point

then the functions

{fi(t)}

are linearly independent. Use the

example

fi(t)=

max{(1−

)3, 0},

(t) =

max{0, (

t−

1)3} to show that if

is singular, then we can

conclude nothing about linear dependence. (Note: The determinant of the matrix

is known as the

Wronskian of the functions

{fi(t)}

< previous page page_43 next page >

page_44

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_44.html[22/02/2009 23:51:36]

< previous page page_44 next page >

Page 44

This page intentionally left blank.

< previous page page_44 next page >

page_45

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_45.html[22/02/2009 23:51:37]

< previous page page_45 next page >

Page 45

Chapter 3

Sturm—Liouville Problems

Many of the problems to be considered later will require an approximation of given functions in terms of

eigenfunctions of an ordinary differential operator. A well-developed eigenvalue theory exists for so-

called Sturm-Liouville differential operators, and we shall summarize the results important for the

solution of partial differential equations later on. However, in many applications only very simple and

readily solved eigenvalue problems arise which do not need the generality of the Sturm-Liouville theory.

We shall consider such problems first.

3.1 Sturm-Liouville problems for

The simplest, but also constantly recurring, operator is

defined on the vector space

2(0,

) of twice continuously differentiate functions on the interval (0,

or on some subspace

2(0,

) determined by the boundary conditions to be imposed on

Henceforth

will denote the domain on which is to be defined. In analogy to the matrix eigenvalue

problem

for an

matrix

we shall consider the following problem:

Find an eigenvalue

and all eigenfunctions (=eigenvectors) which satisfy

(3.1)

As in the matrix case the eigenvalue may be zero, real, or complex, but the corresponding eigenfunction

must not be the zero function. Note that if is an eigenvector, then for

≠0 is also an eigenvector.

< previous page page_45 next page >

page_46

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_46.html[22/02/2009 23:51:38]

< previous page page_46 next page >

Page 46

The domain on which is defined has an enormous influence on the solvability of the eigenvalue

problem. For example, if

2(0,

), then for any complex number

the equation

has the two linearly independent solutions

for

≠0 where and denote the two roots of

2−

=0, and

for

=0. Hence any number

is an eigenvalue and has two corresponding eigenfunctions. On the other

hand, if then for any

the only solution of

is the zero solution. Hence there are no eigenvalues and eigenvectors in this case.

The subspaces

2(0,

) of interest for applications are defined by the so-called Sturm-Liouville

boundary conditions

(3.2)

For example, in case iii)

subspaces consist of all functions such that and are

defined and

< previous page page_46 next page >

page_47

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_47.html[22/02/2009 23:51:39]

< previous page page_47 next page >

Page 47

We note that the first nine boundary conditions represent special cases of the general condition

(3.3)

for real

αi, βj

such that

The boundary condition x) is associated with periodic functions defined on the line. In each case the

subspace

will consist of those functions in

2(0,

) which are continuous or continuously differentiable

at 0 and

and which satisfy the given boundary conditions.

For several of these boundary conditions we can give explicitly the eigenvalues and eigenfunctions. To

see what is involved let us look at the simple case of

=0, then and the boundary conditions require

2=0 so that hence

≠0

is not an eigenvalue. For

≠0 the differential equation has again the general solution

The two boundary conditions require

or in matrix form

This system has a nontrivial solution

, c

)

=(1, −1) if and only if the determinant

f(μ)

of the

coefficient matrix is zero. We need

This can be the case only if

i.e., if

< previous page page_47 next page >

page_48

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_48.html[22/02/2009 23:51:39]

< previous page page_48 next page >

Page 48

for a nonzero integer

. Hence there are countably many eigenvalues

with corresponding eigenfunction

Since eigenfunctions are determined only up to a multiplicative constant, we can choose so that

The above calculation would have been simpler had we known a priori that the eigenvalue has to be

real and nonnegative. In that case complex numbers and functions can be avoided as we shall see

below. For the algebraic sign pattern of the coefficients in the boundary conditions of all of the above

ten eigenvalue problems this property is easy to establish.

Theorem 3.1

The eigenvalues of

(3.1)

for the boundary conditions

(3.2i–x)

are real and nonpositive.

Proof. If is an eigenvalue-eigenvector pair then

Integration by parts shows that

For each of the ten cases above the boundary terms either vanish or are real and nonpositive. For

example, if

2≠0 in (3.3), then

Hence

which implies that

is real and nonpositive.

Since the eigenvalue is real, it follows that the real and imaginary part of any complex-valued

eigenfunction must satisfy the eigenvalue equation. Hence the eigenfunctions may be taken to be real

so that the conjugation in the integrals can be dropped.

< previous page page_48 next page >

page_49

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_49.html[22/02/2009 23:51:40]

< previous page page_49 next page >

Page 49

Theorem 3.2

The eigenfunctions of

(3.1), (3.2)

corresponding to distinct eigenvalues are orthogonal in

2(0,

Proof. Let

and be eigenvalues and eigenfunctions with

µm

≠

μn

. Then

If we integrate by parts and use the boundary conditions, we see that the righthand integral vanishes

so that

The computation of the eigenvalues and eigenvectors for the above cases is straightforward, at least in

principle. Since

≤0, we shall write

=−λ2

and solve

We know that the general solution of this equation is

(3.4)

(3.5)

We now have to determine from the boundary conditions for what values of λ we can find a nontrivial

solution. To introduce the required computations let us look at the simple cases (3.2ii) and (3.2x) before

considering the general case (3.3).

(3.2ii)

We see by inspection that λ=0 is not admissible because there is no nonzero eigenfunction of the form

(3.4). For λ≠ 0 the solution is given by (3.5).

The boundary conditions lead to

λc2=0

1 cos

λL

2 sin

λL

which can be written in matrix form as

< previous page page_49 next page >

page_50

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_50.html[22/02/2009 23:51:41]

< previous page page_50 next page >

Page 50

This linear system has a nontrivial solution if and only if the coefficient matrix is singular. This will be

the case if its determinant

f(λ)

is zero. Hence we need

f(λ)

=−λ

cos

for any integer

. It follows that there are count ably many values

A corresponding nontrivial solution is

, c

)

=(1, 0). Since eigenvectors are determined only up to a

multiplicative constant, we may set

The negative integers may be ignored because they yield the same eigenvalues and eigenvectors.

Next we shall consider periodic boundary conditions.

(3.2x)

By inspection we find that λ=

=0 is an eigenvalue with eigenfunction

0(x)=1.

For nonzero λ the boundary conditions applied to (3.5) lead to

The determinant is

The determinant will be zero if and only if

λL

nπ

Note that for each such A the matrix becomes the zero matrix so that we have two linearly independent

solutions for

, c

which we may take to be (1, 0) and (0, 1). Hence for each nonzero eigenvalue

there are two eigenfunctions

where λn=(2

nπ

. Note that formally

(x)

is the eigenfunction already known to us.

< previous page page_50 next page >

page_51

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_51.html[22/02/2009 23:51:42]

< previous page page_51 next page >

Page 51

Finally, let us consider the general case of (3.3). If λ=0, then substitution of (3.4) into the boundary

conditions leads to the system

Under the hypotheses on the data the determinant of the coefficient matrix

can vanish only if α2=β2=0 so that

Then For all other cases

=λ=0 is not an

eigenvalue. If λ≠0, then (3.5) must be substituted into (3.3). This leads to the following matrix equation

for the coefficients

1 and

For a nontrivial solution the determinant

f(λ)

of the coefficient matrix must be zero. This leads to the

condition

f(λ)

(α

2−

)

sin

λL

λ(α

) cos λL

=0. (3.6)

We note that

f(λ)

=0 implies that

f(−λ)

=0. If the matrix is singular, then

, c

)

(λα

, α

)

determines the coefficients of (3.5).

Simple solutions of

f(λ)

=0 arise in the special cases (3.2i–iv).

1=0 or

implies that

f(λ)

=0 whenever sin

λL

=0 or

nπ/L, n=

1, 2,…

1=0 or

=β

2=0

implies that

f(λ)

=0 whenever cos

λL

=0 or If

1>0 or

1>0 (boundary

conditions associated with convective heat loss, for example), then the roots of

f(λ)

no longer are given

in closed form but must be determined numerically. All we can say is that if

1>0, then the roots of

f(λ)

=0 approach the roots of sin

λL

as if

1=0, then the roots of

f(λ)

=0 approach the roots of

cos

λL

as In all cases we obtain countably many values

We can summarize the results of our discussion of the eigenvalue problem (3.1), (3.2) in the following

table, to which we shall refer repeatedly as we solve partial differential equations.

< previous page page_51 next page >