Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach
Подождите немного. Документ загружается.

page_72
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_72.html[22/02/2009 23:51:59]
< previous page page_72 next page >
Page 72
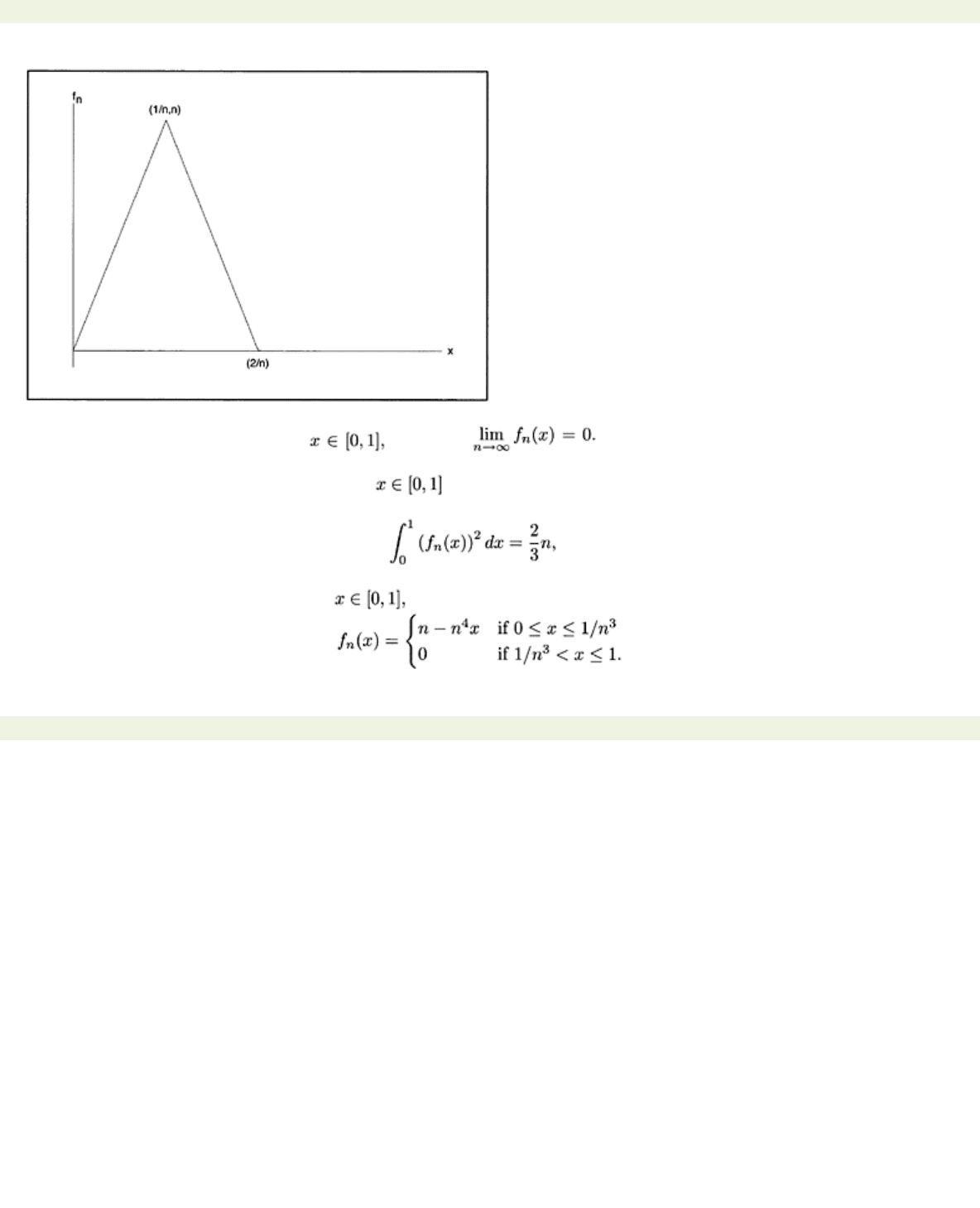
Figure 4.2:
{fn}
converges pointwise, but not uniformly or in the mean.
It should be clear that for each we have Thus the sequence
{fn}
converges
pointwise
to the function
f(x)
=0. Note that this sequence does not, however, converge
uniformly
to
f(x)=
0. In fact, for every
n,
there is an such that
|f
n
(x)−f(x)|≥n
.
Note that
which tells us that
{fn}
does not converge in the mean to
f
(with weight function
w(x)
=1, of course).
b) Next, for each integer n≥1 and let
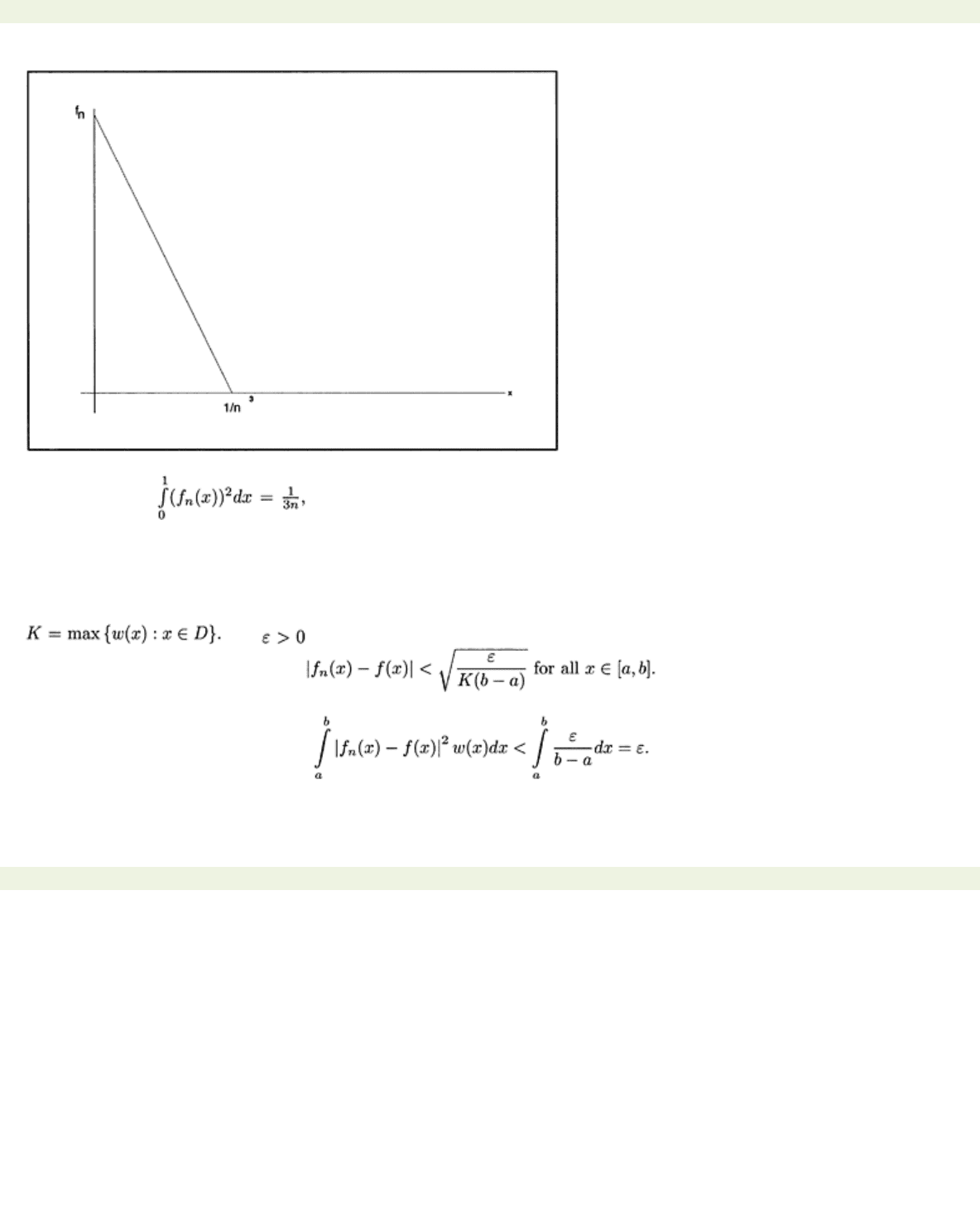
A picture is given in Fig. 4.3.
< previous page page_72 next page >
page_73
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_73.html[22/02/2009 23:52:00]
< previous page page_73 next page >
Page 73
Figure 4.3:
{fn}
converges in the mean, but not pointwise.
It is clear that
and so our sequence converges in the mean to
f(x)=
0. (Again, we have
w(x)
=1.) Clearly it does not converge to
f
pointwise or uniformly.
We see next that uniform convergence is the nicest of the three.
Theorem 4.7
Suppose the sequence {fn} of functions in L
2
(D, w), with domain D=[a, b], converges
uniformly to the function f. Then {fn} converges pointwise to f and also converges in the mean to f.
Proof. It is obvious that the sequence converges to
f
pointwise. For convergence in the mean, let
Let and choose n sufficiently large to ensure that
Then
Hence,
{fn}
converges in the mean to
f
.
Theorem 4.8
Suppose {fn} is a sequence of continuous functions on a domain D that converges
uniformly to the function f. Then f is also continuous on D.
< previous page page_73 next page >

page_74
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_74.html[22/02/2009 23:52:01]
< previous page page_74 next page >
Page 74
Proof. To show that
f
is continuous, let and let be given. Let
N
be sufficiently large to
ensure that
for all Now let
δ
be such that
for all
x
such that |
x−x
0
|<δ.
Then for
|x−x
0
|<δ
we have
4.3 Convergence of Fourier series
We know from Theorem 3.3 that for
the Fourier series of
f
converges in the mean to
f
. In
other words
where
(The coefficients
an
and
bn
are, of course, the Fourier coefficients.) In practice we generally need to
know more and are interested in conditions ensuring pointwise or uniform convergence of the series. In
this section are some of the most important results regarding convergence of Fourier series.
This first result is an immediate consequence of Proposition 4.3.
Proposition 4.9 (Bessel’s Inequality)
The next one follows directly from Corollary 4.5.
< previous page page_74 next page >

page_75
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_75.html[22/02/2009 23:52:01]
< previous page page_75 next page >
Page 75
Proposition 4.10 (Riemann’s Lemma)
Definitions A function
f
defined on the reals is piecewise continuous if it is continuous except for at
most a finite number of jump discontinuities on any finite interval. A function
f
is piecewise smooth if it
is piecewise continuous and on every finite interval has a piecewise continuous derivative except at a
finite number of points. Recall that a jump discontinuity of
f
at a point a is a point at which
f
is not
continuous, but both the one-sided limits
f(a−)
and
f(a+)
exist.
Example 4.11 a) The function from Example 4.1, the periodic extension the function
f(x)=x,
for −
π
≤ x ≤ π
, is piecewise smooth,
b) The function f defined by
is piecewise continuous (in fact, continuous), but is not piecewise smooth. There is no derivative at
x=
0
and for
x≠
0, we have
which has no one-sided limits at
x=
0. The derivative is thus not piecewise continuous.
We shall now cite the two main theorems on the convergence of Fourier series. The proofs are omitted
and may be found, e.g., in [4].
Theorem 4.12
If f is a piecewise smooth periodic function, then the Fourier series of f converges
pointwise to the function
In case
f
is continuous,
f(x+)=f(x−)
for every
x
and so the Fourier series converges to
f
. We can,
however, in this case say a lot more.
Theorem 4.13
If f is a continuous piecewise smooth periodic function, then the Fourier series of f
converges uniformly to f.
< previous page page_75 next page >

page_76
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_76.html[22/02/2009 23:52:02]
< previous page page_76 next page >
Page 76
Since the uniform limit of a sequence of continuous functions is continuous (Theorem 4.8), we know if
f
is not continuous, then the convergence cannot possibly be uniform.
Example 4.14 a) Let us find the Fourier series for the function
f(x)=x
on the interval [−π, π]
The Fourier series is
Now, what does the sum of this series look like? We simply apply Theo rem 4.13 to the periodic
extension
of
f
found in Example 4.1. At discontinuities of the extension (odd multiples of
π
), the limit
is simply 0.
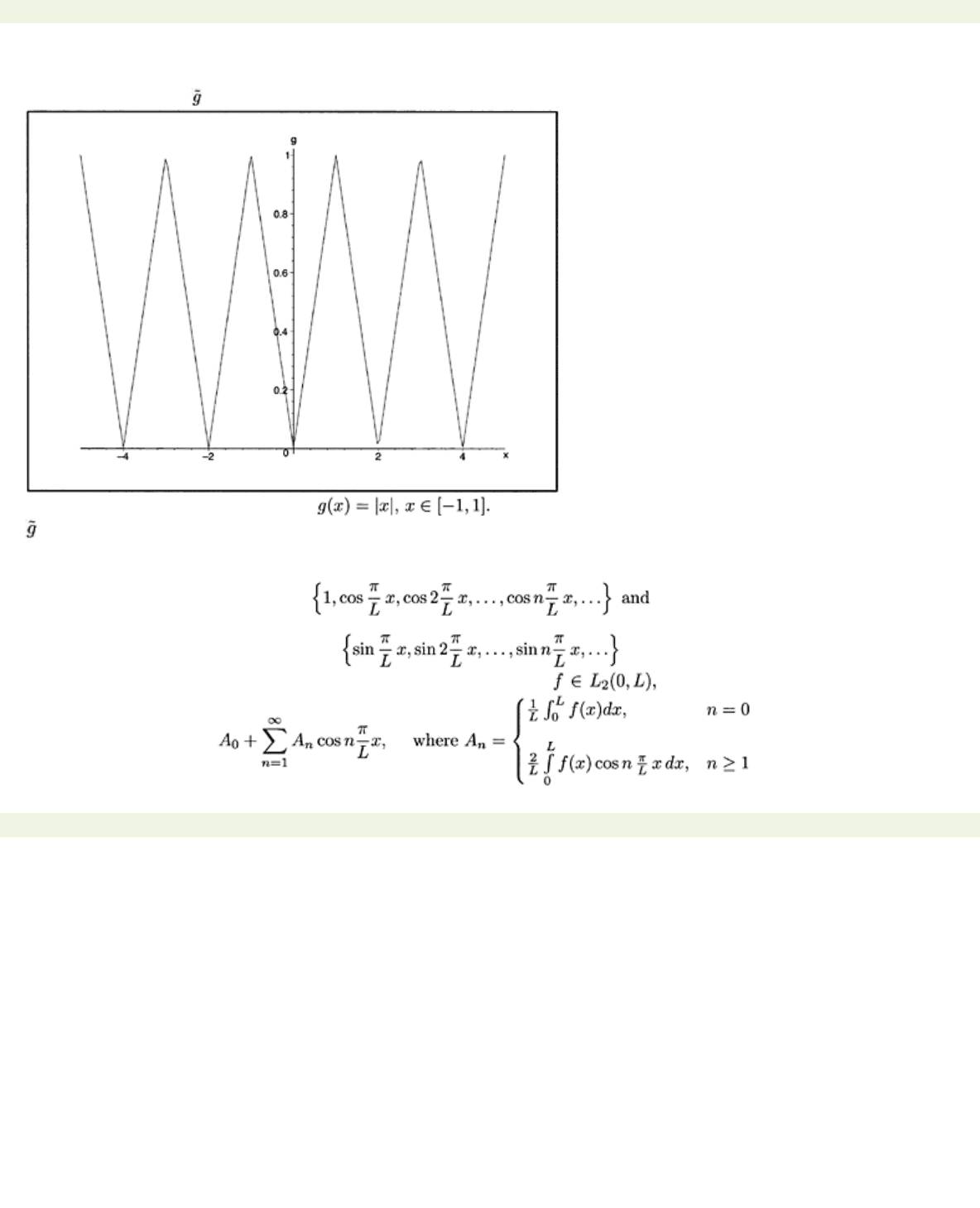
b) We shall find the Fourier series of the function
g(x)=|x|
on the interval [−1, 1].
Life can be made a bit simpler by noting that for
n≥
1
Then letting n=2
k
+1, we have the Fourier series
< previous page page_76 next page >
page_77
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_77.html[22/02/2009 23:52:03]
< previous page page_77 next page >
Page 77
Now, where does this series converge and what does the sum look like? Again, we simply look at the
periodic extension
of
g
. A picture is shown in Fig. 4.4.
Figure 4.4: Periodic extension of
is continuous and piecewise smooth so that the Fourier series of
g
converges uniformly to
g.
4.4 Cosine and sine series
We know from the Sturm—Liouville theory that
are both orthogonal sets in the space
L
2(0,
L
) and that for the series
< previous page page_77 next page >

page_78
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_78.html[22/02/2009 23:52:04]
< previous page page_78 next page >
Page 78
converges in the mean to
f(x)
as does the series
These are called, respectively, the Fourier cosine series of
f
and the Fourier sine series of
f
. These are
very important in the applications to follow.
Definitions Let f be a function denned on the interval 0
≤x≤L
and let be denned on −
L ≤ x ≤ L
by
The periodic extension of to the entire real line is called the even periodic extension of
f
. The periodic
extension of
f
given by
is called the odd periodic extension of
f
.
For
f
defined on 0
≤x≤L
observe that
and
It is clear from these that the Fourier cosine series of
f
is simply the Fourier series of the even periodic
extension
and the Fourier sine series of
f
is the Fourier series of the odd periodic extension
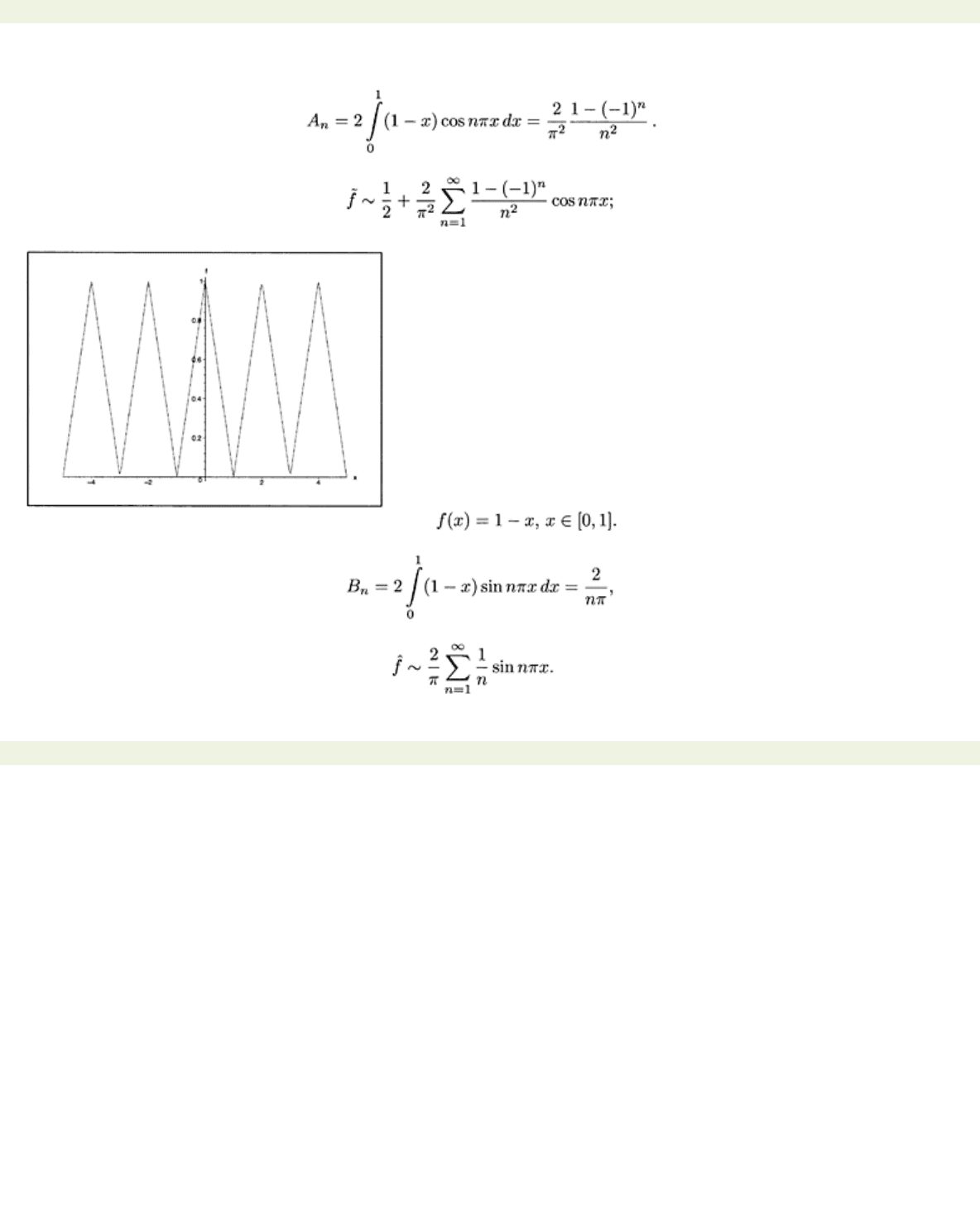
Example 4.15 Let f be defined by
f(x)
=1−
x
for 0 ≤
x
≤ 1.
a) First, we find the cosine series of
f,
< previous page page_78 next page >
page_79
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_79.html[22/02/2009 23:52:04]
< previous page page_79 next page >
Page 79
and we have
The cosine series is thus
and the graph of the sum of this series is given in Fig. 4.5.
Figure 4.5: Plot of the Fourier cosine series of
b) Now we find for the sine series of
f
.
and so the sine series is
The limit of this one at
x
≠2k,
k=
0, ±1,…, is shown in Fig. 4.6.
< previous page page_79 next page >

page_80
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_80.html[22/02/2009 23:52:05]
< previous page page_80 next page >
Page 80
Figure 4.6: Plot of the Fourier sine series of
Observe that both the cosine and the sine series converge to
f
on the interval 0<
x
<1, but the cosine
series converges uniformly, while the sine series does not.
4.5 Operations on Fourier series
It is clear that if
f
has Fourier coefficients
an
and
bn,
then the function
cf,
where
c
is a constant, has
Fourier coefficients
can
and
cbn.
Similarly, the coefficients of the sum of two functions are the sums of
the corresponding coefficients of the two functions. Here we consider more interesting operations on
Fourier series of functions. First, we give the integration of series.
Theorem 4.16
Suppose f is piecewise continuous and periodic with period
2
L. Then for all x it is true
that
where
is the Fourier series of f.
Proof. Let
F
be defined by
< previous page page_80 next page >

page_81
file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_81.html[22/02/2009 23:52:06]
< previous page page_81 next page >
Page 81
Then
F
is continuous, piecewise smooth and
F′(x)=f(x)
at the points of continuity of
f
. Moreover,
F
is
periodic with period 2
L
because
Thus the Fourier series of
F
converges uniformly to
F(x)
for all
x
where
For
n
≠0, integrating by parts gives
Hence
Now by the definition of
a
0
This gives
so that
< previous page page_81 next page >
