Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_52

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_52.html[22/02/2009 23:51:43]

< previous page page_52 next page >

Page 52

Table 3.1:

Eigenvalues and eigenvectors for and various boundary conditions Boundary Condition

Eigenfunction(s)

nπ/L

sin

λnx, n

=1, 2,…

ii) sin

λnx, n

=0, 1,…

iii) cos

λnx, n

=0, 1,…

iv)

nπ/L

cos

λnx, n

=0, 1,…

nπ/L

sin

λnx, n

=1, 2,…

nπ/L

cos

λnx, n

=0, 1,…

v–ix)The remaining cases require a solution of (3.6) for the various combinations of

αi

and

βj

The corresponding eigenfunction is always

Replacing

by −

does not change the eigenvalue and only changes the algebraic sign of the

eigenfunction. Hence we can restrict ourselves to the positive roots of

f(λ)

=0.

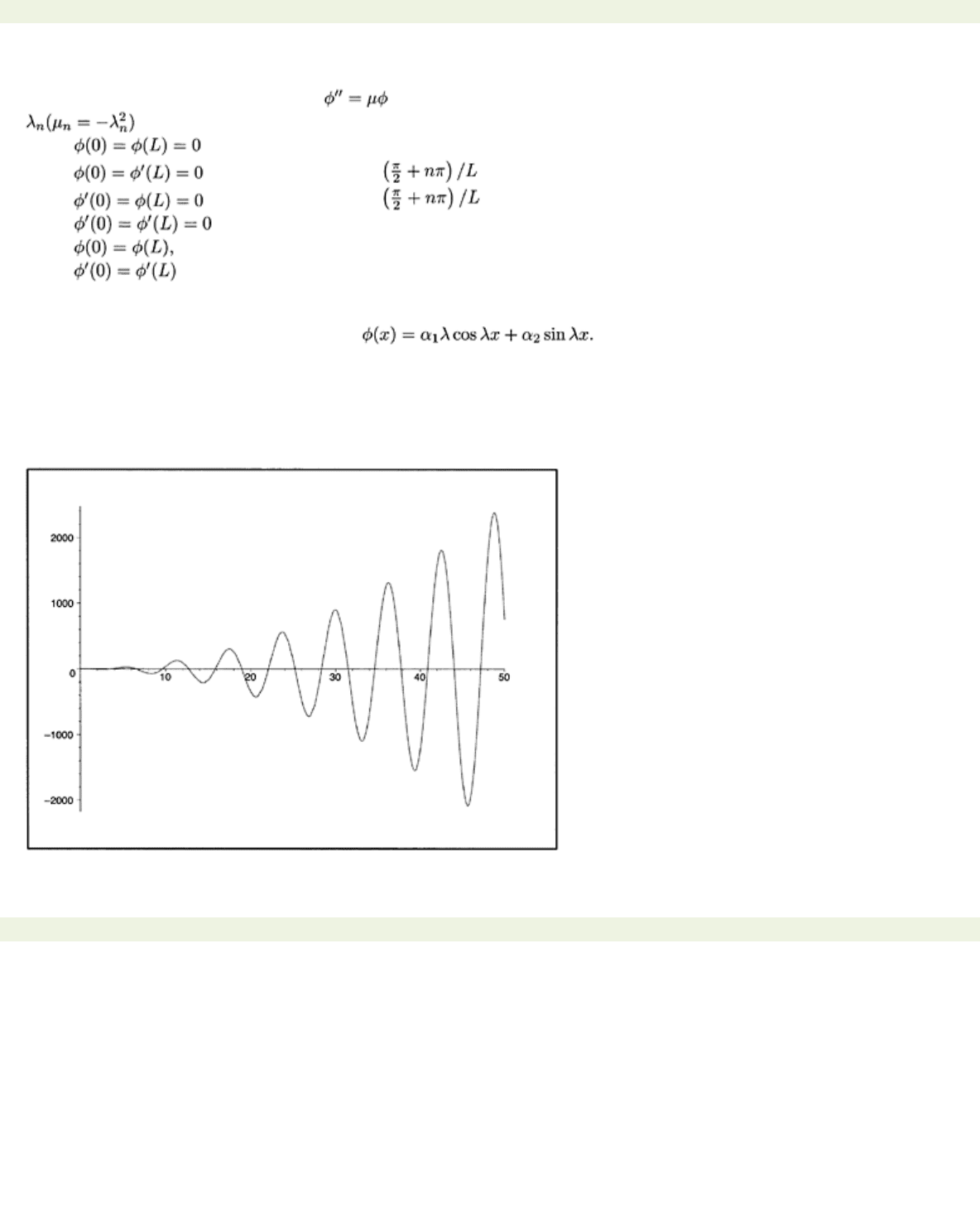
For illustration we show in Fig. 3.1a a plot of

f(λ)

vs.

and in Fig. 3.1b a plot of the eigenfunctions

corresponding to the first two positive roots of

f(λ)

=0 when

=α

=β

=L=

1. Note that these

functions do not have common zeros or a common period. However, they are orthogonal in the mean

square sense as guaranteed by Theorem 3.2.

Figure 3.1: (a) Plot of

f(λ)

of (3.6) for

=α

=L=

1. The first two roots are

1=1.30654,

2=3.67319.

< previous page page_52 next page >

page_53

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_53.html[22/02/2009 23:51:43]

< previous page page_53 next page >

Page 53

Figure 3.1: (b) Plot of

We point out that if the sign conditions of (3.3) are relaxed, then the eigenvalues of

remain real and the eigenfunctions corresponding to distinct eigenvalues are still orthogonal. However,

some eigenvalues can be positive and eigenfunctions may now involve real exponential as well as

trigonometric functions (see Exercise 3.13).

3.2 Sturm—Liouville problems for

For the simple operator we could exhibit countably many eigenvalues and the corresponding

eigenf unctions. For more general variable coefficient operators explicit solutions are no longer available;

however, for the class of Sturm-Liouville eigenvalue problems a fairly extensive theory now exists with

precise statements about the existence of eigenvalues and eigenfunctions and their properties. We shall

cite the aspects which are important for later applications to partial differential equations.

A typical Sturm-Liouville eigenvalue problem is given by

(3.7)

< previous page page_53 next page >

page_54

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_54.html[22/02/2009 23:51:44]

< previous page page_54 next page >

Page 54

where

p′, g,

and

are real continuous functions on the interval [0,

], where

p(x)

is nonnegative on [0,

] and where

w(x)

is positive except possibly at finitely many points,

is a weight function of the type

introduced in Chapter 2. We shall impose on (3.7) the boundary conditions

where the coefficients satisfy the same conditions as in (3.3). If

(0) and

p(L)

are positive, we have

exactly (3.3); but if, for example,

(0)=0, then and are merely assumed to exist,

is again

called the eigenvalue of problem (3.7) and is the corresponding eigenfunction. Assuming their

existence we can readily characterize their properties.

is an eigenvalue with corresponding eigenvector then it follows from integration by parts applied

that

The boundary conditions again guarantee that the first term on the left is real and nonpositive so that

is real and

A real eigenvalue implies that the real and imaginary parts of any complex valued eigenfunctions

themselves are eigenfunctions so that again we may restrict ourselves to real vector spaces.

If we now assume that

and are eigenvalue-eigenvector pairs for distinct eigenvalues,

then

Integration by parts shows that

< previous page page_54 next page >

page_55

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_55.html[22/02/2009 23:51:45]

< previous page page_55 next page >

Page 55

The boundary conditions imply that the integral vanishes. Thus we can conclude that

where (,) is the inner product on

2(0,

L, w

Until now we have either calculated explicitly the eigenvalues and eigenfunctions, or we have assumed

their existence. The significance of the SturmLiouville problem (3.7) is that such assumption is justified

by the following theorem [16].

Theorem 3.3

Assume that in

(3.7)

the coefficients are continuous and that p, w

[0,

Then

there are countably many real decreasing eigenvalues {μn} and eigenfunctions

with

For each eigenvalue there are at most two linearly independent eigenfunctions which may be chosen to

be orthogonal. All eigenfunctions constitute an orthogonal basis of the inner product space L

2(0,

L, w

)

and for any

where

is the orthogonal projection of f onto

The theorem asserts that

2(0,

L, w

) contains countably many orthogonal elements Since any

finite number of these elements are necessarily linearly independent, we see that

2(0,

L, w

) is an

infinite-dimensional inner product space. The definition of basis in Chapter 2 must be broadened to

apply in an infinite-dimensional vector space

. Let

{xn}

be a sequence of elements of a normed linear

space

. We say that

{xn}

is a basis of

if any finite set of these vectors is linearly independent and for

any there is a sequence of scalars

{an}

such that

For the orthogonal basis of Theorem 3.3 the linear combinations may be taken to be the orthogonal

projections.

Throughout the following chapters we are going to approximate given functions by their orthogonal

projections onto the span of finitely many eigenfunctions of Sturm-Liouville problems. It is reassuring to

know that the approximations converge as we take more and more eigenfunctions. Unfortunately, such

< previous page page_55 next page >

page_56

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_56.html[22/02/2009 23:51:46]

< previous page page_56 next page >

Page 56

convergence can be painfully slow. Let us take the function

f(x)

=1 in

2(0, 1) and project it into the

span of eigenfunctions {sin

nπx

} of case i) in Table 3.1. From Theorem 3.3 we know that ||1−

1||→0

→∞. A simple calculation yields

Computed values (in single precision) are

10 .20099

100 .06366

1000 .02013

10000 .00815

That is about as close as we can come numerically. On the other hand, for

f(x)

(1−

) we obtain

10 .00019

20 .00009

The next chapter gives some insight into why

is difficult and is easy to

approximate in this setting. Here we merely would like to point out that when in later examples we

solve the Dirichlet problem

then the simple source term

generally will make the mechanics of solving the problem easier

but does not favor convergence of the approximate solution to the analytic solution.

≥0 and

(0)

(1)=0 or

0 at finitely many points, then we have a singular Sturm-Liouville problem.

The eigenvalue problem for Bessel’s equation in Chapter 6 is a typical example of a singular problem.

The theory for such problems becomes more complicated but in the context of separation of variables it

is safe to assume that

and

are such that the conclusion of Theorem 3.3 remains valid. In particular,

this means that we always expect that

< previous page page_56 next page >

page_57

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_57.html[22/02/2009 23:51:47]

< previous page page_57 next page >

Page 57

where

is an arbitrary function in

2(0,

L, w

) and γn is the Fourier coefficient

with

Next we observe that the general eigenvalue problem

(3.8)

can be put into Sturm-Liouville form (3.7) if there is a weight function

w(x)

such that

can be written in the form of (3.7). A comparison shows that we would need

a(x)w(x)=p(x)

b(x)w(x)=p′(x)

so that

(aw)′=bw.

a(x)

≠0 on [0,

], then we can write

and find that for any

is an admissible weight function. Hence eigenfunctions of (3.8) can be found such that they form an

orthogonal basis of

2(0,

L, w

). For example, consider the eigenvalue problem

(3.9)

We see that

and that the problem can be rewritten as

< previous page page_57 next page >

page_58

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_58.html[22/02/2009 23:51:48]

< previous page page_58 next page >

Page 58

The above discussion immediately yields that eigenvalues (should they exist) are negative and that

eigenfunctions corresponding to distinct eigenvalues are orthogonal in

(0, 1,

2).

Throughout this text eigenvalue problems like (3.8) are useful for solving partial differential equations

only if one can actually compute the eigenvalues and eigenfunctions. As a rule that is a difficult if not

impossible task since there is no general recipe for solving ordinary differential equations with variable

coefficients. When confronted with an unfamiliar differential equation, about the only choice is to check

whether the equation is listed in handbooks of solutions for ordinary differential equations such as [12],

[18]. Fortunately, (3.9) appears as equation 2.101 in [12] and is solvable by elementary means. We

rewrite the equation as

so that

It is straightforward to verify that

while

Hence

where {λn} are the solutions

which leads to

Since

f(nπ)f

((

+1)

)<0, there is a root in each subinterval (

nπ,

(

+1)

), but its value can only be

found numerically.

Many applications of separation of variables lead to ordinary differential equations which are solved in

terms of Bessel functions (see Examples 6.10, 7.5, 8.5, 9.8). Bessel functions belong to the class of

“special functions” studied in such texts as [1] (for real arguments) and [13] (for complex arguments).

Because of the ubiquity of Bessel functions, we include here for easy reference a general second order

ordinary differential equation which can be solved in terms of Bessel functions. We cite from [21].

< previous page page_58 next page >

page_59

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_59.html[22/02/2009 23:51:48]

< previous page page_59 next page >

Page 59

If (1–

)2≥4c and if neither

d, p,

nor

is zero, then, except in the obvious special cases when it reduces

to Euler’s equation, the differential equation

(3.10)

has the general solution

where

<0,

Jv,

and

are to be replaced by

and

Kv,

respectively. If

is not an integer,

and

can

be replaced by

J−v

and

I−v

if desired.

The definitions and properties of the various functions just cited are discussed in the above sources (see

also Example 6.10). The manipulation and evaluation of these functions have become routine in

programming environments like Maple, Mathematica, and Matlab.

3.3 A Sturm—Liouville problem with an interface

We shall conclude our discussion of eigenvalues for equation (3.8) by considering the following

generalization of the simple equation (3.1):

where

for given positive constants ai and a given interface

. At

0 and

x=L

the function may be subject

to any of the boundary conditions of Table 3.1, but for definiteness we shall choose here

the eigenfunction is required to satisfy an interface condition of the form

< previous page page_59 next page >

page_60

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_60.html[22/02/2009 23:51:49]

< previous page page_60 next page >

Page 60

where

1 and

2 are given positive constants. Interface conditions like these arise when the method of

separation of variables is applied in composite media (see Example 6.11).

Let us introduce the piecewise constant weight function

and the inner product

Then

We integrate the left side by parts over [0,

] and

[X, L]

and obtain

The boundary and interface conditions imply that the boundary and interface terms drop out or cancel.

Hence

so that an eigenvalue of this problem is real and nonpositive and has a real eigenfunction. Similarly, it

follows from integration by parts applied to

that the left integral vanishes so that eigenf unctions corresponding to distinct eigenvalues are

orthogonal in

2(0,

L, w

). Eigenvalues and eigenfunctions can be found explicitly. We observe first that

μ=0

would lead to

< previous page page_60 next page >

page_61

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_61.html[22/02/2009 23:51:50]

< previous page page_61 next page >

Page 61

The boundary conditions require that

2=0. The interface conditions

X=d

2=0

imply that

0 and show that there is no nonzero solution corresponding to

μ=

0. Let us then write

−

λ2 for λ≠0.

Then any solution of our interface problem must be of the form

The boundary conditions allow us to write

The interface conditions lead to

A nonzero solution results if the determinant

(λ) of the coefficient matrix is zero. Hence we need roots

This expression can be rewritten in the form

We see that for

=α

2 and

2 the eigenvalue condition reduces to that of ii) in Table 3.1. This is

the correct behavior because the solution is now twice continuously differentiable at

so that the

location of

should not have any influence. The eigenfunction corresponding to any nonzero root of this

equation is

< previous page page_61 next page >