Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_32

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_32.html[22/02/2009 23:51:26]

< previous page page_32 next page >

Page 32

Now simply choose the scalar

Then

Hence

which shows that

must be the orthogonal projection of

onto

Example 2.10 In the plane

let and let

= span

a) With the usual inner product, which induces the usual Euclidean length of vectors, the projection

of onto

Then is the point on the line 5

−3

=0 that is closest to (1,2) and the vector is

perpendicular to all vectors

b) In the plane with the inner product of Example 2.3b, the projection of onto the subspace

Then

and so

c) In the space of all continuous real-valued functions on the interval [−1, 1] with the inner product

let

be the subspace consisting of all polynomials of degree ≤2. Let us find the orthogonal projection

onto

defined by

The obvious basis for M is {1,

x, x

2}. Then

< previous page page_32 next page >

page_33

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_33.html[22/02/2009 23:51:27]

< previous page page_33 next page >

Page 33

The coefficient matrix

for the linear system to be solved for the coordinates of the projection

P f

We now know that

Pf(x)=α

3, where

Thus α1=3/32, α2=1/2, and α3=15/32. The projection of

is then

We have found the “best” approximation to

in the sense that of all quadratic functions

this is the

one that gives the smallest value of

This is sometimes called the

least squares

approximation.

Pictures of both

and

on the same axes are shown in Fig. 2.1.

Figure 2.1: Least squares approximation of

f(x)

=max{0,

} on [−1, 1] with a quadratic polynomial.

< previous page page_33 next page >

page_34

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_34.html[22/02/2009 23:51:28]

< previous page page_34 next page >

Page 34

2.3 Important function spaces

It is easy to see that the collection of all continuous (real- or complex-valued) functions defined on an

interval

[a, b]

with the usual definition of addition is a linear space, traditionally denoted

C[a, b]

. It

becomes an inner product space if we define

A so-called weight function

may also be introduced. If the function

is real valued and continuous on

[a, b]

and such that

w(x)

≥0 for all

and

w(x)

=0 at a finite set of points, then it is easy to see that

is also an inner product for our space. The restriction on

w(x)

guarantees that for

f≠

Spaces of continuous functions are useful, but they are not sufficiently large for subsequent applications

because they do not contain certain important types of functions—step functions, square waves,

unbounded functions, etc. The spaces with which we shall be primarily concerned are the so-called

spaces. Specifically, suppose

is a real interval,’ finite or infinite, and

is a weight function as defined

above. Then

(D, w)

is the collection of all functions for which |

is integrable. It can be shown

that this is indeed a vector space and that with the definition

we have almost an inner product space: “almost” because with this definition, it is possible to have

for a function

other than the zero function. For example, with

w(x)=

[0, 1], and f

given by

(0)=1 and

f(x)

=0 for all

≠0, we have ||

||=0. To ensure we have an inner product, we

simply say that two functions

and

are “equal” if

Here by “integrable” we mean integrable in the sense of Lebesgue, but the reader unfamiliar with this

concept need not be concerned. In the applications in the sequel, the integrals encountered will all be

the usual Riemann integrals of elementary calculus.

Note. In case the weight function

w(x)

=1, we abbreviate

(D, w)

with

(D)

< previous page page_34 next page >

page_35

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_35.html[22/02/2009 23:51:29]

< previous page page_35 next page >

Page 35

The essence of this discussion remains the same when we consider real- or complex-valued functions of

several variables; i.e., when the domain

is a subset of

Given

then its orthogonal projection onto a finite-dimensional subspace is just a least

squares approximation (as in Example 2.10c), but with respect to the weight function

The weight

function is sometimes introduced to improve the fit of the approximation in the region where

is large,

but in this text its role is usually to make the basis spanning

an orthogonal basis as we shall see in

the next chapter.

Example 2.11 a) Let

[0, 1]. Then in the space

(D),

it is straightforward to see that the set

{1,

cos π

, cos 2π

, cos 3π

} is orthogonal. We shall find the projection

of the step function

given by

f(x)

=−1+2

(

–.5),

onto the subspace

=span

Here

is the Heaviside function defined by

Since

is orthogonal, we obtain

b) Let us again project

onto span

but in the space L2

(D, w),

where

w(x)=x

(1−

). The inner product

is now given by

and the collection

is no longer orthogonal. The projection

in this case is

Pf=α

1+α2 cos π

+α3 cos 2π

+α4 cos 3π

< previous page page_35 next page >

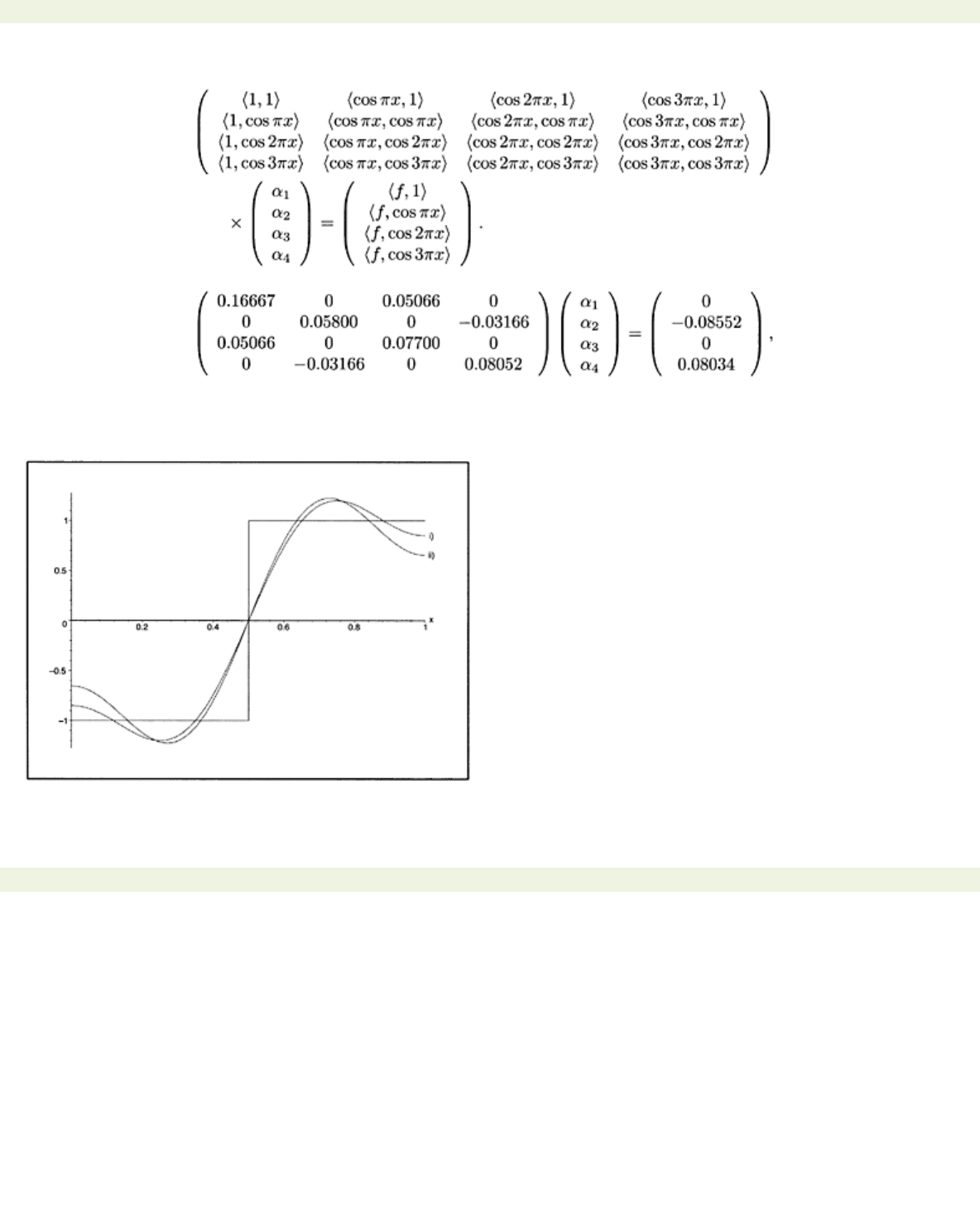
page_36

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_36.html[22/02/2009 23:51:29]

< previous page page_36 next page >

Page 36

where

After some computation, we have

and

3=0,

2=−1.1840, and

4=0.53224.

Our projection

thus becomes

Pf=

−1.1840 cos π

+0.53224 cos 3π

A picture of

the projection from a) and the projection just found are shown in Fig. 2.2.

Figure 2.2: Orthogonal projections of

f(x)

=−1+2

(

x−

.5). i) in

2(0, 1) and ii) in

2(0, 1,

(1−

)).

Finally, we note that on occasion for a function of several variables we shall consider a subset of them

as fixed parameters and compute projections with

< previous page page_36 next page >

page_37

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_37.html[22/02/2009 23:51:30]

< previous page page_37 next page >

Page 37

respect to the remaining variables. For example, let

F(x, t)

be a function defined on a set

where

and

are intervals. Suppose that for each Let

Then we write

depends smoothly on

then it follows from the computation of the

αj(t)

that these coefficients

likewise will depend smoothly on the parameter

In approximation theory the function

, t)

is interpreted as an abstract function defined on [0,

] with

values in

(D, w).

The approximation

PF(

,t)

then is the associated abstract function with values in the

finite-dimensional subspace

. However, we shall be content to consider

simply as a parameter.

Example 2.12 Let

F(x, t)=cos(xt)

for all where

is the interval [0, 1] and

is the entire

real line. Then for each real

it is clear that We know that {1, cos π

, cos 2π

, cos

3π

} is orthogonal. Let us find the projection of

onto

=span {1, cos π

, cos 2π

, cos 3π

From Example 2.11 a) we know that

Thus

This appears at first glance to contradict the statement that the coefficients should be differentiate

functions of

but notice that each term of the sum has a limit at the zero of the denominator. If, as we

usually do, define them

< previous page page_37 next page >

page_38

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_38.html[22/02/2009 23:51:31]

< previous page page_38 next page >

Page 38

to be equal to this limit at the value of

at which the expression is undefined, computation will show the

resulting functions to be differentiable. Look for instance at

(t),

the coefficient of cos π

. Then

The same limit is obtained as

→−π and so

is continuous at

=±

. In fact, since sin

t/t

is infinitely different iable at

=0 one can readily show that

α2(t)

has derivatives of all orders there.

We make the observation that even though

F(x, t)

may be well behaved it often is not possible to find

PF(x, t)

explicitly as a function of

. A projection of

F(x, t)

onto span

{φ

1,…,

φN}

requires the coefficient

which is available only if can be evaluated analytically or numerically for arbitrary

. For a

function like

this is generally not possible. On the other hand, for a given value

* the integral

will always be assumed known, if not analytically, then at least numerically.

We shall conclude with a result which has the same flavor as Theorems 2.8 and 2.9 and which is used

in Example 7.7.

Theorem 2.13

Let X be an inner product space. Let {φ

…,

φN} be a set of N linearly independent

elements of X. Then the “smallest” solution (i.e., the minimum norm solution) of the N linear equations

belongs to

span

{φ

…,

φN}.

Proof. We show first that the equations have a unique solution

. If we substitute

< previous page page_38 next page >

page_39

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_39.html[22/02/2009 23:51:32]

< previous page page_39 next page >

Page 39

into the linear equations, we find that the

{αj}

must solve the the matrix equation

where

We know from Proposition 2.7 that

is nonsingular so that there is a unique solution

Suppose there is another solution Then

Since

and

satisfy the same equations, it follows that

Hence

for any other solution

Exercises

2.1)

Find the equation of the form

spanned by the vectors and

2.2)Prove or disprove: the functions {sin

cos

sin(

+5)} are linearly independent.

2.3)

Let

be complex Euclidean space; i.e., the space of all

-tuples of complex

numbers with usual definitions of vector addition and scalar multiplication. Show that each of the

following defines a norm on

Cn:

ii)

2.4)Let

be the vector space of all continuous complex-valued functions

on the interval [0, 1]. Show

that each of the following defines a norm on

ii)

2.5)Prove Proposition 2.2.

< previous page page_39 next page >

page_40

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_40.html[22/02/2009 23:51:33]

< previous page page_40 next page >

Page 40

2.6)

On complex Euclidean space

Cn,

define where and

Verify that this defines an inner product on

2.7) Verify Example 2.3c.

2.8)

Show that in an inner product space

the vector is orthogonal to every vector in

and it is the

only element of

having this property.

2.9) Let

be an inner product space and let Prove that the set

of all orthogonal to

is a

subspace of

. (This subspace is called the orthogonal complement of

2.10)

Let

i) Find the orthogonal complement of with respect to the usual dot product.

ii) Find the orthogonal complement of with respect to the inner product described in Example

2.3b.

2.11)

Let

be a subspace of an inner product space

and let be given by

i) Show that

is a subspace of

ii) Show that

[The subspace

is called the orthogonal complement of

thus the orthogonal complement of a

vector

defined in Exercise 2.9 is in this sense the orthogonal complement of the subspace

spanned by

2.12)

2 let Find

where the norm is the one induced by the usual dot product (Example 2.3a);

ii)

where the norm is the one induced by the inner product described in Example 2.3b.

2.13)In

show that

defines a norm. For

and find and

< previous page page_40 next page >

page_41

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_41.html[22/02/2009 23:51:34]

< previous page page_41 next page >

Page 41

2.14)

Find the root mean square of on the interval [0,

2.15)

Suppose

is an inner product space. Show that for it is true that

2.16)Is every norm induced by some inner product?

2.17)

In an inner product space, show that if then This is called the

Pythagorean theorem. Why?

2.18)Let 0=

1<…<

tN=L

define a partition on [0,

] with

tn+

1−

= Δ

. Define the mapping

from

[0,

] into

Tf=(f(t

), f(t

…,

f(tN)).

i) Show that

is a linear transformation,

ii) Show that

is not invertible.

iii) Find an inner product

on such that

for small Δ

2.19)

In the Euclidean plane with the usual norm, given a point

find the point on the line

y=ax closest by projecting the point onto the line.

2.20)In Euclidean three-space with the usual norm, find the point in the plane 2

y−

0 that is

closest to the point (0, 0, 5).

2.21)

Find the point on the line described by the vector function that is closest to

the point (1, 4, −2).

2.22)

Find the polynomial of degree ≤2 that is the best approximation to in the sense that

among all such polynomials q it minimizes

Sketch the graphs of your approximation and

on the same axes.

< previous page page_41 next page >