Buschow K.H.J. (Ed.) Concise Encyclopedia of Magnetic and Superconducting Materials
Подождите немного. Документ загружается.


6. Microscopic Origin of Magnetostriction
Within the model of localized electron ferro-
magnetism, two microscopic mechanisms are the or-
igin of magnetostriction: exchange interaction be-
tween spins, and interaction of a given spin with its
local electric field via the spin–orbit coupling. Al-
though it may provide some good clues even in the
case of transition metals and alloys, the localized
electron model is inadequate for these materials and
must be replaced by the band magnetism model. In
this model magnetostriction appears as an interaction
between the strain and the spin-dependent band
structure (du Tremolet de Lacheisserie 1993).
6.1 Spin–Spin Interaction
The dependence of the isotropic Heisenberg exchange
on distance between neighboring spins leads to a vol-
ume magnetostriction which is generally negative and
therefore leads to an enhancement of the lattice ther-
mal expansion. This is the ‘‘normal’’ situation, ob-
served, for example, in pure nickel. The strong positive
volume magnetostriction observed in the so-called
INVAR alloys is a band magnetism effect and will not
be discussed here (see Invar Materials: Phenomena).
In addition to the isotropic Heisenberg contribu-
tion, the exchange interaction also includes, in gen-
eral, anisotropic terms of increasing order which
depend both on the distance between interacting
spins and on the orientation of the bond with respect
to spin direction. The orientation dependence is the
origin of the magnetic anisotropy energy. Both the
distance dependence and the orientation dependence
are the origin of Joule magnetostriction.
6.2 Crystal Field Interaction
Ions with a nonspherical electron distribution inter-
act with the nonuniform electric field produced by
their neighbors—the so-called crystal field. This in-
teraction can be expanded in terms of orbital mul-
tipolar moments and associated field spatial
derivatives. For example, the lowest moment is quad-
rupolar and it is coupled to the first field derivatives
(the field gradient tensor). In any case this electro-
static energy depends on the orientation of the elec-
tron orbitals with respect to the crystal field and
hence the crystal axes (see Localized 4f and 5f Mo-
ments: Magnetism). In magnetic ions the magnetic
moment is either tied to the orbitals or coupled to
them by spin–orbit interaction. The final result is that
there is a contribution to the free energy of the crystal
that depends on the orientation of the spontaneous
magnetization with respect to the crystal axes, i.e., an
anisotropy energy. The dependence of this anisotropy
energy on (anisotropic) strain leads to the Joule mag-
netostriction. It must be emphasized here that high
magnetostriction does not necessarily imply large an-
isotropy since a function may be zero at a given value
of the variable while its derivative is not.
7. Practical Magnetostrictive Mater ials and their
Applications
From a practical point of view it is worth distin-
guishing four main families of magnetostrictive ma-
terials: (i) the so-called INVAR alloys; (ii) the high
coupling factor alloys; (iii) the high-saturation mag-
netostriction alloys; and, finally (iv) the ferrite crys-
tals or ceramics which, in contrast to the previous
metallic materials, are almost perfect insulators.
7.1 INVAR Alloys
It was discovered by Guillaume in 1896 that in some
alloys of nickel and iron the volume magnetostriction
is positive and its temperature dependence just com-
pensates for the normal thermal expansion of the
alloy. The result is a metallic alloy bearing a very
weak thermal expansion coefficient over a wide
temperature range. The applications of these INVAR
alloys include very large structures such as methane
tankers as well as the most tiny parts of metrology,
together with very specific electronic components,
such as the masks for high-resolution color TV
(du Tremolet de Lacheisserie 1993). A drawback of
these materials is that they exhibit a very large forced
volume magnetostriction, dV/VdHD10
10
mA
1
,
preventing their use in a high magnetic field envi-
ronment.
7.2 High Coupling Factor Alloys
This category includes magnetically soft polycrystal-
line and amorphous alloys based on iron, nickel, and
cobalt. Their saturation magnetostriction is rather
low (l
s
o50 10
6
) and their high coupling factor is
rather a consequence of their very low anisotropy.
The most remarkable and useful example of this
category of materials is an amorphous alloy known
as Metglass 2605 SC with the composition Fe
81
B
13.5
Si
3.5
C
2
. Due to its fabrication technique (Kavesh
1977), this alloy is available only in the form of a thin
ribbon (around 25 mm thick). Table 1 lists some of its
relevant characteristics. The last four parameters may
be considered as ‘‘soft’’ since they depend strongly on
postdeposition treatments which modify all the prop-
erties that are related to anisotropy. It is well known
that intrinsic anisotropy in amorphous materials is
actually a random function of the spatial position
with a correlation length typically less than 1 mm.
Extrinsic large-scale anisotropy can, however, be in-
duced by appropriate treatments.
Typically, annealing at 642 K for 10 min under a
saturating magnetic field parallel to the ribbon plane
840
Magnetostrictive Materials
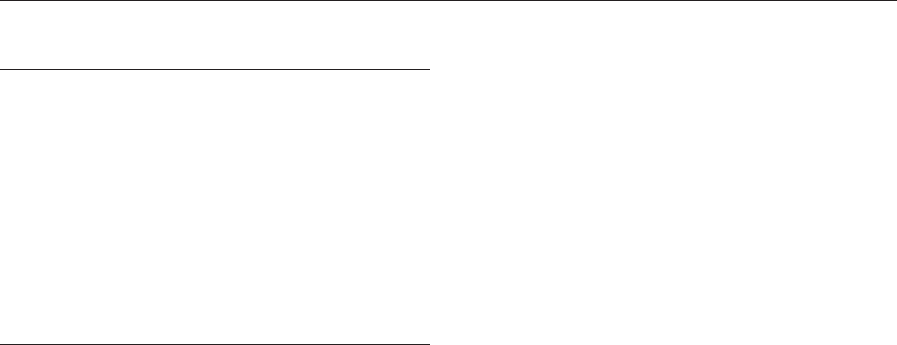
induces a uniaxial anisotropy with an easy axis par-
allel to the applied field. The value of the induced
anisotropy field is in the order of 50A m
1
. Such a
field-annealed Metglass ribbon has uniaxial symme-
try and, as explained in Sect. 5, it may be character-
ized by differential piezomagnetic parameters around
a given bias point. It is usual to take the easy axis as
the z or ‘‘3’’ axis. Table 1 refers to a field-annealed
Metglass alloy in the demagnetized state under zero
field and zero stress, unless otherwise specified.
Remarkable points in Table 1 are: (i) an extremely
high coupling factor, (ii) a giant DE effect (from
25 GPa at zero field up to 200 GPa at high bias field,
i.e., at blocked magnetization); and (iii) an extreme
sensitivity of permeability to applied stress. However,
this is associated with a rather low saturation mag-
netostriction. All these characteristics make the Met-
glass alloy a very good candidate for low-power
transducer applications (du Tremolet de Lacheisserie
1993, du Tremolet de Lacheisserie et al. 1998).
Force transducers make use of the stress depend-
ence of permeability, and more generally of the modi-
fication of magnetic response by stress. A significant
advantage of these transducers is that since magnetic
measurements do not require physical contact with
the material, it is quite easy to sense forces acting on
moving parts. As an example, consider the noncon-
tact measurements of the torque transmitted by a
rotating shaft. A Metglass ribbon is wrapped around
the shaft and is submitted to the shearing forces as-
sociated with the torque. The ribbon permeability is
measured by a fixed coil arrangement placed close to
the moving ribbon surface. Permeability must be
measured along one of the principal stress directions,
in this case at 451 off the shaft axis.
7.3 High-saturation Magnetostriction Alloys
Giant magnetostrictive effects were discovered in
1975 in the intermetallic cubic compound TbFe
2
,
known as Terfenol (Clark 1980). This alloy exhibits
magnetostrictive deformations which are 50 to 100
times larger than the high coupling factor materials.
Such a giant magnetostrictive effect can be clearly
explained by the localized electron model as a crystal
field effect on the rare-earth site. Unfortunately this is
obtained at the price of a relatively large anisotropy.
Therefore, high driving fields are necessary to gener-
ate the magnetostrictive deformation.
The improved alloy Tb
0.3
Dy
0.7
Fe
2
, known as Ter-
fenol D, still has a very large magnetostriction but a
much lower anisotropy. This is because the main
contributions to anisotropy, due to terbium and dys-
prosium, have opposite signs and nearly compensate
for each other at this composition, whereas the re-
spective contributions to magnetostriction do not.
Table 2 lists some useful room-temperature charac-
teristics of Terfenol and Terfenol D. Even the im-
proved material remains relatively hard and despite
the very large saturation magnetostriction, the mag-
netomechanical coupling factors are definitely lower
than those of low-saturation magnetostriction but
very soft alloys.
Progress in giant magnetostriction materials has
been directed towards the fabrication of highly tex-
tured materials and even single crystals (Clark 1986).
Potential applications of giant magnetostriction
alloys include large displacement transducers and
high-power ultrasonic generation. However for static
displacement generation, piezoelectric transducers
based on PZT ceramics are still the best choice main-
ly because they do not require a permanent excitation
power.
In contrast, Terfenol D is a better candidate than
PZT for high-power ultrasonic generation (Claeyssen
et al. 1988) because it is not brittle and it generates a
higher deformation and higher power density. A no-
ticeable disadvantage of these alloys is their metallic
electrical conductivity which, due to the so-called
skin effect, prevents their use at high frequency.
Giant magnetostriction alloys were also prepared
as thin films, with the idea that new specific routes to
a vanishing anisotropy could be followed in view of
applications to low driving field microactuators (du
Tremolet de Lacheisserie et al. 1998). Thin films of
amorphous Tb
1–x
Dy
x
(Co
0.55
Fe
0.45
)
y
were deposited
by Duc et al. (1996) using d.c. sputtering. Due to their
amorphous structure these films are expected to have
a vanishing large-scale magnetic anisotropy together
with an isotropic, and still giant, magnetostriction. In
practice they always bear some induced anisotropy of
various origins. It is preferable in most cases inten-
tionally to induce a homogeneous in-plane uniaxial
anisotropy rather than to rely on uncontrolled (and
often spatially inhomogeneous) parasitic effects.
This is done both by controlling the sputtering
conditions (Quandt et al. 1994) and by applying a
bias field, either during the deposition itself or during
a postdeposition treatment (typically 10 min to 1
Table 1
Some relevant characteristics of Metglass 2605SC.
Young’s modulus at blocked magnetization
Y
M
33
(GPa) 200
Curie temperature (K) 643
Spontaneous induction at 300 K (T) 1.61
Saturation magnetostriction at 300 K, 10
6
30
Relative permeability, m
33
20000
Relative permeability m
33
under stress bias
(T
33
¼1 MPa) 80000
Static magnetostrictivity d
33
(nm A
1
) 1000
Magnetomechanical coupling factor k
33
(under 50A m
1
bias field) 0.97
Young’s modulus at free magnetization Y
H
33
(GPa) 25
841
Magnetostrictive Materials

hour at 150–300 1C under a 10000 A m
1
field). Films
are deposited on substrate plates (silicon or pyrex) of
known elastic properties thereby constituting a mag-
netoelastic bimorph (Klokholm 1976). If the magne-
tostrictive layer is much thinner than the substrate
plate, the magnetostrictive stress at zero deformation,
rather than the magnetostrictive deformation at zero
stress, can be directly determined (du Tremolet de
Lacheisserie and Peuzin 1994). This is done by meas-
uring the curvature and torsion of the magnetoelastic
bimorph induced by a known applied field. Magne-
tostrictive deformation at zero stress can then be cal-
culated by making reasonable estimations of the layer
elastic modulus.
For example, in Tb
0.32
(Fe
0.45
Co
0.55
)
0.68
, a fairly
well-defined easy axis can be induced by an annealing
at 250 1C. The elongation, l(H), produced along the
in-plane hard direction is then determined as a func-
tion of the field H applied along the same direction.
Giant magnetostriction is observed with l(H) ¼
0.8 10
3
at m
0
H ¼0.3 T and still l(H) ¼0.3 10
3
at m
0
H ¼0.1 T. However, these driving fields are still
high for microsystem applications. This is due in part
to the ferrimagnetic character of these alloys which
leads to a rather low spontaneous magnetization
(m
0
M
s
D0.3 T) and therefore to a high anisotropy
field.
In order to improve further the low field magneto-
strictive response, a periodic laminar nanocomposite
was fabricated by repeated stacking of a weakly mag-
netostrictive, but high magnetization, layer of poly-
crystalline FeCo and a highly magnetostrictive
amorphous TbCo layer (Betz 1997). Typical layer
thicknesses were about 6 nm and up to hundreds of
layers could be stacked by using sequential sputter
deposition. As a consequence of the strong exchange
coupling between the FeCo and TbCo layers the ob-
tained films behaved as a homogeneous ferromagnetic
alloy combining relatively high magnetization and
giant magnetostriction. Deformation of up to 0.4
10
3
was obtained in a field of only 20 mT. These thin
films of giant magnetostriction alloys have given rise
to the development of various types of micromechan-
ical devices (du Tremolet de Lacheisserie et al.1998)
among which are a micropump (Quandt 1997), a tor-
sional microactuator which is claimed to be free of
thermal drift (Betz et al. 1996) and a two-dimensional
optical microscanner (Garnier et al. 1999). These de-
vices are, however, still at the laboratory level.
7.4 Magnetostrictive Insulators: Ferrites
Two families of magnetoelastic ferrites are worth
mentioning from the practical point of view: the
spinel ferrites of general formula MFe
2
O
4
where M is
a metal of the first transition series; and the garnets of
general formula R
3
Fe
5
O
12
where R is a rare-earth
metal or yttrium.
Magnetoelastic spinel ferrites such as NiFe
2
O
4
and
Ni
0.98
Co
0.02
Fe
2
O
4
have a resistivity in excess of
10
4
O.m, a spontaneous induction of 0.33 T, and a
Curie temperature of 863 K. Their spontaneous mag-
netostriction is comparable with that of high coupling
factor materials but since they are somewhat less soft,
their magnetomechanical coupling factors are modest
(0.2–0.38). These materials face a difficult competi-
tion with piezoelectric ceramics.
The garnets, especially Y
3
Fe
5
O
12
(YIG), have
found many applications in general microwave
devices, mostly because they are almost perfect insu-
lators and bear remarkable magnetodynamic prop-
erties (von Aulock 1965). Because of their excellent
acoustic properties, and despite their rather weak
magnetostriction (l
100
and l
111
are in the order of
10
6
), YIG single crystals have been exploited, at
least at the laboratory level, in magnetoelastic signal
processing devices taking advantage of such effects as
magnetic field control of acoustic propagation and
coupling between magnetostatic waves and acoustic
waves (Auld 1968, 1971).
See also: Magnetoelastic Phenomena; Magnetoelas-
ticity in Nanoscale Heterogenous Materials; Stress
Coupled Phenomena: Magnetostriction
Bibliography
Auld B A 1968 Nonlinear Interaction of Spin Waves and Elastic
Waves: Advances in Microwaves. Academic Press, New York
Auld B A 1971 Magnetostatic and magnetoelastic wave prop-
agation in solids. Appl. Solid State Sci. 2, 1–106
Betz J 1997 Magnetostriction ge
´
ante de couches minces et
microactionneurs magne
´
tostrictifs pour des technologies
inte
´
gre
´
es. Thesis, University of Grenoble, France
Table 2
Main characteristics of Terfenol (TbFe
2
) and Terfenol D (Tb
0.3
Dy
0.7
Fe
2
). Curie temperature T
c
, spontaneous
induction m
0
M
s
, saturation magnetostriction l
s
, magnetomechanical coupling factor k
33
, and static magnetostrictivity
d
33
.
Material T
c
(K) m
0
M
s
(T) 10
6
l
s
k
33
max d
33
max(nm A
1
)
TbFe
2
698 1.1 1750 0.35
Tb
0.3
Dy
0.7
Fe
2
653 1.0 1100 0.6 57
842
Magnetostrictive Materials

Betz J, Mackay K, Peuzin J, Halstrup B, Lhermet N 1996
Torsion based, drift free magnetostrictive microactuator. In:
Proc. Actuator ’96. Axon Technology Consult GmbH,
Bremen, Germany, pp. 283–6
Claeyssen F, Boucher D, Pohlenz C 1988 Application of mag-
netostrictive rare earth iron alloys to sonar transducers. In:
Proc. Undersea Defence Technology ’88. Microwave Exh. and
Pub. Ltd. Ed, London, 711pp
Clark A E 1980 Magnetostrictive rare earth—Fe
2
compounds.
In: Wohlfarth E P (ed.) Ferromagnetic Materials. North
Holland, Amsterdam
Clark A E 1986 Magnetostriction in twinned [112] crystals of
Tb
0.27
Dy
0
.
73
Fe
2
. IEEE Trans. Magn MAG-22, 973–5
du Tremolet de Lacheisserie E 1993 Magnetostriction. Theory
and Applications of Magnetoelasticity. CRC Press, Boca
Raton, FL
du Tremolet de Lacheisserie E, Mackay K, Betz J, Peuzin J C
1998 From bulk to film magnetostrictive actuators. J. Alloy.
Comp. 685–91
du Tremolet de Lacheisserie E, Peuzin J C 1994 Magnetostric-
tion and internal stresses in thin films: the cantilever method
revisited. J. Magn. Magn. Mater. 136, 189–96
Duc N H, Mackay K, Betz J, Givord D 1996 Giant magne-
tostriction in amorphous (Tb
x
Dy
1–x
)(Fe
0.45
Co
0.55
)
y
films.
J. Appl. Phys. 79, 973–7
Garnier A, Bourouina T, Fujita H, Hiramoto T, Orsier E,
Peuzin J C 1999 Magnetic actuation of bending and torsional
vibrations for 2D-optical-scanner application. In: Proc. 10th
Int. Conf. on Solid State Sensors and Actuators. Sendai, Japan
Kavesh S 1977 In: Leany H S, Gilman J J (eds.) Metallic glass-
es. American Society of Metals, Metals Park, OH
Klokholm E 1976 The measurement of magnetostriction in
ferromagnetic thin films. IEEE Trans. Magn. 12, 819–21
Nye J F 1957 Physical Properties of Crystals. Clarendon Press,
Oxford
Quandt E 1997 Giant magnetostrictive thin film materials and
applications. J. Alloy. Comp. 258, 126–32
Quandt E, Gerlach B, Seemann K 1994 Preparation and ap-
plications of magnetostrictive thin films. J. Appl. Phys. 76,
7000–2
von Aulock W 1965 Handbook of Microwave Ferrite Materials.
Academic Press, New York
J. C. Peuzin
Laboratoire Louis Ne
´
el, CNRS Grenoble, France
Magnets, Soft and Hard: Magnetic
Domains
Below the Curie temperature, the elementary mag-
netic moments of ferro- and ferrimagnetic materials
are spontaneously ordered (see Magnetism in Solids:
General Introduction). On a mesoscopic scale in the
nanometer range, many of these elementary dipoles
can be collected in an average value called magnet-
ization, which is represented by a classical vector
M(r) of unit A/m (r is the position vector). The ab-
solute value of the magnetization vector, given by the
saturation magnetization M
s
, is a function of tem-
perature alone for all regular magnetic materials, it is
constant throughout a (chemically uniform) sample
and is largely independent of applied magnetic fields.
We can therefore write M(r) ¼M
s
m(r) with m
2
¼1,
where m(r) is the unit vector field of magnetization.
For samples of finite dimensions, this vector field is
usually subdivided into magnetic domains, i.e., vol-
umes that are themselves uniformly magnetized to a
value equal to M
s
along different directions. They are
separated by domain walls, in which the magnetiza-
tion vector continuously rotates on the 10–1000 nm
scale to accommodate the change in magnetization
orientation between adjacent domains. Domain for-
mation is driven by energy minimization, with the
reduction of the stray field energy being responsible
for their development above all. The character of a
domain pattern depends on the strength and orien-
tation of ‘‘easy axes of magnetization’’ (anisotropy,
see also Magnetic Anisotropy) relative to the main
surfaces of the magnet, but also its shape, dimen-
sions, and physical microstructure are important.
The magnetic microstructure, i.e., the arrangement
of domains and walls, together with their reaction in
external magnetic fields (magnetization processes)
determine the macroscopic properties of magnetic
materials. Due to the presence of domains, a magnet
can accommodate a continuous range of magnetic
states that reach from complete demagnetization (if
the moments of all domains cancel each other) to
saturation in external fields. In soft magnetic materi-
als, the magnetic microstructure can easily be mod-
ified in small fields either by wall motion or
magnetization rotation.
For instance, a high permeability in the core of
inductive devices is provided by easily displaceable
domain walls leading to a steep magnetization curve,
whereas a linear curve for sensor applications re-
quires rotation processes mainly. If major and irre-
versible rearrangements of domains occur during
magnetization, they are responsible for losses and
noise in devices, and pinning of domain walls by
material imperfections results in hysteresis with co-
ercivity and remanence (see Magnetic Hysteresis).
Strong pinning or the prevention of domain nuclea-
tion causes a high coercivity and leads to hard mag-
netic materials (see Hard Magnetic Materials, Basic
Principles of ).
In Sects. 2 and 3 of this contribution, the basic
domain structures in both material classes will be re-
viewed based on Kerr-microscopical domain studies
(see Kerr Microscopy ), following some introductory
remarks on the fundamentals of domains in Sect. 1.
Reviews on magnetic materials with emphasis on
magnetic microstructure can be found in Cullity
(1972), Chikazumi (1997), and O’Handley (2000). A
comprehensive review on domains together with an
extended bibliography is given in Hubert and Scha
¨
fer
(1998).
843
Magnets, Soft and Hard: Magnetic Domains
1. Fundamentals of Magnetic Domains
1.1 Energetics of a Ferromagnet
Domain formation is driven by minimization of the
total free energy. The relevant magnetic energies are
introduced here by showing their effect on the mag-
netization vector field of (soft) magnetic films (Fig. 1).
(a) Exchange energy
A ferromagnet prefers a parallel alignment of mag-
netization vectors (Fig. 1(a)). Deviations from this
condition invoke an energy penalty, the exchange
energy that can be described by a stiffness expression
E
ex
¼A
R
(grad m)
2
dV (A is the exchange constant).
(b) Stray field energy
A saturated state as assumed in Fig. 1(a) would cause
a magnetic stray field for a finite sample. This can be
derived from the material law B ¼m
o
(H þM) and
Maxwell’s equation div B ¼0(B is the magnetic flux
density in teslas and H the magnetic field in amperes
per meter), leading to div H ¼div M. The sinks and
sources of magnetization (div M) may be interpreted
as magnetic charges (note that magnetic charges never
appear isolated but are always balanced by opposite
charges, different to electric charges). A field arises
from these charges that acts as stray field outside the
sample and as demagnetization field in the interior.
Volume, interface, and surface charges may be dis-
tinguished (Fig. 1(b)), the latter occurring if the
magnetization vector is not parallel to a surface or
edge. The energy connected to the stray field is
E
stray
¼0.5 m
o
R
H
stray
MdV. It scales with the factor
K
d
¼M
2
s
m
o
/2 (stray field energy coefficient, units J
m
3
), which is a measure of the maximum stray field
energy density of a material.
If the stray field energy dominates, flux-closed
magnetization configurations will develop that tend
to avoid stray fields. For the disk in Fig. 1(a), a con-
centric pattern would be completely charge-free, at
the expense of some exchange energy though. Such a
continuously flowing, isotropic configuration is in
fact observed in anisotropy-free NiFe (Permalloy)
disks (Fig. 1(c)).
The existence of ‘‘real’’ domains is, in a con-
ventional picture, connected with the presence of
anisotropy, which would favor homogeneously mag-
netized volumes along ‘‘easy directions.’’ However,
in thin film elements, domains can also be present in
the absence of anisotropy, just induced by the shape
as shown in Fig. 1(d) for rectangular and elliptical
elements. This follows from the requirement of pole
avoidance (Van den Berg 1986): To be completely
stray-field-free, the vector field m must be diver-
gence-free within the element (div m ¼0), it must
be parallel to the edges and to the film plane, and
it must have a constant length (7m7 ¼1). These
Figure 1
The effect of magnetic energies on domain formation,
demonstrated for magnetic films. The magnetic charges
(b) of the hypothetical, saturated state in (a) can be
avoided by a flux-closed configuration as observed by
Kerr microscopy on a Fe
81
Ni
19
(Permalloy) film disk of
240 nm thickness (c). The shape-induced domains of the
anisotropy-free Permalloy elements in (d) are modified
by magnetization-induced anisotropies of the order of
100 J/m
3
in (e). The stress-induced anisotropy of the
extended amorphous CoFeSiMo-film (f) (thickness
800 nm) is an order of magnitude higher than that of
Permalloy, leading to a spike-like closure structure at the
film edge. In the (100)-oriented, single-crystalline iron
film of 100 nm thickness (g), four domain ‘‘phases’’ are
found according to crystal anisotropy. External
magnetic fields can cause wall motion and magnetization
rotation as shown for 240 nm-thick NiFe elements in
(h) and (i), respectively.
844
Magnets, Soft and Hard: Magnetic Domains

requirements can only be met simultaneously if
the magnetization stays parallel to the edges on
every point along an edge normal, as long as no
other edge interferes. Consequently, uniformly mag-
netized domains result in a certain neighborhood
of straight edges. Similar considerations also apply
to bulk specimens. However, in most magnetic
specimens (especially in bulk magnets) the occur-
rence of ‘‘regular’’ domains and their arrangement
is, in fact, strongly connected with the presence of
anisotropy.
(c) Anisotropy energy
In most magnetic materials, easy axes do exist that
are preferably occupied by the magnetization vector.
Deviations cause an anisotropy energy E
anis
¼
K
u
sin
2
y (for a uniaxial anisotropy, where y is the an-
gle between easy axis and magnetization, and K
u
is
the anisotropy constant in J m
3
) (see also Magnetic
Anisotropy).
Anisotropy may have different origins. In the case
of Permalloy films, for example, a uniaxial anisotropy
may be caused by preferred pair ordering of the
atomic nickel and iron components along the local
magnetization direction present during film deposi-
tion or at annealing (magnetization-induced anisot-
ropy). Well-defined easy axes can be induced by
annealing in magnetic fields, leading to oriented basic
domains and closure domains at the sample edges to
avoid magnetic charges (Fig. 1(e)). The anisotropy
energy of the hard-axis closure domains could be re-
duced by decreasing their volume. This, however,
necessarily would decrease the basic domain width at
the expense of domain wall energy. The wall energy is
proportional to O(AK) because in a wall, the mag-
netization deviates from the anisotropy axes and
from parallel arrangement. So the domain structures
in the case of Fig. 1(e) are determined by the min-
imization of anisotropy and wall energy under the
constraint of zero stray field energy.
Mechanical stress may induce or modify anisotro-
pies as well, if the magnetostriction constant is dif-
ferent from zero. The stress-induced anisotropy in the
amorphous film of Fig. 1(f) is an order of magnitude
larger than the magnetization-induced anisotropy of
the Permalloy elements in Fig. 1(e). Towards the film
edge, the stray field energy is reduced by domain re-
finement in a spike-like way rather than by closure
domains, which would involve considerable aniso-
tropy energy. This mechanism of magnetostatic en-
ergy reduction by subdivision of the pole distribution
towards an edge or surface is generally found in high-
anisotropy, uniaxial materials.
In crystalline materials, the magnetocrystalline an-
isotropy—the preference of the magnetization vector
to align with so-called easy crystal axes—is usually
dominating. In the example of Fig. 1(g), two of the
/100S easy axes in a single crystalline iron film are
occupied, leading to a four-phase domain pattern
with charge-free 1801 and 901 domain walls.
Another important phenomenon can be seen in
Fig. 1(g): the edge of the extended film is misoriented,
i.e., it does not contain an easy axis. Here the two
requirements of using only easy directions and avoid-
ing stray fields are incompatible. A compromise is
found by domain branching: towards the film edge, the
pattern is refined in several generations of easy-axis-
domains, so that the hard-axis closure domains
(necessary to completely avoid stray fields) are get-
ting as small as possible. They are restricted to the
outermost edge and are not resolved in the image. Far
away from the edge, the domains stay wide to save
wall energy. The branching process connects the wide
and narrow domains in a way that depends on the
number of easy directions. In Fig. 1(f), for instance,
only two-phase branching is possible due to the uni-
axial anisotropy. In the case of a very weak uniaxial
anisotropy (Fig. 1(e)), regular closure domains rather
than branching may be preferred on misoriented
edges. Domain branching also plays a major role in
bulk materials if the easy directions are incompatible
with the surface orientation. For strongly misoriented
surfaces, a low energy is achieved by simple domains
in the volume and a finely divided surface pattern.
(d) Magnetostrictive energy
A magnetic material with a nonvanishing magneto-
striction constant is elongated along the magnetiza-
tion direction. If the spontaneous deformations of the
various parts of a domain pattern do not fit together
elastically, a magnetostrictive self-energy arises that
can modify the domain arrangement, especially in
bulk materials.
(e) Zeeman energy
Applying an external field also adds energy. Domains
with magnetization components along the field di-
rection are favored and grow by wall displacement
(Fig. 1(h)). In stronger fields, magnetization rotation
occurs (Fig. 1(i)).
1.2 Classification of Materials and Domains
The character of a domain pattern is determined by
the relative size of anisotropy and stray field energy,
defined by the dimensionless material parameter
Q ¼K/ K
d
(where K
d
¼M
2
s
m
o
/2 is the stray field ener-
gy coefficient, and K is the effective anisotropy con-
stant). If the stray field energy dominates (Q51),
then flux-closed domain patterns develop that avoid
stray fields, eventually at the expense of anisotropy
energy in closure domains at surfaces if they do not
contain an easy axis. A dominating anisotropy energy
(Qb1) forces the magnetization along easy axes, al-
lowing for magnetic charges.
845
Magnets, Soft and Hard: Magnetic Domains
The ratio Q determines the applicability of a ma-
terial. A soft magnetic material should have a small
value Q51, and strong permanent magnets are often
based on materials with Qb1. Note, however, that
the properties of high and low relative anisotropy are
not directly related to magnetic hardness, i.e., to high
and low coercivity. Coercivity, as an extrinsic prop-
erty, depends on additional structural features such
as defects, grain boundaries, sample or particle size,
and surface irregularities in conjunction with the
magnetic microstructure. The intrinsic Q-parameter
determines the potential to achieve a desired mag-
netic hardness (or softness).
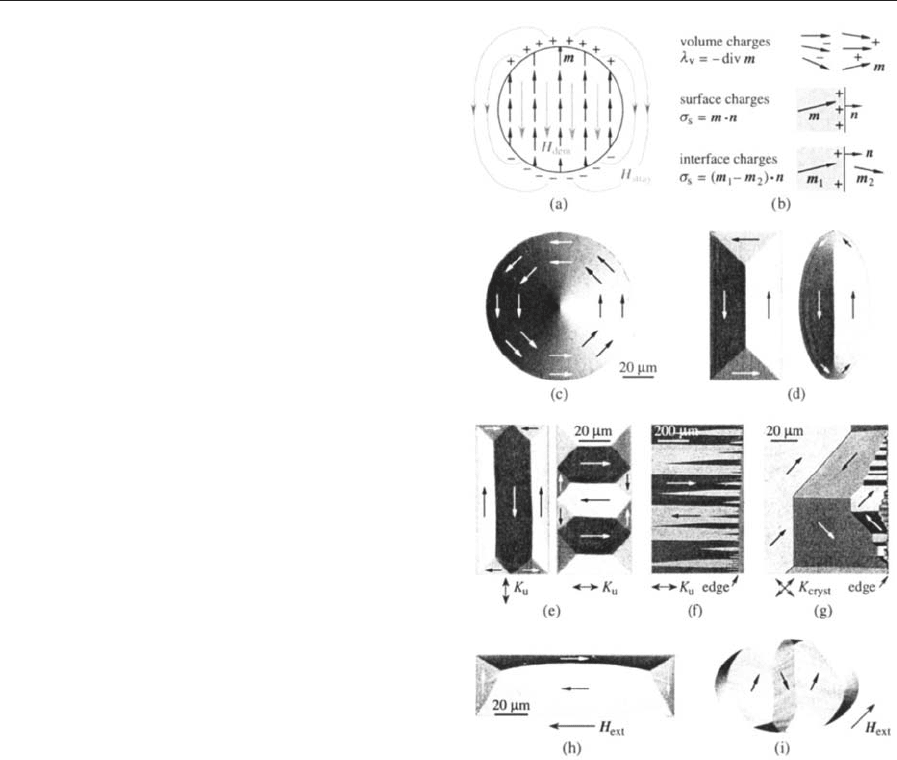
1.3 Domain Walls
The characteristic feature of thin soft magnetic films
(thinner than 30 nm for Permalloy) is the symmetric
Ne
´
el wall with an in-plane magnetization rotation
(Fig. 2(a)). This is a magnetically charged wall, where
most of the charges are concentrated in a wall core
which scales with the exchange length of the stray-
field energy O(A/K
d
)(¼5 nm for Permalloy). In thick
films (thicker than 100 nm for Permalloy), the
charged walls are replaced by completely stray-field-
free, two-dimensional vortex walls (Fig. 2(b)). The
width of the vortex scales with the film thickness.
Above a thickness of the order of 5O(A/K) (where
K is crystal or an induced anisotropy), a wall struc-
ture develops, which is still related to the asymmetric
Bloch wall of thick films. Instead of a single vortex in
the middle, two vortices are formed in the neighbor-
hood of the surfaces that close most of the magnetic
flux arising from the polar magnetization compo-
nents in the wall interior (Fig. 2(d)). In the volume,
this stray-field-free wall assumes a one-dimensional
character with a rotation parallel to the wall plane as
in a classical Bloch wall (see Fig. 2(c)), and at the
surfaces, the magnetization rotates in-plane. Whereas
the surface wall width steadily increases with thick-
ness, the interior wall width approaches the classical
value of pO(A/K). Note that even in low-Q materials
the wall width stays finite, because a real soft mag-
netic material is never completely anisotropy-free,
even if it has extremely high permeability. In high-Q
materials, the surface vortices are more or less sup-
pressed and the wall approaches the classical Bloch
wall structure (c) all through, allowing for magnetic
charges at the surfaces.
2. Domains in Soft Magnetic Materials
Soft magnetic materials play a major role as core
material in inductive devices. Such devices rely on
the high permeability of their cores that reaches val-
ues up to one million times the air value. Domain
wall displacement is the primary origin of this ex-
traordinary quality of soft magnetic materials. But
also, magnetization rotation can lead to high perme-
ability if anisotropies are uniform and small. De-
pending on applications, magnetization processes
have to be carefully controlled by selecting proper
materials with suitable domain patterns. In high-fre-
quency applications, for instance, wall displacement
processes are generally less favorable than rotation
Figure 2
The fundamental types of domain walls in soft magnetic
materials. In a, b, and d, the surface magnetization and
the projection on the cross-section plane is schematically
shown together with observations by Kerr microscopy.
The black-and-white wall segments are due to different
chiralities of the surface magnetization. The magnetic
charges of the Ne
´
el wall (a) are distributed between a
sharply localized core and extremely wide tails, which
take over a good part of the rotation. The asymmetric
Bloch wall (b) and its derivative for high sample
thickness (d) are free of magnetic charges. The slight
tilting of some wall segments in (d) is a consequence of
the vertical flux, indicating segments of opposite
chirality. Those transitions not connected with a kink
represent mere ‘‘cap switches’’—a change in the
orientation of the surface vortex without a change in the
basic wall chirality. The classical (symmetric) Bloch
wall, which is approached in high-Q materials, is
sketched in (c) for comparison. Here, the magnetization
rotates parallel to the wall plane across the whole sample
thickness.
846
Magnets, Soft and Hard: Magnetic Domains

because of the ‘‘anomalous’’ eddy current losses con-
nected with wall motion (see Magnetic Losses).
The avoidance of wall motion requires that all 1801
walls are oriented perpendicular to the field direction.
This can be achieved in ring cores of low-anisotropy
materials with a transverse easy axis, showing a linear
response with low remanence and coercivity. Irregu-
larities connected with domain wall pinning and do-
main annihilation or creation processes cause losses
in electrical machines and noise in communication
and sensor devices. A general rule is: if the character
of the magnetic microstructure can be improved in
the sense of a more regular domain structure leading
to more reversible magnetization processes, a better
performance of inductive devices can be achieved.
In this section, the magnetic microstructure of se-
lected soft materials is reviewed. Emphasis will be on
equilibrium domains in the field-free state, largely
neglecting the rich variety of patterns that occur on
application of magnetic fields. The domains in all soft
magnetic materials follow the principle of flux closure
(Q51), but anisotropy together with the surface ori-
entation has a decisive influence on domain arrange-
ment.
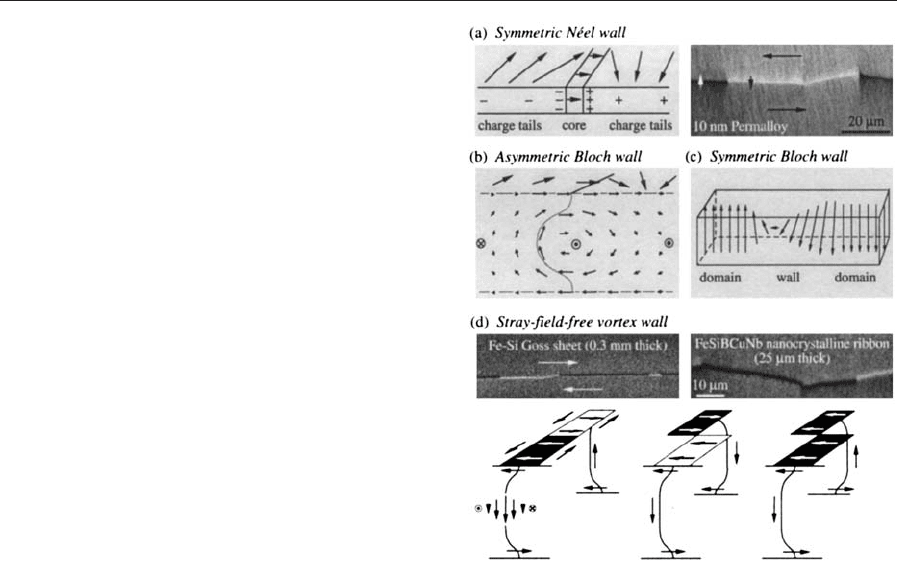
2.1 Grain-oriented Electrical Steel
Grain-oriented transformer material consists of large
grains of Fe 3 wt.% Si. They are oriented within a few
degrees deviation of the [001] easy direction from the
preferred axis of the material. The surfaces of all
grains are (110)-related within the same accuracy in
misorientation (forming altogether a [001](110) tex-
ture, the Goss texture). The sheets are insulated by
thin ceramic layers to avoid eddy currents between
the sheets and to provide favorable mechanical stress
(see also Steels, Silicon Iron-based: Magnetic Proper-
ties).
The basic domain structure of well-oriented Goss
grains consists of wide domains magnetized parallel
and antiparallel to the easy [001] direction (grain A in
Fig. 3(a)). If the [001] direction is slightly misoriented
out of plane (grains B, C), the basic domains are
supplemented to reduce the stray field energy: shal-
low surface domains (lancets) collect the perpendic-
ular flux, which would otherwise emerge from the
surface due to the misorientation, and feed it into
internal transverse easy-axis domains where it is
transported to the other surface of opposite charge
polarity or to the neighboring basic domain to be
distributed again (Fig. 3(d)). In a variant, the lancets
join into combs (grain C) by using a common internal
transverse domain that is properly oriented to avoid
magnetostrictive energy. Therefore, the combs are
aligned along a /111S-axis at the surface.
The magnetization process along the preferred
axis occurs by motion of the basic 1801 walls. How-
ever, during a magnetization cycle, the system of
supplementary domains is destroyed and rebuilt.
The energy bound in the supplementary domains is
lost in every cycle, thus forming an important part
of hysteresis loss in transformer sheets. Since sev-
eral nonplanar easy axes are always engaged in
Figure 3
(a) In Goss-textured transformer steel, simple (grain A)
or supplemented-bar domains (grains B, C) are
observed, depending on the misalignment of the [001]
easy axis relative to the surface (that is 01,11, and 21 in
grains A, B, C, respectively). Details of grain B are
shown at higher magnification in (c) together with a
three-dimensional model of a supplementary pattern in
(d). A uniaxial tensile stress along the preferred axis
(b) largely suppresses the supplementary domains and
causes domain refinement in misoriented grains, which
also extends to well-oriented grains to maintain flux
continuity. The tensile stress of 2 kg mm
2
in (b) was
applied externally to simulate the stress-effective
insulation coating that was removed here to allow for
Kerr microscopy. If the basic domains (e) of a stressed
grain are wiped out during the magnetization cycle, the
supplementary domains return (f). Images (e) and (f) are
from the same location, but a field is applied in (f)
leading to a relative magnetization of M/M
s
¼0.9.
847
Magnets, Soft and Hard: Magnetic Domains

supplementary domain patterns, their generation
and annihilation is also connected with magnetos-
trictive, acoustic noise (note that the magnetostrictive
elongation would not change by the motion of a
1801 wall).
Two possibilities do exist to avoid the unfavorable
supplementary domains. They can be largely sup-
pressed by mechanical tensile stress along the pre-
ferred axis (Fig. 3(b)). It magnetostrictively favors the
basic domains and wipes out the transversely mag-
netized domains. The basic domain spacing is then
decreased because otherwise the overall stray field
energy would rise in the absence of the supplementary
domains. The reduced domain width also reduces
anomalous eddy current losses, which become im-
portant if the basic domain width is larger than the
sheet thickness. Fortunately, the planar stress exerted
by the stress-effective insulating coating is for the
Goss texture equivalent to a uniaxial stress along the
preferred axis and will thus suppress supplementary
domains. Note, however, that for magnetostatic rea-
sons, the lancet structure reappears when the basic
domains are wiped out during the magnetization cy-
cle as is demonstrated in the sequence in Fig. 3(e) and
3(f). This causes extra losses.
It is also possible to avoid supplementary domains
completely if a misorientation of better than one de-
gree is achieved. But such a quasi-single-crystalline
material would tend to develop very wide basic do-
mains (Fig. 4(a)) with correspondingly large anom-
alous eddy current losses. The basic domain width
can be artificially reduced by scratching or by laser
scribing (Fig. 4(b)). The stress introduced locally in
this way interrupts the basic domains, acting like an
artificial grain boundary (see also Steels, Silicon Iron-
based: Magnetic Properties).
2.2 Nonoriented Electrical Steel
Figure 5 gives an impression of the huge variety of
domains on the surface of nonoriented silicon–iron
material commonly used in rotating electrical ma-
chines (see also Steels, Silicon Iron-based: Magnetic
Properties). Domain complexity depends on crystal
orientation. Domains in ideal Goss-grains (grain A)
or slightly misoriented Goss-grains (grain B) are
readily identified by comparison with Fig. 3. In the
(100)-oriented grain (C), a simple four-phase surface
pattern is found as in the corresponding thin film case
(Fig. 1(g)). Note, however, that for a thick sheet also
the easy axis perpendicular to the surface will be oc-
cupied by internal domains. A slightly misoriented
(100) surface (grain D) shows fir-tree domains—a
supplementary pattern that distributes the perpen-
dicular flux between neighboring basic domains by
shallow surface domains.
With stronger misorientation, the supplementary
domain system becomes increasingly complicated
(grain E in Fig. 5), and above a critical misorienta-
tion, branched domain patterns take over (grains F
and G in Fig. 5). Branching (see Sect. 1) at the surface
of a bulk cubic material occurs in a similar way as
shown in Fig. 1(g) for a two-dimensional case, but
further possibilities will be added by allowing the
third dimension to be used both by the magnetization
direction and by the spatial domain structure. The
fractal nature of branched patterns with up to four
generations of domains is also revealed in the surface
pattern of the extremely misoriented grain G (for this
(111)-surface the easy axes are aligned at the maxi-
mum angle of 541 relative to the surface). Note that in
a fine-grained material, not only the orientation of
the free surface is important. Even if there might be
grains for which this surface is well oriented, there
can be inner grain boundaries that are strongly mis-
oriented, consequently dominating the domain pat-
tern in the whole grain.
The bottom images in Fig. 5 give an impression of
the complicated domain reorganization processes in
misoriented grains when a magnetic field is applied.
Only the fact that the branched surface structures are
confined to a limited near-surface zone (of about
Figure 4
Domain spacing in well-oriented grains (a) can be
reduced by laser scribing (b). The stress between the
laser spots causes unfavorably oriented domains that
interrupt the basic domains (c). Image (b) was obtained
by applying a powder emulsion to a laser-treated surface
with insulating coating, whereas the Kerr image (a) is
from the same location after removing the coating and
relieving stress by annealing. Kerr image (c) was
obtained before annealing at higher magnification.
848
Magnets, Soft and Hard: Magnetic Domains
50 mm depth) makes a reasonable permeability in
nonoriented material conceivable, which will rely on
the underlying (wide) basic domains. The rearrange-
ment of the branched closure pattern causes a kind of
friction for the displacement of the basic domain
walls and leads to unavoidable hysteresis losses.
2.3 Crystalline High-permeability Materials
Much smaller anisotropies than in silicon–iron ma-
terial and thus higher permeabilities of more than
100 000 can be reached in NiFe alloys near the 80:20
composition, known as Permalloy or Mumetall.
These high-permeability materials are adjusted in
composition and heat treatment to reach zeros of
first-order anisotropy constant and in the mean mag-
netostriction constant. Nevertheless, regular domains
with clearly delineated domain walls are usually ob-
served within the crystallites of coarse-grained Perm-
alloy (Fig. 6(a)). They scale with the grain size and
change from grain to grain, demonstrating the influ-
ence of residual crystal anisotropy.
Figure 5
The domains on the surface of nonoriented electrical
steel (thickness 0.5 mm) depend on the orientation of the
crystallites. Patterns of selected grains are enlarged
below. The images in the bottom row show the same
location in a (111)-oriented grain, with a magnetic field
applied on the right.
Figure 6
In coarse-grained Permalloy sheets [(a), grain size
around 30 mm, thickness 20 mm], regular domains do
exist that are correlated over the grain boundaries.
Occasionally, domain walls may become dissolved in a
continuously rotating magnetization (c), if anisotropy
becomes negligibly small. In the fine-grained material
[(b), grain size around 13 mm], macroscopic domains
extend over many grains and are modulated by the local
anisotropies in the grains. A coarse-grained manganese–
zinc ferrite is shown in (d).
849
Magnets, Soft and Hard: Magnetic Domains
