Бунаков П.Ю., Рудин Ю.И., Стариков А.В. Основы автоматизированного проектирования изделий и технологических процессов

Подождите немного. Документ загружается.

Моделирование выбора технологий изготовления продукции,

обеспечивающих минимизацию затрат при выполнении заказа

Предположим, предприятие имеет разнообразное оборудование, отли-

чающееся технологией изготовления продукции. Необходимо выбрать такую

технологию, которая потребует от предприятия минимальных затрат при из-

готовлении заказанной продукции, а использованные ресурсы (материаль-

ные, трудовые и др.) не превысят имеющихся пределов. Для формализации

задачи вводятся следующие обозначения [15]:

i −

вид продукции;

l −

количество видов продукции;

j −

вид технологии изготовления продукции;

n −

количество видов технологий на предприятии;

x −

объем использованной j-й технологии за рассматриваемый

период производства заказанной продукции;

−

норма выпуска i-го вида продукции при использовании j-й

технологии при ее единичной интенсивности, т.е.

x =1;

−

объем заказа i-го вида продукции;

s −

вид ресурса;

k −

количество всех видов имеющихся ресурсов;

b −

норма использования s-го вида ресурса при использовании j-й

технологии с единичной интенсивностью;

c −

величина затрат (в денежном выражении) при использовании

j-й технологии с единичной интенсивностью.

Математическая модель данной (одноиндексной) задачи имеет сле-

дующий вид:

целевая функция, стремящаяся к минимуму

∑

→=

xcXW

min)(

с учетом ограничений на ресурсы

∑

≤

sjsj

bxb

, ( ks ,1= )

при выполнении объема заказа на производство изделий

∑

ijij

Qxa

, ( li ,1= ), где 0≥

x , ( nj ,1= ).

Рассматриваемая модель представляет задачу линейного программиро-

вания, для решения которой используется указанный выше симплекс-метод.

Компьютерный расчет модели может быть реализован с помощью процедуры

«Поиск решения», входящей в состав Microsoft Excel.

Модель максимизации объема комплектной продукции с учетом

возможностей технологического оборудования

Данная модель позволяет определить программу выпуска деталей стан-

ками (цехами) предприятия, при которой обеспечивается максимум выпуска

комплектной продукции (комплектов). Для формализации задачи вводятся

следующие обозначения [15]:

i −

номер вида деталей (комплектующих узлов), из которых

формируется комплектная продукция;

k −

количество видов деталей (комплектующих узлов);

r −

номер вида станка (цеха), на котором изготавливаются дета-

ли (комплектующие узлы) одного вида;

N −

количество единиц выпускаемой комплектной продукции

(количество комплектов);

R −

количество видов деталей (узлов);

b −

количество станков (цехов) r-го вида, т.е. изготавливающих

детали r-го вида;

l −

количество деталей i-го вида, необходимого для комплекто-

вания продукции;

a −

количество деталей i-го вида, которое может быть произве-

дено на одном станке (цехе) r-го вида за единицу времени;

x −

количество станков (цехов) r-го вида, предназначенные для

выпуска деталей i-го вида.

Математическая модель данной задачи имеет следующий вид:

max

→

, (6.7)

∑

≥

irir

Nxa

, ( ki ,1= ), (6.8)

∑

rir

, ( Rr ,1= ), (6.9)

≥

x , ( Rrki ,1;,1 == ), (6.10)

∈

. (6.11)

Пример 6.2. На предприятии имеются 5 типов станков (R=5), на которых должны

производиться 2 вида деталей (k=2), входящих в состав комплекта продукции, состоящей

из двух деталей первого вида (l

=2) и одной детали второго вида (l

=1). Количество стан-

ков первого вида b

=5, второго − b

=3, третьего − b

=40, четвертого − b

=9, пятого − b

=2.

Максимальные возможности производства деталей (узлов) на разных станках за один ме-

сяц приведены в табл. 6.2.

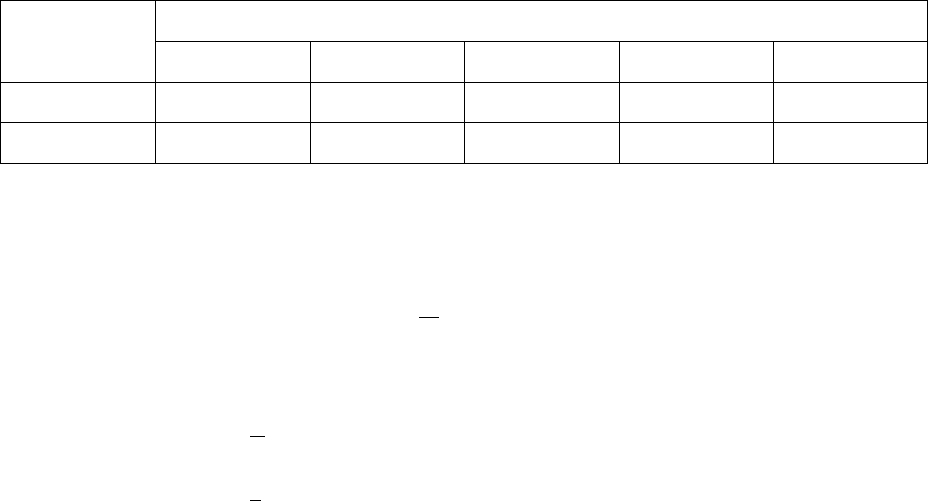
Таблица 6.2 Возможные объемы производства деталей (узлов)

различного вида на различных станках за один месяц

Вид станка (номер r) Вид детали

(номер i)

r=1 r=2 r=3 r=4 r=5

i=1 100 400 20 200 600

i=2 15 200 5 50 250

Составим математическую модель задачи. Используя формулы (6.7)−(6.10), можно

записать следующие соотношения:

целевая функция, стремящаяся к максимуму

max)( →= NXW ,

с учетом системы неравенств, представляющих условие комплектности продукции











≥++++

,)250502520015(

,)60020020400100(

2524232221

1514131211

Nxxxxx

системы уравнений, определяющих ограничения на количество имеющихся станков











,40

2515

2414

2313

2212

2111

и системы неравенств, описывающих тривиальные (естественные) ограничения

≥

x , ( 5,4,3,2,1;2,1

ri ).

Кроме того, при компьютерной реализации модели в Microsoft Excel

необходимо учесть условие ее целочисленности (соотношение 6.11).

Ниже представлена еще одна задача, относящаяся к моделированию

максимального объема выпуска изделий с учетом требования комплектности

конечной продукции. Дополнительным условием, усложняющим решение

задачи, является несбалансированность количества комплектующих узлов,

поступающих из различных источников [16].

Пример 6.3. Предприятие выпускает изделия, каждое из которых представляет со-

бой сборку из трех различных узлов, изготавливаемых на двух заводах. Из-за различий в

составе технологического оборудования производительность заводов по выпуску каждого

из трех видов узлов неодинакова. В табл. 6.3 содержатся исходные данные, характери-

зующие как производительность заводов по выпуску каждого из узлов, так и максималь-

ный суммарный ресурс времени, которым располагает каждый из заводов для производст-

ва этих узлов.

Таблица 6.3. Возможности заводов по выпуску комплектующих узлов

Производительность, узел/час

Завод

Максимальный не-

дельный фонд времени, час

Узел

1 100 8 5 10

2 80 6 12 4

Идеальной является такая ситуация, когда производственные мощности обоих за-

водов используются таким образом, что в итоге обеспечивается выпуск одинакового ко-

личества каждого из видов узлов. Однако этого трудно добиться из-за различий в произ-

водительности заводов. Более реальная цель состоит, по-видимому, в том, чтобы макси-

мизировать выпуск изделий, что по существу эквивалентно минимизации дисбаланса,

возникающего вследствие некомплектности поставки по одному или двум видам узлов.

Требуется определить еженедельные затраты времени (в часах) на производство

каждого из трех видов узлов на каждом заводе, обеспечивающие максимальный выпуск

изделий.

Составим математическую модель задачи. Возможный объем выпуска каждого из

трех видов узлов зависит от того, какой фонд времени выделяет каждый завод для их из-

готовления. Обозначим

x − недельный фонд времени (в часах), выделяемый на заводе

для производства узлов вида

. Тогда объемы производства каждого из трех комплек-

тующих узлов равны:

2111

68 xx + (узел 1),

2212

125 xx + (узел 2),

2313

410 xx + (узел 3).

Так как в конечном изделии каждый из комплектующих узлов представлен в одном эк-

земпляре, количество изделий должно быть равно количеству комплектующих узлов, объ-

ем производства которых минимален. Если, например, объем производства двух заводов

составляет 100, 112 и 108 соответствующих узлов, то количество конечных изделий будет

равно 100}108,112,100min{

. Поэтому количество конечных изделий можно выразить

через число комплектующих узлов следующим образом:

}410,125,68min{

231322122111

xxxxxx +++ .

Условия рассматриваемой задачи устанавливают ограничения только на фонд вре-

мени, которым располагает каждый завод. Таким образом, математическую модель можно

представить в следующем виде:

max}410,125,68min{)(

231322122111

→+++= xxxxxxXW

при ограничениях











==≥

≤++

).3,2,1;2,1(,0

100

232221

131211

jix

xxx

завод

(

),2

Данная модель не является линейной. Чтобы привести ее к линейной форме, следу-

ет выполнить следующее простое преобразование:

}.410,125,68min{

231322122111

xxxxxxy +++=

Тогда целевая функция запишется в виде

max)( →= yXW

при следующих ограничениях:











≥

≥+

,410

,125

,68

2313

2212

2111

yxx

Окончательно математическая модель задачи запишется в виде

max)( →= yXZ

при следующих ограничениях:











≥

==≥

≤++

≥−+

),3,2,1;2,1(,0

,80

,100

,0410

,0125

,068

232221

131211

2313

2212

2111

jix

xxx

yxx

Задача календарного планирования работы технологического

оборудования

Моделирование загрузки оборудования может быть рассмотрено с точ-

ки зрения отыскания оптимальной последовательности выполнения тех или

иных технологических операций. В деревообработке, например, в мебельном

производстве, это чаще всего относится к порядку запуска в обработку раз-

личных партий деталей. В лесопилении это связано с задачей определения

оптимальных размеров и порядку запуска в распиловку партий пиловочного

сырья с различными размерно-качественными характеристиками [17].

Задачи календарного планирования, рассматриваемые в рамках теории

расписаний, оказываются достаточно сложными с математической точки зре-

ния. Простейшей задачей календарного планирования является задача двух

станков, которая состоит в оптимизации порядка запуска в производство n

деталей, последовательно обрабатываемых на двух станках (операциях) при

условии, что в один и тот же момент времени на одном станке (операции) об-

рабатывается только одна деталь. Предполагается заданным продолжитель-

ность

t обработки i-й детали на j-ом станке, где i=1, 2, …, n; j=1, 2. Крите-

рием оптимальности является минимальная продолжительность выполнения

плана по обработке всех деталей на двух станках.

Решение этой задачи, полученное С. Джонсоном в 1953 году (по этой

причине ее часто называют задачей Джонсона), представляет собой простое

правило, указывающее порядок прохождения деталей по станкам в зависимо-

сти от времени их обработки на каждом станке [18].

Вначале все детали условно делят на две группы: в первую группу

включают те детали, для которых

21 ii

≤

(т.е. продолжительность обработки

на первом станке не превышает продолжительности обработки на втором

станке); во вторую − все остальные детали. В случае, когда минимальных

значений несколько, для определенности выбирают деталь с меньшим номе-

ром.

Затем детали первой группы упорядочивают (сортируют) по возраста-

нию продолжительности обработки, а детали второй группы − по убыванию,

и в таком порядке подают их для обработки на первом и на втором станках

соответственно.

Пример 6.4. Дан набор из пяти заготовок мебельных деталей, каждую из которых

следует обработать на двух станках: сначала на фрезерном станке (операция a), затем на

шлифовальном (операция b). Продолжительность (в мин.) обработки каждой заготовки на

станках приведена в табл. 6.4.

Таблица 6.4. Продолжительность обработки заготовок на станках

№ заготовки 1 2 3 4 5

1-й станок 6 4 14 2 14

2-й станок 12 2 8 4 6

Согласно описанному выше правилу (алгоритму) Джонсона, в первую группу сле-

дует включить заготовки с номерами 1 и 4, а во вторую − заготовки с номерами 2, 3, 5.

Очередность заготовок, после сортировки по продолжительности обработки, в пер-

вой группе − 4, 1, во второй − 3, 5, 2. Таким образом, оптимальный порядок обработки за-

готовок следующий: 4, 1, 3, 5, 2.

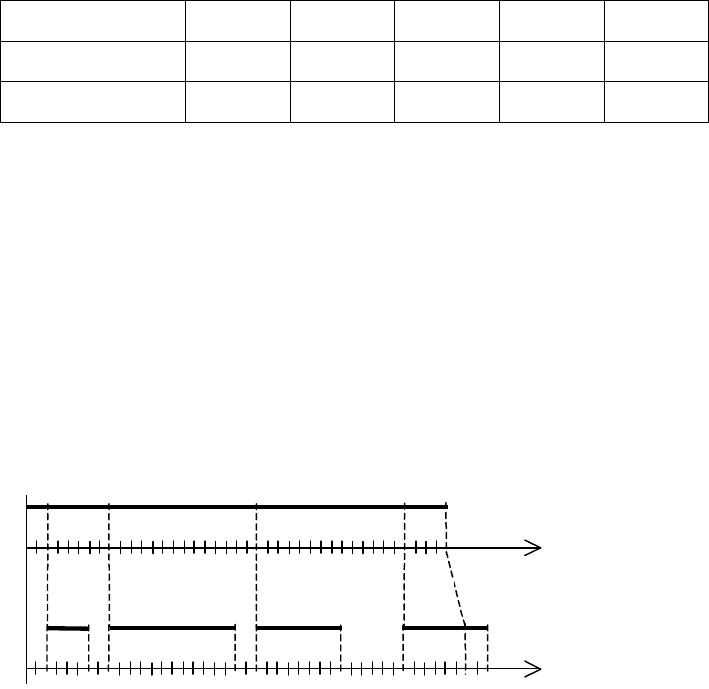
Продолжительность обработки на станках для найденной оптимальной последова-

тельности запуска заготовок может быть рассчитана с помощью диаграммы Ганта, пока-

занной на рис. 6.2. На ней каждому станку соответствует собственная ось времени t; на

осях отрезками прямых отмечены промежутки, в течение которых данный станок занят

обработкой той или иной детали.

й станок

Рис. 6.2. Диаграмма Ганта для задачи о двух станках

Как следует из диаграммы Ганта, суммарная продолжительность обработки загото-

вок пяти деталей на двух станках составляет 44 минуты. Первый станок не имеет просто-

ев, продолжительность его работы составляет 2+6+14+14+4=40 минут. Второй станок ра-

ботает 4+12+8+6+2=32 минуты, имея 12 минут простоя: по 2 минуты перед началом обра-

ботки заготовок 4-й, 1-й и 3-й деталей, 6 минут перед началом обработки заготовки 5-й

детали.

Для сравнения − общая продолжительность обработки деталей в соответствии с их

заданными порядковыми номерами составляет 46 минут, при этом время простоя второго

станка − 14 минут.

Следует отметить, что попытки получить аналогичным образом решения для трех

станков и более не увенчались успехом, за исключением отдельных частных случаев. При

переходе к общему случаю сложность задачи резко возрастает, что объясняется ее комби-

наторной природой, обуславливающей

m )!( вариантов, где m − число деталей, n − число

станков. При этом функция резко возрастает, так, например, 10!=3628800, а 11!=39916800.

Тем не менее, анализ алгоритма Джонсона позволил сформулировать ряд практиче-

ских рекомендаций (правил), которые можно распространить и на случай, когда число

станков превышает 2. В частности, при составлении расписания обработки деталей следу-

ет [17]:

1) обрабатывать раньше те детали, у которых время обработки на первом станке

минимально;

2) обрабатывать раньше те детали, у которых время обработки на последнем стан-

ке максимально;

3) обрабатывать раньше те детали, для которых «узкое место» (т.е. станок, на ко-

тором обработка данной детали занимает наибольшее время) находится дальше

от начала процесса обработки;

4) пропускать вперед детали, для которых общая продолжительность обработки на

всех станках максимальна.

Пример 6.5. В мебельном цехе деревообрабатывающего комбината изготавливают-

ся футляры для настенных и настольных часов, которые имеют следующие семь пронуме-

рованных деталей (m=7): 1 − вертикальный брусок двери; 2, 3 и 4 − нижний, средний и

верхний бруски дверки; 5 − нижняя доска; 6 − штанга; 7 − планка. Перечисленные детали

должны пройти последовательную обработку на следующих четырех (также пронумеро-

ванных) станках (n=4): 1 − рейсмусовом; 2 − фуговальном; 3 − торцовочном; 4 − фрезер-

ном. В табл. 6.5 приведена длительность обработки (в минутах) каждой детали на каждом

из станков.

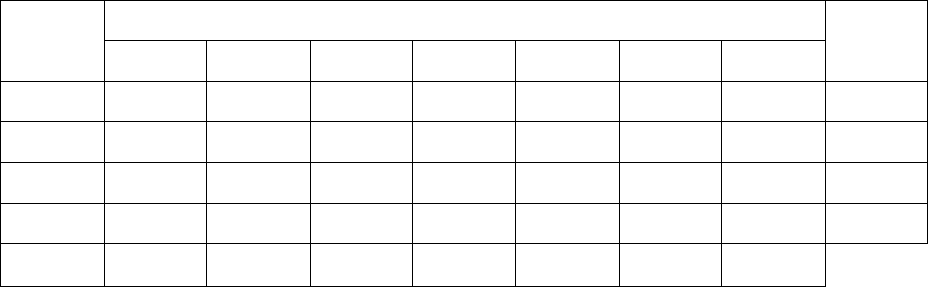
Таблица 6.5. Длительность обработки деталей на станках

Длительность обработки детали №, мин. №

станка

1 2 3 4 5 6 7

Σ, мин.

1 9 4 5 6 3 2 1 30

2 5 2 8 12 4 1 1 33

3 7 6 10 8 1 2 3 37

4 6 3 4 5 2 3 4 27

Σ, мин.

27 15 27 31 10 8 9

В соответствии с рассмотренными выше правилами можно рекомендовать сле-

дующие варианты запуска деталей в обработку (табл. 6.6). В случае, когда рассматривае-

мое правило не позволяет определить очередность обработки каких-либо двух деталей,

требуется обращение к одному из предыдущих правил.

Для определения общей длительности обработки деталей для каждой из последова-

тельностей можно построить диаграмму Ганта. В результате оказывается, что наимень-

шую длительность обработки (56 мин.) дает правило №1, следующее по длительности (57

мин.) − правило №3.

Нижняя (т.е. минимальная) оценка для общей длительности обработки всех деталей

может быть получена путем сравнения суммарной длительности обработки деталей на

каждом из станков (последняя графа табл. 6.5). Очевидно, что полная длительность обра-

ботки деталей на всех станках будет не меньше максимальной из этих величин при любом

порядке запуска (т.е. для данного примера эта оценка составит T ≥ 37 мин.).

Таблица 6.6. Последовательность запуска деталей

Правило № Последовательность запуска деталей

1 7, 6, 5, 2, 3, 4, 1

2 1, 4, 7, 3, 6, 2, 5

3 7, 6, 2, 3, 5, 4, 1

4 4, 1, 3, 2, 5, 7, 6

В частном случае, когда «узким местом» для всех деталей является один и тот же

станок, найдено соотношение между наибольшей возможной длительностью обработки

всех деталей T

max

и наименьшей длительностью их обработки T

min

, достигаемой при опти-

мальном порядке запуска. Введем следующую величину:

min

minmax

−

=δ .

Тогда для станка, являющегося «узким местом» для всех деталей, отыщем детали,

обработка которых на нем занимает наибольшее τ

max

и наименьшее τ

min

время. Для вве-

денных величин известно, что

min

max

δ ⋅

−

≤

Это неравенство, в сочетании с рассмотренными выше рекомендациями относи-

тельно определения порядка запуска, позволяет оценить возможности улучшения распи-

сания по сравнению с уже достигнутыми результатами.

Наиболее известным и эффективным формализованным методом реше-

ния задачи по отысканию очередности запуска деталей для нескольких стан-

ков является метод ветвей и границ. Это комбинаторный метод, обеспечи-

вающий упорядоченный перебор вариантов и рассмотрение тех из них, кото-

рые признаны перспективными по определенным признакам. Графически пе-

ребор можно представить в виде дерева, корнем которого является все мно-

жество вариантов, а вершины дерева − подмножества частично упорядочен-

ных вариантов решения. Сначала вершины просматриваются, и каждая из

них оценивается. Для вершины, получившей лучшую оценку, ветвление про-

должается. При этом основная трудность заключается в получении этой

оценки [19].

Каждой вершине соответствует множество вариантов решений. Каж-

дому варианту решения соответствует определенное значение критерия эф-

фективности w(x). Лучшее из этих значений (минимальное или максималь-

ное) удобно взять в качестве оценки вершины. Однако подсчитать точное

значение w, не перебрав всех вариантов, невозможно. Поэтому используется

не точное значение w, а его оценка снизу (при минимизации) или сверху (при

максимизации). Оценку снизу называют оценкой нижней границы, оценку

сверху − оценкой верхней границы множества вариантов.

Оценка вершины должна удовлетворять следующим свойствам:

1. Оценка не должна быть больше (при минимизации) или меньше

(при максимизации) минимального (максимального) значения

функции w для данного подмножества вариантов.

2. Значение оценки для подмножеств нижнего уровня не должно быть

меньше (при минимизации) или больше (при максимизации) значе-

ния оценки для подмножеств более высокого уровня.

3. Оценка единственного варианта решения на последнем уровне точ-

но совпадает со значением функции w для этого решения.

Укрупненный алгоритм метода ветвей и границ включает в себя сле-

дующие шаги:

1. Строятся вершины первого уровня. Для каждой вершины подсчи-

тывается оценка нижней (верхней) границы. Ветвится вершина, ко-

торой соответствует лучшая (минимальная или максимальная)

оценка.

2. Для всех вершин i-го уровня (i=2, 3, …) подсчитывается оценка.

Ветвится та из висячих вершин уровня i, i-1, …, 1, которой соответ-

ствует лучшая (минимальная или максимальная) оценка.

3. Действия шага 2 повторяются до тех пор, пока не будет получено

точное решение на последнем уровне. Для него подсчитывается

точное значение w. Если это значение не хуже оценок оставшихся

висячих вершин, то найдено оптимальное решение. Если это значе-

ние строго лучше, то оптимальное решение единственное. Если

значение функции w для висячих вершин последнего уровня не

лучше значения оценок оставшихся висячих вершин, то переходят

на шаг 2.

Метод ветвей и границ не гарантирует того, что в ходе решения задачи

не будет произведен полный перебор вариантов решений.

Модификации метода ветвей и границ используются для решения раз-

личных задач управления производством, включая уже названную задачу о

нахождении оптимального варианта запуска деталей в обработку, задачу о

балансировании сборочной линии (например, при сборке корпусной мебели),

задачу о переналадке станков и другие.

6.2. Оптимальный выбор технологического оборудования для

производства цельных клееных заготовок

Задача оптимального выбора технологического оборудования для про-

изводства цельных клееных заготовок предполагает рассмотрение и анализ

множества проектных решений. Для его формирования может быть исполь-

зован метод вариантного проектирования, основывающийся на следующих

двух предпосылках [20]:

1) объект проектирования представляет собой некоторое число фраг-

ментов различного типа, соединенных в определенном порядке. На-

пример, при рассмотрении в качестве объекта проектирования уча-

стка по производству фанеры можно выделить фрагмент (станок)

для нанесения клея на шпон при сборке пакета, фрагмент для хо-

лодной подпрессовки стопы, фрагмент загрузки пресса, фрагмент

склеивания листов фанеры под прессом, фрагмент разгрузки пресса;

2) каждый из фрагментов, входящих в объект проектирования, может

существовать и применяться в виде нескольких модификаций, оди-

наковых с точки зрения назначения и выполняемых функций, но от-

личающихся технико-экономическими характеристиками (стоимо-

стью, производительностью, энергопотреблением и другими). На-

пример, клеильный пресс, являющийся фрагментом участка по про-

изводству фанеры, может быть представлен различными модифика-

циями: П17Б, ДА4438, Д4038 и другие [21].

Таким образом, комбинируя фрагменты в различных допустимых соче-

таниях в соответствии с правилами вхождения каждого фрагмента в объект

проектирования, можно получать различные варианты объекта проектирова-

ния.

Наиболее простой способ синтеза вариантов объекта проектирования

на основе представленных фрагментов заключается в полном переборе вари-

антов. Их число ограничено, поскольку ограничено число вариантов каждого

фрагмента. Процесс синтеза вариантов объекта проектирования из фрагмен-

тов можно проиллюстрировать с помощью так называемого дерева синтеза.

Каждый из вариантов первого фрагмента объединяется с каждым из

вариантов второго фрагмента, далее каждое из полученных парных объеди-

нений объединяется с каждым вариантом третьего фрагмента и т.д.

Предположим, требуется получить все варианты комплектования обо-

рудованием производственного участка деревообработки. Известно, что уча-

сток включает три технологических узла (фрагмента), причем первый фраг-

мент может быть реализован в двух вариантах, второй и третий фрагменты −

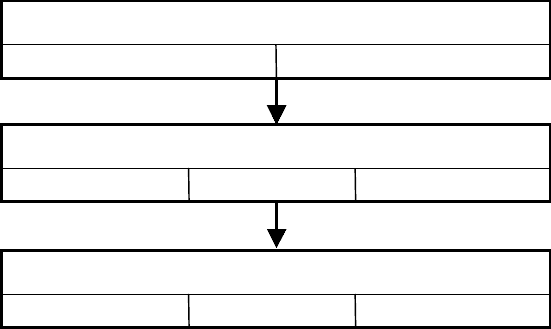
в трех вариантах (рис. 6.3).

Первый фрагмент

−

2 варианта, M(1)=2

й вариант 2

й вариант

Второй фрагмент

−

3 варианта, M(2)=3

й вариант 2

й вариант 3

й вариант

Третий фрагмент

−

3 варианта, M(3)=3

вариант 2

й вариант 3

й вариант

Рис. 6.3. Структурная схема задачи синтеза вариантов решений

Соответствующее данной структурной схеме дерево синтеза представ-

лено на рис. 6.4. В кружках, обозначающих вершины дерева, записаны струк-

турные коды вариантов. Порядковый номер цифры в коде соответствует но-