Бунаков П.Ю., Рудин Ю.И., Стариков А.В. Основы автоматизированного проектирования изделий и технологических процессов
Подождите немного. Документ загружается.


71
Заменим производную конечной разностью
x
xyxxy
dx
xdy
∆
−
∆
+
=
)()()(
и подставим
ее в исходное уравнение: 0)(
)()(
=++
∆
−
∆
+
cxby
x
xyxxy
a . Отсюда
a
cxybx
xyxxy
))((
)()(
+
⋅
⋅
∆
−=∆+ . Это и есть конечно-разностное уравнение, позво-
ляющее найти приближенное решение исходного дифференциального уравнения, зная
значения этого решения в некоторых узловых точках.
Макроуровень использует представление о среде как о дискретном
пространстве, т.е. он предполагает такую степень детализации описания объ-
ектов, которая позволяет рассматривать физические процессы протекающи-
ми в непрерывном времени и дискретном пространстве. Элементами этого
уровня являются те объекты, которые на микроуровне рассматривались как
системы. Здесь же они сосредоточены в определенных точках и связаны ме-
жду собой. Например, рассмотрим материнскую плату компьютера. Макро-
уровень ее описания – принципиальная схема, элементами которой являются
транзисторы, резисторы, интегральные микросхемы, конденсаторы и т.д. На
микроуровне были детально изучены свойства всех этих элементов, поэтому
здесь они представляются точками дискретного пространства.
При формировании математических моделей на макроуровне исполь-
зуют два типа уравнений: компонентные и топологические.
Компонентными уравнениями называются уравнения, описывающие
свойства элементов (компонентов) системы, а топологическими – их взаи-
мосвязи в моделируемой системе. Для описания поведения системы вводится
понятие вектора фазовых переменных – набора физических величин, пол-
ностью описывающих поведение системы на данном уровне. Различают два
типа фазовых переменных:
• переменные типа потенциала (электрическое напряжение, давле-
ние, температура и т.п.);
• переменные типа потока (электрический ток, расход, тепловой
поток соответственно).
Компонентные уравнения описывают связи между разнотипными фа-
зовыми переменными, которые относятся к одному объекту, например, закон
Ома, который связывает напряжение и силу тока. В общем виде их можно
записать таким образом: F(V)=0, где V=(v
1
,v
2
,…,v
n
) – вектор фазовых пере-
менных. Для закона Ома V=(u,i) и
0
=
⋅
−
Riu
, где R – электрическое сопро-
тивление.
Топологические уравнения описывают связи между однотипными фа-
зовыми переменными в разных компонентах системы и имеют вид
0),,( =t
dt
dV
VF . Примером могут служить законы Кирхгофа для схемы без ис-
точников ЭДС:
• в любом узле электрической схемы сумма входящих токов равна
сумме исходящих токов:
∑
=
j
j
i 0;
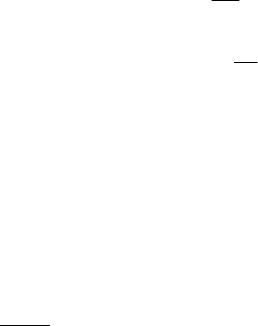
72
• сумма падений напряжений на элементах схемы в любом замкнутом
контуре равна нулю:
∑
=
j
j
u 0.
Одним из основных свойств математических моделей является их уни-
версальность, поэтому компонентные и топологические уравнения для опи-
сания систем различной природы могут иметь одинаковый вид. Таким обра-
зом, в САПР большое количество моделей и алгоритмов их исследования мо-
гут применяться для анализа систем различной физической природы, т.е. они
являются инвариантными. Это особенно удобно при работе с системами,
компоненты которых являются физически разнородными. Для графического
представления подобных систем используются эквивалентные схемы.
Рассмотрим это на примере сопоставления электрических и механиче-
ских систем.
Как отмечалось выше, фазовыми переменными в электрических схемах
являются электрические напряжения и токи. В простейшем случае их компо-
нентами являются простые двухполюсники:
• резисторы (резистивные элементы), характеризующиеся сопротив-
лением R;
• конденсаторы (емкостные элементы), характеризующиеся емкостью
С;
• индуктивности (индуктивные элементы), характеризующиеся одно-
именным параметром L.
Если через u обозначить падение напряжения на двухполюснике, а че-
рез i – протекающий через него ток, то компонентные уравнения будут иметь
вид:
• для резистора:
Riu
⋅
=
;
• для конденсатора:
dt
du
Ci ⋅= ;
• для индуктивности:
dt
di
Lu ⋅= .
Модели более сложных компонентов (многополюсников) можно сфор-
мировать на основе данных моделей. В зависимости от целей исследования
данные уравнения могут иметь более сложный вид, например, если необхо-
димо учесть зависимость сопротивления от температуры ( )1(
0
tRR
t
∆⋅+⋅= α ,
где α – температурный коэффициент сопротивления для данного материала,
Δt=t-t
0
– разность температур), или зависимость емкости от параметров кон-
денсатора (
d
S
С
0
εε
= , где ε
0
– диэлектрическая проницаемость вакуума, ε –
диэлектрическая проницаемость среды, заполняющей пространство между
пластинами, S – площадь пластин, d – расстояние между ними).
Компонентные уравнения выражают законы Кирхгофа и приведены
выше. Фазовыми переменными в механических системах являются сила F и
скорость V. Формально, любую из них можно отнести к переменной типа по-
тенциала, а другую – к переменной типа потока. Более «привычный» вид
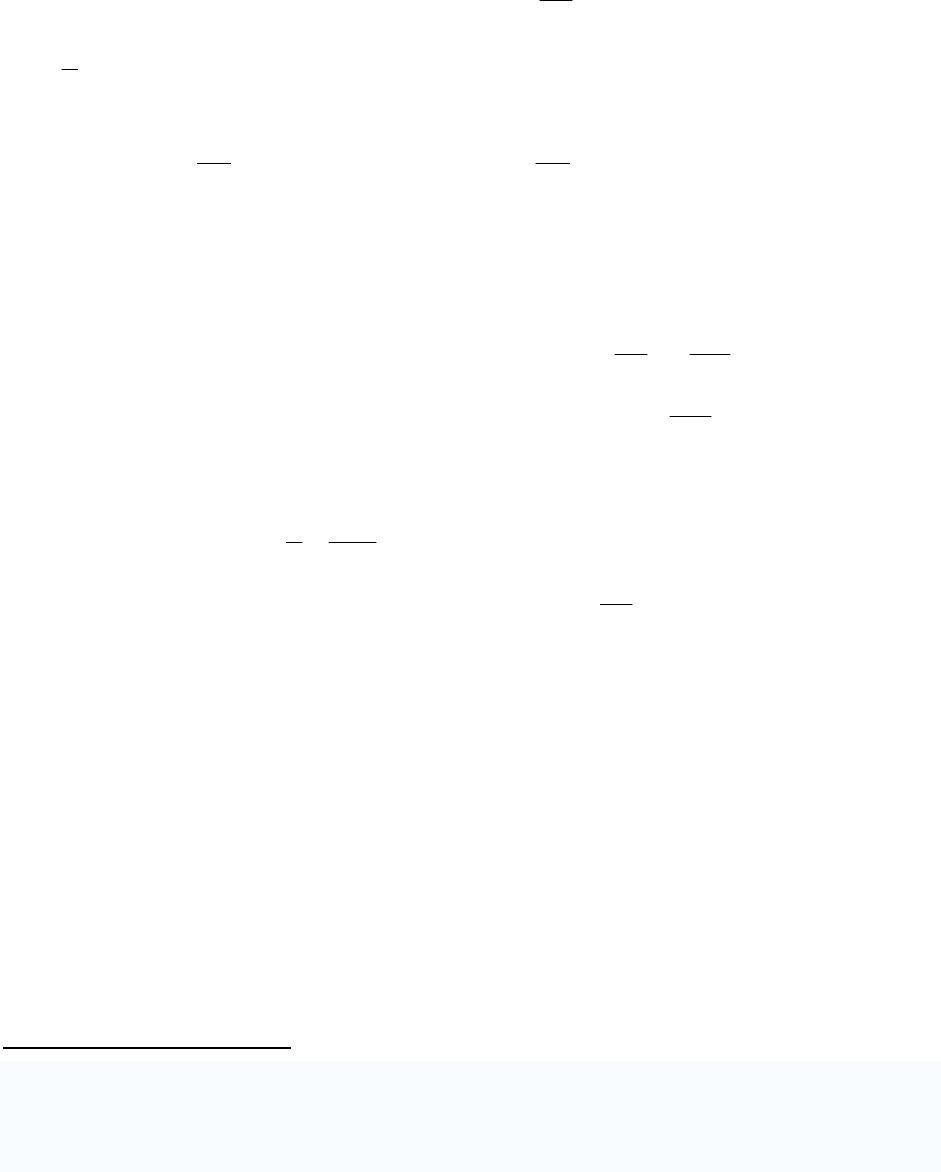
73
компонентные уравнения будут иметь в том случае, если скорость отнести к
потенциалу, а силу – к потоку.
Характеристиками «механических двухполюсников» будут являться:
• трение (аналог сопротивления);
• масса (аналог емкости);
• упругость (аналог индуктивности).
Аналог закона Ома характеризует связь между силой трения и скоро-
стью взаимного перемещения тел:
m
R
V
VkF =⋅= , где k – коэффициент трения,
k
R
m
1
= – механический аналог сопротивления.
Инерционные свойства системы описываются вторым законом Нью-
тона:
dt
dV
mmaF == , где m – масса тела,
dt
dV
a = – ускорение поступательного
движения.
Для вывода третьего компонентного уравнения вернемся к рассмот-
ренному выше закону Гука:
xkF
∆
⋅
=
, который справедлив не только для пру-
жин, но и для продольных деформаций упругого стержня. Продифференци-
ровав обе части уравнения по времени, получим: kV
dt
xd
k
dt
dF
=
∆
= , где k – же-
сткость, Δx – абсолютное удлинение (деформация),
dt
xd
V
∆
= – скорость.
Для того, чтобы привести это уравнение в виду, аналогичному уравне-
нию для индуктивности, вспомним, что величина, обратная жесткости, назы-
вается гибкостью:
E
S
x
k
L
m
⋅
==
1
, где x – длина стержня, S – площадь попереч-
ного сечения, E – модуль упругости. Тогда
dt
dF
LV
m
= .
В таблице 5.2. приведены фазовые переменные и характеристики ком-
понентов для различных предметных областей.
Топологические уравнения для механической системы определяются
двумя законами:
• закон равновесия сил (принцип Даламбера): сумма всех сил, вклю-
чая силу инерции, приложенных к телу, равна нулю – 0=
∑
j
j
F ;
• закон скоростей: сумма абсолютной, относительной и переносной
3
скоростей равна нулю.
Как видно, аналогии между электрическими и механическими систе-
мами очевидны. Однако имеется и существенное отличие: процессы в элек-
трических системах одномерны, а в механических – двух или трехмерны. Для
3
Абсолютная скорость – это скорость движения точки относительно абсолютной системы
отсчёта. Относительная скорость – это скорость движения точки относительно подвижной
системы отсчёта. Переносная скорость — это скорость движения точки, обусловленная
движением подвижной системы отсчёта относительно абсолютной.
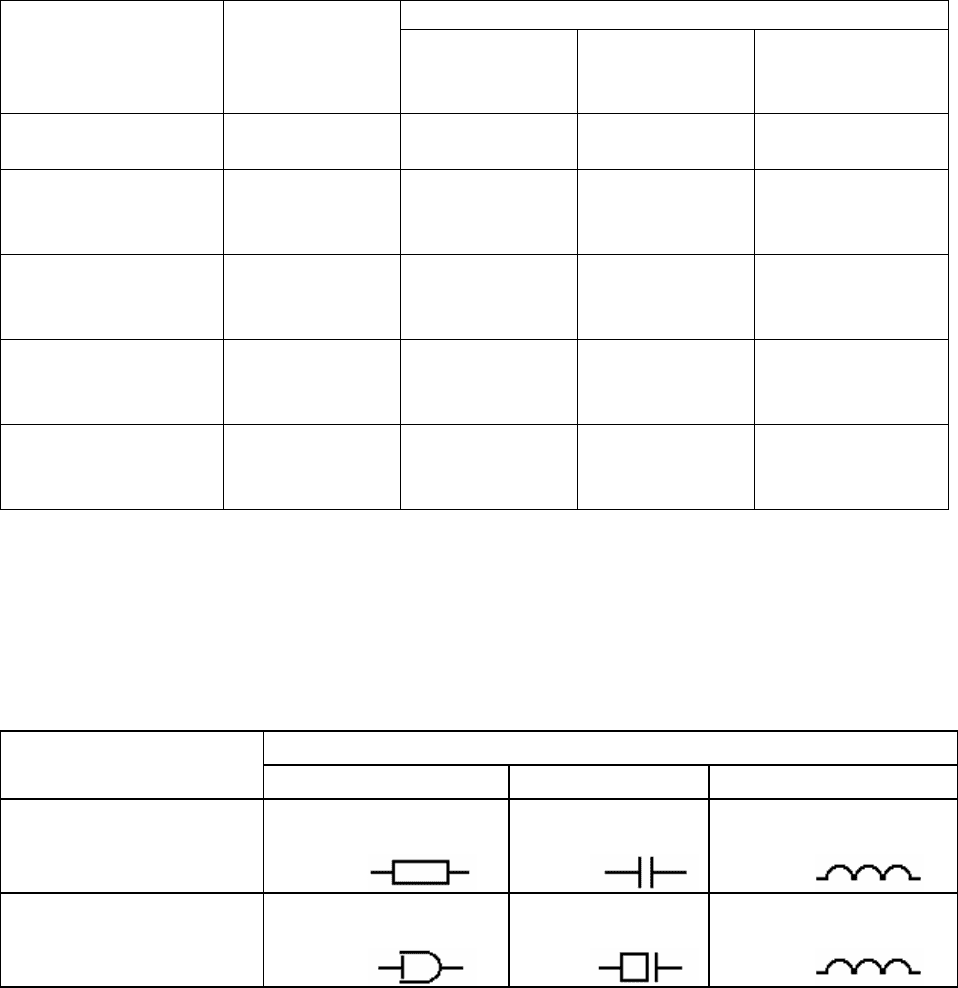
74
того чтобы остаться в рамках рассмотренных аналогий, следует рассматри-
вать проекции сил и скоростей на пространственные оси координат.
Подобные аналогии можно провести и по отношению к другим пред-
метным областям.
Таблица 5.2. Фазовые переменные и характеристики компонентов
Характеристики-аналоги
Область
применения
Фазовые
переменные
резистивные
емкостные
индуктивные
Электрические
схемы
ток,
напряжение
сопротивление
емкость индуктивность
Механическое
поступательное
движение
сила,
скорость
трение масса упругость
Механическое
вращательное
движение
момент,
угловая
скорость
трение
момент
инерции
вращательная
гибкость
Потенциальное те-
чение
расход,
давление
трение гидравличе-
ская
емкость
гидравлическая
индуктивность
Теплотехника тепловой
поток,
температура
тепловое
сопротивление
теплоемкость
–
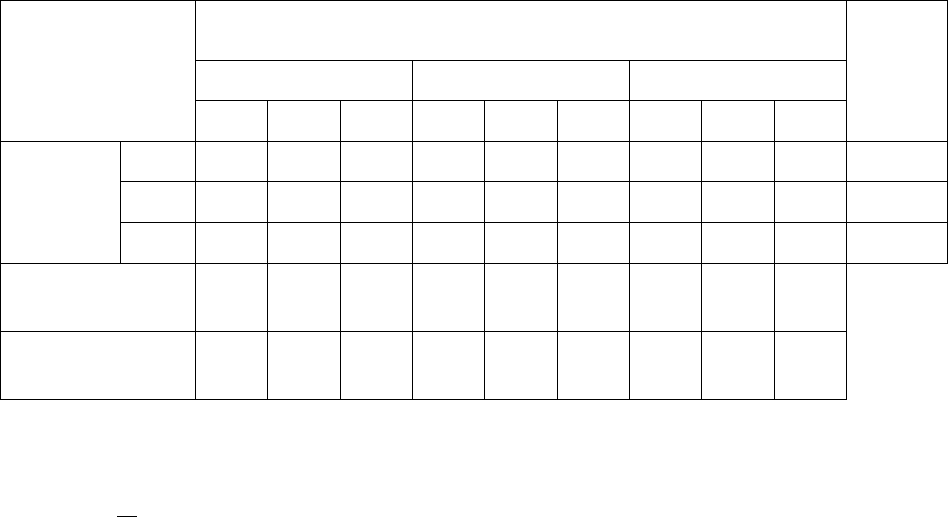
Для графического представления моделей на макроуровне используют-
ся эквивалентные схемы, в которых обозначения резистивных, емкостных и
индуктивных элементов соответствуют области моделирования. Пример по-
добных обозначений для электрических и механических систем приведен в
таблице 5.3.
Таблица 5.2. Соответствие электрических и механических компонентов
Условные обозначения Область применения
резистивные емкостные индуктивные
Электрическая сопротивление
R
емкость
C
индуктивность
L
Механическая сухое трение
R
M
масса
m
гибкость
L
M
Наличие подробных аналогий позволяет моделировать системы, со-
стоящие из компонентов различной физической природы. Для этого выпол-
няется следующая последовательность шагов:
• выделение в системе физически однородных подсистем (механиче-
ских, гидравлических, электрических и т.п.);
• построение эквивалентных схем для каждой из подсистем;
• установление связей между подсистемами;
• построение математической модели системы.

75
С ростом числа элементов размерность задачи вырастает и становится
необходимым переход к следующему иерархическому уровню − метауровню.
На метауровне используется такая степень детализации описания
сложных систем, при которой процессы, протекающие в самих системах, рас-
сматриваются в минимальной степени. Объектами исследования на этом
уровне являются сложные устройства и комплексы, функционирование кото-
рых рассматривается как последовательность событий, происходящих в дис-
кретные моменты времени и заключающиеся в изменении состояния элемен-
тов. Другими словами, метауровень использует дискретное представление,
как о пространстве, так и о времени, а его элементами являются системы мак-
роуровня.
Для моделирования на метауровне используются обыкновенные диф-
ференциальные уравнения, модели массового обслуживания
4
, логические
уравнения, теорию графов. Одним из наиболее общих подходов к анализу
объектов на метауровне является использование аппарата передаточных
функций, примером применения которого является функциональное модели-
рование систем автоматического управления (САУ).
Передаточная функция – представляет собой один из способов
математического описания динамической системы. Она представляет собой
отношение преобразования Лапласа
5
выходного сигнала к преобразованию
Лапласа входного сигнала при нулевых начальных условиях. В теории авто-
матического управления рассматриваются структурные схемы автоматиче-
ских систем, состоящие из динамических звеньев с известными передаточ-
ными функциями. Передаточная функция является основной характеристи-
кой звена в динамическом режиме, из которой можно получить все осталь-
ные характеристики. Она определяется только параметрами системы и не за-
висит от входных и выходных величин.
Таким образом, независимо от физической природы динамического
звена для любого входного сигнала можно определить выходной сигнал:
X
вых
(p)=X
вх
(p)W(p), и задача расчета САУ сводится к определению ее переда-
4
Теория массового обслуживания – это математическая дисциплина, изучающая системы,
предназначенные для обслуживания массового потока требований случайного характера.
Типичный пример объекта массового обслуживания является автоматическая телефонная
станция, на которую случайным образом поступают вызовы абонентов, а «обслуживание»
заключается в соединении абонентов между собой, поддержании связи во время сеанса,
переадресации вызовов и т.д.
5
Преобразование Лапласа – это интегральное преобразование, связывающее функцию
комплексного переменного F(p) (изображение по Лапласу) с функцией f(t) (оригинал) со-
отношением:
∫
∞
−
=
0
)()( dttfepF
pt
, где p=a + jb – комплексное число. Одной из особенно-
стей преобразования Лапласа, предопределившей его широкое распространение в науч-
ных и инженерных расчётах, является то, что многим сложным операциям над оригина-
лами соответствуют более простые операции над их изображениями.
76
точной функции. Если элемент имеет более одного входа и выхода, то вместо
скалярных сигналов используются векторы.
Моделирование систем на метауровне с помощью аппарата передаточ-
ных функций сводится к следующей последовательности операций:
• представление системы в виде совокупности звеньев, передаточные
функции которых известны;
• формирование передаточной функции системы по передаточным
функциям звеньев;
• преобразование по Лапласу входных сигналов;
• нахождение решения системы алгебраических уравнений, которое
представляет собой изображения выходных сигналов;
• нахождение оригиналов выходных сигналов при помощи обратного
преобразования Лапласа.
Если элемент имеет более одного входа и выхода, то вместо скалярных
сигналов используются векторы.
Вопросы для контроля
1. В чем состоит различие между объектом и моделью? Назовите основные
свойства математических моделей.
2. В чем заключаются преимущества и недостатки математического модели-
рования перед экспериментальными исследованиями?
3. Какие требования предъявляются к математическим моделям?
4. Дайте характеристики аналитических геометрических моделей, применяе-
мых в САПР.
5. Расскажите об основных методах формирования твердотельных моделей в
САПР без использования прямого математического описания.
6. Как классифицируются математические модели по уровню абстракции?
7. Что такое микроуровень моделирования?
8. Что такое макроуровень моделирования?
9. Что такое метауровень моделирования?
Глава 6
Некоторые задачи моделирования и оптимизации
технологических процессов деревообработки
В данной главе рассмотрены частные задачи, связанные с моделирова-
нием и оптимизацией управления технологическими процессами деревооб-
работки, а также общие подходы, методы и практические рекомендации к их
решению.
77
6.1. Задача оптимальной загрузки деревообрабатывающего
оборудования
Задача оптимальной загрузки деревообрабатывающего оборудования
может быть решена с использованием моделей и методов математического
программирования − одного из наиболее разработанных разделов комплекс-
ной научной дисциплины «Исследования операций».
Общая постановка задачи об использовании производственных
мощностей (загрузке оборудования)
Производственное предприятие имеет различные виды технологиче-
ского оборудования. При решении задачи об использовании производствен-
ных мощностей необходимо различать невзаимозаменяемое (специализиро-
ванное) оборудование, реализующее только один вид технологии, и взаимо-
заменяемое (универсальное) оборудование, способное перестраиваться с од-
ного вида технологии на другой. Модели оптимального использования про-
изводственных мощностей для этих видов оборудования принципиально раз-
личаются.
Модель оптимальной загрузки невзаимозаменяемых групп
оборудования
Для построения математической модели для задачи оптимальной за-
грузки невзаимозаменяемых групп оборудования введем следующие обозна-
чения [15]:
i −
вид производимой продукции;
l −
количество видов производимой продукции;
j −
вид технологии;
n −
количество видов технологии;
ij
p −
прибыль, получаемая от реализации единицы продукции i-го
вида, произведенной по j-й технологии;
r −
вид технологического оборудования;
R −
количество видов технологического оборудования;
r
b −
полезное время работы оборудования r-го вида;
r
ij
a
−
норма расхода машинного времени для оборудования r-го вида
при изготовлении единицы продукции i-го вида по j-й техноло-
гии;
ij
x −
количество продукции i-го вида, производимого по j-й техноло-
гии.

78
В общем случае задачей моделирования является поиск величин x
ij
, оп-
ределяющих такое распределение объема производимой продукции по ее ви-
дам и по видам технологии изготовления, при котором обеспечивается мак-
симум прибыли при существующих ограничениях на полезное время работы
оборудования (при ограничениях
r
b ).
Математическая модель задачи может быть записана в следующем
кратком виде:
∑∑
= =
→
l
i
n
j
ijij
xp
1 1
max, ( li ,1= ; nj ,1= ); (6.1)
∑∑
= =
≤
l
i
n
j
rij
r
ij
bxa
1 1
, ( Rr ,1= ); (6.2)
.0
≥
ij
x (6.3)
Элементами данной модели являются выражение для целевой функции
(6.1), выступающее в качестве критерия оптимальности (эффективности) ре-
шения задачи, а также системы функциональных (6.2) и тривиальных (6.3)
ограничений, задающих область допустимых решений (ОДР) задачи.
Приведенная выше модель является формальным представлением
двухиндексной задачи линейного программирования (ЗЛП), решение которой
− оптимальный (по прибыли) план {x
ij
} загрузки невзаимозаменяемого обо-
рудования предприятия. В условиях рыночной экономики такой подход к оп-
тимизации выпуска продукции целесообразен, если, конечно, нет ограниче-
ний на возможности реализации производимой продукции (что само по себе
является существенным упрощением реальной ситуации).
Модель загрузки невзаимозаменяемого оборудования может быть
представлена в другой постановке, когда ограничениями являются объемы
выпускаемой продукции i-го вида:
i
n
j
ij
Qx ≥
∑
=1
, ( li ,1= ) (6.4)
и задано ограничение на полезное машинное время b
r
∑∑
= =
≤
l
i
n
j
rij
r
ij
bxa
1 1
, ( Rr ,1= ). (6.5)
Критерием оптимального плана выпуска продукции будет минимиза-
ция затрат на выпуск заданного объема продукции:
∑∑
= =
→
l
i
n
j
ijij
xc
1 1
min , (6.6)
где c
ij
− стоимость затрат на производство единицы i-го вида продукции
по j-й технологии; Q
i
− плановое задание выпуска продукции i-го вида.
79
Пример 6.1. На мебельной фабрике имеются три невзаимозаменяемые группы обо-
рудования (R=3), на котором изготавливаются три вида конечной продукции (l=3) с ис-
пользованием трех видов технологии (n=3). Каждый вид оборудования в зависимости от
вида продукции имеет свои нормативные коэффициенты
r
ij
a
расхода машинного времени
на изготовление единицы i-го вида продукции по j-й технологии. Возможности изготовле-
ния определенной продукции на конкретном оборудовании в виде нормативных коэффи-
циентов
r
ij
a
, обеспечиваемой прибыли
ij
p на единицу продукции, ограничения по ма-
шинному времени
r
b представлены в табл. 6.1.
Таблица 6.1. Показатели производства продукции на определенном виде
оборудования
Нормативные коэффициенты
r
ij
a
i = 1 i = 2 i = 3
Наименование
показателей
j=1 j=2 j=3 j=1 j=2 j=3 j=1 j=2 j=3
b
r
,
сотни
станко-
час.
r = 1 2 2 1 3 0 4 3 3 0 20
r = 2 3 1 2 1 2 0 5 6 0 34
Группы
оборудо-
вания
r = 3 0 1 3 2 3 1 1 0 0 48
Прибыль p
ij
,
сотни рублей
11 7 5 9 6 7 18 15 0
Выпуск продук-
ции, шт.
x
11
x
12
x
13
x
21
x
22
x
23
x
31
x
32
x
33
Составим математическую модель задачи. Используя формулу (6.1) и введя соот-
ветствующие обозначения для неизвестных (управляющих) переменных x
ij
(последняя
строка табл. 6.1), запишем выражение для целевой функции задачи:
max015187695711)(
333231232221131211
→++++++++= xxxxxxxxxXW .
Далее запишем систему линейных неравенств (формула 8.2), определяющих огра-
ничения по полезному времени
r
b работы оборудования каждого вида:
≤++++++++
≤++++++++
≤++++++++
.48001132310
,34065021213
,20033403122
333231232221131211
333231312321131211
333231232221131211
xxxxxxxxx
xxxxxxxxx
xxxxxxxxx
Кроме того, необходимо задать тривиальные (естественные) ограничения (формула
8.3) как систему неравенств следующего вида:
≥≥≥
≥≥≥
≥≥≥
.0,0,0
,0,0,0
,0,0,0
333231
232221
131211
xxx
xxx
xxx
Дополнительно на неизвестные переменные x
ij
должно накладываться ограничение (усло-
вие) целочисленности, поскольку выпускается целое количество мебельных изделий:
Zx
ij
∈
.
Поставленная задача может быть решена с помощью симплекс-
метода − универсального метода для решения задач линейного программиро-
вания. Симплекс-метод имеет множество программных реализаций (в том
80
числе и известных), он также представлен в процедуре «Поиск решения»
(Solver), использующейся в составе процессора электронных таблиц Microsoft
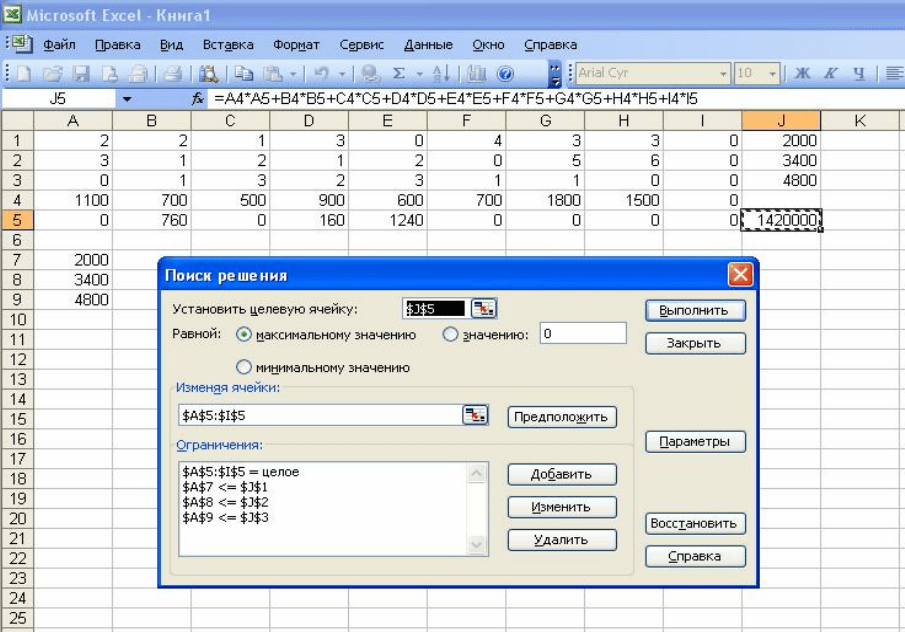
Excel. Результат расчета модели в Microsoft Excel показан на рис. 6.1.
Рис. 6.1. Расчет модели с использованием процедуры «Поиск решения»
Компьютерная модель, представляющая собой электронную таблицу,
содержит как исходные данные задачи (значения
r
ij
a
− ячейки A1:I3,
r
b −
ячейки J1:J3,
ij
p − ячейки A4:I4), так и формулы − выражения для целевой
функции (ячейка J5) и функциональных ограничений (ячейки A7:A9).
В диалоговом окне процедуры «Поиск решения» задаются необходи-
мые параметры, включая ограничения модели, ее линейность и положитель-
ность искомых величин. После расчета в ячейках A5:I5 представлены значе-
ния искомых величин x
ij
, в данном случае − x
12
= 760, x
21
= 160, x
22
= 1240, ос-
тальные величины имеют нулевые значения. В целевой ячейке отображается
максимальное значение прибыли − 1 млн 420 тыс. рублей.
Модель оптимальной загрузки технологического оборудования может
иметь ряд отличий, отражающих особенности конкретной производственной
ситуации. Ниже рассмотрены две подобные модели: выбор технологий, обес-
печивающих минимум затрат при выполнении заказа, и максимизация объе-
ма комплектной продукции с учетом возможностей оборудования.
