Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.


51
Пояснения.
Последнее утверждение говорит о том, что, если имеются экстремумы,
то в функции Лагранжа учитывается соответствующая им целевая функция, а
не одни только ограничения.
Точки
x
называются условно-стационарными (так как рассматривается
условная оптимизация, в отличие от случая безусловной оптимизации, когда
они называются просто стационарными).
Далее вводится понятие индекса ограничений
a
J , активных в точке
x
(номера ограничений-неравенств, которые стали равенствами в точке
x
).
Достаточные условия экстремума первого порядка в задаче услов-
ной оптимизации с ограничениями-неравенствами
Пусть имеется точка ),(
x , удовлетворяющая необходимым условиям
экстремума первого порядка (рассмотренным выше) при 0
0
, число ак-
тивных ограничений в точке
x
совпадает с числом
n
переменных (при этом
условие регулярности выполняется). Если 0
j
для всех
a
Jj
, то точка
x
— условный локальный минимум. Если 0
j
для всех
a
Jj
, то точка
x
— условный локальный максимум.
Необходимые условия экстремума второго порядка в задаче услов-
ной оптимизации с ограничениями-неравенствами
Пусть
x
— регулярная точка экстремума в задаче условной оптимиза-
ции и имеется решение ),(
x , удовлетворяющее необходимым условиям
экстремума первого порядка. Тогда второй дифференциал классической
функции Лагранжа в точке ),(
x неотрицателен для минимума:
0),(
2
xLd
и неположителен для максимума:
0),(
2
xLd
для всех первых дифференциалов
n
R
x
d
таких, что
0)(
xdq
j
,
a
Jj
при 0
j
для минимума и 0
j
для максимума,
0)(
xdq
j
,
a
Jj
при 0
j
.

52
Достаточные условия экстремума второго порядка в задаче услов-
ной оптимизации с ограничениями-неравенствами
Пусть имеется точка ),(
x , удовлетворяющая необходимым условиям
экстремума первого порядка (рассмотренным выше) при 0
0
. Если в этой
точке 0),(
2
xLd , то для всех ненулевых
n
R
x
d
таких, что
0)(
xdq
j
,
a
Jj
при 0
j
для минимума и 0
j
для максимума,
0)(
xdq
j
,
a
Jj
при 0
j
,
то точка
x
— локальный минимум (максимум).
Алгоритм решения задачи условной оптимизации при ограничени-
ях-неравенствах
Исходные данные: вектор искомых переменных
x
размерности
n
, целе-
вая функция
)
(
x
I
и функции-ограничения в форме неравенств 0)(
xq
j
,
m
j
,
,
1
.
Шаг 1. Составляется обобщённая функция Лагранжа
m
j
jj
xqxIxL
1
00
)()(),,(
.
Шаг 2. Записываются необходимые условия экстремума первого поряд-
ка:
.,,1,0)(
;,,1(max),0(min),0
;,,1,0)(
;,,1,0
),,(
0
mjxq
mj
mjxq
ni
x
xL
j
jj
j
i
Шаг 3. Решается полученная система уравнений для двух случаев:
1) 0
0
;
2) 0
0
, для чего первое условие шага 2 делится на
0
и производится
замена переменных
0
j
на новые
j
.
В результате находятся значения
x
и
, соответствующие условно-
стационарным точкам
x
, которых в общем случае может быть несколько.
Из них выделяются те, что найдены при условии 0
0
— эти точки могут
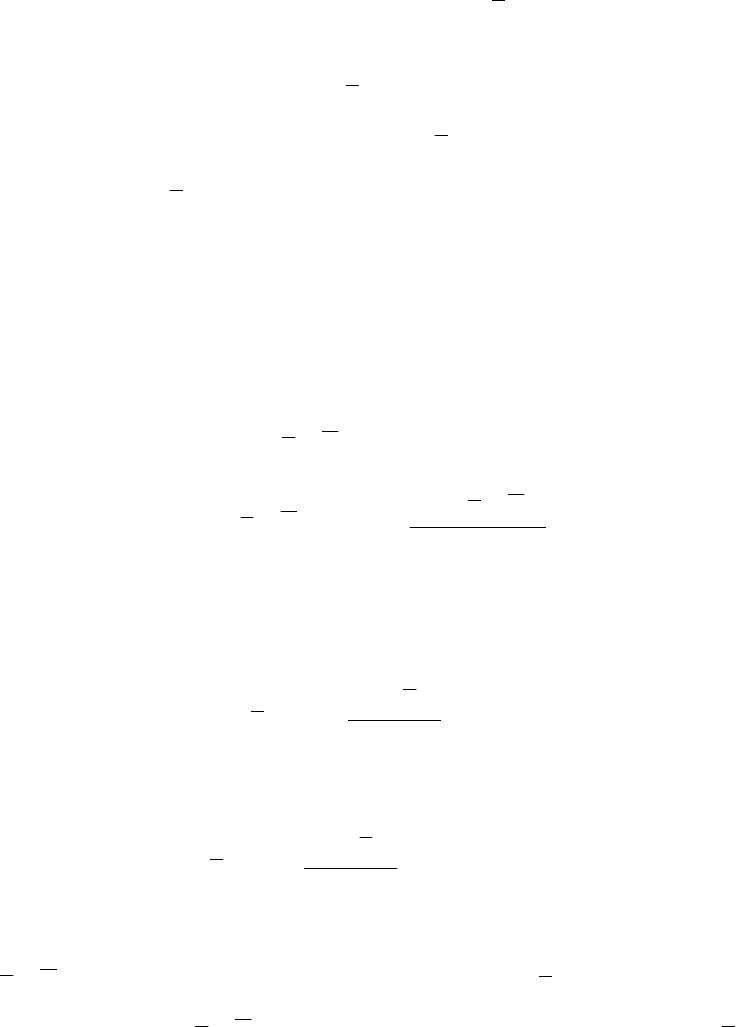
53
быть регулярными точками экстремума, что необходимо проверить с помо-
щью достаточных условий.
Шаг 4. Для выделенных на шаге 3 точек проверяются достаточные
условия экстремума следующим образом:
а) определяют число
l
активных в точке
x
ограничений;
б) если
n
l
(т. е. число активных ограничений, превратившихся в урав-
нения, равно числу переменных
x
) и для всех
a
Jj
(т. е. для всех актив-
ных ограничений) 0
j
, то в точке
x
— локальный минимум, а если
0
j
, то в точке
x
— локальный максимум; если
n
l
или соответствую-
щие множители Лагранжа не удовлетворяют достаточным условиям первого
порядка, следует проверить достаточные условия второго порядка.
Для проверки достаточных условий второго порядка выполняются сле-
дующие действия:
а) записывается выражение для второго дифференциала классической
функции Лагранжа в точке ),(
x :
ji
n
i
n
j
ji
dxdx
xx
xL
xLd
1 1
2
2
),(
),(
;
б) записывается система уравнений для первого дифференциала функ-
ций ограничений:
0
)(
)(
1
i
n
i
i
j
j
dx
x
xq
xdq ,
a
Jj
,
при 0
j
для минимума и 0
j
для максимума,
0
)(
)(
1
i
n
i
i
j
j
dx
x
xq
xdq ,
a
Jj
, 0
j
в) осуществляется проверка знака второго дифференциала: если
0),(
2
xLd при ненулевых
i
dx , то в точке
x
— условный локальный
минимум; если 0),(
2
xLd при ненулевых
i
dx , то в точке
x
— услов-
ный локальный максимум.
Если достаточные условия экстремума первого и второго порядков не
выполняются, то следует проверить выполнение необходимых условий вто-
рого порядка по аналогичной процедуре. Если они выполняются, то требу-
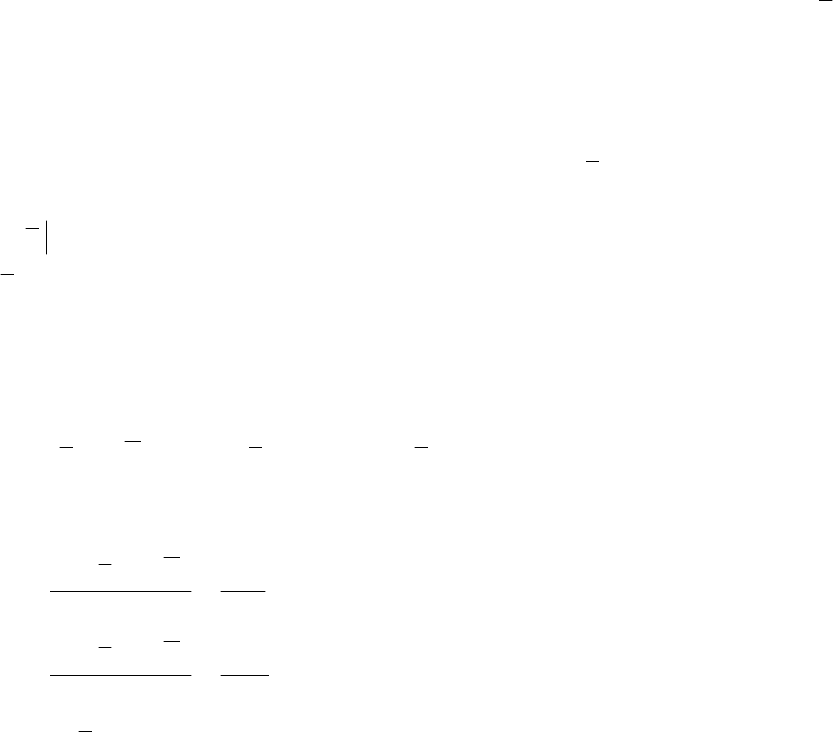
54
ются дополнительные исследования, если не выполняются — в точке
x
нет
условного экстремума.
Шаг 5. Если точки условного экстремума найдены, в них вычисляются
значения целевой функции.
Пример 4.7. Пусть задана целевая функция
2
2
2
1
)( xxxI на множестве
02
21
xxxX , т. е. задано одно ограничение-неравенство
02)(
211
xxxq , причём здесь
2
n
,
1
m
.
Решение.
1. Составляется обобщённая функция Лагранжа:
)2()()()(),,(
211
2
2
2
10
1
1
00
xxxxxqxIxL
j
jj
.
2. Выписываются необходимые условия экстремума первого порядка:
а)
;022)(
),,(
;022)(
),,(
120211
2
2
2
10
2
2
0
110211
2
2
2
10
11
0
xxxxx
xx
xL
xxxxx
xx
xL
б) 02)(
21
xxxq .
Таким образом, получена система уравнений и неравенств:
,0)2(
(max);0
(min);0
;02
;02
;02
211
1
1
21
120
110
xx
xx
x
x
для которой ищется решение.
3. Решение системы может быть получено для двух случаев: для 0
0
и 0
0
.
В первом случае принимается 0
0
. тогда из первого условия системы
следует, что:
002
11
x , 0
1
,

55
что противоречит необходимому условию условного экстремума первого по-
рядка о существовании ненулевого вектора, состоящего из
0
и
, поэтому
допущение о 0
0
неверное.
Во втором случае 0
0
. Тогда можно перейти от обобщённой к клас-
сической функции Лагранжа, поделив её на
0
и заменив
0
j
на новые
j
:
;022)(
),(
;022)(
),(
12211
2
2
2
1
22
11211
2
2
2
1
11
xxxxx
xx
xL
xxxxx
xx
xL
Тогда новая система уравнений и неравенств будет иметь вид:
.0)2(
(max);0
(min);0
;02
;02
;02
211
1
1
21
12
11
xx
xx
x
x
В результате из уравнений исчезла одна переменная —
0
.
Из условия дополняющей нежёсткости
0)2()(
21111
xxxq
,
следует:
1) если 0
1
(т. е. фактически ищется безусловный экстремум, так как
единственный коэффициент Лагранжа
1
обнуляет единственное ограниче-
ние), тогда решение: 0022
111
xx
, 0
1
x , 0022
212
xx
,
0
2
x , 0
1
;
2) если 0
1
, то должно выполняться условие 0)2()(
211
xxxq ,
поэтому система уравнений принимает вид:
,02
;02
;02
21
12
11
xx
x
x
откуда находится решение: 1
1
x , 1
2
x , 2
1
.
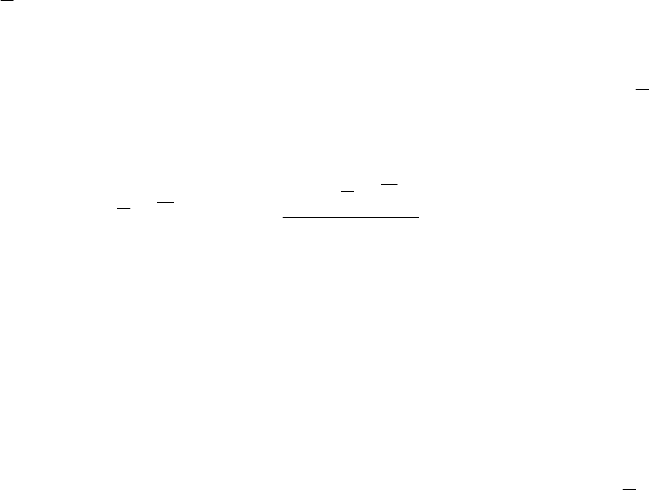
56
По знаку коэффициента
1
можно определить вид возможного экстре-
мума (точнее, исключить какой-либо вид): поскольку знак отрицательный,
это не может быть минимум, но, возможно, максимум. Окончательное суж-
дение связано с проверкой достаточных условий.
4. Проверяются достаточные условия экстремума.
Вначале используются достаточные условия первого порядка. Одним из
условий является активность ограничений в точке предполагаемого экстре-
мума.
Рассматривается условие 0
1
. В соответствующей этому условию
точке 0
1
x , 0
2
x ограничение имеет вид: 022002
21
xx ,
т. е. не является активным (не превращается в равенство). Поэтому в соответ-
ствии с достаточными условиями первого порядка нельзя утверждать, что
точка
T
x )0,0(
является экстремумом. Следует проверить её по достаточ-
ным условиям второго порядка, в соответствии с которыми анализируется
знак второго дифференциала функции Лагранжа. В точке
T
x )0,0(
второй
дифференциал имеет вид:
022
),(
),(
2
2
2
1
2
1
2
1
2
2
dxdxdxdx
xx
xL
xLd
ji
i j
ji
,
его положительность обусловлена тем, что он равен сумме квадратов диф-
ференциалов, а квадраты, как и любые чётные степени — всегда неотрица-
тельны, причём с учётом ненулевых первых дифференциалах 0
1
dx , 0
2
dx
он оказывается не только неотрицательным, но строго положительным.
В соответствии с достаточными условиями второго порядка положи-
тельность второго дифференциала означает, что в точке
T
x )0,0(
имеется
локальный минимум (отрицательность означала бы максимум). Но эта точка
совпадает с глобальным минимумом (если бы отсутствовало ограничение),
что связано с принятым условием 0
1
(в соответствии с которым ограни-
чение в функции Лагранжа обнуляется).
Далее рассматривается случай с 0
1
. В соответствующей этому усло-
вию точке 1
1
x , 1
2
x , 2
1
ограничение имеет вид:
02112
21
xx , т. е. является активным (превращается в равенство),
но при этом число активных ограничений
1
l
меньше числа переменных
2
n
, а поэтому достаточные условия первого порядка не выполняются. Это
означает, что невозможно подтвердить или опровергнуть гипотезу о том, что

57
найденная точка — экстремум. Необходимо проверить выполнение доста-
точных условий второго порядка, связанных с анализом в рассматриваемой
точке знака второго дифференциала:
2
2
2
1
2
1
2
1
2
2
22
),(
),( dxdxdxdx
xx
xL
xLd
ji
i j
ji
с учётом выражений для первого дифференциала ограничений (в данном
случае — одного ограничения):
xx
i
i
i
j
i
n
i
i
j
j
dx
x
xq
dx
x
xq
dx
x
xq
dx
x
xq
xdq
2
2
1
1
1
1
2
11
)()(
)()(
)(
xx
dx
x
xx
dx
x
xx
2
2
21
1
1
21
)2()2(
011
2121
dxdxdxdx
x
x
,
откуда получается:
21
dxdx
.
Далее полученные значения подставляются во второй дифференциал
функции Лагранжа для определения его знака:
042)(222),(
2
2
2
2
2
2
2
2
2
1
2
dxdxdxdxdxxLd
,
который всегда положительный (как с рассмотренной ранее точке
T
x )0,0(
).
Так как в рассматриваемой точке 02
1
, то достаточное условие
максимума второго порядка не выполняется, поэтому сказать что-то опреде-
лённое о рассматриваемой точке невозможно. Остаётся проверить необходи-
мые условия второго порядка, которое сводится к анализу знака второго
дифференциала функции Лагранжа:
044),(
2
1
2
2
2
dxdxxLd
при любых
1
dx и
2
dx , т. е. необходимое условие второго порядка для макси-
мума не выполняется, следовательно, максимума точно нет.
Таким образом, получены следующие результаты:
1) в точке
T
x )0,0(
возможен условный минимум;
2) в точке
T
x )1,1(
нет ни минимума, ни максимума.
5. Далее в найденной точке экстремума следует найти значение целевой
функции:
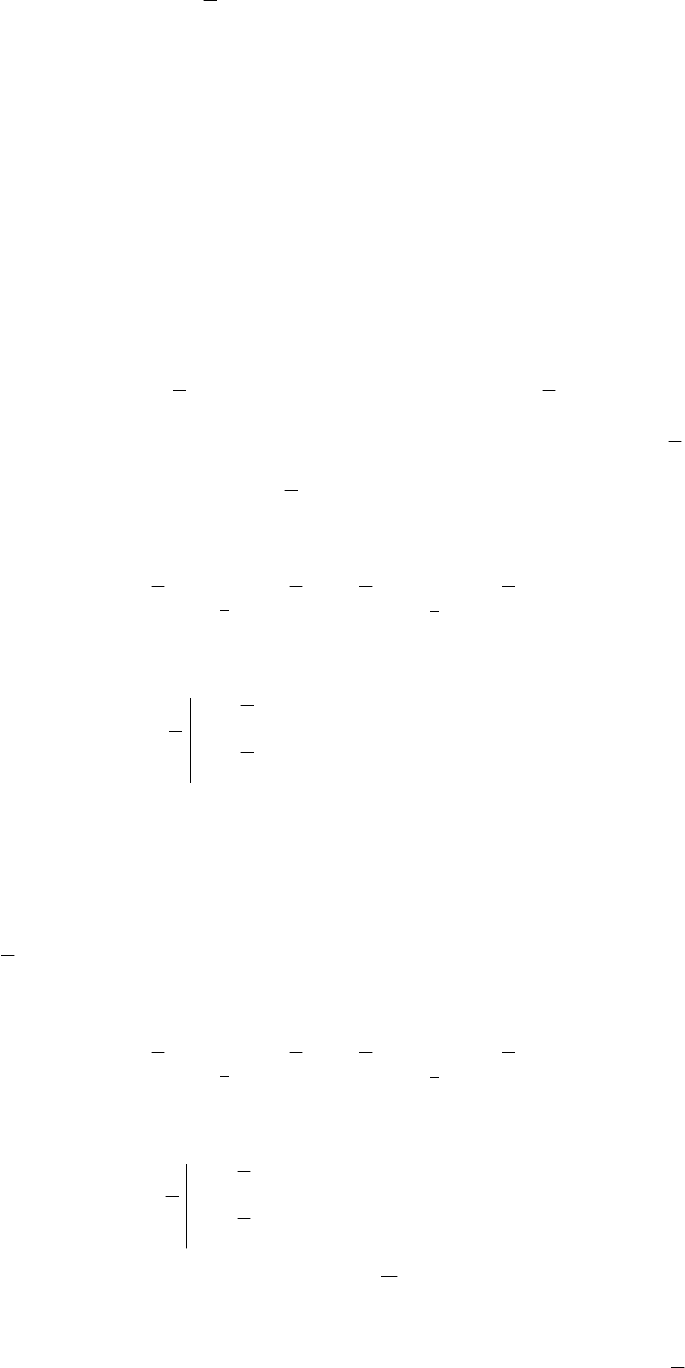
58
000)(
2
2
2
1
xxxI .
Таким образом, решаются задачи нахождения условного экстремума с
ограничениями-неравенствами.
2.3.4 Задача условной оптимизации со смешанными ограничениями
(равенствами и неравенствами)
Постановка задачи условной оптимизации со смешанными ограни-
чениями
Задача условной оптимизации со смешанными ограничениями фор-
мулируется следующим образом: даны дважды непрерывно дифференциру-
емые целевая функция
)
(
x
I
и функции ограничений
)
(
x
q
, определённые на
множестве
n
RX , требуется исследовать целевую функцию
)
(
x
I
на экс-
тремумы, т. е. определить точки
X
x
её минимумов и максимумов на
множестве
X
:
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных равенствами и неравенствами:
,,),1(,0)(
;;,,1,0)(
pmjxq
nmmjxq
xX
j
j
где
m
и
p
— целые числа.
Необходимые условия экстремума первого порядка в задаче со сме-
шанными ограничениями
Пусть
x
есть точка локального экстремума в задаче условной оптими-
зации
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных равенствами и неравенствами:
,,),1(,0)(
;;,,1,0)(
pmjxq
nmmjxq
xX
j
j
.
Тогда найдется число 0
0
и вектор
, не равные одновременно нулю
и такие, что выполняются следующие условия:
условие стационарности обобщённой функции Лагранжа по
x
:

59
0
),,(
0
i
x
xL
,
n
i
,
,
1
или в векторной форме (через градиент) 0),,(
0
xL
x
;
условие допустимости решения:
0)(
xq
j
,
m
j
,
,
1
;
0)(
xq
j
,
p
m
j
,
,
1
;
условие неотрицательности для условного минимума:
pmj
j
,...,1,0
или условие неположительности для условного максимума:
pmj
j
,...,1,0
;
условие дополняющей нежёсткости:
pmjxq
jj
,...,1,0)(
.
Если при этом градиенты активных в точке
x
ограничений-равенств и
ограничений-неравенств )(
1
xq
x
, )(
2
xq
x
, …, )(
xq
mx
, )(
1
xq
mx
, …,
)(
xq
px
линейно независимы (выполняется условие регулярности), то
0
0
.
Пояснения.
Условия знаокопределённости (неотрицательности и неположительно-
сти), а также условие дополняющей нежёсткости записывается только для
тех множителей Лагранжа, которые относятся к ограничениям-неравенствам.
Условие дополняющей нежёсткости понимается следующим образом:
чтоб было равно нулю произведение, нулю должен равняться хотя бы один
из сомножителей. Это означает, что если какое-то условие-неравенство пас-
сивное [ 0)(
xq
j
, т. е. не равно нулю], то соответствующий коэффициент
Лагранжа равен нулю 0
j
. Если же это условие-неравенство активное
[ 0)(
xq
j
, т. е. равно нулю], то соответствующий коэффициент Лагранжа
может и не быть равным нулю (а может и быть равным). При этом в случае
максимума записывают условие 0
j
, а случае минимума 0
j
.
60
Достаточные условия экстремума первого порядка в задаче услов-
ной оптимизации со смешанными ограничениями
Пусть имеется точка ),(
x , удовлетворяющая необходимым условиям
экстремума первого порядка (рассмотренным выше) при 0
0
, суммарное
число ограничений-равенств и активных ограничений-неравенств в точке
x
совпадает с числом
n
переменных (при этом условие регулярности выполня-
ется). Если 0
j
для всех
a
Jj
, то точка
x
— условный локальный ми-
нимум. Если 0
j
для всех
a
Jj
, то точка
x
— условный локальный
максимум.
Необходимые условия экстремума второго порядка в задаче услов-
ной оптимизации со смешанными ограничениями
Пусть
x
— регулярная точка экстремума в задаче условной оптимиза-
ции и имеется решение ),(
x , удовлетворяющее необходимым условиям
экстремума первого порядка. Тогда второй дифференциал классической
функции Лагранжа в точке ),(
x неотрицателен для минимума:
0),(
2
xLd
и неположителен для максимума:
0),(
2
xLd
для всех первых дифференциалов
n
R
x
d
таких, что
0)(
xdq
j
,
m
j
,
,
1
,
a
Jj
при 0
j
для минимума и 0
j
для максимума,
0)(
xdq
j
,
a
Jj
при 0
j
.
Достаточные условия экстремума второго порядка в задаче услов-
ной оптимизации со смешанными ограничениями
Пусть имеется точка ),(
x , удовлетворяющая необходимым условиям
экстремума первого порядка (рассмотренным выше) при 0
0
. Если в этой
точке второй дифференциал классической функции Лагранжа неотрицателен
для минимума:
0),(
2
xLd
и неположителен для максимума:
