Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.

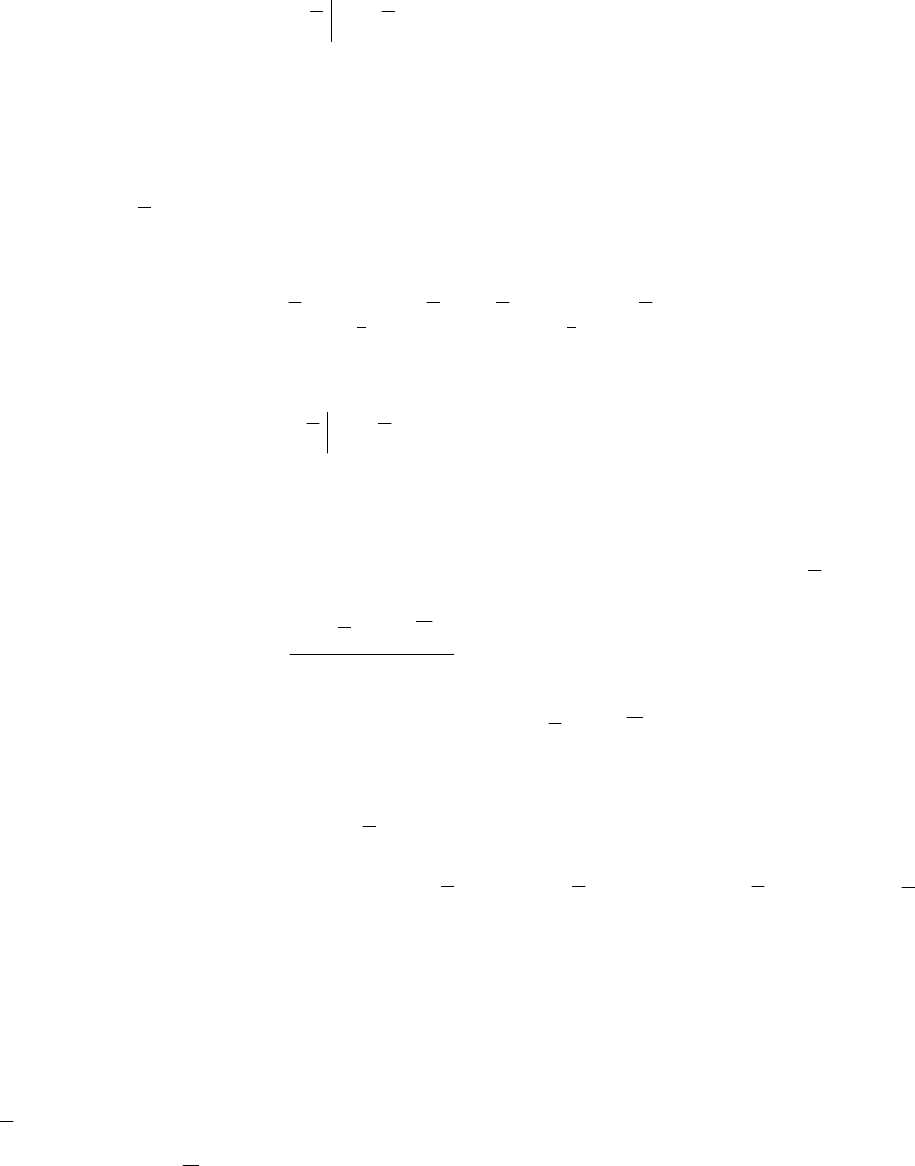
41
;;,,1,0)( nmmjxqxX
j
где
m
— целое число.
Необходимые условия экстремума первого порядка в задаче услов-
ной оптимизации с ограничениями-равенствами
Пусть
x
есть точка локального экстремума в задаче условной оптими-
зации
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных равенствами:
;;,,1,0)( nmmjxqxX
j
.
Тогда найдутся числа
0
,
1
, …
m
, не равные одновременно нулю и
такие, что выполняются следующие условия:
условие стационарности обобщённой функции Лагранжа по
x
:
0
),,(
0
i
x
xL
,
n
i
,
,
1
или в векторной форме (через градиент) 0),,(
0
xL
x
;
условие допустимости решения:
0)(
xq
j
,
m
j
,
,
1
.
Если при этом градиенты )(
1
xq
x
, )(
2
xq
x
, …, )(
xq
mx
в точке
x
линейно независимы, то 0
0
.
Пояснения.
Приведённые выше уравнения составляют вместе систему
m
n
урав-
нений с
1
m
n
неизвестными, в число которых входят
n
переменных
T
n
xxxx ),,,(
21
,
m
коэффициентов Лагранжа при функциях-
ограничениях
T
m
),,,(
21
и коэффициент Лагранжа при целевой
функции
0
. Так как число переменных в данном случае больше числа урав-
нений, то система имеет бесконечное число решений. Чтобы сделать решение
единственным, вместо обобщённой функции Лагранжа используют класси-
ческую функцию Лагранжа, для чего полученные выражения преобразуют
следующим образом. Принимают, что в общем случае 0
0
и делят уравне-
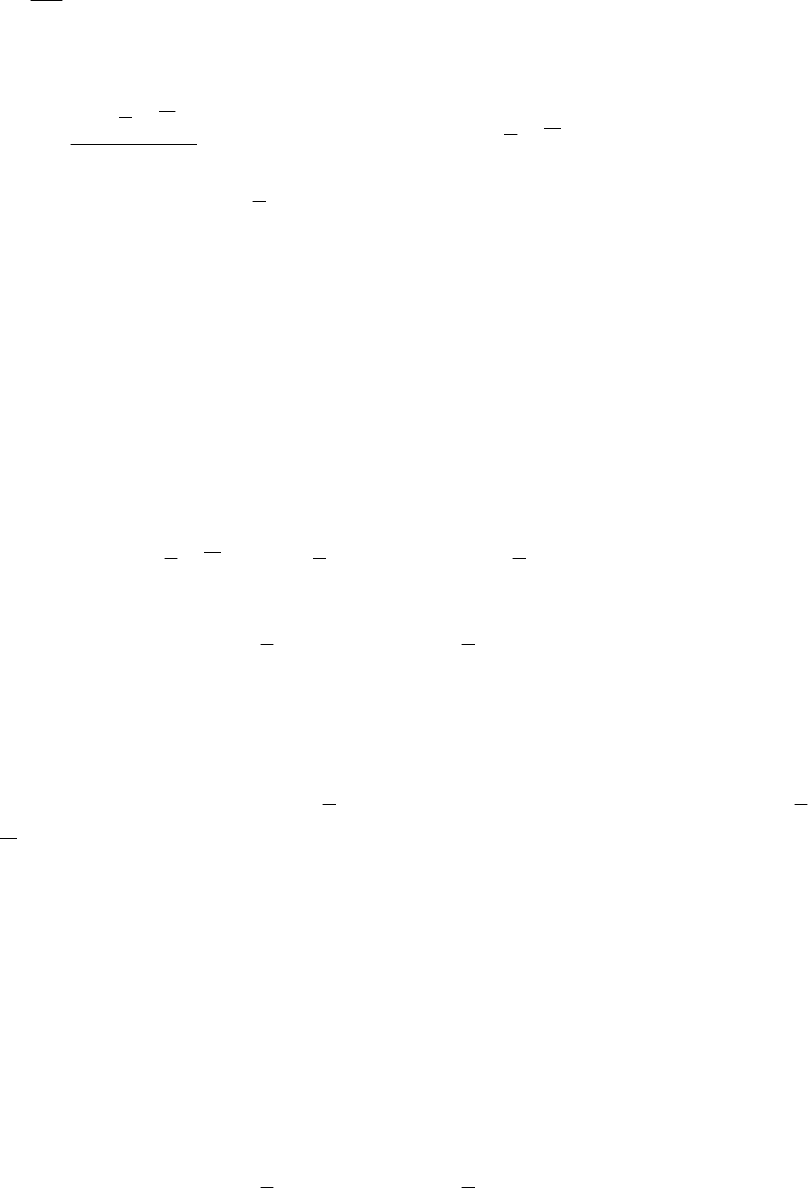
42
ния (градиент) функции Лагранжа на
0
, затем заменяют отношения коэф-
фициентов
0
j
на новые
j
. В результате функция Лагранжа становится
классической, а сама система уравнений приобретает вид:
0
),(
i
x
xL
,
n
i
,
,
1
или 0),(
xL
x
;
0)(
xq
j
,
m
j
,
,
1
,
где число уравнений становится равным числу переменных и в результате
система имеет единственное решение.
Полученные уравнения отражают тот факт, что антиградиент (градиент
со знаком минус) в точке экстремума равен линейной комбинации (сумме
слагаемых с коэффициентами) градиентов ограничений, что вытекает из сле-
дующих преобразований (с учётом разложения функции Лагранжа на состав-
ляющие — целевую функцию и линейную комбинацию ограничений):
0)()(),(
1
m
j
jjx
xqxIxL
;
m
j
jj
xqxI
1
)()(
.
Символ
x
при
L
в левой части первого выражения используется с ин-
дексом
x
, указывающим на то, что частные производные в этом градиенте
берутся по составляющим вектора
x
(функция Лагранжа зависит как от
x
,
так и от
). В правой части первого выражения индексы при
можно не
указывать, поскольку целевая функция и функции-ограничения зависят толь-
ко от
x
(и именно по
x
берутся их градиенты), поэтому путаницы, по каким
переменным берётся градиент, не будет.
Полученное выражение имеет следующий физический смысл. Градиент
в точке всегда является перпендикуляром к касательной в этой точке. В рас-
сматриваемой точке градиент целевой функции и результирующий градиент
функций-ограничений совпадают:
m
j
jj
xqxI
1
)()(
,
хотя имеют противоположные направления.

43
Т. е. движение вдоль одного градиента означает движение также вдоль
другого градиента. Можно провести аналогию с более простым случаем без-
условной оптимизации. Тогда имеется только градиент целевой функции и в
случае равенства нулю его направление совпадает с направлением оси изме-
нения целевой функции. Это означает наличие пика при максимуме или впа-
дины при минимуме (так как, например, при одном
x
в системе координат со
взаимно перпендикулярными осями, если касательная направлена вдоль оси
абсцисс, то перпендикуляр к касательной направлен вдоль оси ординат). Но
при условной оптимизации в рассмотрение вводится также результирующий
градиент функций-ограничений. Совпадение этих двух градиентов означает,
что они проходят через точку касания целевой функции и результирующей
функции ограничений (с учётом коэффициентов Лагранжа). Разнонаправлен-
ность градиентов означает, что при любом изменении независимых перемен-
ных
x
начнутся изменения целевой функции и функции ограничений, т. е.
точка, в которой градиенты равны, но направлены в противоположные сто-
роны, является единственной точкой стабильного положения.
Коэффициент
0
перед целевой функцией по своему физическому
смыслу не должен быть равен нулю ( 0
0
), полученная для этого случая
точка экстремума называется регулярной. Если принять 0
0
, то это озна-
чает исключение из рассмотрения целевой функции, т. е. вырожденность
(остаются только ограничения). Это фактически означает, что решаемая за-
дача перестаёт быть задачей оптимизации. Такая точка экстремума при
0
0
называется нерегулярной. Её можно было бы и не рассматривать, так
как она не соответствует корректно поставленной задаче оптимизации, но её
вводят для общности формальной постановки задачи.
Необходимые условия экстремума второго порядка в задаче услов-
ной оптимизации с ограничениями-равенствами
Пусть даны условия исходной оптимизационной задачи, а также соблю-
даются условие стационарности классической функции Лагранжа по
x
и
условие допустимости решения в форме:
,,,1,0)(
;,,1,0
),(
mjxq
ni
x
xL
j
i
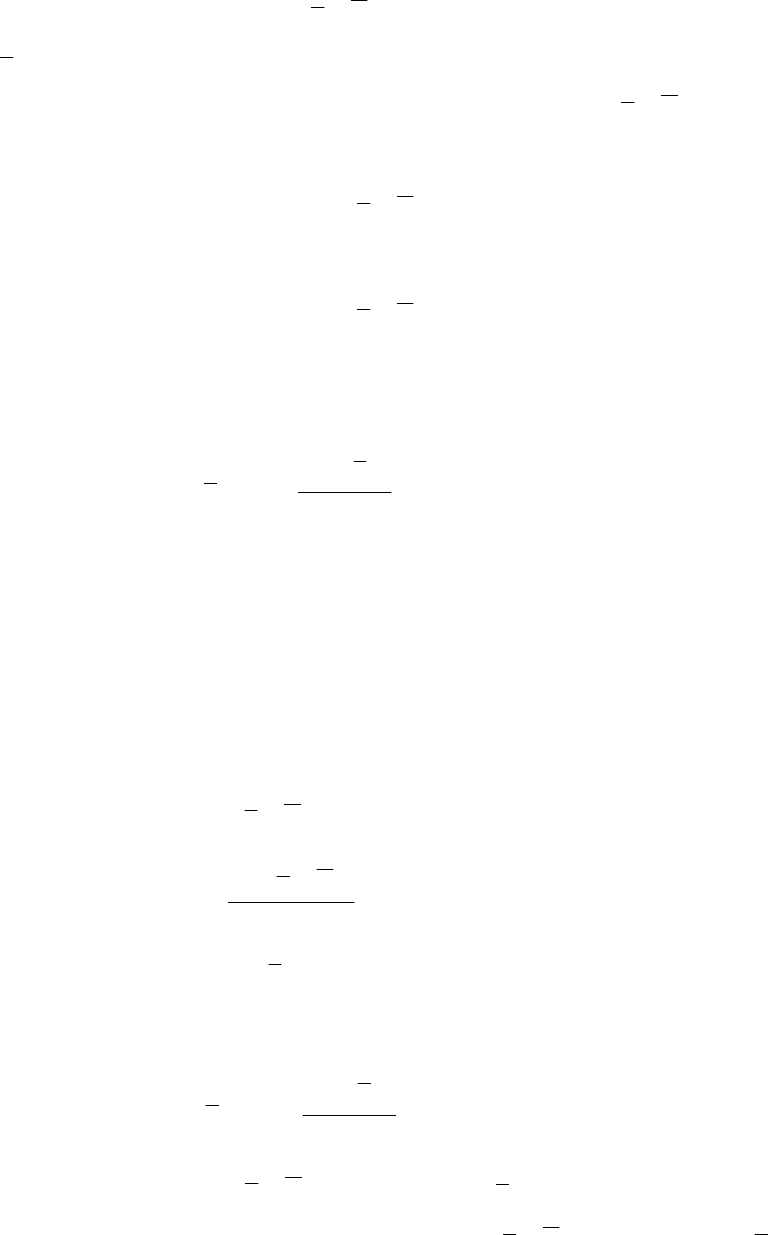
44
для которых имеется решение ),(
x , а соответствующая им точка экстре-
мума
x
является регулярной (т. е. задача невырожденная). Тогда второй
дифференциал классической функции Лагранжа в точке ),(
x неотрицате-
лен (для минимума)
0),(
2
xLd
или неположителен (для максимума)
0),(
2
xLd
для всех ненулевых
n
R
dx
таких, что первые дифференциалы функций-
ограничений
0
)(
)(
1
i
n
i
i
j
j
dx
x
xq
xdq ,
m
j
,
,
1
.
Последнее условие напоминает условие равенства нулю первых произ-
водных в задаче безусловной оптимизации, но там это условие было приме-
нено к производным целевой функции, а в данном случае — к функциям
ограничений.
Достаточные условия экстремума второго порядка в задаче услов-
ной оптимизации с ограничениями-равенствами
Пусть имеется точка ),(
x , удовлетворяющая системе
.,,1,0)(
;,,1,0
),(
mjxq
ni
x
xL
j
i
Если в этой точке для всех ненулевых
n
R
dx
таких, что
0
)(
)(
1
i
n
i
i
j
j
dx
x
xq
xdq ,
m
j
,
,
1
,
выполняется условие 0),(
2
xLd , то точка
x
является точкой локально-
го минимума, а если выполняется условие 0),(
2
xLd , то точка
x
явля-
ется точкой локального максимума.
Эти условия также аналогичны условиям существования экстремума в
задаче безусловной оптимизации (там речь идёт о вторых производных), но в
данном случае они дополнены условиями для функций ограничений.

45
Процедура нахождения экстремума в задаче условной оптимизации
включает ряд этапов, а поэтому может быть представлена в виде соответ-
ствующего алгоритма.
Алгоритм решения задачи условной оптимизации при ограничени-
ях-равенствах
Исходные данные: вектор искомых переменных
x
размерности
n
, целе-
вая функция
)
(
x
I
и функции-ограничения в форме равенств 0)(
xq
j
,
m
j
,
,
1
,
n
m
.
Шаг 1. Составляется обобщённая функция Лагранжа
p
j
jj
xqxIxL
1
00
)()(),,(
.
Шаг 2. Записываются необходимые условия экстремума первого поряд-
ка:
.,,1,0)(
;,,1,0
),,(
0
mjxq
ni
x
xL
j
i
Шаг 3. Решается полученная система уравнений для двух случаев:
1) 0
0
;
2) 0
0
, для чего первое условие шага 2 делится на
0
и производится
замена переменных
0
j
на новые
j
.
В результате находятся значения
x
и
, соответствующие стационар-
ным точкам
x
, которых в общем случае может быть несколько. Из них вы-
деляются те, что найдены при условии 0
0
— эти точки могут быть регу-
лярными точками экстремума.
Шаг 4. Для выделенных на шаге 3 точек проверяются достаточные
условия экстремума следующим образом:
а) записывается выражение для второго дифференциала классической
функции Лагранжа в точке ),(
x :
ji
n
i
n
j
ji
dxdx
xx
xL
xLd
1 1
2
2
),(
),(
;

46
б) записывается система уравнений для первого дифференциала функ-
ций ограничений:
0
)(
)(
1
i
n
i
i
j
j
dx
x
xq
xdq ,
m
j
,
,
1
;
в) из предыдущей системы выражаются любые
m
дифференциалов
i
dx
(по числу функций ограничений) через остальные
)
(
m
n
и подставляются
во второй дифференциал ),(
2
xLd ;
г) осуществляется проверка знака второго дифференциала: если
0),(
2
xLd при ненулевых
i
dx , то в точке
x
— условный локальный
минимум; если 0),(
2
xLd при ненулевых
i
dx , то в точке
x
— услов-
ный локальный максимум.
Если достаточные условия экстремума не выполняются, то следует про-
верить выполнение необходимых условий второго порядка по аналогичной
процедуре. Если они выполняются, то требуются дополнительные исследо-
вания, если не выполняются — в точке
x
нет условного экстремума.
Шаг 5. Если точки условного экстремума найдены, вычисляются значе-
ния в них целевой функции.
Пример 3.6. Пусть задана целевая функция
2
2
2
1
)( xxxI на множестве
02
21
xxxX , т. е. задано одно ограничение-равенство
02)(
211
xxxq , причём здесь
2
n
,
1
m
,
1
p
.
Чтобы решить, можно ли пользоваться классической функцией Лагран-
жа, проверяют условие регулярности, для чего определяют градиент функции
ограничения:
0
1
1
)2(
)2(
)(
)(
)(
1
21
1
21
1
1
x
xx
x
xx
x
xq
x
xq
xq .
Поскольку градиент не равен нулю, то условие регулярности выполня-
ется, т. е. все векторы градиента линейно независимы. Линейная независи-
мость означает, что нет двух векторов, различающихся между собой на по-
стоянный коэффициент. Поэтому можно пользоваться классической функци-
ей Лагранжа (при 1
0
).
1. Составляется классическая функция Лагранжа:
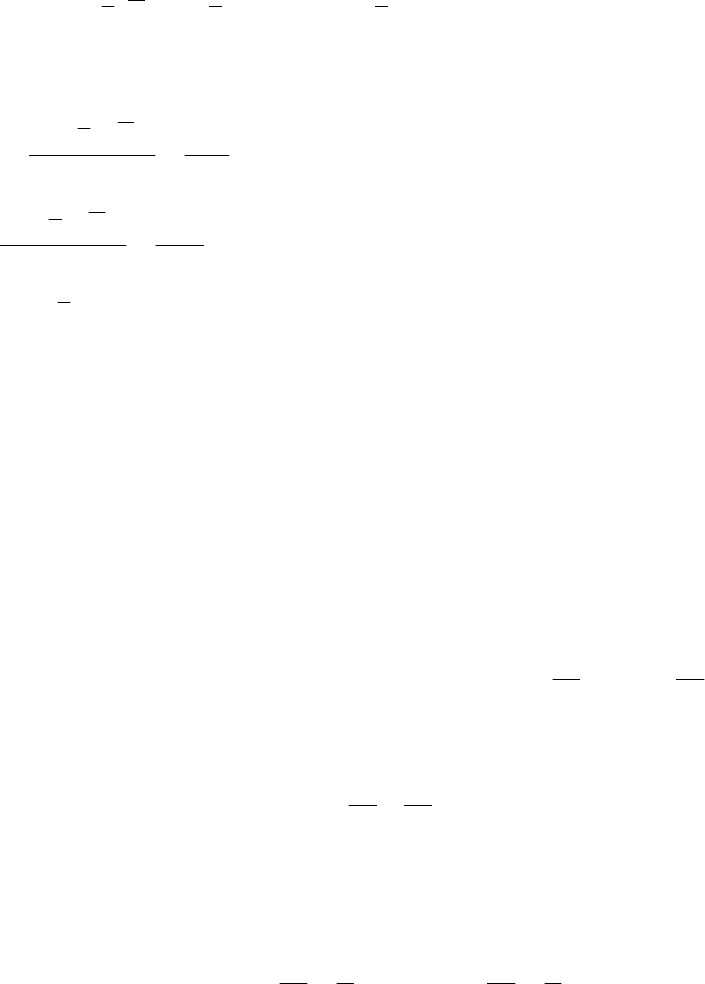
47
)2()()()(),(
211
2
2
2
1
1
1
xxxxxqxIxL
j
jj
.
2. Выписываются необходимые условия экстремума первого порядка:
а)
022
),(
11211
2
2
2
1
11
xxxxx
xx
xL
,
022
),(
12211
2
2
2
1
22
xxxxx
xx
xL
;
б) 02)(
21
xxxq .
Таким образом, получена система уравнений:
,02
;02
;02
21
12
11
xx
x
x
для которой ищется решение.
3. Решение системы может быть получено различным образом, в частно-
сти:
а) из первых двух уравнений получают:
2
1
1
x ,
2
1
2
x ;
б) подставляют их в третье уравнение:
022
2
2
2
1
11
21
xx ,
откуда 2
1
;
в) полученное значение подставляется:
1
2
2
2
1
1
x , 1
2
2
2
1
2
x ,
таким образом, найдено решение: 2
1
, 1
1
x , 1
2
x ; это — условно-
стационарная точка (стационарная для условной оптимизации). Эта точка
может быть экстремумом (а может и не быть, так как получена из необходи-
мых условий).
4. Чтобы подтвердить, что найденная точка действительно является экс-
тремумом, и определить его вид (максимум или минимум), проверяются до-
статочные условия экстремума второго порядка:
а) записывается второй дифференциал функции Лагранжа:
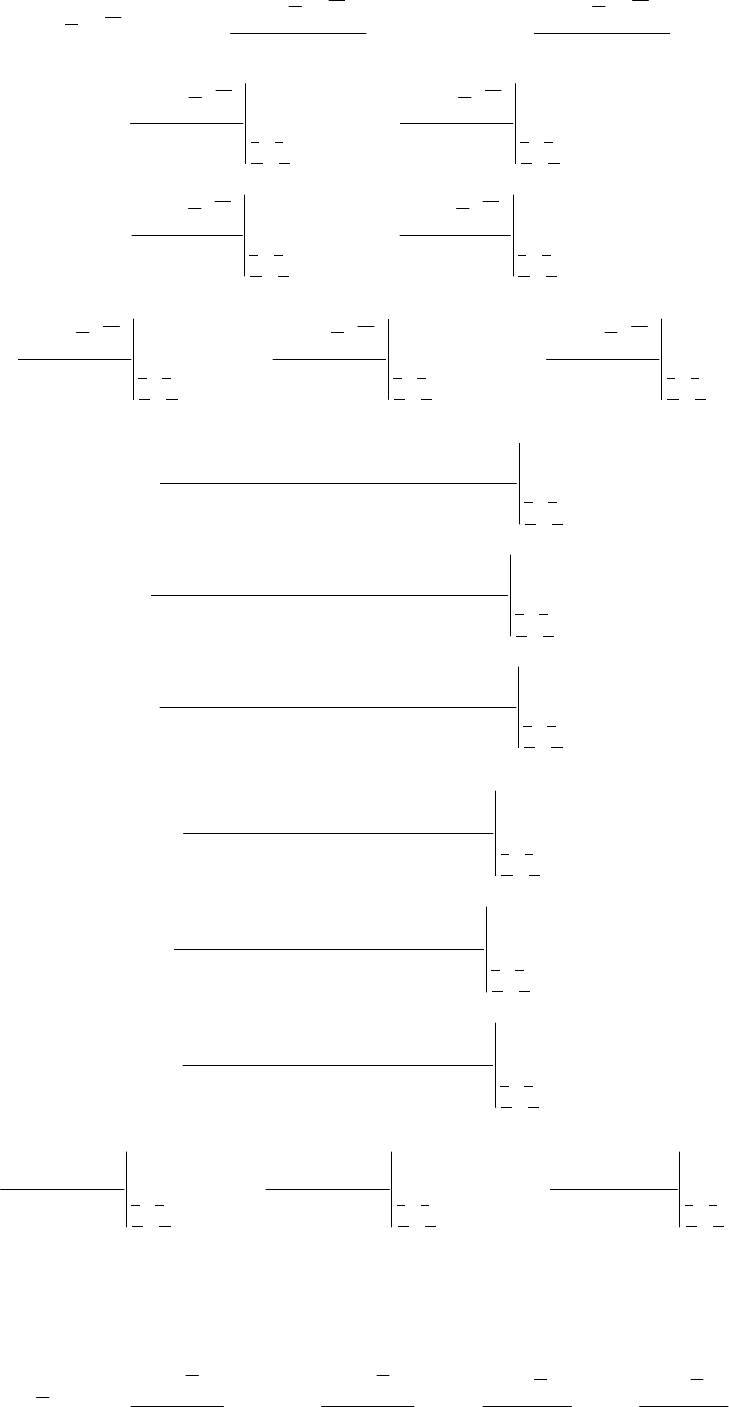
48
ji
i j
ji
ji
n
i
n
j
ji
dxdx
xx
xL
dxdx
xx
xL
xLd
2
1
2
1
2
1 1
2
2
),(),(
),(
21
21
2
11
11
2
),(),(
dxdx
xx
xL
dxdx
xx
xL
xxxx
22
22
2
12
12
2
),(),(
dxdx
xx
xL
dxdx
xx
xL
xxxx
2
2
2
2
2
21
21
2
2
1
2
1
2
),(),(
2
),(
dx
x
xL
dxdx
xx
xL
dx
x
xL
xx
xx
xx
2
1
2
1
211
2
2
2
1
2
)]2()[(
dx
x
xxxx
xx
21
21
211
2
2
2
1
2
)]2()[(
2 dxdx
xx
xxxx
xx
2
2
2
2
211
2
2
2
1
2
)]2()[(
dx
x
xxxx
xx
2
1
1
1
1
)]001()02[(
dx
x
x
xx
21
2
1
1
)]001()02[(
2 dxdx
x
x
xx
2
2
2
1
2
)]010()20[(
dx
x
x
xx
2
2
2
12
21
2
11
2
1
1
11
]2[]2[
2
]2[
dx
x
x
dxdx
x
x
dx
x
x
xxxxxx
2
2
2
1
2
221
2
1
222)0(22 dxdxdxdxdxdx .
б) записывается первый дифференциал ограничения:
2
2
1
1
1
1
2
11
)()(
)()(
)( dx
x
xq
dx
x
xq
dx
x
xq
dx
x
xq
xdq
i
i
i
j
n
i
i
i
j
j
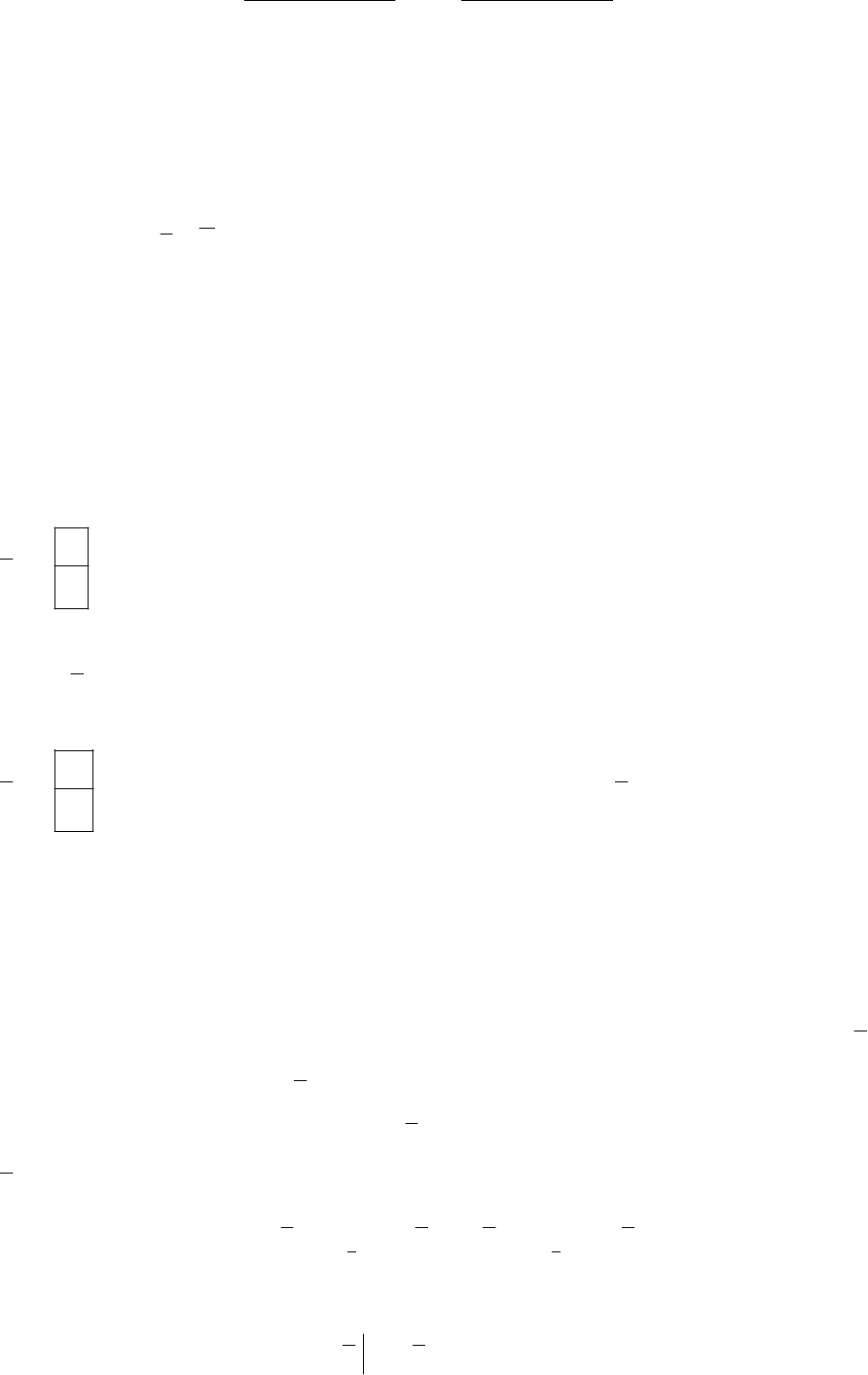
49
2
2
21
1
1
21
)2()2(
dx
x
xx
dx
x
xx
0)010()001(
2121
dxdxdxdx .
в) из последнего уравнения получают:
21
dxdx
;
г) последнее выражение подставляется во второй дифференциал функ-
ции Лагранжа:
042))((222),(
2
2
2
222
2
2
2
1
2
dxdxdxdxdxdxxLd
,
если 0
2
dx , так как квадрат любой переменной (в том числе дифференциа-
ла) всегда положительный, а условие 0
2
dx является необходимым в связи
с тем, что в противном случае невозможно брать первую производную по
2
dx (это же относится и к дифференциалу
1
dx ).
Поэтому в найденной точке 1
1
x , 1
2
x — регулярный локальный
условный минимум. Иначе решение можно запись в виде вектора
T
x )1,1(
1
1
.
5. Вычисляется значение целевой функции в найденной точке экстрему-
ма: 2)1()1()(
222
2
2
1
xxxI . При решении задачи на безусловный экс-
тремум для той же целевой функции было найдено решение
T
x )0,0(
0
0
. Видно, что введение условия 02)(
211
xxxq суще-
ственно изменило решение.
2.3.3 Задача условной оптимизации с ограничениями-неравенствами
Постановка задачи условной оптимизации с ограничениями-
неравенствами
Даны дважды непрерывно дифференцируемые целевая функция
)
(
x
I
и
функции ограничений
)
(
x
q
, определённые на множестве
n
RX , требуется
исследовать целевую функцию
)
(
x
I
на экстремумы, т. е. определить точки
X
x
её минимумов и максимумов на
X
:
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных равенствами:
,,,1,0)( mjxqxX
j
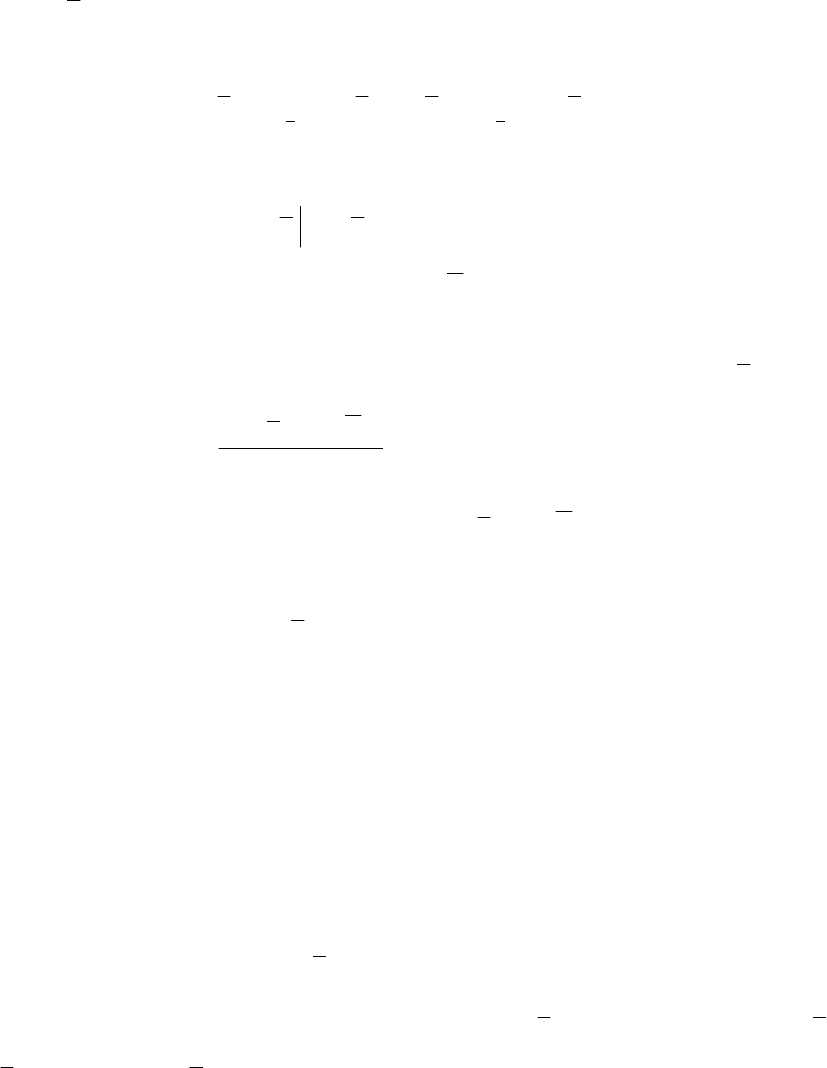
50
где
m
— целое число.
Необходимые условия экстремума первого порядка в задаче услов-
ной оптимизации с ограничениями-неравенствами
Пусть
x
есть точка локального экстремума в задаче условной оптими-
зации
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных неравенствами:
.,,1,0)( mjxqxX
j
.
Тогда найдется число 0
0
и вектор
, не равные одновременно нулю
и такие, что выполняются следующие условия:
условие стационарности обобщённой функции Лагранжа по
x
:
0
),,(
0
i
x
xL
,
n
i
,
,
1
или в векторной форме (через градиент) 0),,(
0
xL
x
;
условие допустимости решения:
0)(
xq
j
,
m
j
,
,
1
;
условие неотрицательности для условного минимума:
mj
j
,...,1,0
или условие неположительности для условного максимума:
mj
j
,...,1,0
;
условие дополняющей нежёсткости:
mjxq
jj
,...,1,0)(
.
Если при этом градиенты активных в точке
x
ограничений )(
1
xq
x
,
)(
2
xq
x
, …, )(
xq
mx
линейно независимы (выполняется условие регу-
лярности), то 0
0
.
