Бронов С.А. Методы оптимизации в САПР

Подождите немного. Документ загружается.

111

Это произошло вследствие использование при выкладках алгоритма

Гаусса-Жордана. Смысл этого в том, что полученное решение можно пред-

ставить в виде матрицы:

2/1

2/5

2/3

1000

0100

0010

0001



откуда и определяются все базисные переменные, а все небазисные равны

нулю (так как небазисные): 0



s , 0



s .

Итак, решение получено — найдены оптимальные значения, которые

можно интерпретировать, например, следующим образом:

следует производить 3 единицы продукции

x ;

одновременно следует производить 1,5 единицы продукции

x ;

тогда доход составит 21 денежную единицу.

Впрочем, интерпретация задачи зависит от её исходной постановки.

Из результирующей симплекс-таблицы можно извлечь также дополни-

тельную информацию. Дополнительные переменные при оптимальном ре-

шении имеют значения: 0



s , 0



s , 5,2



s , 5,0



s . Это означает (по

физическому смыслу дополнительных переменных), что необходимые ресур-

сы

s и

s используются полностью, а ресурсы

s и

s имеют избыток, соот-

ветственно, 5,1



s единиц (в которых измеряется ресурс

s ) и 5,0



s еди-

ниц (в которых измеряется ресурс

s ). Такая интерпретация связана с тем,

что дополнительная переменная

s вводилась в первое ограничение (по ре-

сурсу 1), дополнительная переменная

s вводилась во второе ограничение

(по ресурсу 2), дополнительная переменная

s вводилась в третье ограниче-

ние (по ресурсу 3), дополнительная переменная

s вводилась в четвёртое

ограничение (по ресурсу 4). Что это за ресурсы — определяется постановкой

задачи, но во всех задачах ЛП это — всегда какие-либо ресурсы: по издерж-

кам, используемым компонентам, времени, расстоянию и т. д.

Анализ ресурсов позволяет принимать управленческие решения. Если

нас устраивает получаемый доход, то следует уменьшить запасы тех ресур-

сов, которые избыточны (

s и

s ), до нуля. Это позволит сэкономить на из-

держках по их приобретению, хранению и т. п. Если желательно увеличить

доход, то следует попробовать увеличить те ресурсы, которые оказались

112

полностью использованы (

s и

s ). Например, это может быть площадь

складов, число работников, выделяемое время и т. д.

В данной постановке не решается задача отыскания объёма ресурсов,

которые необходимы для получения некоторого заданного дохода — такую

задачу можно решить, но в другой постановке. Здесь же определяется макси-

мально возможный вариант (для задачи максимизации) или минимально воз-

можный вариант (для задачи минимизации) в имеющихся ограничениях по

ресурсам. Одновременно выявляется степень использования ресурсов и воз-

можность их уменьшения без вреда для полученного решения.

5.4 Двойственность задачи линейного программирования и

её использование

Задача линейного программирования в рассмотренной выше форме

называется прямой задачей линейного программирования. В линейном про-

граммировании существует понятие двойственной задачи, в которой меняют-

ся местами переменные и ограничения.

Пусть задача ЛП задана в симметрической первой форме:

 целевая функция:

 

max

2211







iinn

xcxcxcxcxI  ;

 ограничения:

















mmnnmmm

ybxaxaxa

;

,22,11,

22,222,211,2

11,122,111,1







 неотрицательность всех переменных:





0,,,





xxxx



т. е. когда целевая функция максимизируется, а все ограничения — типа

"меньше или равно".

Этой задаче можно сопоставить другую задачу следующего вида:

 целевая функция:

 

min

2211







iinn

ybybybybyF  ;

 ограничения:

113

















;

,2,21,1

22,22,212,1

1,122,111,1

nmnmnn

cyayaya



 неотрицательность всех переменных:





0,,,





yyyy



т. е. теперь целевая функция минимизируется, а все ограничения — типа

"больше или равно".

Полученная задача является двойственной по отношению к исходной (а

исходная является двойственной по отношению к полученной). Т. е. всегда

имеются пары взаимодвойственных задач ЛП: прямая (исходная) и двой-

ственная.

Если исходная задача задана в симметрической второй форме, то все

знаки неравенств (в целевых функциях и ограничениях) меняются на проти-

воположные.

Решают двойственные задачи точно так же, как и прямые. Иногда по-

становка задачи сама диктует, какая задача должна считаться прямой, но

иногда прямой может оказаться любая из двух возможных задач и тогда

двойственная появляется после рассмотренных формальных преобразований.

Между взаимодвойственными задачами имеются следующие соотноше-

ния:

1) если основная задача — на максимум (минимум) с системой ограни-

чений типа "меньше или равно" ("больше или равно"), то двойственная зада-

ча должна быть на минимум (максимум) с ограничениями типа "больше или

равно" ("меньше или равно");

2) в основной задаче все переменные должны быть неотрицательными

(если это не так, необходимо её преобразовать соответствующим образом,

как это рассмотрено выше);

3) коэффициентами целевой функции двойственной задачи являются

свободные члены системы ограничений основной задачи, и их число равно

;

4) матрица системы ограничений двойственной задачи получается

транспонированием матрицы системы ограничений основной задачи;

5) свободными членами системы ограничений двойственной задачи яв-

ляются коэффициенты целевой функции основной задачи, и их число равно

;

6) все переменные двойственной задачи неотрицательны.

114

Таким образом, двойственная задача является зеркальным отражением

основной задачи.

Свойство двойственности позволяет упростить решение некоторых за-

дач. Например, если в задаче 10 переменных и 2 ограничения, то можно пре-

образовать её к задаче, в которой 2 переменные и 10 ограничений.

Взаимодвойственные задачи при совместном применении позволяют

разрабатывать более эффективные алгоритмы и давать оценки возможным

решениям. При этом существует некоторое количество теорем, касающихся

различные сторон решения задач ЛП.

Теорема 1. Если одна из пары взаимодвойственных задач линейного

программирования имеет решение, то и другая задача имеет решение, и при

этом значения целевых функций этих задач одинаковы: )()(

optopt

yFxI



Теорема 2. Произвольное допустимое базисное решение задачи линей-

ного программирования оптимально тогда и только тогда, когда система

ограничений двойственной задачи совместна.

Теорема 3. Если целевая функция задачи линейного программирования

не ограничена снизу (или сверху), то система ограничений двойственной за-

дачи несовместна.

5.5 Решение задачи линейного программирования с исполь-

зованием программных средств

5.5.1 Решение задачи линейного программирования с помощью про-

граммы Excel

Задача ЛП представляет собой систему линейных уравнений (для целе-

вой функции и ограничений) и всегда может быть представлена в матричном

виде. Поэтому её удобно решать с использованием электронных таблиц

Excel. При этом можно написать свои команды обработки исходных данных,

но в Excel уже заложена возможность решения задачи ЛП с помощью специ-

альных встроенных средств. Ниже рассматривается решение задачи ЛП с ис-

пользованием Excel2003, но аналогично задача решается также в Excel2007.

Пусть имеется задача ЛП в следующем виде:

целевая функция: max45)(







xxxI ,

ограничения:

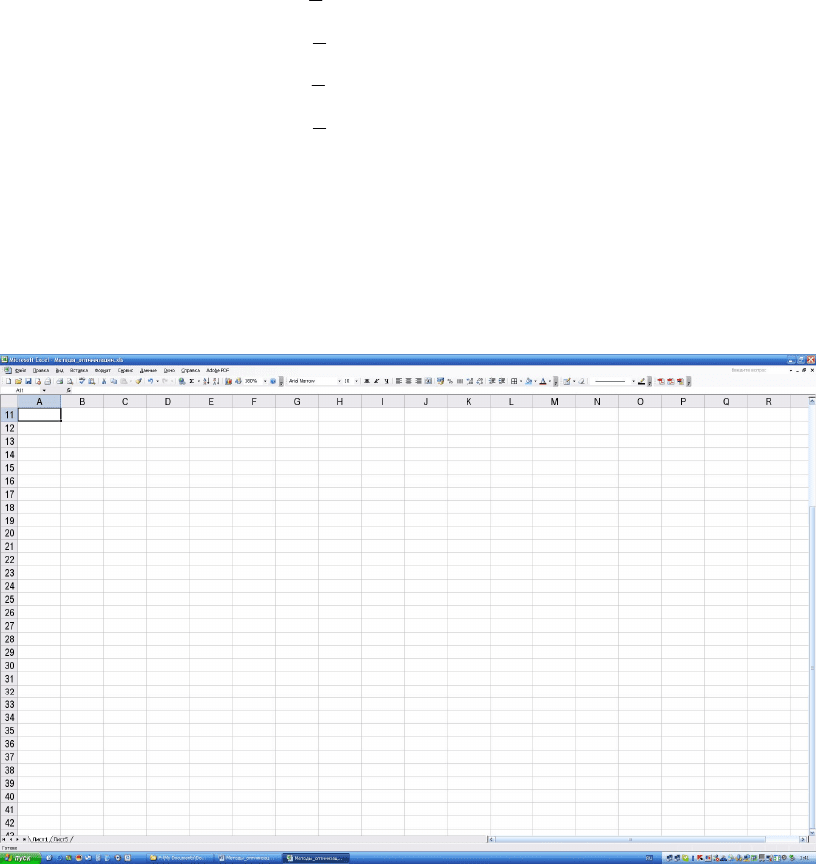
115



















.0,

;2)(

;1)(

;62)(

;2446)(

213

212

211

xxq

xxxq

Для решения этой задачи можно использовать Excel2003.

Для этого выполняются следующие действия.

Вызывается Excel2003 (Рисунок 5.7).

Рисунок 5.7 — Вызов программы Excel2003

Далее следует подготовить таблицы данных с коэффициентами для це-

левой функции и ограничений, а затем — вызвать специальные встроенные

средства Excel. Наряду с коэффициентами вводятся и поясняющие надписи

(Рисунок 5.8).

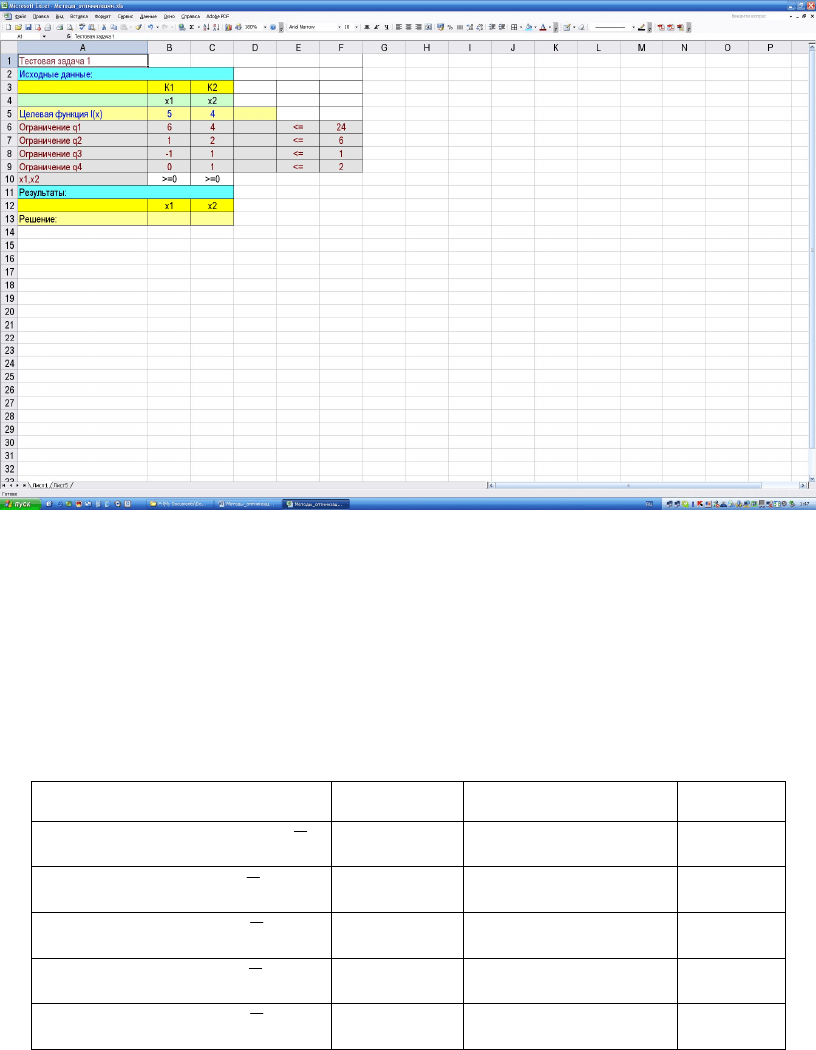
116

Рисунок 5.8 — Ввод таблицы данных

Далее в ячейки с D5 по D9 вводятся формулы, соответствующие уравне-

ниям целевой функции и ограничений:

2211

xbxb



, где

— коэффициенты

перед переменными в целевой функции и ограничениях.

Таблица 5.6 — Формулы для ячеек таблицы

Формула

Формула Excel Ячейка

Целевая функция

)

(

45 xx



=B5*B$13:C5*C$13

Ограничение )(

46 xx



=B6*B$13:C6*C$13

Ограничение )(

2xx



=B7*B$13:C7*C$13

Ограничение )(





=B8*B$13:C8*C$13

Ограничение )(

=B9*B$13:C9*C$13

Для ввода формул достаточно набрать одну из них (например, для ячей-

ки D5), затем скопировать её в остальные ячейки. В результате в соответ-

ствующих ячейках появятся нули (Рисунок 5.9).

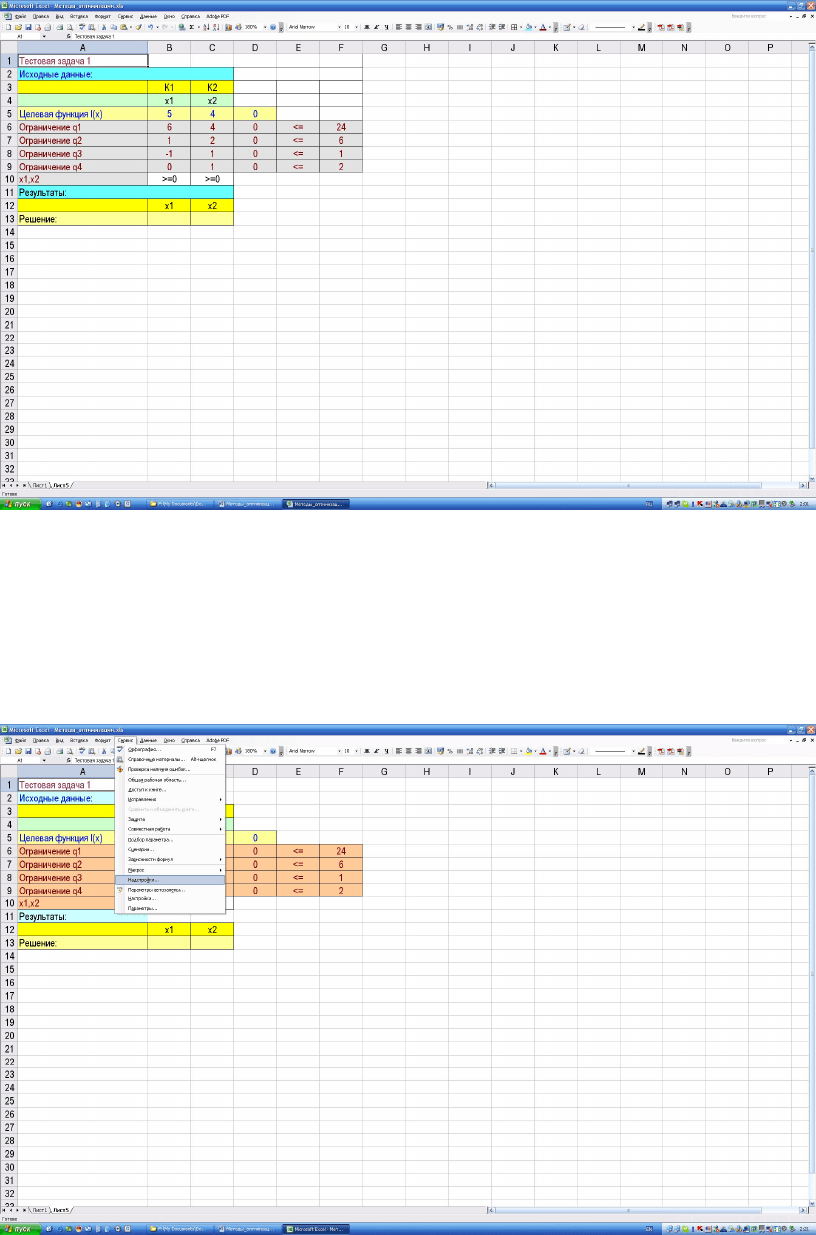
117

Рисунок 5.9 — После ввода формул с ячейки D5:D9

Затем вызывается специальная надстройка для организации поиска ре-

шения задачи ЛП. Для этого открывается меню Сервис и в нём выбирается

команда Надстройки… (Рисунок 5.10).

Рисунок 5.10 — Подготовка встроенных средств решения задачи ЛП

Появляется вкладка (Рисунок 5.11), в которой выбирается команда Поиск

решения.

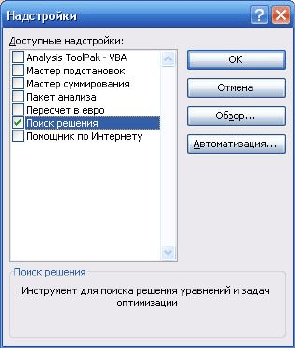
118

Рисунок 5.11 — Вкладка для выбора встроенных средств

решения задачи ЛП: Поиск решения

Далее вновь выбирается меню Сервис, в котором теперь уже имеется

команда Поиск решения, которая и выбирается, в результате появляется соот-

ветствующая вкладка (Рисунок 5.13). В полях этой вкладки размещается ин-

формация о подготовленной таблице.

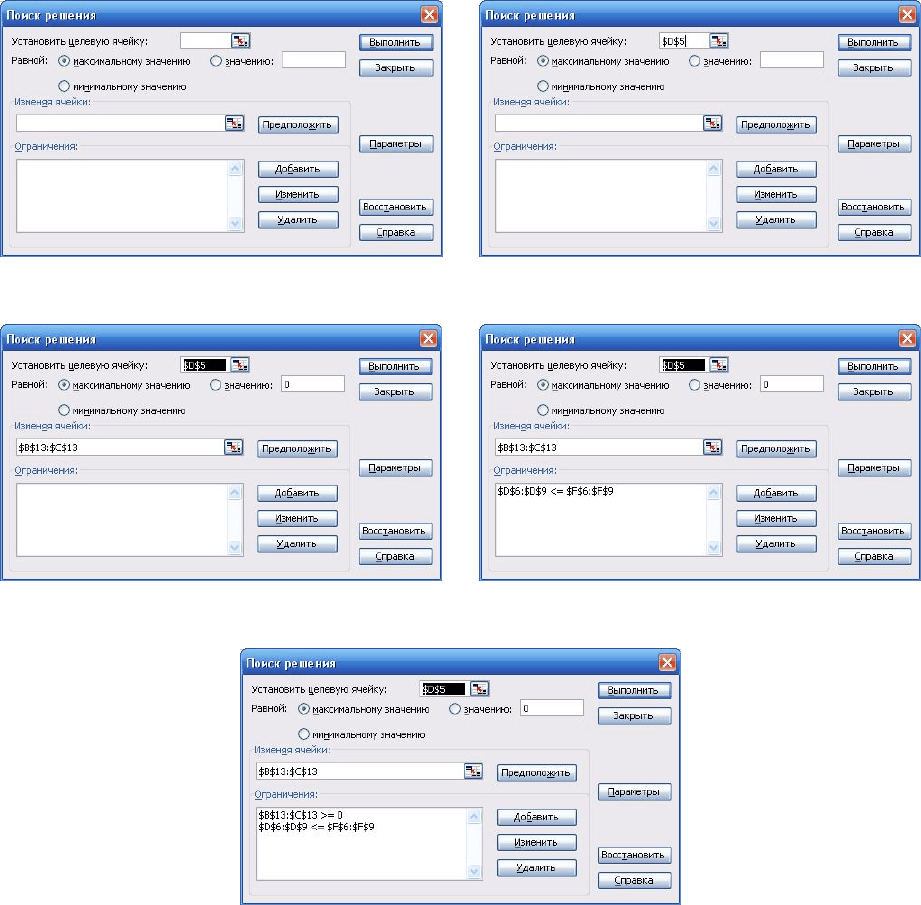
В поле Установить целевую ячейку помещают адрес ячейки со значением

целевой функции, для чего вначале помещают курсор в это поле, а затем —

перемещают на ячейку D5, которая предназначена для хранения результата

вычисления целевой функции. Адрес ячейки в данном случае представляется

в форме $D$5 (где знак доллара символизирует, что адрес для строк и столб-

цов ячейки является абсолютным в смысле программы Excel). Далее помеча-

ется поле Равной:  максимальное значение, а в правом поле от слова значению:

не ставиться ничего. Далее курсор помещается в поле Изменяя ячейки:, в кото-

рых будут указаны адреса ячеек со значениями переменных

, которые

должны варьироваться, в данном случае это ячейки B5:C5. Можно также по-

пробовать нажать клавишу вкладки Предположить, тогда Excel попробует сам

догадаться, в каких ячейках располагаются варьируемые переменные

. При

стандартном расположении таблицы, скорее всего, будет получен правиль-

ный результат. В данном случае вводится диапазон ячеек в виде абсолютных

адресов: $B$5:$C$5. Далее следует ввести диапазон адресов ячеек для ограни-

чений, для чего нажимается клавиша вкладки Добавить.

119

а) б)

в)

г) д)

Рисунок 5.12 — Вкладка для ввода диапазона ячеек с ограничениями

В поле Ссылка на ячейку записывается диапазон адресов, в данном случае

это $D$6:$D$9 (вводится, как обычно в Excel, указанием курсора на первую и

последнюю ячейку с удержанием клавиши Shift). В поле справа выбирается

тип неравенства (в данном случае <=, что соответствует нестрогое неравен-

ство типа "меньше или равно"). В крайнем правом поле помещается ссылка

на диапазон ячеек, в которых указаны значения ограничений: в данном слу-

чае это ячейки $F$6: $F$9 (в которых расположены числа 24, 6, 1, 2). После

нажатия клавиши меню OK эта информация вводится в большое поле вклад-

ки. Далее следует указать ограничения, связанные с неотрицательностью пе-

ременных

. Для этого на вкладке нажимается клавиша Добавить и вводится

диапазон ячеек, в которых будут получаться решения

, в данном случае это

ячейки в диапазоне $B$13:$C$13. В поле справа следует выбрать знак => , а в

крайнем правом поле поставить число.

120

а) б)

в) г)

д)

Рисунок 5.13 — Вкладка для настройки встроенных средств

решения задачи ЛП

Настройка завершена. Далее нажимается клавиша вкладки Выполнить и

Excel ищет решение задачи ЛП.