Бронов С.А. Методы оптимизации в САПР

Подождите немного. Документ загружается.

 

iikk

bxaxq 

















pmmmk





,...,2,1 ,

системы ограничений типа неравенств "меньше или равно":

 

iikk

bxaxq 

















spmpmpmk





,...,2,1 ,

где

— весовые коэффициенты ограничений (действительные числа).

Смысл приведённых выражений заключается в следующем.

Имеется

переменных

x ,

x , …,

x , образующих линейную целевую

функцию, а также

ограничений типа равенства,

ограничений типа нера-

венства "больше или равно" и

ограничений типа неравенства "меньше или

равно". Все функции (целевая и ограничения) линейны, т. е. представляют

собой сумму указанных переменных

x ,

x , …,

x , умноженных на весовые

коэффициенты (вещественные числа с любым знаком).

В развёрнутом виде ограничения типа равенства представляются следу-

ющим образом:





 













;

,22,11,

2,222,211,22

1,122,111,11

mnnmmmm

bxaxaxaxq



ограничения типа неравенства "меньше или равно":





 















;

,22,11,

2,222,211,22

1,122,111,11

pmnnpmpmpmpm

mnnmmmm

bxaxaxaxq



ограничения типа неравенства "больше или равно":





 















;

,22,11,

2,222,211,22

1,122,111,11

spmnnspmspmspmspm

pmnnpmpmpmpm

bxaxaxaxq



Таким образом, с формальной точки зрения имеется обычная задача оп-

тимизации с линейной целевой функцией и линейными ограничениями сме-

шанного типа (в виде равенств и неравенств — "больше или равно" и "мень-

ше или равно"). Именно поэтому задача называется задачей линейного про-

граммирования. Если бы целевая функция или какие-то ограничения были

нелинейными, то мы получили бы задачу нелинейного программирования.

Все оптимизационные задачи, которые не имеют аналитического реше-

ния (линейные и нелинейные), решаются численными итерационными мето-

дами. Последовательность решения заключается в том, что задаются произ-

вольные наборы значений переменных

xxxx ),,,(



 и вычисляются со-

ответствующие им значения целевой функции, которые сравниваются между

собой. В качестве экстремума принимается то значение

xxxx ),,,(



 ,

при котором обеспечивается максимальное (при максимизации) или мини-

мальное (при минимизации) значение целевой функции. В общем случае

необходимо перебрать все возможные сочетания переменных

x ,

x , …,

x ,

которых — бесконечное множество. Чтобы уменьшить область поиска экс-

тремума, выделяют область допустимых решений (ОДР), для чего исполь-

зуют ограничения. В рассмотренном примере каждое новое ограничение

представляло собой линию, отделявшую ОДР от остальной части простран-

ства. В результате была получена замкнутая ОДР в виде многоугольника,

внутри которого затем искалось значение экстремума. Для поиска экстрему-

ма обычно выбирают некоторую величину шага по каждой переменной

x ,

x , …,

x (шаги могут быть одинаковыми или разными) и производят вы-

числения экстремума в различных точках. Суть различных методов оптими-

зации заключается в том, чтобы уменьшить число шагов (итераций) при вы-

числении экстремумов до разумной величины, а по возможности сделать ми-

нимально достаточным.

Можно выделить три основных варианта ОДР в зависимости от типа

ограничений, которые её определяют:

1) ограничения противоречивы, т. е.

x ,

x , …,

x не могут одновремен-

но удовлетворить всем заданным ограничениям, поэтому задача оптимизации

не имеет решения;

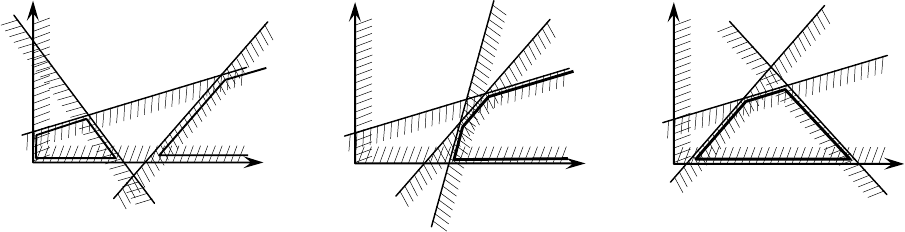
2) ограничения непротиворечивы, но ОДР бесконечна (Рисунок 5.3, б),

поэтому задача оптимизации также не имеет ни постановки, ни решения;

3) ограничения непротиворечивы и ОДР ограничена (Рисунок 5.3, в), по-

этому задача оптимизации имеет решение, именно этот случай рассматрива-

ется далее.

ОДР

а) ОДР не существует б) неограниченная ОДР в) ограниченная ОДР

Рисунок 5.3 — Типы области допустимых решений (ОДР)

На графиках (Рисунок 5.3) штриховкой показана та сторона относитель-

но прямой, в которой располагаются допустимые значения переменных.

На графике (Рисунок 5.3,а) ОДР разорвана и состоит из двух частей: од-

на область ограничена осями координат

x и

x и прямыми

q и

q , вто-

рая — осью координат

x и прямыми

q и

q . Очевидно, что искомая точка

не может быть одновременно в этих двух областях.

На графике (Рисунок 5.3,б) ОДР открыта (показана жирной ломаной) и

устремлена в бесконечность.

На графике (Рисунок 5.3,в) ОДР представляет собой выпуклый много-

угольник.

Линейность целевой функции и ограничений существенно упрощает по-

иск экстремума. Во-первых, ОДР всегда оказывается выпуклой, т. е. такой, в

которой обязательно существует глобальный экстремум. Во-вторых, имеется

возможность использовать матричные методы вычислений, что существенно

облегчает разработку алгоритмов. В-третьих, если решение имеется, оно мо-

жет быть получено как угодно точно за приемлемое количество шагов.

Возникает вопрос: часто ли реальные процессы могут быть представле-

ны как задачи ЛП, т. е. насколько значительна роль ЛП в реальных расчётах?

В реальности большинство процессов, для которых ищутся экстремумы,

описываются нелинейными функциями (целевыми или ограничений), но ча-

сто можно пренебречь некоторыми нелинейными составляющими и тогда

получается линейная задача. В её рамках с помощью методов ЛП можно по-

лучить оптимальную точку, как говорят, в первом приближении, а затем

учесть отброшенные нелинейные члены и перейти к задаче нелинейного про-

граммирования, имея начальное приближение. Кроме этого, многие реальные

задачи по своей природе сами по себе являются линейными. Именно поэтому

линейное программирование играет большую роль в решении задач оптими-

зации и в исследовании операций.

Одним из достоинств линейности задач ЛП является возможность раз-

работки унифицированных алгоритмов. Для этого целесообразно также фор-

мальную постановку задачи ЛП сделать унифицированной. Различают 3

унифицированные формы постановки задачи ЛП:

1) симметрическую первую;

2) симметрическую вторую;

3) каноническую.

В унифицированных формах присутствует только какой-то один тип

ограничений: в симметрической первой — неравенства типа "меньше или

равно"; в симметрической второй — неравенства типа "больше или равно"; в

канонической — только равенства. Все они могут быть получены из общей

формы задачи ЛП путём несложных преобразований, а потому математиче-

ски эквивалентны между собой.

Симметрическая первая форма:

целевая функция:

 

max

2211







iinn

xcxcxcxcxI  ;

ограничения:

 

iiknnkkkk

bxaxaxaxaxq 





,,22,11,

 ,

,...,



;

неотрицательность всех переменных: 0},,,{



xxx



Симметрическая вторая форма:

целевая функция:

 

min

2211







iinn

xcxcxcxcxI  ;

ограничения:

 

iiknnkkkk

bxaxaxaxaxq 





,,22,11,

 ,

,...,



;

неотрицательность всех переменных: 0},,,{



xxx



Каноническая форма:

целевая функция:

 

extr

2211







iinn

xcxcxcxcxI  ;

ограничения:

 

iiknnkkkk

bxaxaxaxaxq 





,,22,11,

 ,

,...,



;

неотрицательность всех переменных: 0},,,{



xxx



Рассмотрим особенности каждой формы.

Видно, что в симметрической первой форме целевая функция максими-

зируется, а ограничения имеют знак "меньше или равно", в симметрической

второй форме — наоборот: целевая функция минимизируется, а ограничения

имеют знак "больше или равно". Т. е. знаки экстремума и ограничений про-

тивоположны. Это — логично. Если функция возрастает, то, возможно, бу-

дут возрастать и переменные, которые должны быть ограничены сверху

("меньше или равно"). Если же, наоборот, функция уменьшается, то, возмож-

но, будут уменьшаться и переменные, которые на этот раз должны ограничи-

ваться снизу ("больше или равно"). На самом деле, обе формы легко преобра-

зуются одна в другую умножением обеих частей целевой функции и ограни-

чений на минус единицу, что приводит к смене знаков.

Характерным является также то, что все переменные принимаются не-

отрицательными. Это позволяет рассматривать их только в первом квадранте

системы координат, что существенно упрощает понимание методов вычис-

лений и построение по ним алгоритмов и программ.

Если использовать неунифицированные формы, то в алгоритмах необ-

ходимо предусмотреть все сочетания всех ограничений и их становится мно-

го. Унификация позволяет исключить необходимость рассмотрения различ-

ных сочетаний.

Сложнее дело обстоит с канонической формой, в которой отсутствуют

неравенства. Если в исходной общей форме неравенства отсутствовали и бы-

ли только равенства, то каноническая форма получается просто. Но если там

были неравенства, то преобразование неравенств в равенства становится от-

дельной задачей, которая решается следующим образом.

Рассмотрим неравенство типа "меньше или равно":

bxaxaxa







2211

Левая часть этого выражения отличается от правой в меньшую сторону,

поэтому для превращения его в равенство необходимо в левую часть доба-

вить некоторую величину — новую переменную

1n

x , которая должна быть

неотрицательной:

bxxaxaxa

nnn





12211



, 0



n

x .

Значение этой новой переменной неизвестно, как и значения других пе-

ременных, поэтому в этом смысле она оказывается с ними в равных услови-

ях. Если имеется несколько ограничений "меньше или равно" (например,

то необходимо в каждое добавить свою дополнительную переменную:





 















;

,22,11,

22,222,211,22

11,122,111,11

mmnnnmmmm

nnn

bxxaxaxaxq



или в краткой форме:

 

kkn

iikk

bxxaxq 





















,...,



Рассмотрим неравенство типа "больше или равно":

bxaxaxa







2211

Левая часть этого выражения отличается от правой в большую сторону,

поэтому для превращения его в равенство необходимо из левой части вы-

честь некоторую величину — новую переменную

1n

x , которая должна быть

неотрицательной:

bxxaxaxa

nnn







12211



, 0



n

x .

Значение этой новой переменной неизвестно, как и значения других пе-

ременных, поэтому в этом смысле она оказывается с ними в равных услови-

ях. Если имеется несколько ограничений "больше или равно" (например,

то необходимо в каждое добавить свою дополнительную переменную:





 















;

,22,11,

22,222,211,22

11,122,111,11

mmnnnmmmm

nnn

bxxaxaxaxq



или в краткой форме:

 

kkn

iikk

bxxaxq 





















,...,



Целевая функция в любом случае остаётся той же, что и в исходной об-

щей форме:





extr

2211







xcxcxcxI



, т. е. может как максимизиро-

ваться, так и минимизироваться. Во всех случаях все переменные должны

быть неотрицательными: 0



x ,

)

(







Все переменные должны присутствовать в целевой функции, поэтому

переменные, дополнительно введённые в ограничения, формально записы-

ваются в целевой функции с коэффициентами 0:





















 mnnnnn

xxxxcxcxcxI 000

212211



extr0











xxc .

Переменные

x ,

x , … ,

x — основные, переменные

1n

x ,

2n

x ,…,



— дополнительные или вспомогательные.

На дополнительные переменные всегда накладываются ограничения не-

отрицательности, так как это следует из их физической сути, а их реальный

знак вводится в соответствующих выражениях.

На некоторые из основных переменных по условиям задачи может быть

не наложено ограничений неотрицательности. Тогда для перехода к канони-

ческой форме используют следующий приём: каждую такую переменную за-

меняют разностью двух вспомогательных неотрицательных переменных:

.0,0,















kkkkk

xxxxx

Таким образом добиваются того, что все переменные — основные и

вспомогательные — имеют ограничения неотрицательности. Это делается

для того, чтобы упростить построение алгоритмов.

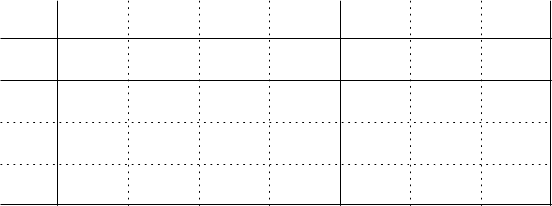
Поскольку каноническая форма содержит теперь только однородные

ограничения типа равенств, все их можно записать в матричной форме.

Например, при четырёх исходных переменных и трёх ограничениях матрица

будет иметь вид:

100

010

001

000

4,33,32,31,33

4,23,22,21,22

4,13,12,11,11

4321

7654321

aaaaq

ccccI

xxxxxxx

где в строке

записаны коэффициенты

c для первых



переменных

(

x …

x ) и нули для дополнительных



переменных (

x …

x ); в строках

q ,

q записаны коэффициенты из ограничений, причём в левом нижнем

прямоугольнике — коэффициенты при основных переменных, а в правом

нижнем прямоугольнике — коэффициенты при дополнительных переменных

(в данном случае предполагается, что исходные неравенства были типа

"больше или равно", в случае неравенств типа "меньше или равно" стояли бы

значения –1). Матрица с коэффициентами при дополнительных переменных

всегда квадратная, диагональная и единичная. Матрица коэффициентов при

основных переменных в общем случае не квадратная.

Целевая функция для рассматриваемого случая:





76544332211

000 xxxxcxcxcxcxI















Ограничения в случае исходных неравенств типа "больше или равно":





 













344,333,322,311,33

244,233,222,211,22

144,133,122,111,11

;

bxaxaxaxaXq

bxaxaxaxaxq

они приводятся к канонической форме:





 













;

3744,333,322,311,33

2644,233,222,211,22

1544,133,122,111,11

bxxaxaxaxaxq

т. е. новые переменные попадают в равенства канонической формы со знаком

"минус".

В случае исходных неравенств типа "меньше или равно":





 













344,333,322,311,33

244,233,222,211,22

144,133,122,111,11

;

bxaxaxaxaxq

они приводятся к канонической форме:





 













;

3744,333,322,311,33

2644,233,222,211,22

1544,133,122,111,11

bxxaxaxaxaxq

т. е. новые переменные попадают в равенства канонической формы со знаком

"плюс".

Переменные

x ,

x — основные, переменные

x ,

x — дополни-

тельные или вспомогательные.

Пример 5.2. Следующую задачу ЛП привести к каноническому виду:

extr;23)(

321







xxxxI

















;23

;53

;32

321

xxx

.0,0



Таким образом, имеется целевая функция (в ней пока не задан тип экс-

тремума), имеются три ограничения: типа равенства, типа неравенства

"меньше или равно" и типа неравенства "больше или равно". Имеются также

ограничения на неотрицательность двух из трёх переменных (

x и

x ). Тре-

тья переменная (

x ) может быть любой.

Решение. Первое ограничение имеет вид равенства, поэтому оно остаёт-

ся без изменений:





xx .

Второе ограничение — неравенство типа "меньше или равно". Оно при-

водится к равенству введением дополнительной переменной

x со знаком

"плюс":











;53

4321

xxxx

Третье ограничение — неравенство типа "больше или равно". Оно при-

водится к равенству введением дополнительной переменной

x со знаком

"минус":











;23

531

xxx

В обоих последних случаях вводятся дополнительные ограничения не-

отрицательности для введённых дополнительных переменных:

x ,

x .

На основную переменную

x не было по условиям задачи наложено

ограничение неотрицательности. Чтобы разрешить эту проблему, вводятся

ещё дополнительные переменные:

0,0,

22222















xxxxx .

Итого задача содержит шесть переменных. В целевой функции пред-

ставлены 3 из них, поэтому формально в целевую функцию необходимо вве-

сти дополнительные переменные. Дополнительные переменные



встают на место переменной

x и имеют соответствующий коэффициент.

Дополнительные переменные

x и

x вводятся в целевую функцию с коэф-

фициентами 0. Каноническая форма задачи окончательно имеет следующий

вид:

100





































.0,,,,,

;23

;5223

extr;00223)(

543221

531

43221

543221

xxxxxx

xxx

xxxxx

xxxxxxxI

Каноническая форма позволяет использовать матричные методы.

5.3 Симплекс-метод решения задачи линейного программи-

рования

Слово симплекс происходит от латинского simplex, означающее "про-

стой". В данном случае оно означает "простой выпуклый многогранник" с

числом граней, равным числу измерений. В нульмерном случае таковым объ-

ектом является точка, в одномерном — отрезок прямой, в двумерном — тре-

угольник, в трёхмерном — тетраэдр и т. д. Смысл термина симплекс приме-

нительно к задаче линейного программирования в том, что искомая точка оп-

тимального решения всегда находится в вершине выпуклого многогранника,

образованного пересечением линий (плоскостей) ограничений. Поиск опти-

мальной точки осуществляется определением координат всех вершин много-

гранника и нахождением в каждой из них значения целевой функции. Затем

значения целевой функции сравниваются между собой и ищется наибольшее

(если решается задача максимизации) или наименьшее (если решается задача

минимизации). Соответствующая точка (со своими координатами, которые

известны) и будет оптимальным в данном смысле решением задачи линейно-

го программирования.

В наиболее простом случае возможен простой перебор точек и решение

всегда будет найдено. Проблема возникает, если задача имеет большое число

ограничений, что часто бывает на практике. Например, при числе основных

переменных



и числе ограничений



имеется 6 угловых точек и их

простой перебор не представляет сложности. Но при числе основных пере-

менных



и числе ограничений



необходимо решить

184756

 CC

систем уравнений размерности 10×10. Такая задача уже

представляет проблему для ЭВМ среднего класса. Тогда возникает научная

задача упорядочения перебора, чтобы избежать расчётов явно худших вари-

антов. Одна из идей заключается в том, чтобы выбрать начальную точку слу-

чайным образом, а последующие выбирать так, чтобы решение каждый раз

было лучше предыдущего: при максимизации значение целевой функции

должно каждый раз возрастать, а при минимизации — уменьшаться. При