Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.

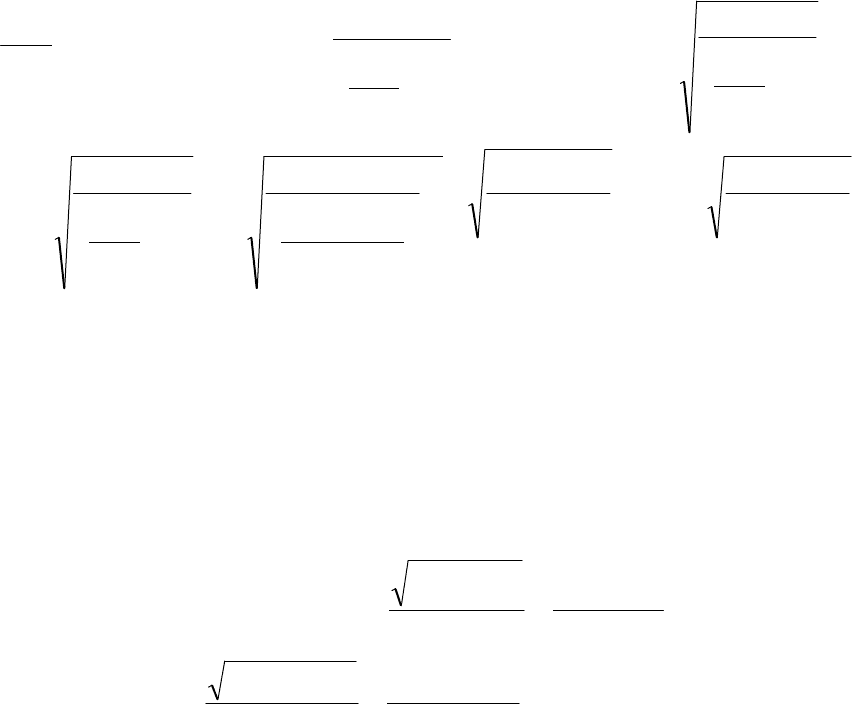
11
2
2
2
2
1 H
v
v
x
вод
суш
,
1
2
2
2
2
вод
суш
v
v
H
x ,
1
1
2
2
вод
суш
v
v
Hx ;
2222
2
2
22
2
2
11
1
1
водсуш
вод
водсуш
вод
вод
водсуш
вод
суш
opt
vv
Hv
vv
v
H
v
vv
H
v
v
Hx
,
где из двух возможных корней выбран положительный, так как отрицатель-
ный корень означает, что точка причаливания должна располагаться левее
начала координат, что удлиняет путь как по морю, так и по суше, а потому
явно не может считаться наилучшим решением.
Для указанных выше параметров расстояние до точки причаливания
opt
x =8,041 км, а наименьшее время в пути, час:
суш
opt
вод
opt
opt
v
xL
v
xH
TxT
)(
)041,8()(
22
.177,4
6
)041,815(
4
041,89
22
час
Найденное значение расположения точки
opt
x называется оптимальным,
а зама задача — задачей оптимизации или задачей оптимального выбора. В
данном случае — это оптимальный выбор точки причаливания.
При решении таких задач характерным является следующее:
имеется критерий оптимальности для сравнения различных вариантов
(в данном случае — минимум времени движения);
в задаче содержится противоречие — если точка причаливания левее
наилучшей точки, то удлиняется путь по берегу, а если точка причаливания
правее наилучшей — то замедляется движение (в этом случае бóльшую часть
пути приходится плыть), и в обоих случаях увеличивается время движения
по сравнению с наилучшим вариантом;
составляется математическая модель движения в виде некоторой функ-
ции, которая называется целевой функцией, связывающей время движения
(критерий) с искомой координатой
x
точки причаливания;
целевая функция имеет экстремум, в данном случае — минимум;
этот минимум один;
12
используется аппарат математического анализа — дифференцирование
целевой функции, приравнивание полученного выражения нулю и решение
полученного уравнения с определением его корня;
имеется ограничение — координата искомой точки
x
не может быть от-
рицательной (так как отрицательная координата явно увеличит время движе-
ния).
В целом можно выделить следующие три основные составляющие, де-
лающие задачу оптимизационной: 1) наличие критерия; 2) наличие противо-
речия; 3) наличие целевой функции в сочетании с ограничениями.
С математической точки зрения после формулирования оптимизацион-
ной задачи её решение сводится к поиску экстремума целевой функции.
С точки зрения характера поведения, функции классифицируют, как
обычные функции в математическом анализе:
функции одной переменной и нескольких переменных;
функции гладкие и негладкие (у гладких функций существует, по
крайней мере, первая производная);
функции с одним экстремумом или с несколькими экстремумами од-
ного типа (минимумами или максимумами).
Пример функции одной переменной:
2
35)( xxI .
Пример функции двух переменных:
2121
35),( xxxxI
Если
1
n
и вектор имеет лишь одну переменную, то все построения
легко делать графически, изображая
)
(
x
I
в зависимости от
x
. Если
2
n
и
имеются две переменные
1
x и
2
x , то можно изобразить поверхность, отра-
жающую значения ),(
21
xxI в зависимости от изменения
1
x и
2
x . Если
3
n
,
т. е. переменных три и более, то графически изобразить целевую функцию
оказывается невозможно.
1.2 Формальная постановка задачи оптимизации, базовые
понятия и определения
С математической точки зрения, процесс оптимизации представляет со-
бой поиск экстремума (максимума или минимума) целевой функции
)
(
x
I
,
которая отражает зависимость некоторой величины, которую нужно миними-
зировать или максимизировать (время, стоимость, расстояние, прибыль и
др.), от влияющих на это факторов
x
. При этом ищется в первую очередь
точка экстремума
x
(значения факторов, при которых достигается экстре-
мум), а затем само значение целевой функции в этой точке )(
xI .

13
Это может быть представлено в следующем виде: задана целевая функ-
ция
)
(
x
I
, где
x
— вектор в
n
R
на множестве допустимых решений
X
(
X
x
,
n
RX ); необходимо найти вектор
x
, являющийся точкой экстре-
мума (минимума или максимума) целевой функции: )(extr)( xIxI
Xx
: при
минимизации: )(min)( xIxI
Xx
; при максимизации: )(max)( xIxI
Xx
.
Пояснения.
1. Запись
n
R
означает
n
-мерное евклидово пространство, т. е. простран-
ство всех обычных действительных (реальных — отсюда и обозначение
R
)
чисел, имеющее
n
переменных. При
1
n
получается обычная функция с од-
ной переменной, при
2
n
получается плоскость двух переменных, при
3
n
— пространство трёх переменных и т. д. Фактически, указание на
R
не
имеет в данном случае значения, так как решение обычно ищется именно
среди действительных чисел, важно лишь указать величину
n
, так как от это-
го иногда зависят конкретные формулы для поиска решений. Но с формаль-
ной точки зрения в математике существуют также множества других чисел:
комплексных, целых, строго положительных, строго отрицательных, в каком-
то диапазоне и др. Каждое множество имеет своё обозначение.
2. Вектор
T
n
n
xxx
x
x
x
x ),,,(
21
2
1
. Знак
T
означает операцию транспо-
нирования, чтобы изображать вектор в развёрнутой форме не в виде столбца,
а в виде строки — так удобнее записывать его в тексте.
3. Вектор, который соответствует точке экстремума, обозначается звёз-
дочкой:
T
n
xxxx ),,,(
21
. Соответствующая функция в этой точке: )(
xI .
4. Выражение
X
x
означает, что вектор
x
принадлежит множеству
допустимых решений
X
. Выражение
n
RX означает, что поиск конкрет-
ных значений
x
должен производиться только в некотором множестве до-
пустимых решений
X
, которое содержится в
n
R
. Выражение
n
RX распа-
дается на два подвыражения:
n
R
X
, т. е. когда
X
полностью покрывает
n
R
, и
n
R
X
, когда множество
X
покрывает только часть всего множества
действительных чисел
n
R
. В случае
n
R
X
на искомый вектор
x
не накла-
дывается ограничений (любая точка множества
n
R
может оказаться иско-

14
мой), а в случае
n
R
X
имеются ограничения (не всякая точка множества
n
R
может оказаться искомой). Условие
n
RX является общим для поста-
новки задачи оптимизации, которая с методологической точки зрения разде-
ляется на два варианта: решение задачи на безусловный экстремум с
n
R
X
и решение задачи на условный экстремум
n
R
X
. Эти задачи имеют раз-
личные подходы к решению.
5. В результате решения оптимизационной задачи можно получить раз-
личные результаты:
единственную точку экстремума, если функция имеет одну выпук-
лость, например, парабола
2
)( xxI ;
множество точек экстремума, если функция имеет несколько выпукло-
стей, например, синусоида
)
sin(
)
(
x
x
I
;
ни одной точки экстремума, если функция монотонно возрастает или
убывает, например, линейная функция
x
x
I
2
)
(
.
При этом возможны также варианты. Например, при наличии несколь-
ких экстремумов все они могут иметь одну и ту же величину [синусоида
)
sin(
)
(
x
x
I
] или разную величину [затухающая синусоида )sin()( xexI
x
].
При отсутствии экстремумов функция может изменяться [
x
x
I
)
(
] или оста-
ваться постоянной [
5
)
(
x
I
].
При наличии нескольких экстремумов один из них может быть больше
(меньше) других и тогда это — глобальный экстремум, остальные экстрему-
мы — локальные экстремумы. Формальное определение глобального и ло-
кального экстремумов следующее:
точка
X
x
называется точкой глобального (абсолютного) миниму-
ма функции
)
(
x
I
на множестве
X
, если функция достигает в этой точке сво-
его наименьшего значения: )()( xIxI
,
X
x
;
точка
X
x
называется точкой глобального (абсолютного) макси-
мума функции
)
(
x
I
на множестве
X
, если функция достигает в этой точке
своего наибольшего значения: )()( xIxI
,
X
x
.
Запись
X
x
читается: "для всех векторов
x
, принадлежащих множе-
ству
X
". Характерно, что здесь используется знак нестрогого неравенства
(больше или равно, меньше или равно). Это означает, что, например, синусо-
ида имеет много абсолютных максимумов (и абсолютных минимумов), кото-
рые равны между собой.
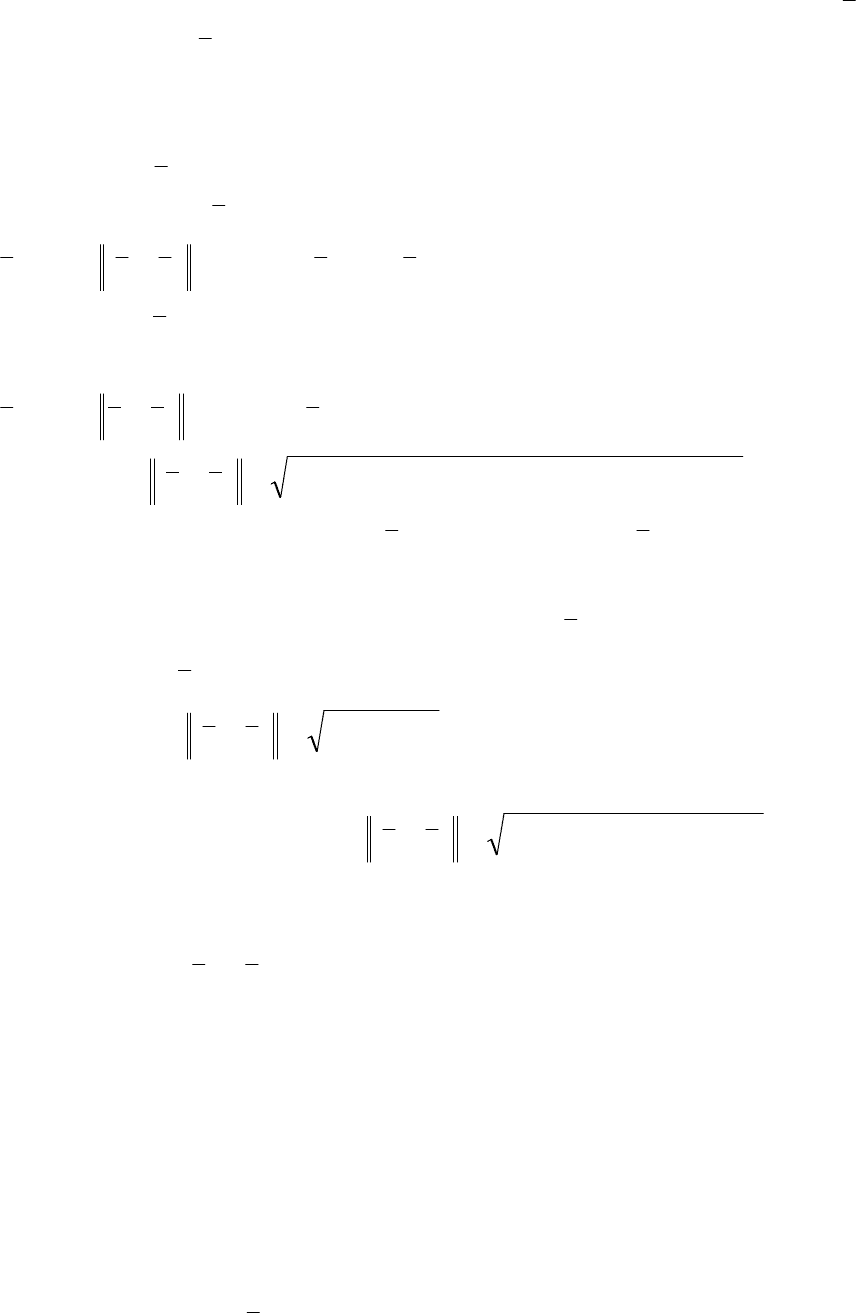
15
Более сложным является определение локального экстремума. Локаль-
ным считается экстремум на ограниченном интервале изменения
x
. При
этом функция
)
(
x
I
должна быть больше (если ищется минимум) или меньше
(если ищется максимум) своих значений в соседних точках в пределах этого
интервала:
точка
X
x
называется точкой локального (относительного) мини-
мума функции
)
(
x
I
на множестве
X
, если существует
0
е
, такое, что если
X
x
и
xx , то )()( xIxI
;
точка
X
x
называется точкой локального (относительного) макси-
мума функции
)
(
x
I
на множестве
X
, если существует
0
е
, такое, что если
X
x
и
xx , то )()( xIxI
.
Здесь
22
22
2
11
)()()(
nn
xxxxxxxx — евклидова
норма вектора разности между
T
n
xxxx ),,,(
21
и
T
n
xxxx ),,,(
21
, т. е.
расстояние между двумя точками в пространстве, определяемыми этими век-
торами. Первая точка задаётся координатами
T
n
xxxx ),,,(
21
, а вторая —
координатами
T
n
xxxx ),,,(
21
. Если
1
n
, т. е. вектор имеет только одну
координату, то ||)(
11
2
11
xxxxxx — просто длина (модуль дли-
ны, так как извлекается квадратный корень из квадрата). Если
2
n
, т. е. век-
тор имеет две координаты, то
2
22
2
11
)()(
xxxxxx — гипотену-
за прямоугольного треугольника. При бóльших значениях
n
смысл получен-
ного выражения менее нагляден, но всё равно соответствует расстоянию
между точками
x
и
x
. Это расстояние должно быть внутри некоторого кру-
га, очерченного с радиусом
(поскольку это радиус круга, то
принимается
положительной и не равной нулю величиной). Несмотря на то, что перемен-
ных может быть много, всё равно получается круг (а не шар и т. д.), так как
норма вектора есть число.
Глобальный экстремум всегда является одновременным локальным, а
локальный — не всегда является глобальным.
При анализе целевой функции на экстремум оказывается полезным по-
нятие линии или поверхности одного уровня, т. е. совокупности точек, при
которых функция
)
(
x
I
имеет одно и то же значение. Формально ищутся ре-
16
шения уравнений
const
)
(
x
I
, где вместо постоянной величины
const
по-
следовательно подставляется то или иное значение.
Общая методика поиска экстремума заключается в том, чтобы найти
производную целевой функции, приравнять нулю и найти решение. Если це-
левая функция зависит только от одной переменной, то всё сравнительно
просто. А если имеется много переменных, то необходимо вместо производ-
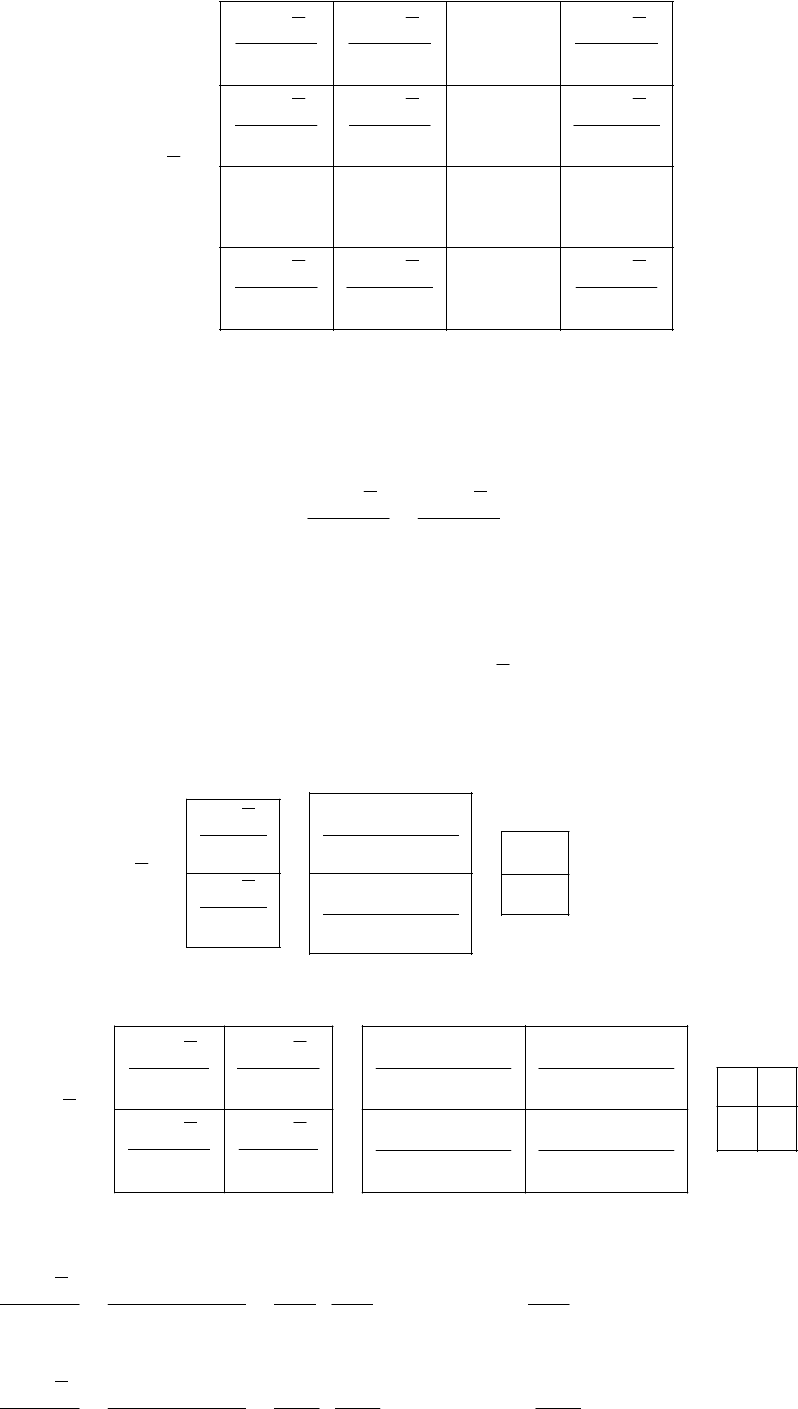
ной находить градиент функции:
T
n
n
x
xI
x
xI
x
xI
x
xI
x
xI
x
xI
xI
)(
,,
)(
,
)(
)(
)(
)(
)(
21
2
1
,
где значок
называется набла
1
(перевёрнутая дельта).
Фактически, это — производная функции по всем переменных. Очевид-
но, что для использования градиента необходимо, чтобы целевая функция
была хотя бы однократно дифференцируема по каждой переменной.
Если затем такую функцию (а она представляет собой уже вектор) при-
равнять нулю (
0
)
(
x
I
), то её решение даст точку
T
n
xxxx ),,,(
21
в
пространстве, в которой функция
)
(
x
I
имеет экстремум. Но является ли он
максимумом или минимумом, не ясно. Чтобы уточнить это, берут вторую
производную и определяют её знак в найденной точке
x
. Если вторая про-
изводная больше нуля, это означает, что первая производная увеличивается
справа от точки экстремума
x
, т. е. имеет место минимум. Если вторая про-
изводная меньше нуля, это означает, что первая производная уменьшается
справа от экстремума
x
, т. е. имеет место максимум. Это сравнительно про-
сто для целевой функции, зависящей от одной переменной. Если имеется не-
сколько переменных, то вторую производную брать более сложно и тогда
вводится понятие матрицы Гессе:
1
По-гречески νάβλα, что в переводе означает "арфа", форму которой напоминает (с точки зрения греков)
значок
17
2
2
2
2
1
2
2
2
2
2
2
12
2
1
2
21
2
2
1
2
)()()(
)()()(
)()()(
)(
n
nn
n
n
x
xI
xx
xI
xx
xI
xx
xI
x
xI
xx
xI
xx
xI
xx
xI
x
xI
x
H
.
Матрица Гессе формируется из двукратно продифференцированных вы-
ражений целевой функции. Матрица всегда квадратная и симметричная, так
как в соответствии с правилами дифференцирования выполняется:
ikki
xx
xI
xx
xI
)()(
22
.
Матрица Гессе используется для определения типа экстремума при ана-
лизе целевых функций, зависящих от нескольких переменных.
Пример 1.2. Дана целевая функция
2
2
2
1
3)( xxxI . Требуется найти
градиент и матрицу Гессе.
Градиент:
T
xx
x
x
x
xx
x
xx
x
xI
x
xI
xI
21
2
1
2
2
2
2
1
1
2
2
2
1
2
1
6,2
6
2
)3(
)3(
)(
)(
)(
.
Матрица Гессе:
60
02
)3()3(
)3()3(
)()(
)()(
)(
2
2
2
2
2
1
12
2
2
2
1
21
2
2
2
1
2
1
2
2
2
1
2
2
2
12
2
21
2
2
1
2
x
xx
xx
xx
xx
xx
x
xx
x
xI
xx
xI
xx
xI
x
xI
xH ,
где значения производных находятся следующим образом:
223
)3(
)(
1
1
2
2
2
1
11
2
1
2
2
2
1
2
1
2
x
x
xx
xx
x
xx
x
xI
;
663
)3(
)(
2
2
2
2
2
1
22
2
2
2
2
2
1
2
2
2
x
x
xx
xx
x
xx
x
xI
;
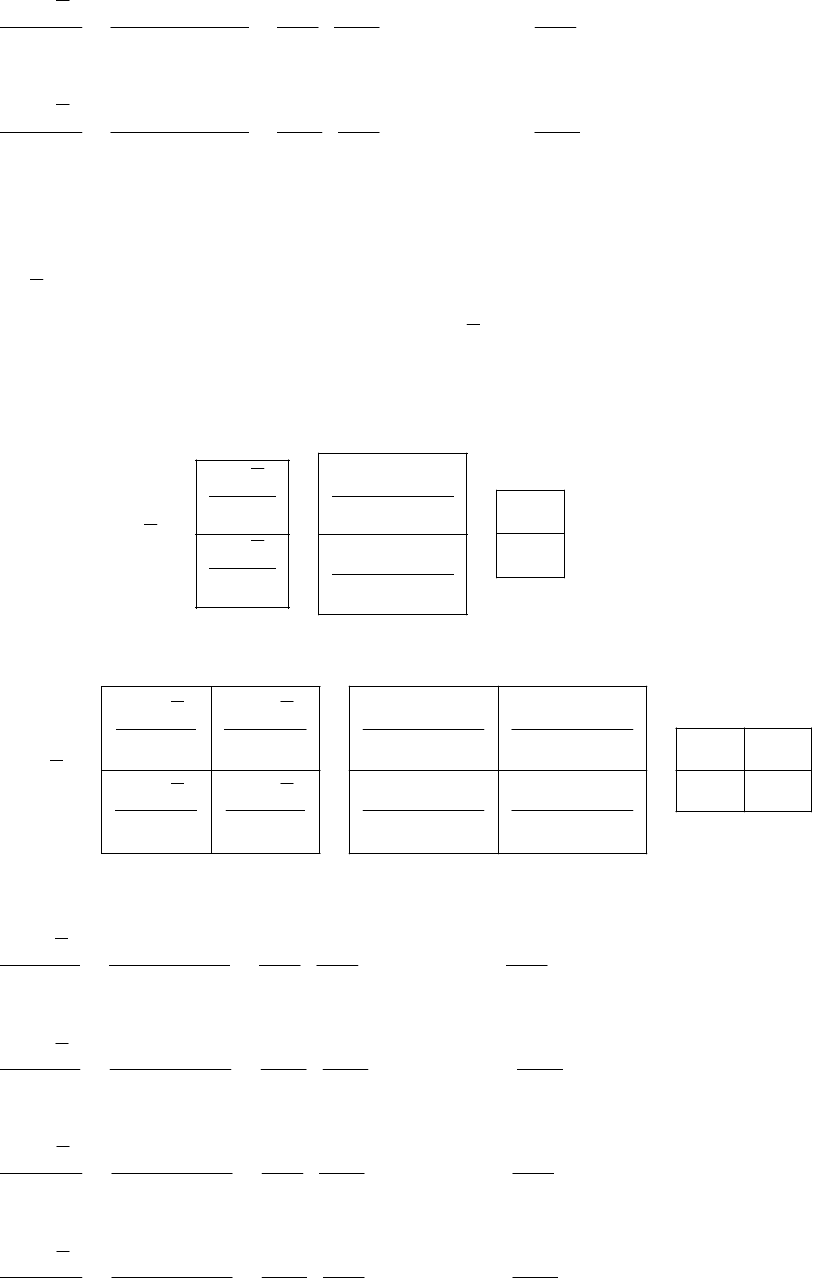
18
063
)3(
)(
2
1
2
2
2
1
2121
2
2
2
1
21
2
x
x
xx
xxxx
xx
xx
xI
;
023
)3(
)(
1
2
2
2
2
1
1212
2
2
2
1
12
2
x
x
xx
xxxx
xx
xx
xI
,
В данном случае вид целевой функции таков, что после двукратного
дифференцирования получаются числа, но, вообще говоря, могут быть функ-
ции от
x
.
Пример 1.3. Дана целевая функция
3
2
2
1
)( xxxI . Требуется найти гра-
диент и матрицу Гессе.
Градиент:
T
xx
x
x
x
xx
x
xx
x
xI
x
xI
xI
2
21
2
2
1
2
3
2
2
1
1
3
2
2
1
2
1
3,2
3
2
)(
)(
)(
)(
)(
.
Матрица Гессе:
2
2
2
3
2
2
1
12
3
2
2
1
21
3
2
2
1
2
1
3
2
2
1
2
2
2
12
2
21
2
2
1
2
60
02
)()(
)()(
)()(
)()(
)(
x
x
xx
xx
xx
xx
xx
x
xx
x
xI
xx
xI
xx
xI
x
xI
x
H ,
где значения производных находятся следующим образом:
2]2[)(
)()(
1
1
3
2
2
1
11
2
1
3
2
2
1
2
1
2
x
x
xx
xx
x
xx
x
xI
;
2
2
2
2
3
2
2
1
22
2
2
3
2
2
1
2
2
2
6]3[)(
)(
)(
xx
x
xx
xx
x
xx
x
xI
;
0]3[)(
)()(
2
2
1
3
2
2
1
2121
3
2
2
1
21
2
x
x
xx
xxxx
xx
xx
xI
;
0]2[)(
)()(
1
2
3
2
2
1
1212
3
2
2
1
12
2
x
x
xx
xxxx
xx
xx
xI
,
В данном случае вид целевой функции таков, что после двукратного
дифференцирования в матрице Гессе получаются как числа, так и функции.

19
При исследовании целевой функции иногда оказывается необходимо
разложить её в ряд Тейлора в окрестности
x
Д
вокруг некоторой точки
0
x
.
Если целевая функция зависит только от одного аргумента, то ряд Тейлора
выглядит следующим образом:
)Δ()()Δ()(
00
xfxfxxfxf
k
k
k
x
dx
xfd
k
x
dx
xfd
x
dx
xdf
xf )Δ(
)(
!
1
)Δ(
)(
!2
1
)Δ(
)(
!1
1
)(
0
2
2
020
0
k
k
xaxaxaa )Δ()Δ()Δ(
2
210
,
где
k
a — постоянные коэффициенты; первые три составляющие — нулевая,
линейная и квадратичная относительно приращения
x
Δ
; при разложении в
ряд Тейлора необходимо вычислить коэффициенты
k
a перед этими прира-
щениями, для чего берутся соответствующие производные функции и в них
подставляется значение
0
x
x
, поэтому ряд Тейлора представляет собой
сумму приращений различной степени (от нулевой до бесконечной).
В математическом анализе реально используют несколько первых чле-
нов ряда — обычно только первый, только первые два или только первые
три. Если используется только первый член ряда, то получают не функцию (в
полученном выражении нет переменных), а число, равное значению функции
в точке разложения в ряд. Если используют первые два слагаемых, то полу-
чают линейную функцию относительно приращения, а если используют пер-
вые три слагаемых ряда, то — квадратичную функцию. Таким образом, лю-
бую сколь угодно сложную функцию можно представить постоянным чис-
лом (в конкретной точке), линейной функцией или квадратичной функцией
вблизи конкретной точки. Разумеется, это справедливо только в некоторой
малой области слева и справа от точки разложения. Но саму эту точку можно
перемещать и пересчитывать коэффициенты, тогда можно пользоваться раз-
ложением Тейлора во всей области допустимых решений.
Если целевая функция зависит от нескольких переменных, то ряд Тей-
лора выглядит следующим образом:
)Δ()()Δ()(
00
xIxIxxIxI
xxxxxIxI
xx
T
xx
T
Δ)(Δ
!2
1
Δ)(
!1
1
)(
0
0
0
H
xxxxxIxI
TT
Δ)(Δ
!
2
1
Δ)(
!
1
1
)(
000
H ,
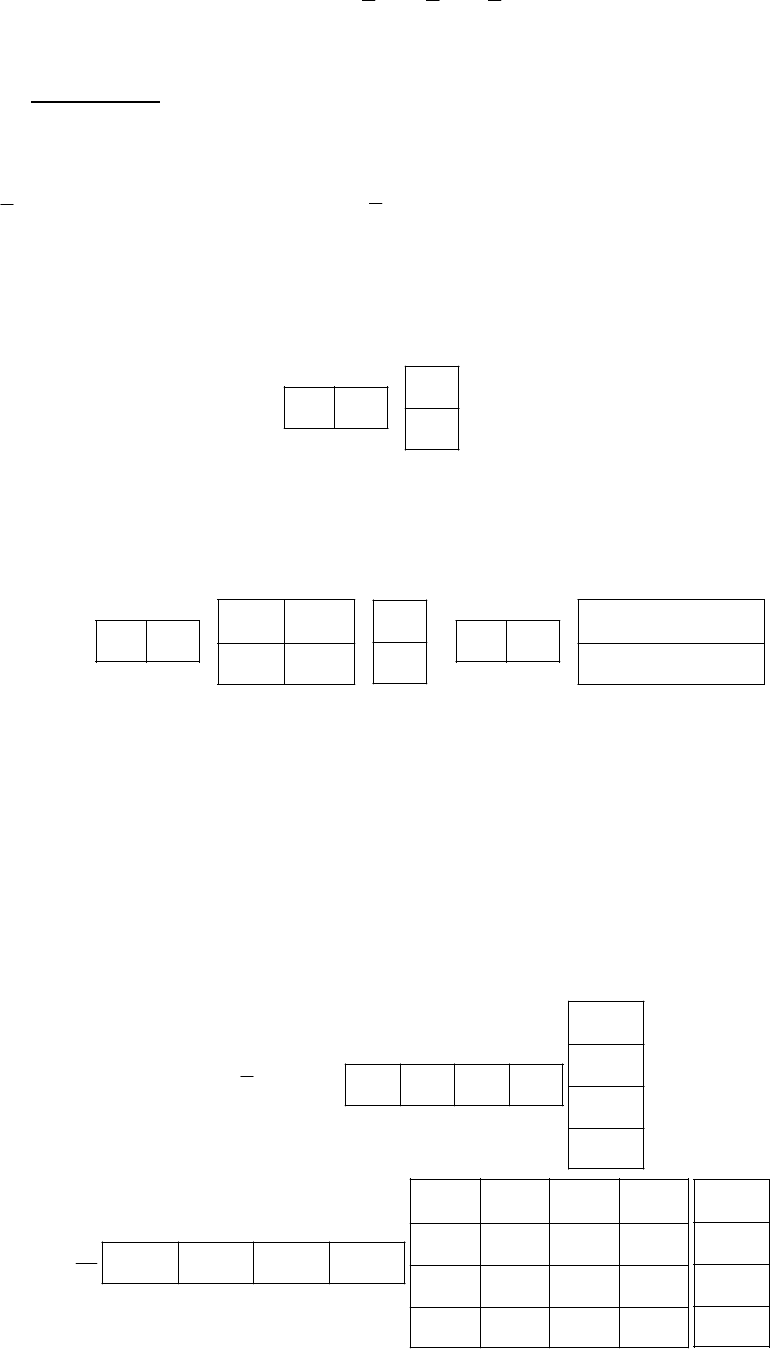
20
где вместо первой производной используется градиент, а вместо второй про-
изводной — матрица Гессе; xxx
T
Δ)(Δ
0
H называется квадратичной фор-
мой.
Пояснения. Квадратичная форма в матричном исчислении является ана-
логией квадрата в обычном математическом анализе. Название "квадратич-
ная форма" связано с тем, что произведение двух векторов (вектора-строки
T
x
Д
слева и вектора-столбца
x
Д
справа), содержащих одни и те же состав-
ляющие (поскольку это — один и тот же вектор, но слева он транспониро-
ван), дадут при перемножении квадраты этих составляющих. Например, при
наличии у вектора двух составляющих:
)(
2
2
2
1
2
1
21
xx
x
x
xx ,
т. е. в результате получаются только квадраты составляющих векторов.
Если между этими векторами стоит матрица, то результат перемножения
будет, например, таким:
22,211,2
22,111,1
21
2
1
2,21,2
2,11,1
21
xaxa
xaxa
xx
x
x
aa
aa
xx
)()(
22,211,2222,111,11
xaxaxxaxax
2
22,2211,22,1
2
11,1
2
22,2211,2212,1
2
11,1
)( xaxxaaxaxaxxaxxaxa ,
т. е. в результате получаются квадраты составляющих вектора и их произве-
дения.
При большем количестве составляющих (трёх, четырёх и т. д.) появятся
все возможные комбинации их парных произведений, включая квадраты.
В развёрнутом виде:
n
n
x
x
x
aaaIxI
Δ
Δ
Δ
)(
2
1
210
n
nnnn
n
n
n
x
x
x
hhh
hhh
hhh
xxx
Δ
Δ
Δ
ΔΔΔ
!2
1
2
1
,2,1,
,22,21,2
,12,11,1
21
,
