Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.

31
0)(
xI .
Если матрица Гессе функции
)
(
x
I
является положительно определён-
ной, т. е.
0)(
xH ,
то точка
x
есть точка локального минимума, а если матрица Гессе функции
)
(
x
I
является отрицательно определённой, т. е.
0)(
xH ,
то точка
x
есть точка локального максимума.
Что означает положительная (неотрицательная) или отрицательная (не-
положительная) определённость матрицы Гессе? Эти понятия не следует пу-
тать с положительными (или отрицательными) матрицами, у которых все
элементы положительны (или отрицательны). Это — разные понятия и тер-
мины: при положительных элементах матрицы она называется положитель-
ной, а в рассматриваемом случае речь идёт о положительно определённой
матрице.
Имеются специальные алгоритмы выявления знака определённости мат-
рицы, при этом рассматривают определитель матрицы Гессе:
nnnn
n
n
hhh
hhh
hhh
x
,2,1,
,22,21,2
,12,11,1
)(det
H
Но рассматривают не только определитель всей матрицы, а также его уг-
ловые миноры (частные определители):
1,11
Δ
h
,
2,21,2
2,11,1
2
Δ
hh
hh
,
3,32,31,3
3,22,21,2
3,12,11,1
3
Δ
hhh
hhh
hhh
,
nnnn
n
n
n
hhh
hhh
hhh
,2,1,
,22,21,2
,12,11,1
Δ
,
которые получаются из исходной матрицы постепенным увеличением числа
выбираемых элементов от левого верхнего угла до охвата всей матрицы:

32
h
1,1
h
1,2
h
1,3
h
1,4
h
1,5
h
2,1
h
2,2
h
2,3
h
2,4
h
2,5
Δ
k
=
h
3,1
h
3,2
h
3,3
h
3,4
h
3,5
h
4,1
h
4,2
h
4,3
h
4,4
h
4,5
h
5,1
h
5,2
h
5,3
h
5,4
h
5,5
Рассматривают также главные миноры, которые получают из определи-
теля матрицы произвольным вычёркиванием любого одинакового числа
строк и столбцов с одинаковыми номерами:
h
1,1
h
1,2
h
1,3
h
1,4
h
1,5
h
2,1
h
2,2
h
2,3
h
2,4
h
2,5
Δ
k
=
h
3,1
h
3,2
h
3,3
h
3,4
h
3,5
h
4,1
h
4,2
h
4,3
h
4,4
h
4,5
h
5,1
h
5,2
h
5,3
h
5,4
h
5,5
или:
h
1,1
h
1,2
h
1,3
h
1,4
h
1,5
h
2,1
h
2,2
h
2,3
h
2,4
h
2,5
Δ
k
=
h
3,1
h
3,2
h
3,3
h
3,4
h
3,5
h
4,1
h
4,2
h
4,3
h
4,4
h
4,5
h
5,1
h
5,2
h
5,3
h
5,4
h
5,5
или:
h
1,1
h
1,2
h
1,3
h
1,4
h
1,5
h
2,1
h
2,2
h
2,3
h
2,4
h
2,5
Δ
k
=
h
3,1
h
3,2
h
3,3
h
3,4
h
3,5
h
4,1
h
4,2
h
4,3
h
4,4
h
4,5
h
5,1
h
5,2
h
5,3
h
5,4
h
5,5
и т. п.
Здесь затенены вычёркиваемые столбцы и строки матрицы.
Величина вычисляемых при этом определителей (угловых и главных
миноров) не имеет значение, важен их знак.
Критерий проверки достаточных условий экстремума (критерий
Сильвестра):
1. Для того, чтобы матрица Гессе была положительно определённой, т. е.
0)(
xH , и точка
x
являлась точкой локального минимума, необходимо и
достаточно, чтобы знаки угловых миноров были положительны:
0
Δ
1
, 0
Δ
2
, … 0
Δ
n
.

33
Пояснения. "Положительно определённая" означает, что используется
знак строго равенства "больше".
2. Для того, чтобы матрица Гессе была отрицательно определённой, т. е.
0)(
xH , и точка
x
являлась точкой локального максимума, необходимо и
достаточно, чтобы знаки угловых миноров чередовались, начиная с отрица-
тельного:
0
Δ
1
, 0
Δ
2
, 0
Δ
3
, … 0Δ)1(
n
n
,
где выражение 0Δ)1(
n
n
даёт в результате минус, если это нечётный ми-
нор, и плюс, если чётный (если слева будет знак минус, то можно домножить
обе части неравенства на –1 и записанный знак ">" больше заменится на знак
"<" меньше.
Пояснения. "Отрицательно определённая" означает, что используется
знак строго равенства "меньше".
Критерий проверки необходимых условий экстремума второго по-
рядка:
1. Для того, чтобы матрица Гессе была положительно полуопределён-
ной, т. е. 0)(
xH , и точка
x
, возможно, являлась точкой локального ми-
нимума, необходимо и достаточно, чтобы все главные миноры определителя
матрицы Гессе были неотрицательны.
Пояснения. "Положительно полуопределённая" означает, что использу-
ется знак нестрогого неравенства "больше или равно".
2. Для того, чтобы матрица Гессе была отрицательно полуопределённой,
т. е. 0)(
xH , и точка
x
, возможно, являлась точкой локального максиму-
ма, необходимо и достаточно, чтобы все главные миноры определителя мат-
рицы Гессе чётного порядка были неотрицательны, а нечётного порядка —
неположительны.
Пояснения. "Отрицательно полуопределённая" означает, что использу-
ется знак нестрогого неравенства "меньше или равно".
Все рассмотренные условия наличия экстремума используются не толь-
ко при аналитических исследованиях целевой функции, но также при постро-
ении численных методов, где они являются как теоретической базой, так и
частью соответствующих алгоритмов.
34
2.3 Необходимые и достаточные условия условной опти-
мизации
2.3.1 Постановка задачи и основные понятия условной оптимизации
Условная оптимизация отличается от безусловной тем, что дополни-
тельно к целевой функции записываются функции ограничений, т. е. ищется
не просто точка экстремума, а точка экстремума целевой функции внутри
области, заданной ограничениями. Ограничения могут задаваться в форме
равенств и неравенств.
Задача условной оптимизации формулируется следующим образом:
даны дважды непрерывно дифференцируемые целевая функция
)
(
x
I
и
функции ограничений
)
(
x
q
, определённые на множестве
n
RX , требуется
исследовать целевую функцию
)
(
x
I
на экстремумы, т. е. определить точки
X
x
её минимумов и максимумов на
X
:
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных в общем случае равенствами и неравенствами:
,,),1(,0)(
;;,,1,0)(
pmjxq
nmmjxq
xX
j
j
где
m
и
p
— целые числа.
Выражение
n
RX означает, что множество допустимых решений
X
принадлежит множеству действительных чисел
n
R
, где значок
n
соответ-
ствует числу переменных в векторе
T
n
xxxx ),,(
21
. Кроме целевой функ-
ции, дополнительно имеется также
m
условий в виде равенств и
)
(
m
p
условий в виде неравенств, называемых соответственно ограничениями-
равенствами и ограничениями-неравенствами. Функции-ограничения приве-
дены в унифицированной форме, а именно, в их правой части стоят нули, так
как любые равенства и неравенства можно привести к данному виду, перене-
ся все слагаемые из правой части в левую. Кроме того, все неравенства пред-
ставлены в виде нестрогих неравенств типа "меньше или равно", так как в
случае неравенства "больше или равно" его можно привести к данному виду
умножением обеих частей неравенства на коэффициент –1. Ограничения-
неравенства всегда задают нестрогими, т. е. используются знаки "меньше или
равно". Можно показать (см. ниже), что всякое строгое неравенство ("мень-
35
ше") можно свести к нестрогому путём введения новой переменной, отлича-
ющейся от существующей на небольшую величину.
Унификация вида ограничений позволяет упростить формулировку тео-
рем и алгоритмов, никак не сужая область применимости получаемых ре-
зультатов.
При поиске условного экстремума характерным является то, что реше-
ния ищутся не в области всех действительных чисел
n
R
, как это было при
поиске безусловного экстремума (и о чём говорила запись
n
R
x
), а в огра-
ниченной области
n
R
X
допустимых решений, принадлежащей области
n
R
, но не обязательно включающей всю эту область (при этом используется
запись
X
x
, а не
n
R
x
).
Изменение значений вектора
x
может приводить к тому, что некоторые
ограничения-неравенства ("меньше или равно") превращаются в ограниче-
ния-равенства ("равно"). Эти ограничения называют активными. Те ограни-
чения-неравенства, которые остаются неравенствами ("меньше"), называют
пассивными. Активные ограничения-неравенства интересны тем, что в случае
своей активности они пополняют собой совокупность ограничений-равенств.
Активные ограничения-неравенства играют важную роль в некоторых теоре-
мах, связанных с определением экстремумов. Это связано с тем, что физиче-
ски "выход" на равенство означает некие предельные возможности измене-
ния вектора
x
, когда ограничения ещё формально выполняются.
При решении задач на поиск условного экстремума используют специ-
альную функцию — функцию Лагранжа, которую получают из целевой
функции и функций ограничений.
Обобщённая функция Лагранжа:
)()()()()(),,(
221100
xqxqxqxqxIxL
ppmm
p
j
jj
xqxI
1
0
)()(
.
Классическая функция Лагранжа:
)()()()()(),(
2211
xqxqxqxqxIxL
ppmm
p
j
jj
xqxI
1
)()(
.
Функция Лагранжа содержит целевую функцию
)
(
x
I
и сумму всех
функций-ограничений (как равенств, так и неравенств), умноженных на весо-
36
вые коэффициенты (числа)
j
, которые называются множителями Лагран-
жа и могут быть представлены в виде вектора:
T
p
p
,,
21
2
1
,
где
T
— символ транспонирования.
Различие между обобщённой и классической функциями Лагранжа в
том, что в обобщённой функции имеется коэффициент
0
л при целевой функ-
ции, а в классической функции этот коэффициент равен 1. Очевидно, что
можно перейти от классической функции к обобщённой умножением на этот
коэффициент. И наоборот, чтобы перейти от обобщённой функции к класси-
ческой, необходимо поделить обобщённую функцию на этот коэффициент.
Функция Лагранжа заменяет собой целевую функцию при поиске услов-
ного экстремума, т. е. когда при безусловной оптимизации используется це-
левая функция, при условной — часто (хотя и не всегда таким же образом)
используется функция Лагранжа. Поэтому для функции Лагранжа также вво-
дят уже известные понятия градиента и второго дифференциала.
Градиент обобщённой функции Лагранжа:
T
n
n
x
x
xL
x
xL
x
xL
x
xL
x
xL
x
xL
xL
),,(
,,
),,(
,
),,(
),,(
),,(
),,(
),,(
0
2
0
1
0
0
2
0
1
0
0
.
Градиент классической функции Лагранжа:
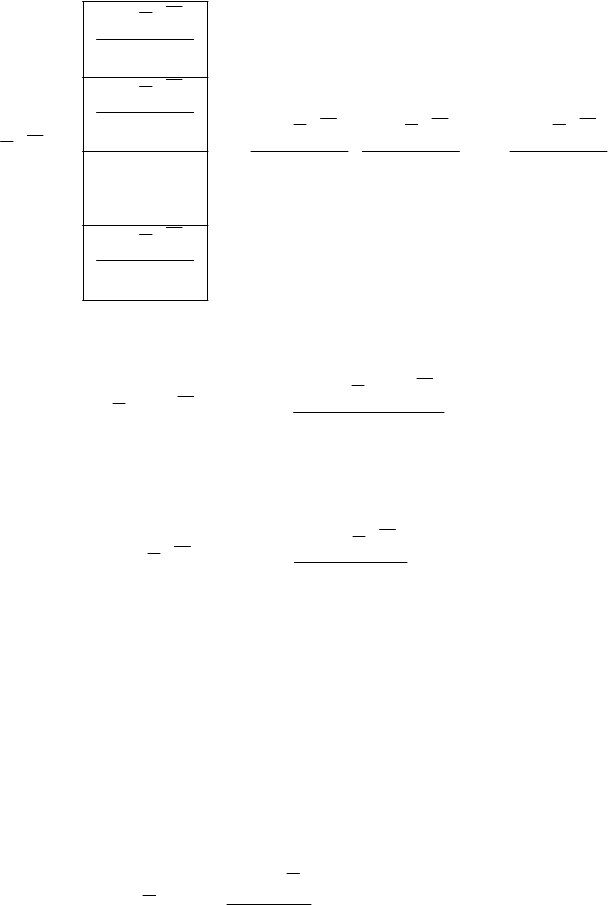
37
T
n
n
x
x
xL
x
xL
x
xL
x
xL
x
xL
x
xL
xL
),(
,,
),(
,
),(
),(
),(
),(
),(
21
2
1
.
Второй дифференциал обобщённой функции Лагранжа:
ji
n
i
n
j
ji
dxdx
xx
xL
xLd
1 1
0
2
0
2
),,(
),,(
.
Второй дифференциал классической функции Лагранжа:
n
j
n
i
ij
ji
dxdx
xx
xL
xLd
1 1
2
2
),(
),(
.
Градиент функции Лагранжа похож на градиент целевой функции, а
второй дифференциал в некотором роде заменяет матрицу Гессе. Действи-
тельно, функция Лагранжа содержит в себе целевую функцию, но имеет в ка-
честве дополнения также выражение, составленное из функций-ограничений.
Кроме этих понятий, используются также первые дифференциалы функ-
ций ограничений:
n
i
i
i
j
j
dx
x
xq
xdq
1
)(
)( ,
p
j
,
,
1
.
Здесь рассматривается
p
ограничений (т. е. все ограничения — и равен-
ства, и неравенства) и каждое из них дифференцируется по всем переменным
i
x . Дифференциал представляет собой сумму всех полученных первых про-
изводных, умноженных на малые приращения соответствующих переменных
i
dx . Число составляющих в каждой сумме равно числу переменных
i
x , т. е.
равно
n
. При этом некоторые составляющие будут равны нулю (для тех
i
x ,
которых нет в данном ограничении). Число полученных выражений для
дифференциалов будет равно числу ограничений, т. е.
p
.
Ниже рассматриваются примеры нахождения приведённых выше выра-
жений.

38
Пример 2.5. Пусть задана целевая функция
2
2
2
1
)( xxxI на множестве
03
1
2
2
xxxX , т. е. задано одно ограничение-равенство
03)(
1
2
21
xxxq , причём здесь
2
n
,
1
m
,
1
p
.
Требуется записать обе функции Лагранжа, найти их градиент и вторые
дифференциалы, а также первый дифференциал функции-ограничения.
Обобщённая функция Лагранжа:
)3()()()(),,(
1
2
21
2
2
2
101100
xxxxxqxIxL
.
Классическая функция Лагранжа:
)3()()()(),(
1
2
21
2
2
2
111
xxxxxqxIxL
.
Градиент обобщённой функции Лагранжа:
2
1
2
21
2
2
2
10
1
1
2
21
2
2
2
10
2
0
1
0
0
)]3()([
)]3()([
),,(
),,(
),,(
x
xxxx
x
xxxx
x
xL
x
xL
xL
x
2120
110
22
2
xx
x
.
Градиент классической функции Лагранжа:
2
1
2
21
2
2
2
1
1
1
2
21
2
2
2
1
2
1
)]3()[(
)]3()[(
),(
),(
),(
x
xxxx
x
xxxx
x
xL
x
xL
xL
x
212
11
22
2
xx
x
.
Второй дифференциал обобщённой функции Лагранжа:
ji
n
i
n
j
ji
dxdx
xx
xL
xLd
1 1
0
2
0
2
),,(
),,(
ji
i j
ji
dxdx
xx
xxxx
2
1
2
1
1
2
21
2
2
2
10
2
)]3()([
=
i
i j
j
ji
dxdx
x
xxxx
x
2
1
2
1
1
2
21
2
2
2
10
)]3()([

39
11
1
1
2
21
2
2
2
10
1
)]3()([
dxdx
x
xxxx
x
12
2
1
2
21
2
2
2
10
1
)]3()([
dxdx
x
xxxx
x
22
2
1
2
21
2
2
2
10
2
)]3()([
dxdx
x
xxxx
x
21
1
1
2
21
2
2
2
10
2
)]3()([
dxdx
x
xxxx
x
122120
1
11110
1
]22[]2[ dxdxxx
x
dxdxx
x
21110
2
222120
2
]2[]22[ dxdxx
x
dxdxxx
x
2
210
2
10
2
210
2
10
)(220)22(02 dxdxdxdx
.
Второй дифференциал классической функции Лагранжа:
ji
n
i
n
j
ji
dxdx
xx
xL
xLd
1 1
0
2
0
2
),,(
),,(
2
21
2
1
)1(22 dxdx
.
Как и следовало ожидать, выражения для классической функции Ла-
гранжа получаются из выражений для обобщённой функции Лагранжа при-
равниванием 1
0
.
Первые дифференциалы для функций-ограничений:
2
2
1
1
2
1
1
)()()()(
)( dx
x
xq
dx
x
xq
dx
x
xq
dx
x
xq
xdq
jj
i
i
i
j
n
i
i
i
j
j
,
1
,
,
1
j
.
2212
2
1
2
2
1
1
1
2
2
1
2
33
)( dxxdxdx
x
xx
dx
x
xx
xdq
.
Если имеются как ограничения-равенства, так и ограничения-
неравенства, то это — задача со смешанными ограничениями. Но в частном
случае могут быть только ограничения-равенства (
0
p
) или только ограни-
чения-неравенства (
m
p
). Все три случая имеют свои особенности, которые
рассматриваются ниже.
Выделяют необходимые и достаточные условия оптимизации, первого и
второго порядка.

40
Необходимые условия оптимизации формулируются в следующем ви-
де: известно, что рассматриваемая точка является точкой экстремума, тогда в
этой точке выполняется ряд условий.
Достаточные условия оптимизации формулируются в следующем виде:
известно, что в рассматриваемой точке выполняется ряд условий, тогда она
является точкой экстремума.
Выделяют также условия первого и второго порядка. В условиях перво-
го порядка используются первые производные и первые дифференциалы, в
условиях второго порядка — вторые производные и вторые дифференциалы.
Таким образом, существует четыре варианта условий существования
экстремума: необходимые условия первого порядка, необходимые условия
второго порядка, достаточные условия первого порядка, достаточные усло-
вия второго порядка.
Необходимые условия служат для нахождения точки, в которой предпо-
ложительно может быть экстремум. Достаточные условия служат для про-
верки, действительно ли в найденной точке имеется экстремум и какой он —
минимум или максимум. Поэтому для решения задачи оптимизации всегда
нужны оба типа условий — как необходимые, так и достаточные. Наличие
условий первого и второго порядков, на первый взгляд, является избыточ-
ным. Но в реальности эти условия несколько различаются. Условия первого
порядка проще, чем второго, хотя бы потому, что целевая функция и ограни-
чения должны быть лишь однократно непрерывно дифференцируемы. Для
применения условий второго порядка требуется двукратная непрерывная
дифференцируемость функций. Поэтому стараются применять условия пер-
вого порядка, но для некоторых задач условия первого порядка не дают од-
нозначного решения и тогда применяют условия второго порядка.
2.3.2 Задача условной оптимизации с ограничениями-равенствами
Постановка задачи условной оптимизации с ограничениями-
равенствами
Даны дважды непрерывно дифференцируемые целевая функция
)
(
x
I
и
функции ограничений
)
(
x
q
, определённые на множестве
n
RX , требуется
исследовать целевую функцию
)
(
x
I
на экстремумы, т. е. определить точки
X
x
её минимумов и максимумов на
X
:
)(min)( xIxI
Xx
, )(max)( xIxI
Xx
с учётом условий, заданных равенствами:
