Бронов С.А. Методы оптимизации в САПР
Подождите немного. Документ загружается.

21
где переменными являются
k
x
Δ
;
k
a и
ki
h
,
— постоянные коэффициенты.
В конечном счёте,
)
(
x
I
после вычислений даёт конкретное число, кото-
рое может быть нулём, положительным или отрицательным.
Матрица Гессе находится обычным образом, а затем в неё подставляют-
ся значения вектора в точке разложения в ряд и таким образом получаются
постоянные коэффициенты
ki
h
,
. В теории оптимизации часто используется
квадратичная форма.
Определение1.1. Квадратичная форма (и соответствующая ей матрица
Гессе) может быть:
положительно определённой, если для любого ненулевого вектора
x
Δ
выполняется неравенство 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
;
отрицательно определённой, если для любого ненулевого вектора
x
Δ
выполняется неравенство 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
;
положительно полуопределённой, если для любого вектора
x
Δ
вы-
полняется неравенство 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
и имеется отличный от
нуля вектор
x
Δ
, для которого 0Δ)(Δ
0
xxx
T
H ;
отрицательно полуопределённой, если для любого ненулевого вектора
x
Δ
выполняется неравенство 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
и имеется отлич-
ный от нуля вектор
x
Δ
, для которого 0Δ)(Δ
0
xxx
T
H ;
неопределённой, если существуют такие векторы
x
Δ
и
x
~
Δ
, для кото-
рых выполняются неравенства 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
и
0
~
Δ)
~
(
~
Δ
0
xxx
T
H ,
0
)
~
(
x
H
;
тождественно равной нулю, если для любого вектора
x
Δ
выполняется
равенства 0Δ)(Δ
0
xxx
T
H ,
0
)
(
x
H
.
1.3 Выпуклые множества и функции
При анализе целевой функции большое значение имеет её характер и
вид экстремумов. Для этого вводится специальные понятия выпуклого мно-
жества и выпуклой функции.
Определение1.2. Множество
n
RX называется выпуклым, если оно
содержит всякий отрезок, концы которого принадлежат
X
, т. е. если для
Xxx
21
, и
1
0
справедливо Xxx
21
)1(
.

22
Пояснения. В данном случае верхние индексы не являются показателями
степени и читаются "икс первый" и "икс второй". Они представляют собой
начало и конец отрезка. Выражение Xxx
21
)1(
показывает движение
при изменении варьируемого параметра
вдоль отрезка от начала отрезка
1
x
(при
1
) к концу отрезка
2
x
(при
0
). При этом все пробегаемые
точки расположены на отрезке прямой [так как выражение
21
)1( xx
есть уравнение прямой] и принадлежат множеству допустимых решений
X
.
Понятие выпуклого (Рисунок 1.3) и невыпуклого (Рисунок 1.4) множе-
ства связано с отсутствием или наличием в нём дефектов: впадин, отверстий,
промежутков и т. п.
1
x
2
x
1
x
2
x
1
x
2
x
Рисунок 1.3 — Выпуклые множества
(не содержат впадин, отверстий, промежутков)
1
x
2
x
1
x
2
x
1
x
2
x
Рисунок 1.4 — Невыпуклые множества
(содержат впадины, отверстия, промежутки)
Очевидно, что выпуклые множества отличаются линейной непрерывно-
стью изменения переменной
x
, значения которой всегда располагаются в
области допустимых решений (заштрихованные области). В случае невыпук-
лых множеств эта область имеет разрыв (или в любом случае, или относи-
тельно линейного изменения переменной
x
). Выпуклые множества относятся
к переменной
x
. Аналогично вводится понятие выпуклой функции, которая
определена на выпуклом множестве
X
, которому принадлежат все
x
.
Определение 1.3. Функция
)
(
x
I
, определённая на выпуклом множестве
X
, называется выпуклой, если справедливо
23
)()1()(])1([
2121
xIxIxxI
для Xxx
21
, ,
21
x
x
и
1
0
.
Пояснения. Здесь предусмотрено, что не может быть случая, когда нача-
ло и конец отрезка совпадают:
21
x
x
, варьируемый параметр
не может
принимать крайние значения 0 и 1, само выражение функции содержит знак
нестрого неравенства ("меньше или равно").
Различают просто выпуклые (в смысле вышеприведённого определе-
ния), строго выпуклые и сильно выпуклые функции.
Определение 1.4. Функция
)
(
x
I
, определённая на выпуклом множестве
X
, называется строго выпуклой, если справедливо
)()1()(])1([
2121
xIxIxxI
для Xxx
21
, ,
21
x
x
и
1
0
.
Пояснения. По сравнению с предыдущим определением, вместо нестро-
го неравенства (меньше или равно) присутствует строгое неравенство (строго
меньше).
Определение1.5. Функция
)
(
x
I
, определённая на выпуклом множестве
X
, называется сильно выпуклой с константой
0
l
, если справедливо
2
212121
)1(
2
)()1()(])1([ xx
l
xIxIxxI
для
Xxx
21
, ,
21
x
x
и
1
0
.
Пояснения. Здесь знак нестрогого неравенства ("меньше или равно") ис-
пользуется как в выражении для функции, так и для определения границ из-
менения варьируемого параметра
. Но, в отличие от определения просто
выпуклой функции, добавляется ещё одно слагаемое, величина которого
определяется квадратом расстояния между начальной и конечной точками
отрезка. При этом степень влияния этого слагаемого определяется величиной
константы
l
, которая не может быть равна нулю.
Выполним сравнение просто выпуклой, строго выпуклой и сильно вы-
пуклой функций.
Понятие выпуклой функции является базовым, поэтому сильно и строго
выпуклые функции одновременно являются просто выпуклыми.
Сильно выпуклая функция одновременно является строго выпуклой.
Физический смысл рассмотренных вариантов выпуклости следующий.
Функцию
)
(
x
I
называют (просто) выпуклой, если она расположена не
выше (применительно к поиску минимума) или не ниже (применительно к
поиску максимума) отрезка, соединяющего две её произвольные точки. Здесь

24
важно, что речь идёт о её произвольных точках, т. е. необходимо перебрать
все возможные сочетания этих точек. Функция может быть на уровне этого
отрезка (используется знак нестрогого неравенства).
Функцию
)
(
x
I
называют строго выпуклой, если она расположена ниже
(применительно к поиску минимума) или выше (применительно к поиску
максимума) отрезка, соединяющего две её произвольные точки. Здесь также
необходимо перебрать все возможные сочетания точек функции. В данном
случае функция не может быть на уровне этого отрезка, так как используется
знак строгого неравенства (отсюда и термин строго выпуклая).
0 5 10 15 20
0
25
50
75
100
1
2
3
4
Рисунок 1.5 — Функции
выпуклые, строго выпуклые и сильно выпуклые
На графике (Рисунок 1.5) представлены три функции (1, 2 и 3) и одни
график прямой (4), относительно которой рассматриваются остальные кри-
вые.
Просто выпуклой функцией являются все приведённые функции, вклю-
чая прямую 4 (как предельный случай). Строго выпуклой функцией являются
функции 1, 2 или 3 (и не может быть 4). Сильно выпуклая функция может
быть 1 — по сравнению с функцией 2 или 2 по сравнению с 3 (понятие силь-
но выпуклой функции — относительное, именно поэтому оно увязывается с
константой
l
, которая характеризует, насколько функция с этой константой
круче, чем без неё).
Характеристика функции может быть получена формально с помощью
матрицы Гессе:
функция
)
(
x
I
выпуклая, если матрица Гессе
0
)
(
x
H
n
R
x
;
функция
)
(
x
I
строго выпуклая, если матрица Гессе
0
)
(
x
H
n
R
x
;
функция
)
(
x
I
сильно выпуклая, если матрица Гессе
E
H
l
x
)
(
(
E
—
единичная матрица)
n
R
x
.
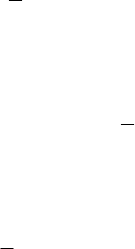
25
Понятия, связанные с матрицей Гессе, рассматриваются ниже.
Характер выпуклости функции используется для поиска экстремумов
(максимумов или минимумов):
если функция
)
(
x
I
выпуклая на выпуклом множестве
X
, то всякая
точка локального минимума (максимума) является точкой её глобального
минимума (максимума) на
X
;
если выпуклая функция
)
(
x
I
достигает своего минимума (максимума)
в двух различных точках, то она достигает минимума (максимума) во всех
точках отрезка, соединяющего эти две точки;
если функция
)
(
x
I
— строго выпуклая на выпуклом множестве
X
, то
она может достигать своего глобального минимума (максимума) на
X
не бо-
лее чем в одной точке.

26
2 Аналитические методы оптимизации
2.1 Необходимые и достаточные условия оптимизации
Выделяют необходимые и достаточные условия оптимизации, первого и
второго порядка.
Необходимые условия оптимизации формулируются в следующем ви-
де: известно, что рассматриваемая точка является точкой экстремума, тогда в
этой точке обязательно выполняется ряд условий, которые называются необ-
ходимыми.
Необходимые условия указывают на возможность (но не обязатель-
ность) наличия экстремума: без выполнения этих условий экстремума точно
нет, но при их выполнении он может быть или не быть.
Достаточные условия оптимизации формулируются в следующем виде:
известно, что в рассматриваемой точке выполняется ряд условий, тогда она
является точкой экстремума.
Достаточные условия указывают на то, что экстремум точно имеется. Но
их невыполнение не гарантирует, что его нет.
Необходимые и достаточные условия оптимизации связаны с первыми и
вторыми производными целевой функции. В случае нескольких переменных
первая производная представляется градиентом, а вторая — матрицей Гессе.
Таким образом, выполнение необходимых условий не гарантирует, что
экстремум есть, а невыполнение достаточных условий — что его нет. Это
можно представить в виде таблицы истинности:
Необход
и
мые
условия
x
Достато
ч
ные
условия
y
Наличие
решения
z
0 0 0
0 1 1
1 0 ×
1 1 1
Здесь знаком × показана неопределённость.
Казалось бы, необходимые условия излишни, и можно всегда пользо-
ваться только достаточными условиями, которые дают гарантию наличия
экстремума. Но оказывается, что на основе необходимых условий получают
систему уравнений (иногда дополненную неравенствами), с помощью кото-
рой находят решение — точку возможного экстремума. Затем с помощью до-
статочных условий подтверждают или опровергают наличие экстремума. Ес-
ли он есть, определяют его вид — максимум или минимум.
Необходимые условия могут быть первого и второго порядка. Необхо-
димые условия первого порядка базируются на градиенте (первые производ-

27
ные), а второго порядка — на градиенте и матрице Гессе (вторые производ-
ные). Кратность дифференцирования и определяет порядок необходимых
условий.
Безусловный экстремум ищется на всём множестве допустимых реше-
ний
n
R
X
(используется знак равенства).
Условный экстремум ищется с учётом наличия ограничений, т. е. когда
область допустимых решений
n
R
X
(отсутствует знак равенства). Ограни-
чения бывают различными: например, решения ищутся только среди целых
числе или только среди положительных или только среди отрицательных и
т. д. Ограничения часто задаются системой равенств или неравенств. С одной
стороны, они могут существенно осложнять поиск экстремума, а с другой —
способствовать этому поиску. Некоторые задачи оптимизации имеют реше-
ние только потому, что включают ограничения.
В процессе решения задачи на поиск экстремума необходимо:
определить, имеются ли вообще точки экстремума, т. е. есть ли смысл
их искать;
определить, в каких точках имеются экстремумы;
классифицировать экстремум в каждой точке (максимум это или ми-
нимум, глобальный или локальный);
вычислить значения целевой функции в точках экстремума.
Самой сложной задачей является определение точек экстремума.
2.2 Необходимые и достаточные условия безусловной оп-
тимизации
Формально постановка задачи безусловной оптимизации следующая:
дана дважды непрерывно дифференцируемая функция
)
(
x
I
, определённая на
множестве
n
R
X
, требуется исследовать функцию
)
(
x
I
на экстремум, т. е.
определить точки
X
x
её минимумов и максимумов на
n
R
:
)(min)( xIxI
n
Rx
, )(max)( xIxI
n
R
x
,
где характерным является то, что решения ищутся в области всех действи-
тельных чисел, о чём говорит запись
n
R
x
, так как областью допустимых
решений является вся область
n
R
(при этом не используется запись
X
x
,
так как запись
n
R
X
уже это подразумевает).
Необходимые условия экстремума первого порядка: пусть
n
R
x
—
точка локального экстремума (минимума или максимума) функции
)
(
x
I
на
28
множестве
n
R
и функция
)
(
x
I
дифференцируема в точке
x
, тогда градиент
функции
)
(
x
I
в точке
x
равен нулю, т. е.
0)(
xI
или в развёрнутой форме:
0
0
0
)(
)(
)(
2
1
n
x
xI
x
xI
x
xI
или 0
n
x
xI
x
xI
x
xI
)(
)(
)(
2
1
.
Точки
x
называются стационарными. Их не называют точками экстре-
мума, так как они могут быть точками перегиба. Все точки экстремума явля-
ются стационарными, но не все стационарные — точками экстремума.
Пояснения. Поскольку используется градиент, то к целевой функции
предъявляются требования только об однократном дифференцировании. В
действительности, в конечном счёте, вместо производных появляются и за-
писываются уравнения — линейные или нелинейные. Поэтому необходимые
условия первого порядка приводят к системе алгебраических уравнений (или,
в случае линейных уравнений — к матричному алгебраическому уравнению),
хотя в исходном виде имеется лишь одна целевая функция, но от многих пе-
ременных. Число уравнений (или размер матрицы) равен числу переменных в
целевой функции, так как именно столько производных содержит градиент.
Поэтому число уравнений всегда равно числу переменных, а потому задача
имеет решение.
Полученное условие можно использовать двояко.
Во-первых, можно решить приведённую систему алгебраических урав-
нений, тогда будут получены точки экстремума, которые называют стацио-
нарными, так как они являются точками перегиба функции и поэтому — точ-
ками равновесия: в точках минимума это — точки устойчивого равновесия, а
в точках максимума — неустойчивого (но для целей оптимизации это не
имеет значения).
Во-вторых, можно подставить в приведённую систему уравнений некий
начальный набор значений
x
и вычислить градиент, который, вероятнее
29
всего, будет отличаться от нуля. Затем следует выбрать новый набор значе-
ний
x
и вновь подставить его в уравнения, вычислить новое значение гра-
диента. Далее следует подбирать
x
таким образом, чтобы значения градиен-
та последовательно приближались к нулю. Создание эффективных алгорит-
мов выбора
x
в зависимости от получаемых промежуточных значений гра-
диента является одной из задач теории оптимизации. Эти алгоритмы должны
обеспечивать постепенный и быстрый переход к нулевому градиенту. В ре-
альности нулевой градиент методом подбора получить почти невозможно,
поэтому обычно речь идёт о незначительных отклонениях от нуля — с точ-
ностью до задаваемой допустимой погрешности.
Пример 1.4. Пусть задана целевая функция от двух аргументов
21
2
2
2
121
35)( xxxxxxxI . Требуется проверить выполнение необходи-
мых условий наличия экстремума. График целевой функции (Рисунок 2.1)
показывает, что эта функция имеет экстремум, а именно — минимум.
Найдём градиент целевой функции:
)6020(
)01001(
)352(
)352(
)(
)(
)(
12
21
2
21
2
2
2
121
1
21
2
2
2
121
2
1
xx
xx
x
xxxxxx
x
xxxxxx
x
xI
x
xI
xI
.
Если приравнять градиент нулю, будет получена система алгебраиче-
ских уравнений:
0
0
62
101
12
21
xx
xx
,
2
1
6
10
21
21
xx
xx
,
;26
;110
21
21
xx
xx
.
Эта система имеет следующее решение:
1) в первом уравнении выражаем
2
x через
1
x :
12
101 xx
;
2) подставляем
2
x во второе уравнение: ;2)101(6
11
xx
3) находим
1
x : 2606
11
xx ; 459
1
x ; 068,0
59
4
1
x ;
4) находим
2
x : 322,0
59
19
59
4059
59
4
101101
12
xx ;
5) находим значение целевой функции в точке
21
, xx =
59
19
,
59
4
:
356
,
0
)
322
,
0
;
068
,
0
(
I
.
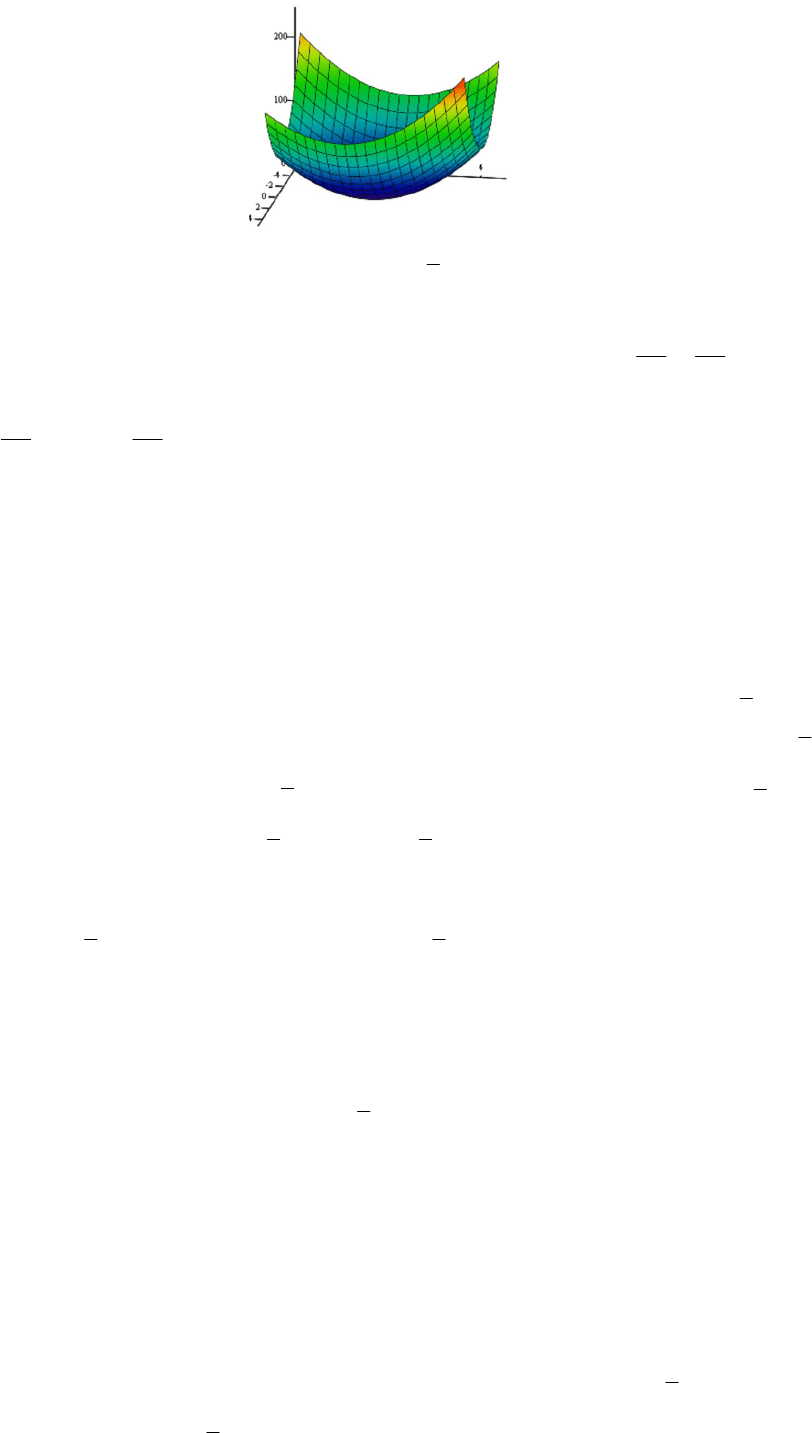
30
Рисунок 2.1 — График функции
21
2
2
2
121
352)( xxxxxxxI
Таким образом, в точке с координатами
2
1
, xx =
59
19
,
59
4
, т. е. при
59
4
1
x ,
59
19
2
x , имеется экстремум целевой функции, но не известно,
максимум это или минимум. В данном случае можно проверить расчётами в
окрестностях найденной точки. При этом можно задать по одному значению
в сторону увеличения и уменьшения относительно найденных
1
x ,
2
x и убе-
диться, что это — минимум, так как все остальные значения целевой функ-
ции будут больше
356
,
0
I
.
Необходимые условия экстремума второго порядка: пусть
n
R
x
—
точка локального экстремума (минимума или максимума) функции
)
(
x
I
на
множестве
n
R
и функция
)
(
x
I
дважды дифференцируема в точке
x
, тогда
матрица Гессе функции
)
(
x
I
в точке
x
является положительно (отрица-
тельно) полуопределённой, т. е.
0)(
xH — для минимума, 0)(
xH — для максимума.
Для применения рассмотренного условия второго порядка необходимо
записать матрицу Гессе, выполнив дифференцирование по всем переменным,
входящим в целевую функцию, а затем подставить в полученные выражения
значения этих переменных в точке
x
(например, в точке, которая подозрева-
ется на экстремум), после чего матрица станет числовой, причём все её эле-
менты будут больше или равны нулю (для минимума) или меньше или равны
нулю (для максимума). Это условие не позволяет определить точку экстре-
мума (как это было в случае с градиентом, который приравнивался нулю и
тем самым появлялась система уравнений, решение которой было точкой
экстремума), а лишь проверить её.
Достаточные условия экстремума: пусть функция
)
(
x
I
дважды диф-
ференцируема в точке
n
R
x
, её градиент равен нулю
