Brizard A. An Introduction to Lagrangian Mechanics

Подождите немного. Документ загружается.

8.2. SMALL OSCILLATIONS ABOUT STABLE EQUILIBRIA 145

which becomes

(ρ)=

µρ

(3 − n). (8.5)

Hence, V

(ρ) is positive if n<3, and thus circular orbits are stable in central-force ﬁelds

F (r)=−kr

−n

if n<3.

8.2 Small Oscillations about Stable Equilibria

Once an equilibrium point x

is shown to be stable, i.e., f

) < 0orV

) > 0, we may

expand x = x

+ δx about the equilibrium point (with δx  x

) to ﬁnd the linearized force

equation

mδ¨x = − V

) δx, (8.6)

which has oscillatory behavior with frequency

ω(x

)

We ﬁrst look at the problem of a bead on a rotating hoop, where the frequency of small

oscillations ω(θ

) is either given in Eq. (8.2) as

ω(0) =

(0)

= ω

√

ν − 1

for θ

= 0 and ν>1, or is given in Eq. (8.3) as

ω(θ

(θ

)

= ω

√

1 − ν

for θ

= arccos(ν) and ν<1.

Next, we look at the frequency of small oscillations about the stable circular orbit in a

central-force ﬁeld F (r)=−kr

−n

(with n<3). Here, from Eq. (8.5), we ﬁnd

ω =

(ρ)

k (3 − n)

µρ

n+1

where `

= µk ρ

3−n

was used. We note that for the Kepler problem (n = 2), the period of

small oscillations T =2π/ω is expressed as

(2π)

which is precisely the statement of Kepler’s Third Law for circular orbits. Hence, a small

perturbation of a stable Keplerian circular orbit does not change its orbital period.

146 CHAPTER 8. NORMAL-MODE ANALYSIS

Figure 8.2: Coupled masses and springs

8.3 Coupled Oscillations and Normal-Mode Analysis

8.3.1 Coupled Simple Harmonic Oscillators

We begin our study of linearily-coupled oscillators by considering the following coupled

system comprised of two block-and-spring systems (with identical mass m and identical

spring constant k) coupled by means of a spring of constant K. The coupled equations are

m ¨x

= −(k + K) x

+ Kx

and m ¨x

= −(k + K) x

+ Kx

. (8.7)

The solutions for x

(t) and x

(t) by following a method known as the normal-mode analysis.

First, we write x

(t) and x

(t) in the normal-mode representation

(t)=x

− iωt

and x

(t)=x

− iωt

, (8.8)

where x

and x

are constants and the eigenfrequency ω is to be solved in terms of the system

parameters (m,k,K). Next, substituting the normal-mode representation into Eq. (8.7),

we obtain the following normal-mode matrix equation

m − (k + K) K

Kω

m − (k + K)

=0. (8.9)

To obtain a non-trivial solution

6=06= x

, the determinant of the matrix in Eq. (8.9) is

required to vanish, which yields the characteristic polynomial

[ω

m − (k + K)]

− K

=0,

whose solutions are the eigenfrequencies

(k + K)

8.3. COUPLED OSCILLATIONS AND NORMAL-MODE ANALYSIS 147

If we insert ω

=(k +2K)/m into the matrix equation (8.9), we ﬁnd

=0,

which implies that x

= −x

, and thus the eigenfrequency ω

is asso ciated with an anti-

symmetric coupled motion. If we insert ω

−

= k/m into the matrix equation (8.9), we

ﬁnd

−KK

K −K

=0,

which implies that

= x

, and thus the eigenfrequency ω

−

is associated with a symmetric

coupled motion.

Lastly, we construct the normal coordinates η

and η

−

, which satisfy the condition

¨η

= −ω

. From the discussion ab ove, we ﬁnd

−

(t)=x

(t)+x

(t) and η

(t)=x

(t) − x

(t). (8.10)

The solutions η

(t) are of the form

= A

cos(ω

t + ϕ

where A

and ϕ

are constants (determined from initial conditions). The general solution

of Eqs. (8.7) can, therefore, be written explicitly in terms of the normal coordinates η

follows

(t)

−

cos(ω

−

t + ϕ

−

) ±

cos(ω

t + ϕ

8.3.2 Nonlinear Coupled Oscillators

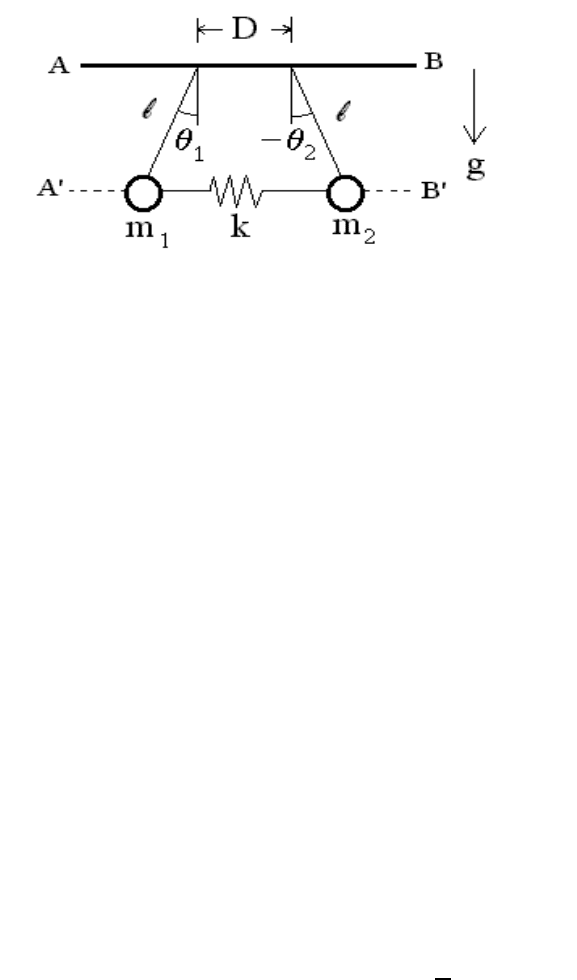
We now consider the following system composed of two pendula of identical length ` but

diﬀerent masses m

and m

coupled by means of a spring of constant k in the presence of

a gravitational ﬁeld of constant acceleration g. (The distance D between the two p oints

of attach of the pendula is equal to the length of the spring in its relaxed state and we

assume, for simplicity, that the masses always stay on the same horizontal line.) Using the

generalized coordinates ( θ

,θ

) deﬁned in the Figure above, the Lagrangian for this system

L =



+ m



− g` { m

(1 − cos θ

)+m

(1 − cos θ

) }

−

(sin θ

− sin θ

)

and the nonlinear coupled equations of motion are

= − m

sin θ

− k (sin θ

− sin θ

) cos θ

= − m

sin θ

+ k (sin θ

− sin θ

) cos θ

148 CHAPTER 8. NORMAL-MODE ANALYSIS

Figure 8.3: Coupled pendula

where ω

= g/`.

It is quite clear that the equilibrium point is θ

=0=θ

and expansion of the coupled

equations about this equilibrium yields the coupled linear equations

¨q

= − m

− k ( q

−q

¨q

= − m

+ k ( q

− q

where θ

= q

 1 and θ

= q

 1. The normal-mode matrix associated with these

coupled linear equations is

(ω

− ω

) m

− kk

k (ω

− ω

) m

− k

=0,

and the characteristic p olynomial is

(ω

− ω

) µ − k

(ω

−ω

)=0,

where µ = m

/M is the reduced mass for the system and M = m

+ m

is the total

mass. The eigenfrequencies are thus

−

= ω

and ω

= ω

The normal coordinates η

are expressed in terms of (q

)asη

= a

, where

and b

are constant coeﬃcients determined from the condition ¨η

= −ω

. From

8.3. COUPLED OSCILLATIONS AND NORMAL-MODE ANALYSIS 149

this condition we ﬁnd

+ ω

−

= ω

+ ω

−

For the eigenfrequency ω

−

= ω

, we ﬁnd b

−

= m

, and thus we may choose

−

which represents the center of mass position for the system. For the eigenfrequency ω

+ k/µ, we ﬁnd b

= −1, and thus we may choose

= q

− q

Lastly, we may solve for q

and q

= η

−

and q

= η

−

where η

= A

cos(ω

t + ϕ

) are general solutions of the normal-mode equations ¨η

−ω

150 CHAPTER 8. NORMAL-MODE ANALYSIS

8.4 Problems

Problem 1

The following compound pendulum is composed of two identical masses m attached

by massless rods of identical length ` to a ring of mass M, which is allowed to slide up

and down along a vertical axis in a gravitational ﬁeld with constant g. The entire system

rotates ab out the vertical axis with an azimuthal angular frequency ω

(a) Show that the Lagrangian for the system can be written as

L(θ,

θ)=`



m +2M sin



+ m`

sin

θ +2(m + M)g` cos θ

(b) Identify the equilibrium points for the system and investigate their stability.

in Part (b).

8.4. PROBLEMS 151

Problem 2

Consider the same problem as in Sec. (8.3.1) but now with diﬀerent masses (m

6= m

Calculate the eigenfrequencies and eigenvectors (normal co ordinates) for this system.

Problem 3

Find the eigenfrequencies associated with small oscillations of the system shown below.

Problem 4

Two blocks of identical mass m are attached by massless springs (with identical spring

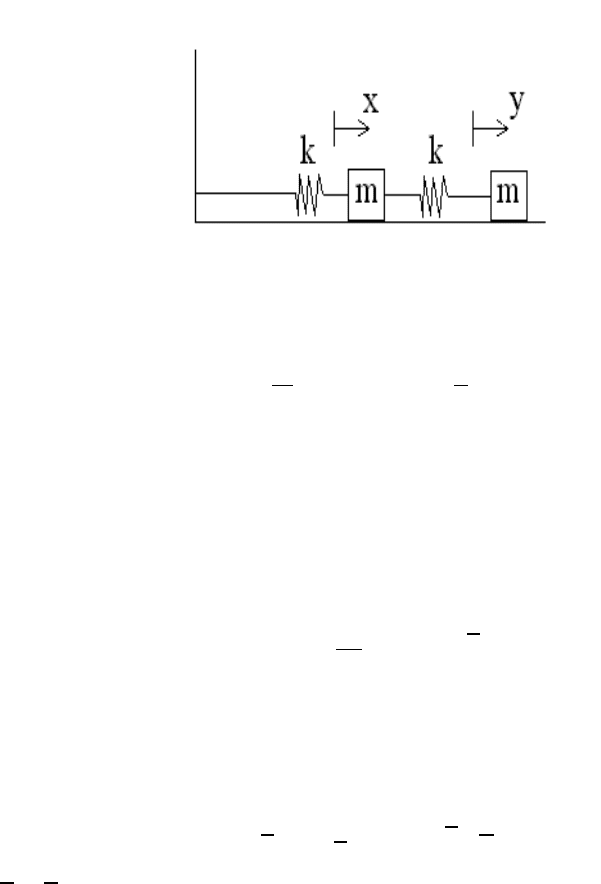
152 CHAPTER 8. NORMAL-MODE ANALYSIS

constant k) as shown in the Figure below.

The Lagrangian for this system is

L(x, ˙x; y, ˙y)=



˙x

+˙y



−

+(y − x)

where x and y denote departures from equilibrium.

(a) Derive the Euler-Lagrange equations for x and y.

(b) Show that the eigenfrequencies for small oscillations for this system are



3 ±

√



where ω

= k/m.

are represented by

the relations



1 ∓

√



where (x

, y

) represent the normal-mode amplitudes.

Problem 5

An inﬁnite sheet with surface mass density σ has a hole of radius R cut into it. A

particle of mass m sits (in equilibrium) at the center of the circle. Assuming that the

8.4. PROBLEMS 153

sheet lies on the (x, y)-plane (with the hole centered at the origin) and that the particle

is displaced by a small amount z  R along the z-axis, calculate the frequency of small

oscillations.

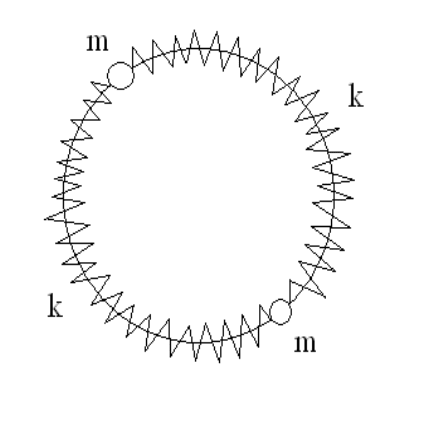
Problem 6

Two identical masses are connected by two identical massless springs and are con-

strained to move on a circle (see Figure below). Of course, the two masses are in equilibrium

when they are diametrically opposite points on the circle.

Solve for the normal modes of the system.

154 CHAPTER 8. NORMAL-MODE ANALYSIS