Brizard A. An Introduction to Lagrangian Mechanics

Подождите немного. Документ загружается.

7.2. ANGULAR MOMENTUM 125

which are known as the Euler equations. Lastly, we note that the rate of change of the

rotational kinetic energy (7.7) is expressed as

rot

= ω · I ·

ω = ω · (−ω × L + N)=N · ω. (7.26)

We note that in the absence of external torque (N = 0), not only is kinetic energy conserved

but also L

i=1

)

, as can be veriﬁed from Eq. (7.25). Note that, for a general

function F (L) of angular momentum and in the absence of external torque, we ﬁnd

= − L ·

∂F

∂L

∂K

rot

∂L

= −

∂F

∂L

· ω × L,

and thus any function of |L| is a constant of the motion for rigid body dynamics.

7.2.2 Euler Equations for a Force-Free Symmetric Top

As an application of the Euler equations (7.25) we consider the case of the dynamics of

a force-free symmetric top, for which N = 0 and I

= I

6= I

. Accordingly, the Euler

equations (7.25) become

˙ω

= ω

− I

)

˙ω

= ω

− I

)

˙ω











, (7.27)

The last Euler equation states that if I

6= 0, we have ˙ω

= 0 or that ω

is a constant of

motion. Next, after deﬁning the precession frequency

= ω



− 1



, (7.28)

which may be positive (I

) or negative (I

), the ﬁrst two Euler equations yield

˙ω

(t)=− ω

(t) and ˙ω

(t)=ω

(t). (7.29)

The general solutions for ω

(t) and ω

(t) are

(t)=ω

cos(ω

t + φ

) and ω

(t)=ω

sin(ω

t + φ

), (7.30)

where ω

is a constant and φ

is an initial phase associated with initial conditions for ω

(t)

and ω

(t). Since ω

and ω

= ω

(t)+ω

(t) are constant, then the magnitude of the angular

velocity ω,

ω =

+ ω

is also a constant. Thus the angle α between ω and

is constant, with

= ω cos α and

+ ω

= ω

= ω sin α.

126 CHAPTER 7. RIGID BODY MOTION

Figure 7.6: Bo dy cone

Since the magnitude of ω is also constant, the ω-dynamics simply involves a constant

rotation with frequency ω

and a precession motion of ω about the

-axis with a precession

frequency ω

; as a result of precession, the vector ω spans the body cone with ω

> 0if

(for a pancake-shaped or oblate symmetric top) or ω

< 0ifI

(for a cigar-

shaped or prolate symmetric top).

For example, to a good approximation, Earth is an oblate spheroid with



+ c



= I

and I

where 2 c =12, 714 km is the Pole-to-Pole distance and 2 a =12, 756 km is the equatorial

diameter, so that

− 1=

− c

+ c

=0.003298... = .

The precession frequency (7.28) of the rotation axis of Earth is, therefore, ω

= ω

, where

=2π rad/day is the rotation frequency of the Earth, so that the precession motion

repeats itself every 

−1

days or 303 days; the actual p eriod is 430 days and the diﬀerence is

partially due to the non-rigidity of Earth and the fact that the Earth is not a pure oblate

spheroid. A slower precession motion of approximately 26,000 years is intro duced by the

combined gravitational eﬀect of the Sun and the Mo on on one hand, and the fact that

the Earth’s rotation axis is at an angle 23.5

to the Ecliptic plane (on which most planets

move).

The fact that the symmetric top is force-free implies that its rotational kinetic energy

is constant [see Eq. (7.26)] and, hence, L · ω is constant while ω × L ·

= 0 according to

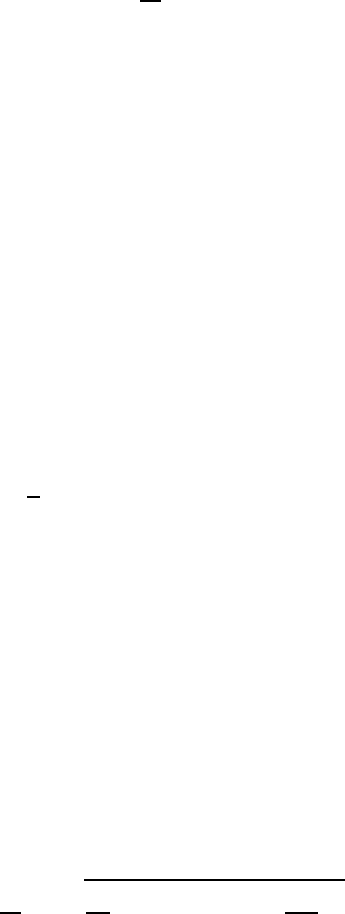
7.2. ANGULAR MOMENTUM 127

Eq. (7.24). Since L itself is constant in magnitude and direction in the LAB (or ﬁxed)

frame, we may choose the

z-axis to be along L (i.e., L = `

z). If at a given instant, ω

=0,

then ω

= ω

= ω sin α and ω

= ω cos α. Likewise, we may write L

= I

= 0, and

= I

ω sin α = ` sin θ,

= I

ω cos α = ` cos θ,

where L · ω = `ω cos θ, with θ represents the space-cone angle. From these equations, we

ﬁnd the relation between the body-cone angle α and the space-cone angle θ to be

tan θ =





tan α, (7.31)

which shows that θ>αfor I

and θ<αfor I

7.2.3 Euler Equations for a Force-Free Asymmetric Top

We now consider the general case of an asymmetric top moving under force-free conditions.

To facilitate our discussion, we assume that I

and thus Euler’s equations (7.25)

for a force-free asymmetric top are

˙ω

= ω

− I

)

˙ω

= − ω

− I

)

˙ω

= ω

− I

)











. (7.32)

As previously mentioned, the Euler equations (7.32) have two constants of the motion:

kinetic energy

K =



+ I



, (7.33)

and the squared magnitude of the angular momentum

= I

+ I

. (7.34)

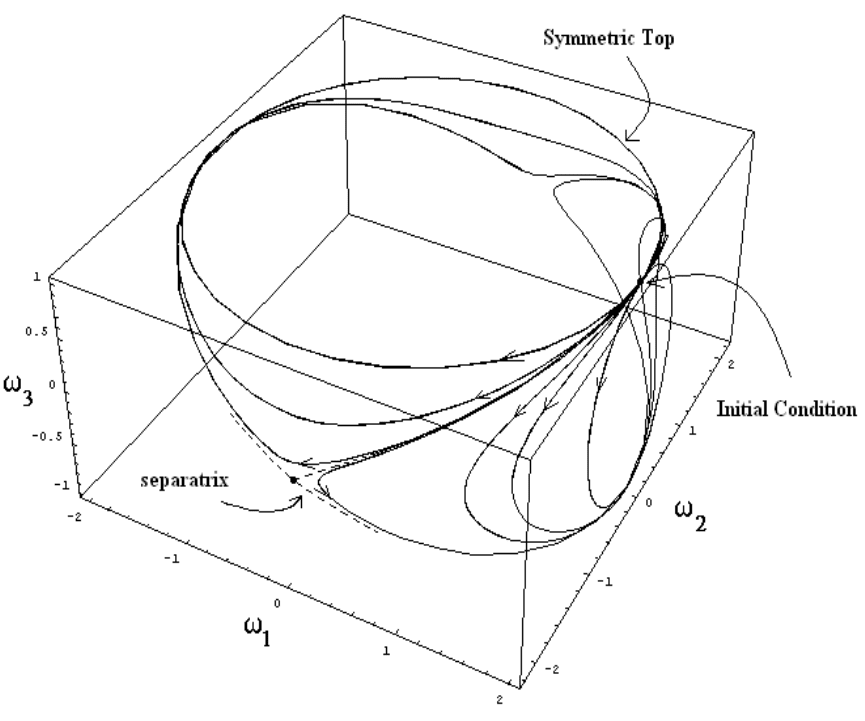
Figure 7.7 shows the numerical solution of the Euler equations (7.32) subject to the

initial condition (ω

,ω

)=(2, 0, 1) for diﬀerent values of the ratios I

and I

Note that in the limit I

= I

(corresp onding to a symmetric top), the top evolves solely

on the (ω

,ω

)-plane at constant ω

.AsI

increases from I

, the asymmetric top exhibits

doubly-periodic behavior in the full (ω

,ω

)-space until the motion becomes restricted to

the (ω

,ω

)-plane in the limit I

 I

. One also clearly notes the existence of a separatrix

which appears as I

reaches the critical value

+ I

− I

)





128 CHAPTER 7. RIGID BODY MOTION

Figure 7.7: Orbits of an asymmetric top

7.2. ANGULAR MOMENTUM 129

at constant I

and I

and given initial conditions (ω

,ω

We note that the existence of two constants of the motion, Eqs. (7.33) and (7.34), for

the three Euler equations (7.32) means that we may express the Euler equations in terms

of a single equation. For this purpose, we introduce the constants

σ =2I

K − L

and ρ = L

− 2 I

from which we obtain expressions for ω

(taken here to be negative) and ω

in terms of ω

= −

ρ − I

− I

) ω

−I

)

and ω

σ − I

− I

) ω

− I

)

. (7.35)

When we substitute these expressions in the Euler equation for ω

, we easily obtain

˙ω

= α

(Ω

− ω

)(Ω

− ω

), (7.36)

where α is a positive dimensionless constant deﬁned as

α =



1 −



− 1



while the constant frequencies Ω

and Ω

are deﬁned as

Ω

2 I

K − L

− I

)

and Ω

− 2 I

−I

)

We immediately note that the evolution of ω

is characterized by the two frequencies Ω

and Ω

, which also represent the turning points at which ˙ω

vanishes. Next, by introducing

a dimensionless frequency u = ω

/Ω

(here, we assume that Ω

≥ Ω

) and a dimensionless

time τ = αΩ

t, the Euler equation (7.36) can now be integrated to yield

τ =

(1 − s

)(1− k

)

Θ(u)

dθ

√

1 − k

sin

, (7.37)

where k

=Ω

/Ω

≥ 1, Θ(u) = arcsin u, and we assume that ω

(t = 0) = 0; compare

Eq. (7.37) with Eq. (3.25).

Lastly, the turning points for ω

are now represented in terms of turning p oints for u

as ω

=Ω

→ u = 1 and ω

=Ω

→ u = k

−1

=Ω

/Ω

≤ 1. Lastly, note that

the separatrix solution of the force-free asymmetric top (see Figure 7.7) corresp onding to

= I

is associated with k = 1 (i.e., Ω

=Ω

130 CHAPTER 7. RIGID BODY MOTION

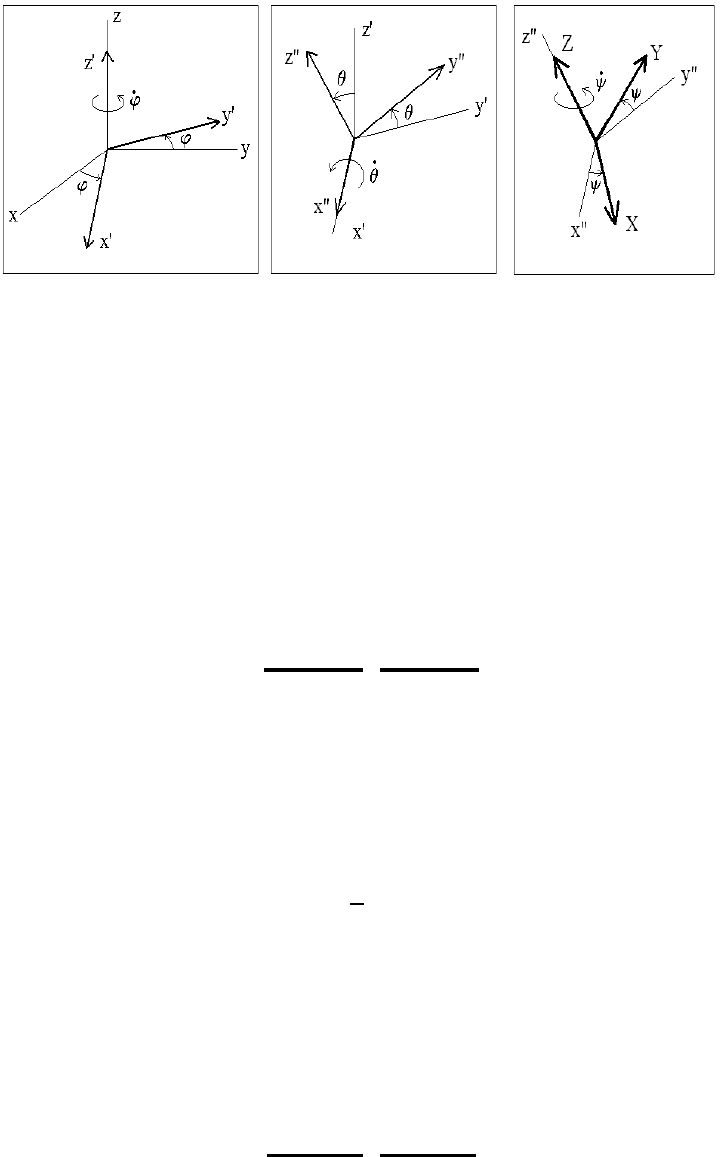
Figure 7.8: Euler angles

7.3 Symmetric Top with One Fixed Point

7.3.1 Eulerian Angles as generalized Lagrangian Coordinates

To describe the physical state of a rotating object with principal moments of inertia

), we need the three Eulerian angles (ϕ, θ, ψ) in the body frame of reference (see

Figure 7.8). The Eulerian angle ϕ is associated with the rotation of the ﬁxed-frame unit

vectors (

z) about the z-axis. We thus obtain the new unit vectors (

) deﬁned as













= R

(ϕ)

z }| {







cos ϕ sin ϕ 0

− sin ϕ cos ϕ 0

001



















(7.38)

The rotation matrix R

(ϕ) has the following prop erties asso ciated with a general rotation

matrix R

(α), where a rotation of axes about the x

-axis is performed through an arbitrary

angle α. First, the matrix R

(−α) is the inverse matrix of R

(α), i.e.,

(−α) · R

(α)=1 = R

(α) · R

(−α).

Next, the determinant of R

(α)is

Det[R

(α)] = + 1.

Lastly, the eigenvalues of R

(α) are + 1, e

iα

, and e

− iα

The Eulerian angle θ is associated with the rotation of the unit vectors (

) about

the x

-axis. We thus obtain the new unit vectors (

) deﬁned as













= R

(θ)

z }| {







10 0

0 cos θ sin θ

0 − sin θ cos θ



















(7.39)

7.3. SYMMETRIC TOP WITH ONE FIXED POINT 131

The Eulerian angle ψ is associated with the rotation of the unit vectors (

) about

the z

-axis. We thus obtain the body-frame unit vectors (

) deﬁned as













= R

(ψ)

z }| {







cos ψ sin ψ 0

− sin ψ cos ψ 0

001



















(7.40)

Hence, the relation between the ﬁxed-frame unit vectors (

z) and the body-frame

unit vectors (

) involves the matrix R = R

(ψ) ·R

(θ) ·R

(ϕ), such that

= R

= cos ψ

⊥ + sin ψ (cos θ

ϕ + sin θ

= − sin ψ

⊥ + cos ψ (cos θ

ϕ + sin θ

= − sin θ

ϕ + cos θ











, (7.41)

where

ϕ = − sin ϕ

x + cos ϕ

y and

⊥ = cos ϕ

x + sin ϕ

y =

ϕ ×

7.3.2 Angular Velocity in terms of Eulerian Angles

The angular velocity ω represented in the three Figures above is expressed as

ω =˙ϕ

z +

The unit vectors

z and

are written in terms of the body-frame unit vectors (

)as

z = sin θ (sin ψ

+ cos ψ

)+cosθ

= cos ψ

− sin ψ

The angular velocity can, therefore, be written exclusively in the body frame of reference

in terms of the Euler basis vectors (7.41) as

ω = ω

+ ω

, (7.42)

where the b ody-frame angular frequencies are

=˙ϕ sin θ sin ψ +

θ cos ψ

=˙ϕ sin θ cos ψ −

θ sin ψ

ψ +˙ϕ cos θ











. (7.43)

Note that all three frequencies are independent of ϕ (i.e., ∂ω

/∂ϕ = 0), while derivatives

with respect to ψ and

ψ are

∂ω

∂ψ

= ω

∂ω

∂ψ

= −ω

, and

∂ω

∂ψ

=0,

132 CHAPTER 7. RIGID BODY MOTION

and

∂ω

∂

=0=

∂ω

∂

and

∂ω

∂

=1.

The relations (7.43) can be inverted to yield

˙ϕ = csc θ (sin ψω

+ cos ψω

θ = cos ψω

− sin ψω

ψ = ω

− cot θ (sin ψω

+ cos ψω

7.3.3 Rotational Kinetic Energy of a Symmetric Top

The rotational kinetic energy (7.7) for a symmetric top can be written as

rot

+ I



+ ω

o

or explicitly in terms of the Eulerian angles (ϕ, θ, ψ) and their time derivatives ( ˙ϕ,

θ,

ψ)as

rot





ψ +˙ϕ cos θ



+ I



+˙ϕ

sin





. (7.44)

We now brieﬂy return to the case of the force-free symmetric top for which the Lagrangian

is simply L(θ,

θ;˙ϕ,

ψ)=K

rot

. Since ϕ and ψ are ignorable coordinates, i.e., the force-free

Lagrangian (7.44) is independent of ϕ and ψ, their canonical angular momenta

∂L

∂ ˙ϕ

= I

(

ψ +˙ϕ cos θ) cos θ + I

sin

θ ˙ϕ, (7.45)

∂L

∂

= I

(

ψ +˙ϕ cos θ)=I

(7.46)

are constants of the motion. By inverting these relations, we obtain

˙ϕ =

− p

cos θ

sin

and

ψ = ω

−

−p

cos θ) cos θ

sin

, (7.47)

and the rotational kinetic energy (7.44) becomes

rot

(

+ I

− p

cos θ)

sin

)

. (7.48)

The motion of a force-free symmetric top can now be described in terms of solutions of the

Euler-Lagrange equation for the Eulerian angle θ:

∂L

∂

= I

θ =

∂L

∂θ

=˙ϕ sin θ (I

cos θ ˙ϕ − p

)

= −

− p

cos θ)

sin θ

− p

cos θ)

sin

. (7.49)

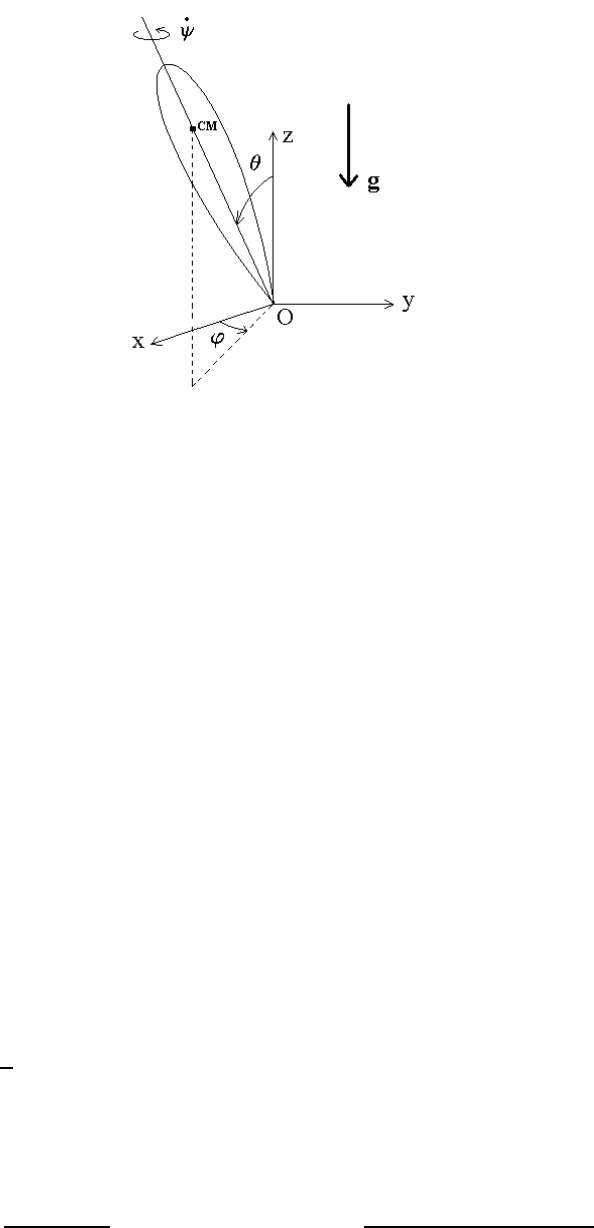
7.3. SYMMETRIC TOP WITH ONE FIXED POINT 133

Figure 7.9: Symmetric top with one ﬁxed point

Once θ( t) is solved for given values of the principal moments of inertia I

= I

and I

and the invariant canonical angular momenta p

and p

, the functions ϕ(t) and ψ(t) are

determined from the time integration of Eqs. (7.47).

7.3.4 Lagrangian Dynamics of a Symmetric Top with One Fixed

Point

We now consider the case of a spinning symmetric top of mass M and principal moments of

inertia (I

= I

6= I

) with one ﬁxed point O moving in a gravitational ﬁeld with constant

acceleration g. The rotational kinetic energy of the symmetric top is given by Eq. (7.44)

while the potential energy for the case of a symmetric top with one ﬁxed point is

U(θ)=Mgh cos θ, (7.50)

where h is the distance from the ﬁxed point O and the center of mass (CM) of the symmetric

top. The Lagrangian for the symmetric top with one ﬁxed point is

L(θ,

θ;˙ϕ,

ψ)=





ψ +˙ϕ cos θ



+ I



+˙ϕ

sin





− Mgh cos θ. (7.51)

A normalized form of the Euler equations for the symmetric top with one ﬁxed point (also

known as the heavy symmetric top) is expressed as

(b − cos θ)

sin

and θ

= a sin θ +

(1 − b cos θ)(b − cos θ)

sin

, (7.52)

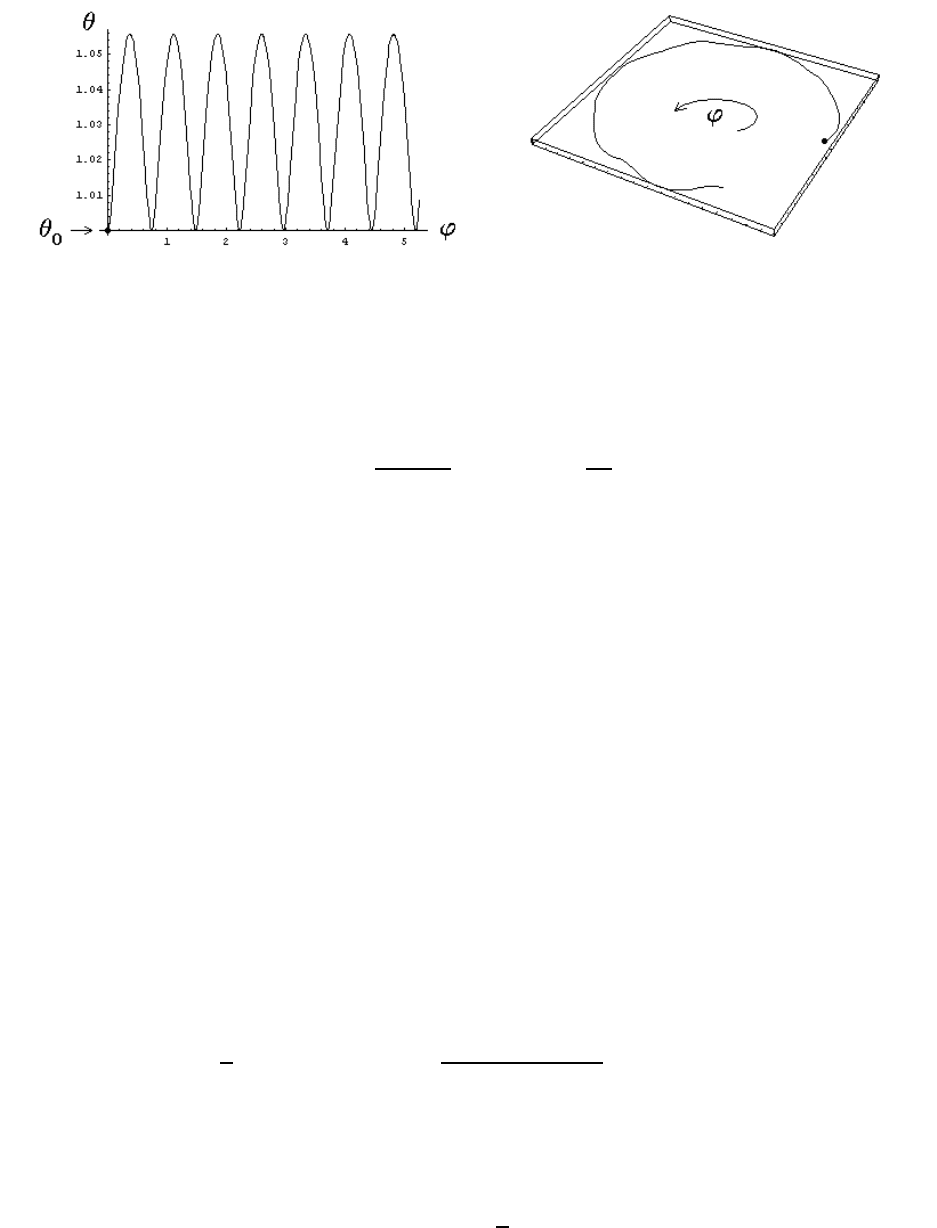
134 CHAPTER 7. RIGID BODY MOTION

Figure 7.10: Orbits of heavy top – Case I

where time has been rescaled such that (···)

=(I

)(···)

and the two parameters a

and b are deﬁned as

a =

MghI

and b =

The normalized heavy-top equations (7.52) have been integrated for the initial con-

ditions (θ

,θ

; ϕ

)=(1.0, 0.0; 0.0). The three Figures shown below correspond to three

diﬀerent cases (I, II, and III) for ﬁxed value of a (here, a =0.1), which exhibit the pos-

sibility of azimuthal reversal when ϕ

changes sign for diﬀerent values of b = p

; the

azimuthal precession motion is called nutation.

The Figures on the left show the normalized heavy-top solutions in the (ϕ, θ)-plane

while the Figures on the right show the spherical projection of the normalized heavy-top

solutions (θ, ϕ) → (sin θ cos ϕ, sin θ sin ϕ, cos θ), where the initial condition is denoted

byadot(•). In Case I (b>cos θ

), the azimuthal velocity ϕ

never changes sign and

azimuthal precession occurs monotonically. In Case II (b = cos θ

), the azimuthal velocity

vanishes at θ = θ

(where θ

also vanishes) and the heavy symmetric top exhibits a cusp

at θ = θ

. In Case III (b<cos θ

), the azimuthal velocity ϕ

vanishes for θ>θ

and the

heavy symmetric top exhibits a phase of retrograde motion. Since the Lagrangian (7.51)

is independent of the Eulerian angles ϕ and ψ, the canonical angular momenta p

and p

resp ectively, are constants of the motion. The solution for θ(t) is then most easily obtained

by considering the energy equation

E =

(

+ I

− p

cos θ)

sin

)

+ Mgh cos θ, (7.53)

where p

and p

= I

are constants of the motion. Since the total energy E is itself a

constant of the motion, we may deﬁne a new energy constant

= E −