Brizard A. An Introduction to Lagrangian Mechanics

Подождите немного. Документ загружается.

5.6. HARD-SPHERE AND SOFT-SPHERE SCATTERING 95

Figure 5.6: Hard-sphere scattering geometry

5.6.1 Hard-Sphere Scattering

We begin by considering the collision of a point-like particle of mass m

with a hard sphere

of mass m

and radius R. In this particular case, the central potential for the hard sphere

U(r)=











∞ (for r<R)

0 (for r>R)

and the collision is shown in Figure 5.6. From Figure 5.6, we see that the impact parameter

b = R sin χ, (5.28)

where χ is the angle of incidence. The angle of reﬂection η is diﬀerent from the angle of

incidence χ for the case of arbitrary mass ratio α = m

. To show this, we decompose

the velocities in terms of components p erpendicular and tangential to the surface of the

sphere at the point of impact, i.e., we respectively ﬁnd

αu cos χ = v

− αv

cos η

αu sin χ = αv

sin η.

From these expressions we obtain

tan η =

αu sin χ

−αu cos χ

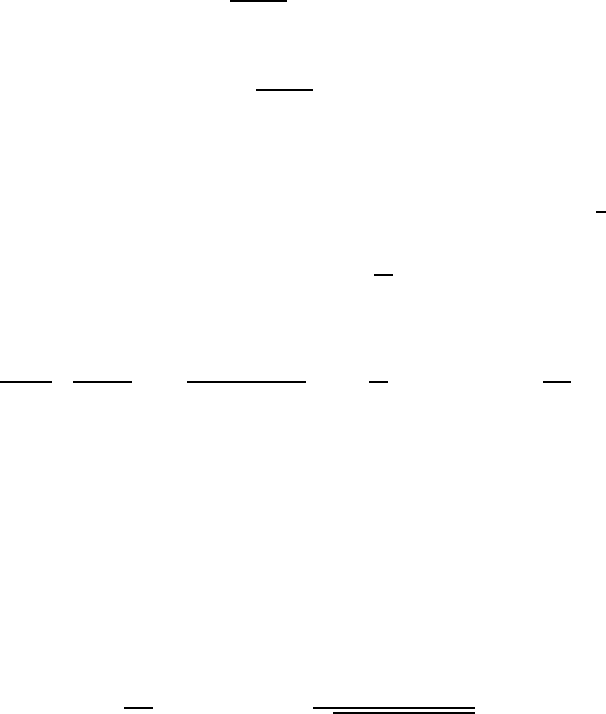
96 CHAPTER 5. COLLISIONS AND SCATTERING THEORY

From Figure 5.6, we also ﬁnd the deﬂection angle θ = π − (χ + η) and the recoil angle

ϕ = χ and thus, according to Chap. 5,



2 α

1+α



u cos χ,

and thus

tan η =



1+α

1 − α



tan χ. (5.29)

We, therefore, easily see that η = χ (the standard form of the Law of Reﬂection) only if

α = 0 (i.e., the target particle is inﬁnitely massive).

In the CM frame, the collision is symmetric with a deﬂection angle χ =

(π − Θ), so

that

b = R sin χ = R cos

The scattering cross section in the CM frame is

(Θ) =

b(Θ)

sin Θ



db(Θ)

dΘ



R cos(Θ/2)

sin Θ



−

sin(Θ/2)



, (5.30)

and the total cross section is

=2π

(Θ) sin Θ dΘ=πR

, (5.31)

i.e., the total cross section for the problem of hard-sphere collision is equal to the eﬀective

area of the sphere.

The scattering cross section in the LAB frame can also be obtained for the case α<1

using Eqs. (5.17) and (5.22) as

σ(θ)=

2 α cos θ +

1+α

cos 2θ

√

1 − α

sin

, (5.32)

for α = m

< 1. The integration of this formula must yield the total cross section

=2π

σ(θ) sin θdθ,

where θ

max

= π for α<1.

5.6.2 Soft-Sphere Scattering

We now consider the scattering of a particle subjected to the attractive potential considered

in Sec. 4.5

U(r)=











− U

(for r<R)

0 (for r>R

(5.33)

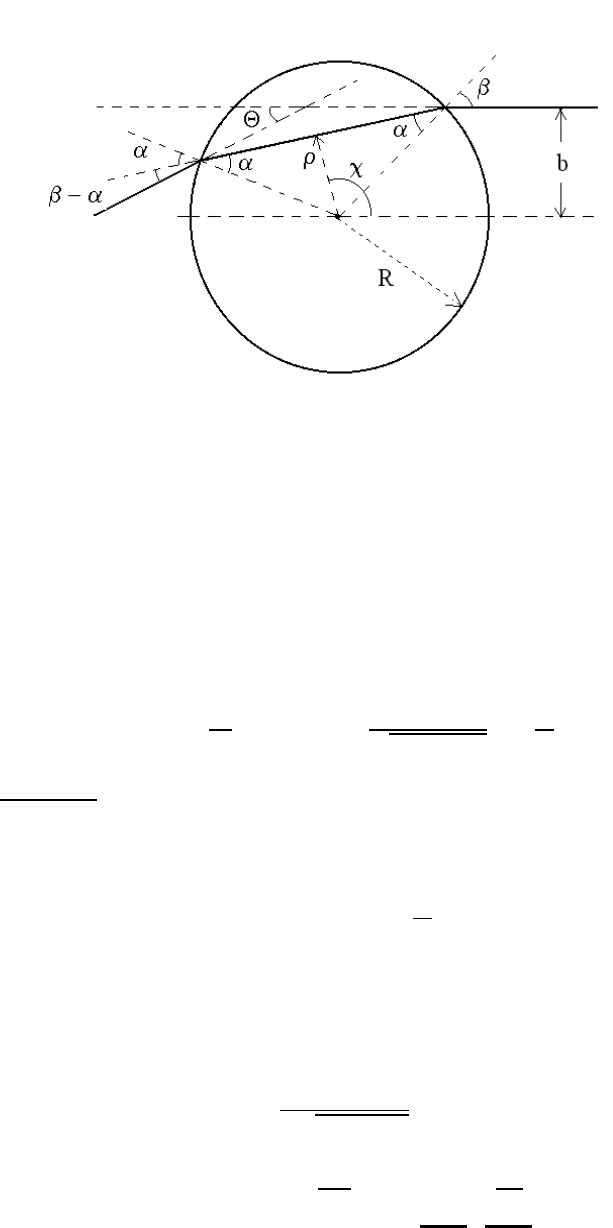
5.6. HARD-SPHERE AND SOFT-SPHERE SCATTERING 97

Figure 5.7: Soft-sphere scattering geometry

where the constant U

denotes the depth of the attractive potential well and E>`

/2µR

involves a single turning point. We denote β the angle at which the incoming particle enters

the soft-sphere potential (see Figure 5.7), and thus the impact parameter b of the incoming

particle is b = R sin β. The particle enters the soft-sphere potential region (r<R) and

reaches a distance of closest approach ρ, deﬁned from the turning-point condition

E = −U

+ E

→ ρ =

1+U

sin β,

where n =

1+U

/E denotes the index of refraction of the soft-sphere potential region.

From Figure 5.7, we note that an optical analogy helps us determine that, through Snell’s

law, we ﬁnd

sin β = n sin



β −



, (5.34)

where the transmission angle α is given in terms of the incident angle β and the CM

scattering angle −ΘasΘ=2(β − α).

The distance of closest approach is reached at an angle χ is determined as

χ = β +

bdr

√

− b

= β + arccos

− arccos

nρ

| {z }

98 CHAPTER 5. COLLISIONS AND SCATTERING THEORY

= β + arccos

(π +Θ), (5.35)

and, thus, the impact parameter b(Θ) can be expressed as

b(Θ) = nR sin



β(b) −



→ b(Θ) =

nR sin(Θ/2)

1+n

− 2n cos(Θ/2)

, (5.36)

and its derivative with respect to Θ yields

dΘ

[n cos(Θ/2) − 1] [n − cos(Θ/2)]

[1 + n

− 2n cos(Θ/2)]

3/2

and the scattering cross section in the CM frame is

(Θ) =

b(Θ)

sin Θ



db(Θ)

dΘ



|[n cos(Θ/2) −1] [n − cos(Θ/2)]|

cos(Θ/2) [1 + n

− 2n cos(Θ/2)]

Note that, on the one hand, when β =0,weﬁndχ = π/2andΘ

min

= 0, while on the other

hand, when β = π/2, we ﬁnd b = R and

1=n sin



−

max



= n cos(Θ

max

/2) → Θ

max

= 2 arccos



−1



Moreover, when Θ = Θ

max

, we ﬁnd that db/dΘ vanishes and, therefore, the diﬀerential

cross section vanishes σ

(Θ

max

) = 0, while at Θ = 0, we ﬁnd σ

(0) = [n/(n − 1)]

/4).

Figure 5.8 shows the soft-sphere scattering cross section σ(Θ) (normalized to the hard-

sphere cross section R

/4) as a function of Θ for four cases: n =(1.1, 1.15) in the soft-sphere

limit (n → 1) and n = (50, 1000) in the hard-sphere limit (n →∞). We clearly see the

strong forward-scattering behavior as n → 1 (or U

→ 0) in the soft-sphere limit and the

hard-sphere limit σ → 1asn →∞. We note that the total scattering cross section (using

the substitution x = n cos Θ/2)

=2π

max

(Θ) sin Θ dΘ=2πR

(x − 1) (n

− x) dx

(1 + n

− 2x)

= πR

is independent of the index of refraction n and equals the hard-sphere total cross section

(5.31).

The opposite case of a repulsive soft-sphere p otential, where −U

is replaced with U

Eq. (5.33), is treated by replacing n =(1+U

/E)

with n =(1−U

/E)

−

and Eq. (5.36)

is replaced with

b(Θ) = n

−1

R sin



β(b)+



→ b(Θ) =

R sin(Θ/2)

1+n

− 2n cos(Θ/2)

, (5.37)

while Snell’s law (5.34) is replaced with

sin



β +



= n sin β.

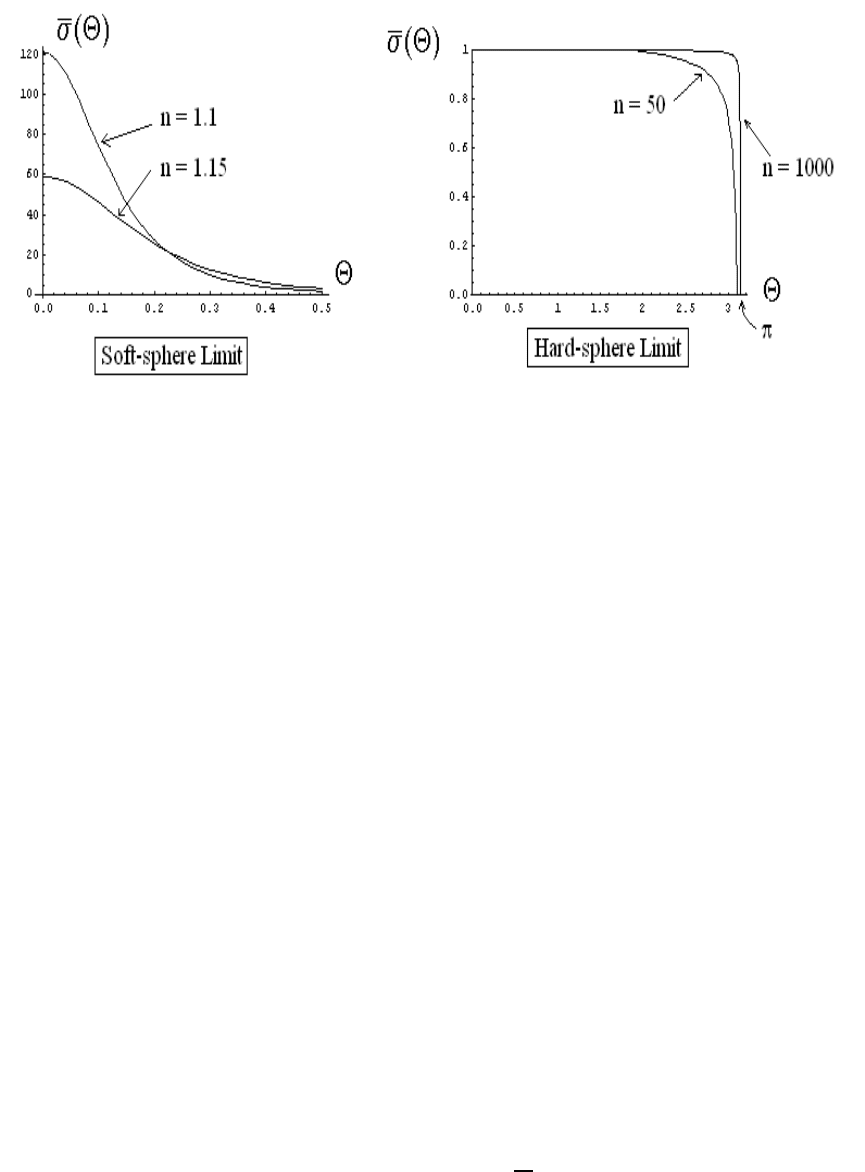
5.7. PROBLEMS 99

Figure 5.8: Soft-sphere scattering cross-section

5.7 Problems

Problem 1

(a) Using the conservation laws of energy and momentum, solve for v

(u, θ; β), where

β = m

and

= u

= v

(cos θ

x + sin θ

= v

(cos ϕ

x − sin ϕ

(b) Discuss the number of physical solutions for v

(u, θ; β) for β<1 and β>1.

(u, θ; β) exist for θ<arcsin(β)=θ

max

Problem 2

Show that the momentum transfer ∆p

= q

− p

of the projectile particle in the CM

frame has a magnitude

|∆p

| =2µu sin

where µ, u, and Θ are the reduced mass, initial projectile LAB speed, and CM scattering

100 CHAPTER 5. COLLISIONS AND SCATTERING THEORY

angle, respectively.

Problem 3

Show that the diﬀerential cross section σ

(Θ) for the elastic scattering of a particle of

mass m from the repulsive central-force potential U(r)=k/r

with a ﬁxed force-center at

r = 0 (or an inﬁnitely massive target particle) is

(Θ) =

2π

(π − Θ)

[Θ (2π − Θ)]

sin Θ

where u is the sp eed of the incoming projectile particle at r = ∞.

Hint : Show that b(Θ) =

(π − Θ)

√

2π Θ − Θ

, where r

2 k

Problem 4

By using the relations tan θ = sin Θ/(α + cos Θ) and/or sin(Θ − θ)=α sin θ, where

α = m

, show that the relation between the diﬀerential cross section in the CM frame,

(Θ), and the diﬀerential cross section in the LAB frame, σ(θ), is

(Θ) = σ( θ) ·

1+α cos Θ

(1 + 2 α cos Θ + α

)

3/2

Problem 5

Consider the scattering of a particle of mass m by the localized attractive central po-

tential

U(r)=











−kr

/2 r ≤ R

0 r>R

where the radius R denotes the range of the interaction.

(a) Show that for a particle of energy E>0 moving towards the center of attraction with

impact parameter b = R sin β, the distance of closest approach ρ for this problem is

ρ =

(e − 1), where e =

2 kb

5.7. PROBLEMS 101

(b) Show that the angle χ at closest approach is

χ = β +

(b/r

) dr

1 − b

+ kr

/2E

= β +

arccos

2 sin

β − 1

(π + Θ) between χ and the CM scattering angle Θ, show that

e =

cos 2β

cos(2β − Θ)

< 1

102 CHAPTER 5. COLLISIONS AND SCATTERING THEORY

Chapter 6

Motion in a Non-Inertial Frame

A reference frame is said to be an inertial frame if the motion of particles in that frame is

subject only to physical forces (i.e., forces are derivable from a physical potential U such

that m

x = −∇U). The Principle of Galilean Relativity states that the laws of physics are

the same in all inertial frames and that all reference frames moving at constant velocity

with resp ect to an inertial frame are also inertial frames. Hence, physical accelerations are

identical in all inertial frames.

In contrast, a reference frame is said to be a non-inertial frame if the motion of particles

in that frame of reference violates the Principle of Galilean Relativity. Such non-inertial

frames include all rotating frames and accelerated reference frames.

6.1 Time Derivatives in Fixed and Rotating Frames

To investigate the relationship between inertial and non-inertial frames, we consider the

time derivative of an arbitrary vector A in two reference frames. The ﬁrst reference frame

is called the ﬁxed (inertial) frame and is expressed in terms of the Cartesian coordinates

=(x

). The second reference frame is called the rotating (non-inertial) frame and

is expressed in terms of the Cartesian coordinates r =(x, y, z). In Figure 6.1, the rotating

frame shares the same origin as the ﬁxed frame and the rotation angular velocity ω of the

rotating frame (with respect to the ﬁxed frame) has components (ω

,ω

Since observations can also be made in a rotating frame of reference, we decomp ose the

vector A in terms of components A

in the rotating frame (with unit vectors

). Thus,

A = A

(using the summation rule) and the time derivative of A as observed in the ﬁxed

frame is

+ A

. (6.1)

The interpretation of the ﬁrst term is that of the time derivative of A as observed in the

103

104 CHAPTER 6. MOTION IN A NON-INERTIAL FRAME

Figure 6.1: Rotating and ﬁxed frames

rotating frame (where the unit vectors

are constant) while the second term involves the

time-dependence of the relation between the ﬁxed and rotating frames. We now express

/dt as a vector in the rotating frame as

= R

= 

ijk

, (6.2)

where R represents the rotation matrix associated with the rotating frame of reference;

this rotation matrix is anti-symmetric (R

= −R

) and can be written in terms of the

anti-symmetric tensor 

ijk

(deﬁned in terms of the vector product A × B = A



ijk

for

two arbitrary vectors A and B)asR

= 

ijk

, where ω

denotes the components of the

angular velocity ω in the rotating frame. Hence, the second term in Eq. (6.1) becomes

= A



ijk

= ω × A. (6.3)

The time derivative of an arbitrary rotating-frame vector A in a ﬁxed frame is, therefore,

expressed as

+ ω × A, (6.4)

where (d/dt)

denotes the time derivative as observed in the ﬁxed (f) frame while (d/dt)

denotes the time derivative as observed in the rotating (r) frame. An important application

of this formula relates to the time derivative of the rotation angular velocity ω itself. One

can easily see that

dω

ω =

dω