Brizard A. An Introduction to Lagrangian Mechanics
Подождите немного. Документ загружается.

6.4. MOTION RELATIVE TO EARTH 115
pendulum motion progressively moves from the East-West axis to the North-South axis.
We now define the complex-valued function
q = y + ix = ` sin θe
iϕ
, (6.39)
so that Eq. (6.38) becomes
¨q + ω
2
0
q − 2iωsin λ ˙q =0.
Next, we now insert the eigenfunction q(t)=ρ exp(iΩt) into this equation and find that
the solution for the eigenfrequency Ω is
Ω=ω sin λ ±
q
ω
2
sin
2
λ + ω
2
0
,
so that the eigenfunction is
q = ρe
iω sin λt
sin
q
ω
2
sin
2
λ + ω
2
0
t
.
By comparing this solution with Eq. (6.39), we finally find
ρ sin
q
ω
2
sin
2
λ + ω
2
0
t
= ` sin θ ' `θ(t),
and
ϕ(t)=(ω sin λ) t,
from which we recover the Foucault pendulum precession frequency (6.37).

116 CHAPTER 6. MOTION IN A NON-INERTIAL FRAME
6.5 Problems
Problem 1
(a) Consider the case involving motion on the (x, y)-plane perpendicular to the angular
velocity vector ω = ω
b
z with the potential energy
U(r)=
1
2
k
x
2
+ y
2
.
Using the Euler-Lagrange equations (6.13), derive the equations of motion for x and y.
(b) By using the equations of motion derived in Part (a), show that the canonical angular
momentum ` =
b
z · (r × p) is a constant of the motion.
Problem 2
If a particle is projected vertically upward to a height h above a point on the Earth’s
surface at a northern latitude λ, show that it strikes the ground at a point
4ω
3
cos λ
s
8 h
3
g
to the west. (Neglect air resistance, and consider only small vertical heights.)
Chapter 7
Rigid Body Motion
7.1 Inertia Tensor
7.1.1 Discrete Particle Distribution
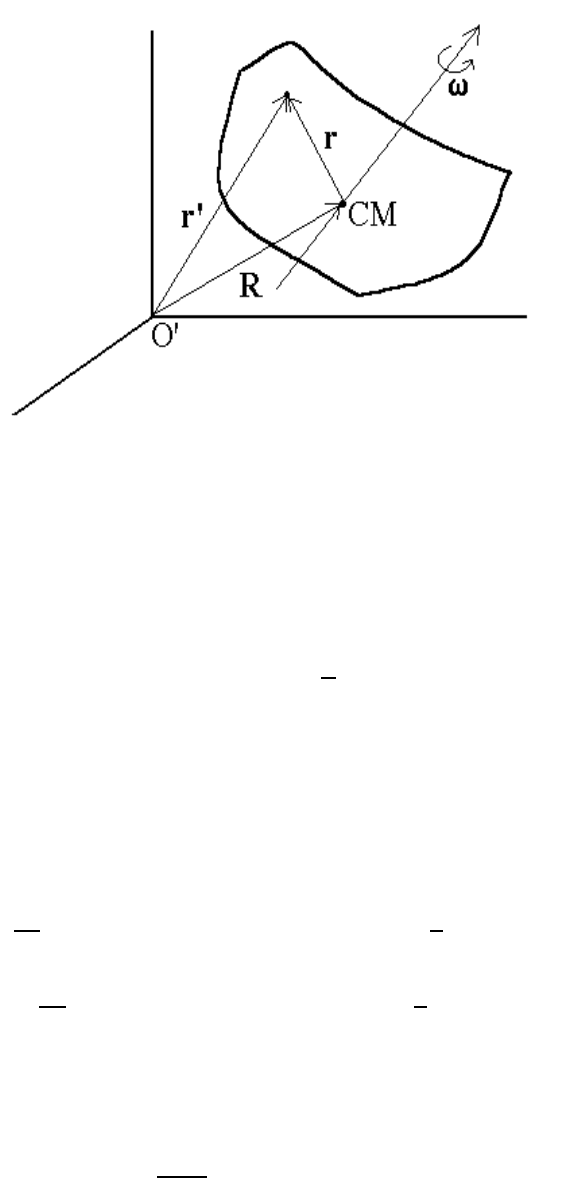
We begin our description of rigid body motion by considering the case of a rigid discrete
particle distribution in which the inter-particle distances are constant. The position of each
particle α as measured from a fixed laboratory (LAB) frame is
r
0
α
= R + r
α
,
where R is the position of the center of mass (CM) in the LAB and r
α
is the position of
the particle in the CM frame. The velocity of particle α in the LAB frame is
v
0
α
= V + ω × r
α
, (7.1)
where ω is the angular velocity vector associated with the rotation of the particle distribu-
tion about an axis of rotation which passes through the CM and V is the CM velocity in
the LAB frame. The total linear momentum in the LAB frame is equal to the momentum
of the center of mass since
P
0
=
X
α
m
α
v
0
α
= M V + ω ×
X
α
m
α
r
α
!
= M V,
where we have used the definition of the total mass of the particle distribution
M =
X
α
m
α
and
X
α
m
α
r
α
=0. (7.2)
Hence, the total momentum of a rigid body in its CM frame is zero. The total angular
momentum in the LAB frame, however, is expressed as
L
0
=
X
α
m
α
r
0
α
× v
0
α
= M R × V +
X
α
m
α
r
α
× ( ω × r
α
) , (7.3)
117

118 CHAPTER 7. RIGID BODY MOTION
Figure 7.1: Discrete distribution of mass
where we have used the identities (7.2).
The kinetic energy of particle α (with mass m
α
) in the LAB frame is
K
0
α
=
m
α
2
|v
0
α
|
2
=
m
α
2
|V|
2
+2V · ω × r
α
+ |ω × r
α
|
2
,
and thus, using the identities (7.2), the total kinetic energy K
0
=
P
α
K
0
α
of the particle
distribution is
K
0
=
M
2
|V|
2
+
1
2
(
ω
2
X
α
m
α
r
2
α
!
− ωω :
X
α
m
α
r
α
r
α
!)
. (7.4)
Looking at Eqs. (7.3) and (7.4), we now introduce the inertia tensor of the particle
distribution
I =
X
α
m
α
r
2
α
1 − r
α
r
α
, (7.5)
where 1 denotes the unit tensor (i.e., in Cartesian coordinates, 1 =
b
x
b
x +
b
y
b
y +
b
z
b
z). The
inertia tensor can also be represented as a matrix
I =
P
α
m
α
(y
2
α
+ z
2
α
) −
P
α
m
α
(x
α
y
α
) −
P
α
m
α
(x
α
z
α
)
−
P
α
m
α
(y
α
x
α
)
P
α
m
α
(x
2
α
+ z
2
α
) −
P
α
m
α
(y
α
z
α
)
−
P
α
m
α
(z
α
x
α
) −
P
α
m
α
(z
α
y
α
)
P
α
m
α
(x
2
α
+ y
2
α
)
, (7.6)
where the symmetry property of the inertia tensor (I
ji
= I
ij
) is readily apparent. In terms
of the inertia tensor (7.5), the angular momentum of a rigid body in the CM frame and its

7.1. INERTIA TENSOR 119
Figure 7.2: Parallel-axes theorem
rotational kinetic energy are
L = I · ω and K
rot
=
1
2
ω · I · ω. (7.7)
7.1.2 Parallel-Axes Theorem
A translation of the origin from which the inertia tensor is calculated leads to a different
inertia tensor. Let Q
α
denote the position of particle α in a new frame of reference (with
its origin located at point P in Figure 7.2) and let ρ = r
α
− Q
α
is the displacement from
point CM to point P . The new inertia tensor
J =
X
α
m
α
Q
2
α
1 − Q
α
Q
α
can be expressed as
J =
X
α
m
α
ρ
2
1 − ρρ
+
X
α
m
α
r
2
α
1 − r
α
r
α
−
(
ρ ·
X
α
m
α
r
α
!)
1 +
(
ρ
X
α
m
α
r
α
!
+
X
α
m
α
r
α
!
ρ
)
.
Since M =
P
α
m
α
and
P
α
m
α
r
α
= 0, we find
J = M
ρ
2
1 − ρρ
+ I
CM
. (7.8)
Hence, once the inertia tensor I
CM
is calculated in the CM frame, it can be calculated
anywhere else. Eq. (7.8) is known as the Parallel-Axes Theorem.
120 CHAPTER 7. RIGID BODY MOTION
Figure 7.3: Continuous distribution of mass
7.1.3 Continuous Particle Distribution
For a continuous particle distribution the inertia tensor (7.5) becomes
I =
Z
dm
r
2
1 − rr
, (7.9)
where dm(r)=ρ(r) d
3
r is the infinitesimal mass element at point r, with mass density
ρ(r).
Consider, for example, the case of a uniform cube of mass M and volume b
3
, with
dm =(M/b
3
) dx dy dz. The inertia tensor (7.9) in the LAB frame (with the origin placed
at one of its corners) has the components
J
11
=
M
b
3
Z
b
0
dx
Z
b
0
dy
Z
b
0
dz ·
y
2
+ z
2
=
2
3
Mb
2
= J
22
= J
33
(7.10)
J
12
= −
M
b
3
Z
b
0
dx
Z
b
0
dy
Z
b
0
dz · xy = −
1
4
Mb
2
= J
23
= J
31
(7.11)
and thus the inertia matrix for the cube is
J =
Mb
2
12
8 −3 −3
−38−3
−3 −38
. (7.12)

7.1. INERTIA TENSOR 121
Figure 7.4: Cube
On the other hand, the inertia tensor calculated in the CM frame has the components
I
11
=
M
b
3
Z
b/2
− b/2
dx
Z
b/2
− b/2
dy
Z
b/2
− b/2
dz ·
y
2
+ z
2
=
1
6
Mb
2
= I
22
= I
33
(7.13)
I
12
= −
M
b
3
Z
b/2
− b/2
dx
Z
b/2
− b/2
dy
Z
b/2
− b/2
dz · xy =0=I
23
= I
31
(7.14)
and thus the CM inertia matrix for the cube is
I =
Mb
2
6
100
010
001
. (7.15)
The displacement vector ρ from the CM point to the corner O is given as
ρ = −
b
2
(
b
x +
b
y +
b
z) ,
so that ρ
2
=3b
2
/4. By using the Parallel-Axis Theorem (7.8), the inertia tensor
M
ρ
2
1 − ρρ
=
Mb
2
4
2 −1 −1
−12−1
−1 −12
when added to the CM inertia tensor (7.15), yields the inertia tensor (7.12)

122 CHAPTER 7. RIGID BODY MOTION
7.1.4 Principal Axes of Inertia
In general, the CM inertia tensor I can be made into a diagonal tensor with components
given by the eigenvalues I
1
, I
2
, and I
3
of the inertia tensor. These comp onents (known as
principal moments of inertia) are the three roots of the cubic polynomial
I
3
− Tr(I) I
2
+ Ad(I) I − Det(I)=0, (7.16)
obtained from Det(I − I 1
) = 0, with coefficients
Tr(I)=I
11
+ I
22
+ I
33
,
Ad(I)=ad
11
+ad
22
+ad
33
,
Det(I)=I
11
ad
11
− I
12
ad
12
+ I
13
ad
13
,
where ad
ij
is the determinant of the two-by-two matrix obtained from I by removing the
i
th
-row and j
th
-column from the inertia matrix I.
Each principal moment of inertia I
i
represents the moment of inertia calculated about
the principal axis of inertia with unit vector
b
e
i
. The unit vectors (
b
e
1
,
b
e
2
,
b
e
3
) form a new
frame of reference known as the Body frame. The unit vectors (
b
e
1
,
b
e
2
,
b
e
3
) are related by a
sequence of rotations to the Cartesian CM unit vectors (
b
x
1
,
b
x
2
,
b
x
3
) by the relation
b
e
i
= R
ij
b
x
j
, (7.17)
where R
ij
are components of the rotation matrix R. By denoting as I
0
the diagonal inertia
tensor calculated in the body frame of reference (along the principal axes), we find
I
0
= R · I · R
T
=
I
1
00
0 I
2
0
00I
3
, (7.18)
where R
T
denotes the transpose of R, i.e., ( R
T
)
ij
= R
ji
. In the body frame, the inertia
tensor is, therefore, expressed in dyadic form as
I
0
= I
1
b
e
1
b
e
1
+ I
2
b
e
2
b
e
2
+ I
3
b
e
3
b
e
3
, (7.19)
and the rotational kinetic energy (7.7) is
K
0
rot
=
1
2
ω · I
0
· ω =
1
2
I
1
ω
2
1
+ I
2
ω
2
2
+ I
3
ω
2
3
. (7.20)
Note that general rotation matrices have the form
R
n
(α)=
b
n
b
n + cos α (1 −
b
n
b
n) − sin α
b
n × 1, (7.21)
7.1. INERTIA TENSOR 123
Figure 7.5: Dumbbell
where the unit vector
b
n defines the axis of rotation about which an angular rotation of
angle α is p erformed according to the right-hand-rule.
A rigid b ody can be classified according to three categories. First, a rigid bo dy is said
to be a spherical top if its three principal moments of inertia are equal (I
1
= I
2
= I
3
),
i.e., the three roots of the cubic polynomial (7.16) are triply degenerate. Next, a rigid
body is said to b e a symmetric top if two of its principal moments of inertia are equal
(I
1
= I
2
6= I
3
), i.e., I
3
is a single root and I
1
= I
2
are doubly-degenerate roots of the cubic
polynomial (7.16). Lastly, when the three roots (I
1
6= I
2
6= I
3
) are all single roots of the
cubic polynomial (7.16), a rigid b ody is said to be an asymmetric top.
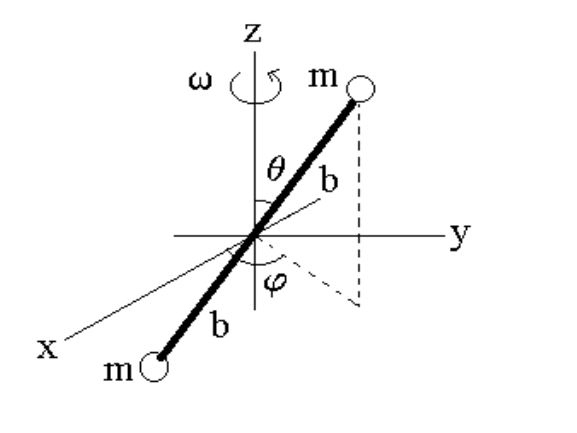
Before proceeding further, we consider the example of a dumbbell composed of two
equal point masses m placed at the ends of a massless rod of total length 2 b and rotating
about the z-axis with angular frequency ω. Here, the positions of the two masses are
expressed as
r
±
= ±b [sin θ (cos ϕ
b
x + sin ϕ
b
y) + cos θ
b
z ] ,
so that the CM inertia tensor is
I =2mb
2
1 −cos
2
ϕ sin
2
θ − cos ϕ sin ϕ sin
2
θ − cos ϕ cos θ sin θ
− cos ϕ sin ϕ sin
2
θ 1 −sin
2
ϕ sin
2
θ − sin ϕ cos θ sin θ
− cos ϕ cos θ sin θ − sin ϕ cos θ sin θ 1 −cos
2
θ
. (7.22)
After some tedious algebra, we find Tr(I)=4mb
2
, Ad(I)=(2mb
2
)
2
, and Det(I)=0,
and thus the cubic polynomial (7.16) has the single root I
3
= 0 and the double root
I
1
= I
2
=2mb
2
, which makes the dumbbell a symmetric top.

124 CHAPTER 7. RIGID BODY MOTION
The root I
3
= 0 clearly indicates that one of the three principal axes is the axis of
symmetry of the dumbbell (
b
e
3
=
b
r). The other two principal axes are lo cated on the
plane perp endicular to the symmetry axis (i.e.,
b
e
1
=
b
θ and
b
e
2
=
b
ϕ). From these choices,
we easily recover the rotation matrix
R = R
2
(−θ) · R
3
(ϕ)=
cos ϕ cos θ sin ϕ cos θ − sin θ
− sin ϕ cos ϕ 0
cos ϕ sin θ sin ϕ sin θ cos θ
,
so that, using the spherical coordinates (r, θ, ϕ), we find
b
e
1
= cos θ (cos ϕ
b
x + sin ϕ
b
y) − sin θ
b
z =
b
θ,
b
e
2
= − sin ϕ
b
x + cos ϕ
b
y =
b
ϕ,
b
e
3
= sin θ (cos ϕ
b
x + sin ϕ
b
y)+cosθ
b
z =
b
r.
Indeed, the principal moment of inertia about the
b
r-axis is zero, while the principal moments
of inertia ab out the perpendicular
b
θ- and
b
ϕ-axes are equally given as 2 mb
2
.
7.2 Angular Momentum
7.2.1 Euler Equations
The time derivative of the angular momentum L = I · ω in the fixed (LAB) frame is given
as
dL
dt
!
f
=
dL
dt
!
r
+ ω × L = N,
where N represents the external torque applied to the system and (dL/dt)
r
denotes the
rate of change of L in the rotating frame. By choosing the body frame as the rotating
frame, we find
dL
dt
!
r
= I ·
˙
ω =(I
1
˙ω
1
)
b
e
1
+(I
2
˙ω
2
)
b
e
2
+(I
3
˙ω
3
)
b
e
3
, (7.23)
while
ω × L = −
b
e
1
{ ω
2
ω
3
(I
2
− I
3
) }−
b
e
2
{ ω
3
ω
1
(I
3
− I
1
) }−
b
e
3
{ ω
1
ω
2
(I
1
− I
2
) }.
(7.24)
Thus the time evolution of the angular momentum in the body frame of reference is de-
scrib ed in terms of
I
1
˙ω
1
− ω
2
ω
3
(I
2
− I
3
)=N
1
I
2
˙ω
2
− ω
3
ω
1
(I
3
− I
1
)=N
2
I
3
˙ω
3
− ω
1
ω
2
(I
1
− I
2
)=N
3
, (7.25)
