Brizard A. An Introduction to Lagrangian Mechanics

Подождите немного. Документ загружается.

7.3. SYMMETRIC TOP WITH ONE FIXED POINT 135

Figure 7.11: Orbits of heavy top – Case II

Figure 7.12: Orbits of heavy top – Case III

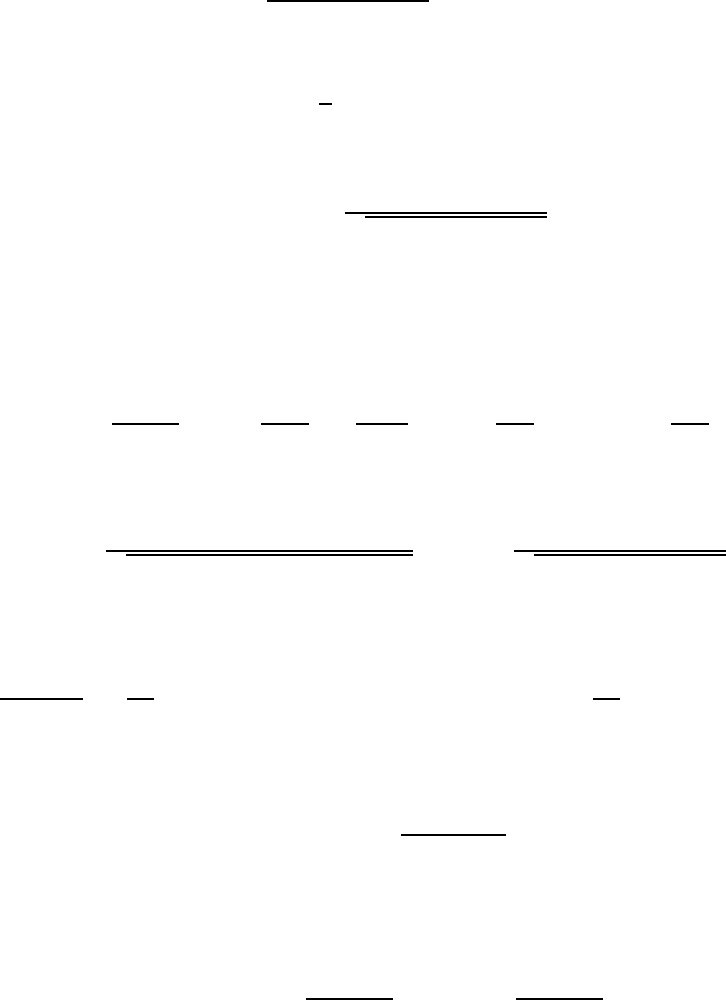
136 CHAPTER 7. RIGID BODY MOTION

and an eﬀective potential energy

V (θ)=

−p

cos θ)

sin

+ Mgh cos θ, (7.54)

so that Eq. (7.53) becomes

(t)+V (θ), (7.55)

which can be formally solved as

t(θ)=±

dθ

(2/I

)[E

− V (θ)]

. (7.56)

Note that turning points θ

are again deﬁned as roots of the equation E

= V (θ).

A simpler formulation for this problem is obtained as follows. First, we deﬁne the

following quantities

Ω

2 Mgh

,=

2 E

Ω

Mgh

,α=

Ω

, and β =

Ω

, (7.57)

so that Eq. (7.56) becomes

τ(u)=±

(1 − u

)( − u) − (α − βu)

= ±

(1 − u

)[ − W (u)]

, (7.58)

where τ (u)=Ωt(u), u = cos θ, and the energy equation (7.55) becomes

 =

(1 − u

)





dτ

+(α − βu)





+ u =(1− u

)

−1

dτ

+ W (u), (7.59)

where the eﬀective potential is

W (u)=u +

(α − βu)

(1 − u

)

We note that the eﬀective potential W (u) is inﬁnite at u = ±1 and has a single minimum

at u = u

(or θ = θ

) deﬁned by the quartic equation

)=1+2u

α −βu

1 − u

− 2β

α −βu

1 −u

=0. (7.60)

This equation has four roots: two roots are complex roots, a third root is always greater

than one for α>0 and β>0 (which is unphysical since u = cos θ ≤ 1), while the fourth

root is less than one for α>0 and β>0; hence, this root is the only physical root

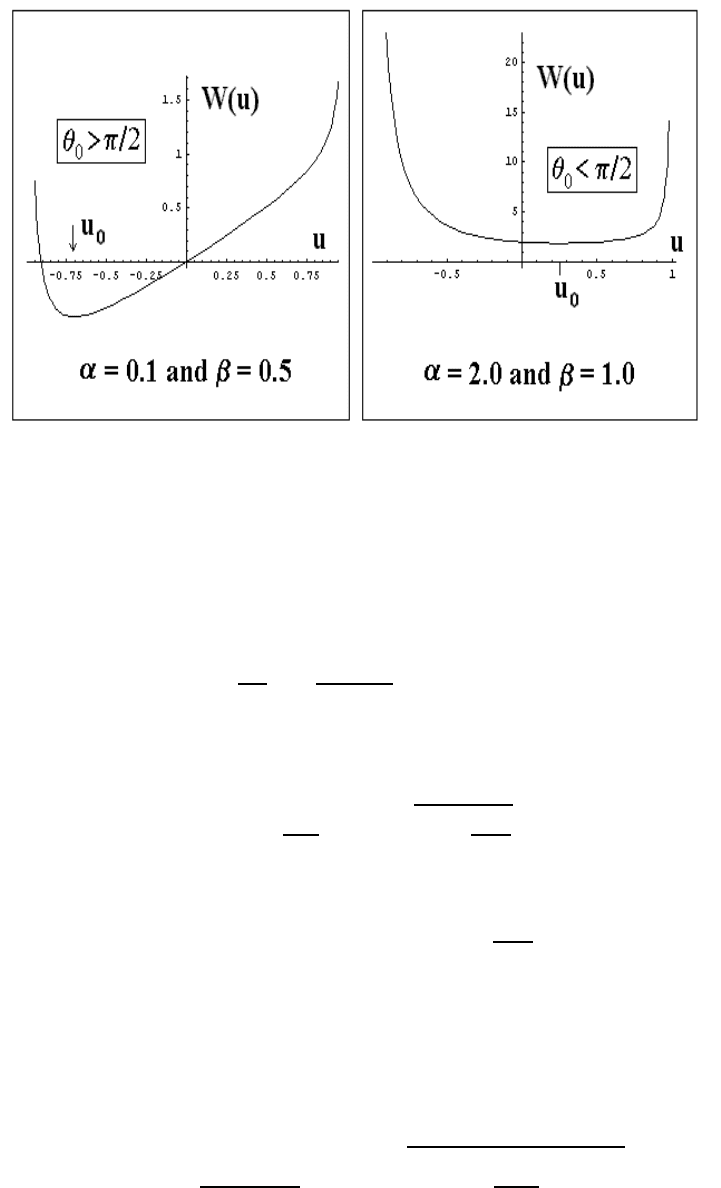
corresponding to a single minimum for the eﬀective potential W (u) (see Figure 7.13). Note

7.3. SYMMETRIC TOP WITH ONE FIXED POINT 137

Figure 7.13: Eﬀective p otential for the heavy top

how the linear gravitational-potential term u is apparent at low values of α and β.

We ﬁrst investigate the motion of the symmetric top at the minimum angle θ

for which

 = W (u

) and ˙u(u

) = 0. For this purpose, we note that when the dimensionless azimuthal

frequency

dϕ

dτ

α − βu

1 − u

= ν(u)

is inserted in Eq. (7.60), we obtain the quadratic equation 1 + 2u

− 2βν

= 0, which

has two solutions for ν

= ν(u

ν(u

1 ±

1 −

2 u

Here, we further note that these solutions require that the radicand be positive, i.e.,

> 2 u

or I

≥ I

Ω

√

2 u

if u

≥ 0 (or θ

≤ π/2); no conditions are applied to ω

for the case u

< 0 (or θ

>π/2)

since the radicand is strictly positive in this case.

Hence, the precession frequency ˙ϕ

= ν(u

)Ω at θ = θ

has a slow component and a

fast component

(˙ϕ

)

slow

2 I

cos θ







1 −

1 − 2



Ω



cos θ







138 CHAPTER 7. RIGID BODY MOTION

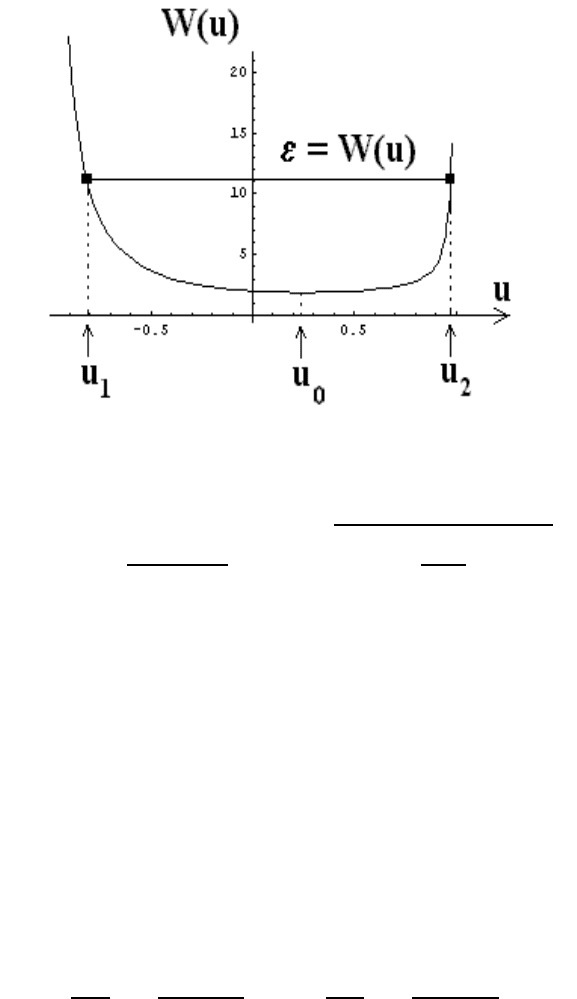
Figure 7.14: Turning-point roots

(˙ϕ

)

fast

2 I

cos θ







1 − 2



Ω



cos θ







We note that for θ

<π/2 (or cos θ

> 0) the two precession frequencies ( ˙ϕ

)

slow

and ( ˙ϕ

)

fast

have the same sign while for θ

>π/2 (or cos θ

< 0) the two precession frequencies have

opposite signs ( ˙ϕ

)

slow

< 0 and ( ˙ϕ

)

fast

> 0.

Next, we investigate the case with two turning points u

and u

(or θ

>θ

)

where  = W (u) (see Figure 7.14), where the θ-dynamics oscillates between θ

and θ

. The

turning p oints u

and u

are roots of the function

F (u)=(1− u

)[ − W (u)] = u

− ( + β

) u

− (1 − 2 αβ) u +( − α

). (7.61)

Although a third root u

exists for F(u) = 0, it is unphysical since u

> 1.

Since the azimuthal frequencies at the turning p oints are expressed as

dϕ

dτ

α − βu

1 − u

and

dϕ

dτ

α −βu

1 − u

where α−βu

>α− βu

, we can study the three cases for nutation numerically investigated

below Eqs. (7.52); here, we assume that both α = bβ and β are positive. In Case I

(α>βu

), the precession frequency dϕ/dτ is strictly positive for u

≤ u ≤ u

and

nutation pro ceeds monotonically. In Case II ( α = βu

), the precession frequency dϕ/dτ is

positive for u

≤ u<u

and vanishes at u = u

; nutation in this Case exhibits a cusp at θ

In Case II I (α<βu

), the precession frequency dϕ/dτ reverses its sign at u

= α/β = b

or θ

<θ

= arccos(b) <θ

7.3. SYMMETRIC TOP WITH ONE FIXED POINT 139

7.3.5 Stability of the Sleeping Top

Let us consider the case where a symmetric top with one ﬁxed point is launched with

initial conditions θ

6= 0 and

=˙ϕ

= 0, with

6= 0. In this case, the invariant canonical

momenta are

= I

and p

= p

cos θ

These initial conditions (u

= α/β, ˙u

= 0), therefore, imply from Eq. (7.59) that  = u

and that the energy equation (7.59) now becomes

dτ

(1 − u

) − β

− u)

− u). (7.62)

Next, we consider the case of the sleeping top for which an additional initial condition

is θ

= 0 (and u

= 1). Thus Eq. (7.62) becomes

dτ



1+u − β



(1 −u)

. (7.63)

The sleeping top has the following equilibrium points (where ˙u = 0): u

= 1 and u

= β

−1.

We now investigate the stability of the equilibrium p oint u

= 1 by writing u =1−δ (with

δ  1) so that Eq. (7.63) becomes

dδ

dτ



2 −β



δ.

The solution of this equation is exponential (and, therefore, u

is unstable) if β

< 2

or oscillatory (and, therefore, u

is stable) if β

> 2. Note that in the latter case, the

condition β

> 2 implies that the second equilibrium point u

= β

− 1 > 1 is unphysical.

We, therefore, see that stability of the sleeping top requires a large spinning frequency ω

;

in the presence of friction, the spinning frequency slows down and ultimately the sleeping

top becomes unstable.

140 CHAPTER 7. RIGID BODY MOTION

7.4 Problems

Problem 1

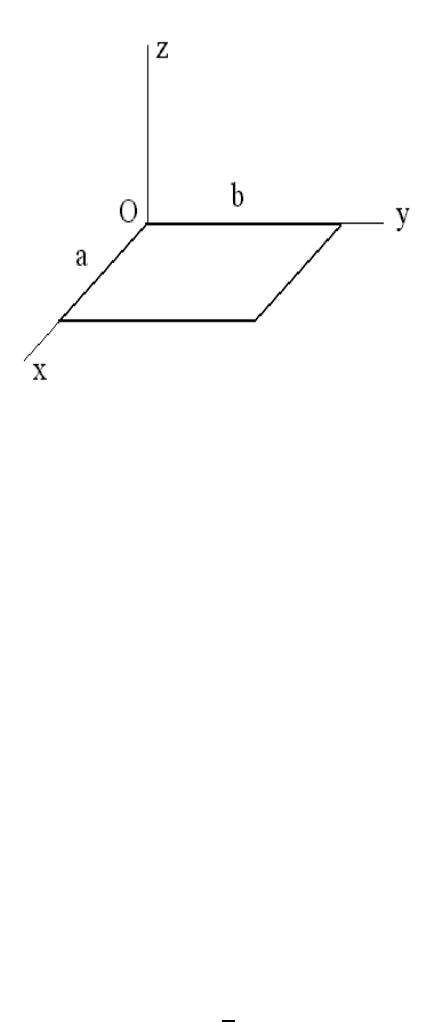
Consider a thin homogeneous rectangular plate of mass M and area ab that lies on the

(x, y)-plane.

(a) Show that the inertia tensor (calculated in the reference frame with its origin at point

O in the Figure ab ove) takes the form

I =







A −C 0

−CB 0

00A + B







and ﬁnd suitable expressions for A, B, and C in terms of M, a, and b.

(b) Show that by p erforming a rotation of the coordinate axes about the z-axis through an

angle θ, the new inertia tensor is

(θ)=R(θ) · I · R

(θ)=







−C

00A

+ B







where

= A cos

θ + B sin

θ − C sin 2θ

= A sin

θ + B cos

θ + C sin 2θ

= C cos 2θ −

(B − A) sin 2θ.

7.4. PROBLEMS 141

θ =

arctan



B − A



the oﬀ-diagonal component C

vanishes and the x

− and y

−axes become principal axes.

Calculate expressions for A

and B

in terms of M, a, and b for this particular angle.

(d) Calculate the inertia tensor I

in the CM frame by using the Parallel-Axis Theorem

and show that

, and I



+ a



Problem 2

(a) The Euler equation for an asymmetric top (I

) with L

=2I

K is

˙ω

= α



Ω

− ω



where

Ω

and α =



1 −



− 1



Solve for ω

(t) with the initial condition ω

(0) = 0.

(b) Use the solution ω

(t) found in Part (a) to ﬁnd the solutions ω

(t) and ω

(t) given by

Eqs. (7.35).

Problem 3

(a) Consider a circular cone of height H and base radius R = H tan α with uniform mass

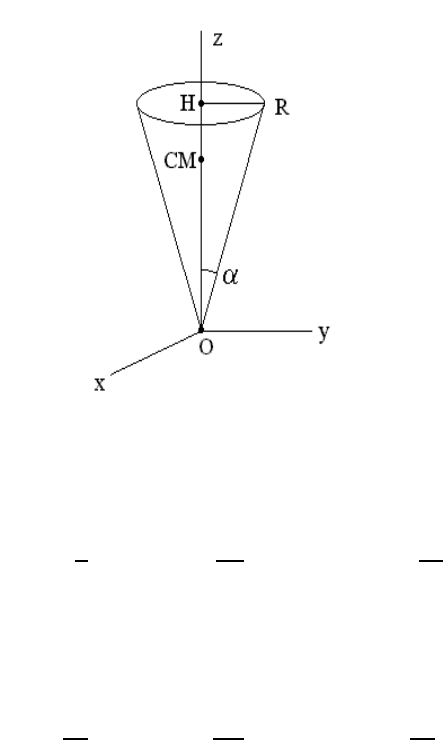
142 CHAPTER 7. RIGID BODY MOTION

density ρ =3M/( πHR

Show that the non-vanishing components of the inertia tensor I calculated from the

vertex O of the cone are

= I

and I

(b) Show that the principal moments of inertia calculated in the CM frame (located at a

height h =3H/4 on the symmetry axis) are

= I

and I

Problem 4

Show that the Euler basis vectors (

) are expressed as shown in Eq. (7.41).

Chapter 8

Normal-Mode Analysis

8.1 Stability of Equilibrium Points

A nonlinear force equation m ¨x = f(x) has equilibrium p oints (labeled x

) when f( x

)

vanishes. The stability of the equilibrium point x

is determined by the sign of f

): the

equilibrium point x

is stable if f

) < 0 or it is unstable if f

) > 0. Since f(x) is also

derived from a potential V (x)asf(x)=−V

(x), we say that the equilibrium point x

stable (or unstable) if V

) is positive (or negative).

8.1.1 Bead on a Rotating Hoop

In Chap. 2, we considered the problem of a bead of mass m sliding freely on a hoop of

radius r rotating with angular velocity ω

in a constant gravitational ﬁeld with acceleration

g. The Lagrangian for this system is

L(θ,

θ)=



sin

θ + mgr cos θ



− V (θ),

where V (θ) denotes the eﬀective potential, and the Euler-Lagrange equation for θ is

θ = −V

(θ)=− mr

sin θ (ν − cos θ), (8.1)

where ν = g/(rω

). The equilibrium points of Eq. (8.1) are θ = 0 (for all values of ν) and

θ = arccos(ν)ifν<1. The stability of the equilibrium point θ = θ

is determined by the

sign of

(θ

)=mr

ν cos θ

−



2 cos

− 1

i

Hence,

(0) = mr

(ν − 1) (8.2)

143

144 CHAPTER 8. NORMAL-MODE ANALYSIS

Figure 8.1: Bifurcation tree for the bead on a rotating-hoop problem

is positive (i.e., θ = 0 is stable) if ν>1 or negative (i.e., θ = 0 is unstable) if ν<1. In

the latter case, when ν<1 and the second equilibrium point θ

= arccos (ν) is p ossible, we

ﬁnd

(θ

)=mr

−



2 ν

− 1

i

= mr



1 −ν



> 0, (8.3)

and thus the equilibrium point θ

= arccos(ν) is stable when ν<1. The stability of the

bead on a rotating hoop is displayed on the bifurcation diagram (see Figure 7.14) which

shows the stable regime bifurcates at ν =1.

8.1.2 Circular Orbits in Central-Force Fields

The radial force equation

µ ¨r =

µr

−

= −V

(r),

studied in Chap. 4 for a central-force ﬁeld F (r)=−kr

−n

(here, µ is the reduced mass

of the system, the azimuthal angular momentum ` is a constant of the motion, and k is a

constant), has the equilibrium point at r = ρ deﬁned by the relation

n−3

µk

. (8.4)

The second derivative of the eﬀective potential is

(r)=

µr

3 − n

kµ

n−3