Brealey, Myers. Principles of Corporate Finance. 7th edition

Подождите немного. Документ загружается.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VI. Options 23. Warrants and

Convertibles

Companies, 2003

CHAPTER 23 Warrants and Convertibles 663

Visit us at www.mhhe.com/bm7e

• Stock: 36 million shares, which closed at $10 per share on the day before the murder. The

company had just announced a regular quarterly dividend of $.10 per share, and the

shares were due to go ex-dividend in two weeks.

• Warrants: Warrants to buy an additional four million shares at $10 per share, expiring in

three months time on December 31, 2003. The recent volatility of the shares had been

around 50 percent per annum.

Yesterday Thorndike had flatly rejected an offer by T. Spoone Dickens to buy all

Thorndike’s assets for $1 billion cash, effective January 1, 2004. With Thorndike out of the

way, it appeared that Dickens’s offer would be accepted, much to the profit of Thorndike

Oil’s other shareholders.

Thorndike’s two nieces, Doris and Patsy, and his nephew John all had substantial in-

vestments in Thorndike Oil and had bitterly disagreed with Thorndike’s dismissal of Dick-

ens’s offer. Their stakes are shown in the table below.

All debt issued by Thorndike Oil would be paid off at face value if Dickens’s offer went

through.

Morse kept coming back to the problem of motive. Which niece or nephew, he wondered,

stood to gain most by eliminating Thorndike and allowing Dickens’s offer to succeed?

Rupert Thorndike’s shares would go to a charitable foundation formed to “advance the study of fi-

nancial engineering and its crucial role in world peace and progress.” The managers of the foundation’s

endowment were not expected to oppose the takeover.

Debt Stock Warrants

(Face Value) (Number of Shares, in Millions) (Number, in Millions)

Doris $6 million 1.0 0

John 0 .5 2

Patsy 0 1.5 1

Questions

Help Morse by answering the following questions:

1. Value the company’s debt, stock, and warrants both before and after Mr. Thorndike’s

death.

2. Which of Thorndike’s relatives stood to gain most from his death?

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VI. Options 23. Warrants and

Convertibles

Companies, 2003

RELATED WEBSITES

The Chicago Board site contains explanations of

options markets and lots of data:

www

.cboe.com

There are a number of good options sites, many

of which provide data and calculators for

Black–Scholes values and implied standard

deviations:

www

.cfo.com

www

.fintools.net/options/optcalc.html

(very good calculators)

www

.numa.com

www.optionscentral.com

www.pcquote.com/options

www.pmpublishing.com (includes historical

implied volatilities)

www.schaffersresearch.com/stock/

calculator

.asp

Two sites devoted to real options are:

www

.real-options.com

www

.puc-rio.br/marco.ind

Examples of journals specializing in options

and other derivatives include:

www

.appliederivatives.com

www

.erivativesreview.com

www.futuresmag.com

www.risk.com

PART SIX

WEBSITES

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

CHAPTER TWENTY-FOUR

666

VALUING DEBT

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

HOW DO YOU estimate the present value of a company’s bonds? The answer is simple: You take the cash

flows and discount them at the opportunity cost of capital. Therefore, if a bond produces cash flows of

C dollars per year for N years and is then repaid at its face value ($1,000), the present value is

where are the appropriate discount rates for the cash flows to be received by the bond

owners in periods

That is correct as far as it goes but it does not tell us anything about what determines the discount

rates. For example,

• In 1945 U.S. Treasury bills offered a return of .4 percent: At their 1981 peak they offered a re-

turn of over 17 percent. Why does the same security offer radically different yields at different

times?

• In mid-2001 the U.S. Treasury could borrow for one year at an interest rate of 3.4 percent, but it

had to pay nearly 6 percent for a 30-year loan. Why do bonds maturing at different dates offer dif-

ferent rates of interest? In other words, why is there a term structure of interest rates?

• In mid-2001 the United States government could issue long-term bonds at a rate of nearly

6 percent. But even the most blue-chip corporate issuers had to pay at least 50 basis points

(.5 percent) more on their long-term borrowing. What explains the premium that firms have

to pay?

These questions lead to deep issues that will keep economists simmering for years. But we can give

general answers and at the same time present some fundamental ideas.

Why should the financial manager care about these ideas? Who needs to know how bonds are

priced as long as the bond market is active and efficient? Efficient markets protect the ignorant

trader. If it is necessary to know whether the price is right for a proposed bond issue, you can check

the prices of similar bonds. There is no need to worry about the historical behavior of interest rates,

about the term structure, or about the other issues discussed in this chapter.

We do not believe that ignorance is desirable even when it is harmless. At least you ought to be

able to read the bond tables in The Wall Street Journal and talk to investment bankers about the

prices of recently issued bonds. More important, you will encounter many problems of bond pricing

where there are no similar instruments already traded. How do you evaluate a private placement with

a custom-tailored repayment schedule? How about financial leases? In Chapter 26 we will see that

they are essentially debt contracts, but often extremely complicated ones, for which traded bonds

are not close substitutes. Many companies, notably banks and insurance firms, are exposed to the

risk of interest rate fluctuations. To control their exposure, these companies need to understand how

interest rates change.

You will find that the terms, concepts, and facts presented in this chapter are

essential to the analysis of these and other practical problems.

We start the chapter with our first question: Why does the general level of interest rates change

over time? Next we turn to the relationship between short- and long-term interest rates. We consider

three issues:

• Each period’s cash flow on a bond potentially needs to be discounted at a different interest rate,

but bond investors often calculate the yield to maturity as a summary measure of the interest rate

on the bond. We first explain how these measures are related.

continued

1, 2, . . . , N.

, r

, . . . , r

PV ⫽

1 ⫹ r

⫹

11 ⫹ r

⫹

…

⫹

11 ⫹ r

⫹

$1,000

11 ⫹ r

667

We discuss in Chapter 27 how firms protect themselves against interest rate risk.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

Indexed Bonds and the Real Rate of Interest

In Chapter 3 we drew the distinction between the real and nominal rate of interest.

Most bonds promise a fixed nominal rate of interest. The real interest rate that you

receive depends on the inflation rate. For example, if a one-year bond promises you

a return of 10 percent and the expected inflation rate is 4 percent, the expected real

return on your bond is , or 5.8 percent. Since future inflation

rates are uncertain, the real return on a bond is also uncertain. For example, if in-

flation turns out to be higher than the expected 4 percent, the real return will be

lower than 5.8 percent.

You can nail down a real return; you do so by buying an indexed bond whose

payments are linked to inflation. Indexed bonds have been around in many coun-

tries for decades, but they were almost unknown in the United States until 1997

when the U.S. Treasury began to issue inflation-indexed bonds known as TIPs

(Treasury Inflation-Protected Securities).

The real cash flows on TIPs are fixed, but the nominal cash flows (interest and

principal) are increased as the Consumer Price Index increases. For example, sup-

pose that the U.S. Treasury issues 3 percent 20-year TIPs at a price of 100. If during

the first year the Consumer Price Index rises by (say) 10 percent, then the coupon

payment on the bond would be increased by 10 percent to percent.

And the final payment of principal would also be increased in the same proportion

to percent. Thus, an investor who buys the bond at the issue

price and holds it to maturity can be assured of a real yield of 3 percent.

As we write this in the summer of 2001, long-term TIPs offer a yield of 3.46 per-

cent. This yield is a real yield: It measures how much extra goods your investment

would allow you to buy. The 3.46 percent yield on TIPs was about 2.3 percent less

than on nominal Treasury bonds. If the annual inflation rate proves to be higher

than 2.3 percent, you will earn a higher return by holding long-term TIPs; if the in-

flation rate is lower than 2.3 percent, the reverse will be true.

What determines the real interest rate that investors demand? The classical econ-

omist’s answer to this question is summed up in the title of Irving Fisher’s great

book: The Theory of Interest: As Determined by Impatience to Spend Income and Opportu-

nity to Invest It.

The real interest rate, according to Fisher, is the price which equates

11.1 ⫻ 1002⫽ 110

11.1 ⫻ 32⫽ 3.3

1.10/1.04 ⫺ 1 ⫽ .058

668 PART VII

Debt Financing

• Second, we show why a change in interest rates has a greater impact on the price of long-term

loans than on short-term loans.

• Finally, we look at some theories that explain why short- and long-term interest rates differ.

To close the chapter we shift the focus to corporate bonds and examine the risk of default and its ef-

fect on bond prices.

24.1 REAL AND NOMINAL RATES OF INTEREST

In 1988 Franklin Savings Association had issued a 20-year bond whose interest (but not principal) was

tied to the rate of inflation. Since then a trickle of companies has also issued indexed bonds.

August M. Kelley, New York, 1965; originally published in 1930.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

the supply and demand for capital. The supply depends on people’s willingness to

save.

The demand depends on the opportunities for productive investment.

For example, suppose that investment opportunities generally improve. Firms

have more good projects, so they are willing to invest more than previously at any

interest rate. Therefore, the rate has to rise to induce individuals to save the addi-

tional amount that firms want to invest.

Conversely, if investment opportunities

deteriorate, there will be a fall in the real interest rate.

Fisher’s theory emphasizes that the required real rate of interest depends on real

phenomena. A high aggregate willingness to save may be associated with high ag-

gregate wealth (because wealthy people usually save more), an uneven distribu-

tion of wealth (an even distribution would mean fewer rich people, who do most

of the saving), and a high proportion of middle-aged people (the young don’t need

to save and the old don’t want to—“You can’t take it with you”). Correspondingly,

a high propensity to invest may be associated with a high level of industrial activ-

ity or major technological advances.

Real interest rates do change but they do so gradually. We can see this by look-

ing at the UK, where the government has issued indexed bonds since 1982. The col-

ored line in Figure 24.1 shows that the (real) yield on these bonds has fluctuated

within a relatively narrow range, while the yield on nominal government bonds

has declined dramatically.

Inflation and Nominal Interest Rates

Now let us see what Irving Fisher had to say about inflation and interest rates. Sup-

pose that consumers are equally happy with 100 apples today or 105 apples in a

year’s time. In this case the real or “apple” interest rate is 5 percent. Suppose also

CHAPTER 24

Valuing Debt 669

Some of this saving is done indirectly. For example, if you hold 100 shares of GM stock, and GM re-

tains earnings of $1 per share, GM is saving $100 on your behalf.

We assume that investors save more as interest rates rise. It doesn’t have to be that way; here is an ex-

ample of how a higher interest rate could mean less saving: Suppose that 20 years hence you will need

$50,000 at current prices for your children’s college expenses. How much will you have to set aside to-

day to cover this obligation? The answer is the present value of a real expenditure of $50,000 after 20

years, or . The higher the real interest rate, the lower the present value

and the less you have to set aside.

50,000/1 1 ⫹ real interest rate2

Dec. 83

Dec. 84

Dec. 85

Dec. 86

Dec. 87

Dec. 88

Dec. 89

Dec. 90

Dec. 91

Dec. 92

Dec. 93

Dec. 94

Dec. 95

Dec. 96

Dec. 97

Dec. 98

Dec. 99

Dec. 00

Percent

Real yield on UK indexed bonds

Yield on UK nominal bonds

FIGURE 24.1

The burgundy line shows the real yield

on long-term indexed bonds issued by

the UK government. The blue line

shows the yield on UK government

long-term nominal bonds. Notice that

the real yield has been much more

stable than the nominal yield.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

that I know the price of apples will increase over the year by 10 percent. Then I will

part with $100 today if I am repaid $115 at the end of the year. That $115 is needed

to buy me 5 percent more apples than I can get for my $100 today. In other words,

the nominal, or “money,” rate of interest must equal the required real, or “apple,”

rate plus the prospective rate of inflation.

A change of 1 percent in the expected in-

flation rate produces a change of 1 percent in the nominal interest rate. That is

Fisher’s theory: A change in the expected inflation rate will cause the same change

in the nominal interest rate; it has no effect on the required real interest rate.

Nominal interest rates cannot be negative; if they were, everyone would prefer

to hold cash, which pays zero interest.

But what about real rates? For example, is

it possible for the money rate of interest to be 5 percent and the expected rate of in-

flation to be 10 percent, thus giving a negative real interest rate? If this happens,

you may be able to make money in the following way: You borrow $100 at an in-

terest rate of 5 percent and you use the money to buy apples. You store the apples

and sell them at the end of the year for $110, which leaves you enough to pay off

your loan plus $5 for yourself.

Since easy ways to make money are rare, we can conclude that if it doesn’t cost

anything to store goods, the money rate of interest can’t be less than the expected

rise in prices. But many goods are even more expensive to store than apples, and

others can’t be stored at all (you can’t store haircuts, for example). For these goods,

the money interest rate can be less than the expected price rise.

How Well Does Fisher’s Theory Explain Interest Rates?

Not all economists would agree with Fisher that the real rate of interest is unaf-

fected by the inflation rate. For example, if changes in prices are associated with

changes in the level of industrial activity, then in inflationary conditions I might

want more or less than 105 apples in a year’s time to compensate me for the loss of

100 today.

We wish we could show you the past behavior of interest rates and expected in-

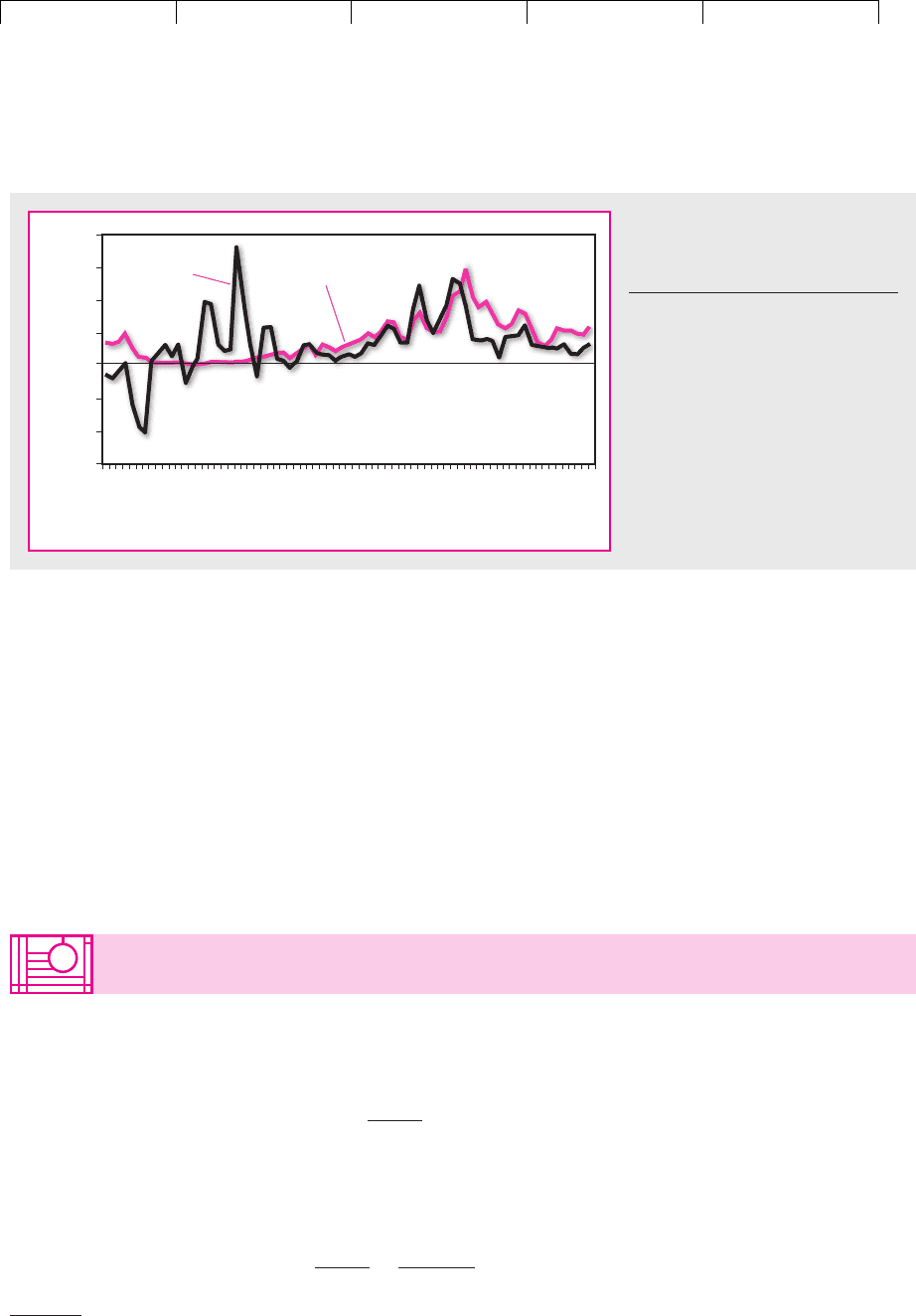
flation. Instead we have done the next best thing and plotted in Figure 24.2 the re-

turn on U.S. Treasury bills against actual inflation. Notice that between 1926 and

1981 the return on Treasury bills was below the inflation rate about as often as it

670 PART VII

Debt Financing

We oversimplify. If apples cost $1.00 apiece today and $1.10 next year, you need

next year to buy 105 apples. The money rate of interest is 15.5 percent, not 15. Remember, the exact for-

mula relating real and money rates is

where i is the expected inflation rate. Thus

In our example, the money rate should be

When we said the money rate should be 15 percent, we ignored the cross-product term i . This is

a common rule of thumb because the cross-product term is usually small. But there are countries where

i is large (sometimes 100 percent or more). In such cases it pays to use the full formula.

The apple example was taken from R. Roll, “Interest Rates on Monetary Assets and Commodity Price

Index Changes,” Journal of Finance 27 (May 1972), pp. 251–278.

There seems to be an exception to almost every statement. In late 1998 concern about the solvency of

some Japanese banks led to a large volume of yen deposits with Western banks. Some of these banks

charged their customers interest on these deposits; the nominal interest rate was negative.

real

money

⫽ .05 ⫹ .10 ⫹ .101.052⫽ .155

money

⫽ r

real

⫹ i ⫹ i1r

real

1 ⫹ r

money

⫽ 11 ⫹ r

real

2 11 ⫹ i2

1.10 ⫻ 105 ⫽ $115.50

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

was above. The average real interest rate during this period was a mere 0.1 percent.

Since 1981 the return on bills has been significantly higher than the rate of infla-

tion, so that investors have earned a positive real return on their savings.

Fisher’s theory states that changes in anticipated inflation produce correspon-

ding changes in the rate of interest. But Figure 24.2 offers little evidence of this in

the 1930s and 1940s. During this period, the return on Treasury bills scarcely

changed even though the inflation rate fluctuated sharply. Either these changes in

inflation were unanticipated or Fisher’s theory was wrong. Since the early 1950s,

there appears to have been a closer relationship between interest rates and infla-

tion in the United States.

Thus, for today’s financial managers Fisher’s theory pro-

vides a useful rule of thumb. If the expected inflation rate changes, it is a good bet

that there will be a corresponding change in the interest rate.

CHAPTER 24

Valuing Debt 671

1926

1931

1936

1941

1946

1951

1956

1961

1966

1971

1976

1981

1986

1991

1996

-15

-10

-5

Year

Percent

Inflation

Treasury bill return

FIGURE 24.2

The return on U.S. Treasury bills and

the rate of inflation, 1926–2000.

Source: Ibbotson Associates, Inc.,

Chicago, 2001.

This probably reflects government policy, which before 1951 stabilized nominal interest rates. The 1951

“accord” between the Treasury and the Federal Reserve System permitted more flexible nominal inter-

est rates after 1951.

24.2 TERM STRUCTURE AND YIELDS TO MATURITY

We turn now to the relationship between short- and long-term rates of interest.

Suppose that we have a simple loan that pays $1 at time 1. The present value of this

loan is

Thus we discount the cash flow at , the rate appropriate for a one-period loan.

This rate, which is fixed today, is often called today’s one-period spot rate.

If we have a loan that pays $1 at both time 1 and time 2, present value is

PV ⫽

1 ⫹ r

⫹

11 ⫹ r

PV ⫽

1 ⫹ r

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

Thus the first period’s cash flow is discounted at today’s one-period spot rate and

the second period’s flow is discounted at today’s two-period spot rate. The series

of spot rates , etc., is one way of expressing the term structure of interest rates.

Yield to Maturity

Rather than discounting each of the payments at a different rate of interest, we could

find a single rate of discount that would produce the same present value. Such a rate

is known as the yield to maturity, though it is in fact no more than our old acquain-

tance, the internal rate of return (IRR), masquerading under another name. If we call

the yield to maturity y, we can write the present value of the two-year loan as

All you need to calculate y is the price of a bond, its annual payment, and its ma-

turity. You can then rapidly work out the yield with the aid of a preprogrammed

calculator.

The yield to maturity is unambiguous and easy to calculate. It is also the stock-

in-trade of any bond dealer. By now, however, you should have learned to treat any

internal rate of return with suspicion.

The more closely we examine the yield to

maturity, the less informative it is seen to be. Here is an example.

Example. It is 2003. You are contemplating an investment in U.S. Treasury bonds

and come across the following quotations for two bonds:

PV ⫽

1 ⫹ y

⫹

11 ⫹ y2

, r

672 PART VII Debt Financing

See Section 5.3.

The quoted bond price is known as the flat (or clean) price. The price that the bond buyer pays (some-

times called the dirty price) is equal to the flat price plus the interest that the seller has already earned on

the bond since the last interest payment date. You need to use the flat price to calculate yields to maturity.

Yield to Maturity

Bond Price (IRR)

5s of ‘08 85.21% 8.78%

10s of ‘08 105.43 8.62

The phrase “5s of ‘08” refers to a bond maturing in 2008, paying annual interest of

5 percent of the bond’s face value. The interest payment is called the coupon payment.

In continental Europe coupons are usually paid annually; in the United States they

are usually paid every six months, so the 5s of ‘08 would pay 2.5 percent of face value

every six months. To simplify the arithmetic, we will pretend throughout this chap-

ter that all coupon payments are annual. When the bonds mature in 2008, bond-

holders receive the bond’s face value in addition to the final interest payment.

The price of each bond is quoted as a percent of face value. Therefore, if face

value is $1,000, you would have to pay $852.11 to buy the bond and your yield

would be 8.78 percent. Letting 2003 be , 2004 be , etc., we have the fol-

lowing discounted-cash-flow calculation:

t ⫽ 1t ⫽ 0

Cash Flows

Bond C

Yield

5s of ‘08 ⫺852.11 ⫹50 ⫹50 ⫹50 ⫹50 ⫹1,050 8.78%

10s of ‘08 ⫺1,054.29 ⫹100 ⫹100 ⫹100 ⫹100 ⫹1,100 8.62

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

Although the two bonds mature at the same date, they presumably were issued at

different times—the 5s when interest rates were low and the 10s when interest rates

were high.

Are the 5s of ‘08 a better buy? Is the market making a mistake by pricing these

two issues at different yields? The only way you will know for sure is to calculate

the bonds’ present values by using spot rates of interest: for 2004, for 2005, etc.

This is done in Table 24.1.

The important assumption in Table 24.1 is that long-term interest rates are

higher than short-term interest rates. We have assumed that the one-year interest

rate is , the two-year rate is , and so on. When each year’s cash flow

is discounted at the rate appropriate to that year, we see that each bond’s present

value is exactly equal to the quoted price. Thus each bond is fairly priced.

Why do the 5s have a higher yield? Because for each dollar that you invest in the

5s you receive relatively little cash inflow in the first four years and a relatively

high cash inflow in the final year. Therefore, although the two bonds have identi-

cal maturity dates, the 5s provide a greater proportion of their cash flows in 2008.

In this sense the 5s are a longer-term investment than the 10s. Their higher yield to

maturity just reflects the fact that long-term interest rates are higher than short-

term rates.

Notice why the yield to maturity can be misleading. When the yield is calculated,

the same rate is used to discount all payments on the bond. But in our example bond-

holders actually demanded different rates of return ( , etc.) for cash flows that oc-

curred at different times. Since the cash flows on the two bonds were not identical,

the bonds had different yields to maturity. Therefore, the yield to maturity on the 5s

of ‘08 offered only a rough guide to the appropriate yield on the 10s of ‘08.

Measuring the Term Structure

Financial managers who just want a quick, summary measure of interest rates look

in the financial press at the yields to maturity on government bonds. Thus managers

will make broad generalizations such as “If we borrow money today, we will have

to pay an interest rate of 8 percent.” But if you wish to understand why different

, r

⫽ .06r

⫽ .05

CHAPTER 24 Valuing Debt 673

Present Value Calculations

5s of ‘08 10s of ‘08

Interest

Period Rate C

PV at r

t ⫽ 1 r

⫽ .05 $ 50 $ 47.62 $ 100 $ 95.24

t ⫽ 2 r

⫽ .06 50 44.50 100 89.00

t ⫽ 3 r

⫽ .07 50 40.81 100 81.63

t ⫽ 4 r

⫽ .08 50 36.75 100 73.50

t ⫽ 5 r

⫽ .09 1,050 682.43 1,100 714.92

Totals $852.11 $1,054.29

TABLE 24.1

Calculating present value of two

bonds when long-term interest

rates are higher than short-term

rates.

For a good analysis of the relationship between the yield to maturity and spot interest rates, see S. M.

Schaefer, “The Problem with Redemption Yields,” Financial Analysts Journal 33 (July–August 1977),

pp. 59–67.